Explore topic-wise InterviewSolutions in Current Affairs.

This section includes 7 InterviewSolutions, each offering curated multiple-choice questions to sharpen your Current Affairs knowledge and support exam preparation. Choose a topic below to get started.

1.

A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical bottles of diameter 5 cm and height 6 cm How many bottles are necessary to empty the bowl ?

Answer»


ANSWER :60
Discussion
2.

For two circles of radii r and R, the distance between their centres is d. What type of circles are they, if d lt R +r?

Answer»


ANSWER :Non-intersecting CIRCLES
Discussion
3.

Fill in the blank using the correct word given in bracket : All circle are ................ .

Answer»


ANSWER :SIMILAR
Discussion
4.

The sum of first 7 terms of an A.P. is 49 and that of first 17 terms of it is 289. Find the sum of first n terms.

Answer»


ANSWER :`n^2`
Discussion
5.

From the following data, State whether Delta ABC is similar to Delta DEF or not : (a) /_ A = 70^(@), /_B = 80^(@), /_ D = 70^(@), /_ F= 30^(@) (b) AB = 8 cm, BC = 9 cm, CA = 15 cm, DE = 4 cm, EF = 3 cm, FD = 5 cm.

Answer»


ANSWER :`(BC)/(EF)`
Discussion
6.

If in a certain language, NEOMAN is coded as OGRQFT, which word will be coded as ZKCLUP?

Answer»

YJBKTO
XIAJSN
YIZHPJ
YIAQKJ

Solution :CLEARLY the letters in the word are 1,2,3,4,5 and 6 PLACES before the CORRESPONDING alphaets in the given code
Discussion
7.

Find the remainder when x^(2)-8x+4 is divided by 2x+1.

Answer»


ANSWER :`8 1/4`
Discussion
8.

Angles inscribed in the same arc are

Answer»

congruent
complementary
supplementary
none of these

Answer :A
Discussion
9.

The median of the following data is 525. find the the value of x and y, if the total frequency is 100 :

Answer»


ANSWER :X = 9, y = 15
Discussion
10.

Find the area of the trianglevertices are (0, 0), (3, 0) and (0, 2)

Answer»


ANSWER :3 SQ. UNITS
Discussion
11.

Is the adjoining figure, the value of theta is

Answer»

`30^(@)`
`45^(@)`
`60^(@)`
`75^(@)`

Solution :The given FIGURE is a right-angled triangle of which of length of PERPENDICULAR is 5 metres and the length of base is `5sqrt(3)` METERS.
`therefore"" tan theta =(5"metres")/(5sqrt(3)"metres")` [by DEFINITION ]
or, `tan theta =(1)/(sqrt(3)) = tan30^(@) ""rArr "" theta =30^(@)`
Hence (a) is correct.
Discussion
12.

A vessel isa hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is (14)/3m and thediameter of hemisphere is 3.5 m. Calculate the volume and the internalsurface area of the solid.

Answer»


ANSWER :`56.15 m ^(3) and 70.58 m ^(2)`
Discussion
13.

Find the sum of first 51 terms of an A.P. whose second and thrid are 14 and 18 respectively.

Answer»


ANSWER :5TH TERM
Discussion
14.

How many rectangles does the following figure have ?

Answer»

10
12
13
14

Answer :D
Discussion
15.

A clock is so placed that at 12 noon its minute hand points towards North-east. In which direction does its hour point at 1:30 p.m.

Answer»

North
South
EAST
West

Solution :Diagram is shown as PER the conditions in the question. CLEARLY at 1:30 p.m. the hour hand SHALL POINT East.
Discussion
16.

Evaluate: (i) 3[(5),(-2)] (ii) 7 [{:(,-1,2),(,0,1):}] (iii) 2[{:(,-1, 0),(,2,-3):}] +[{:(,3,3),(,5,0):}]

Answer»


Answer :(i) [15-6] (II) `[{:(,-7,14),(,0,7):}]` (iii) `[{:(,1,3),(,9,-6):}]` (iv) `[{:(,34),(,14):}]`
Discussion
17.

Find the roots of the equation 2x^(2)-5x+3=0, by factorisation.

Answer»


ANSWER :`1 and (3)/(2)`
Discussion
18.

Refer to 0.4 above. Draw the less then type ogive for this data and use it to find the median weight.

Answer»

Solution :We observe that the number of packets less than 200 is 0. Similarly, less than 201 includes the number of pacakets from 0-200 as well as the number of packets from 200-201. So, the total number of packets less than 201 is 0+13=12. We SAY that , the cumulative FREQUENCY of the class 200-201 is 13. Similarly for other class.

To draw the less than type OGIVE we plot the points (200,0), (201,13),(202,40),(203,58),(204,68),(205,69) and (206,70) on the paper and join by free hand.
`therefore` Total number of packets(n)=70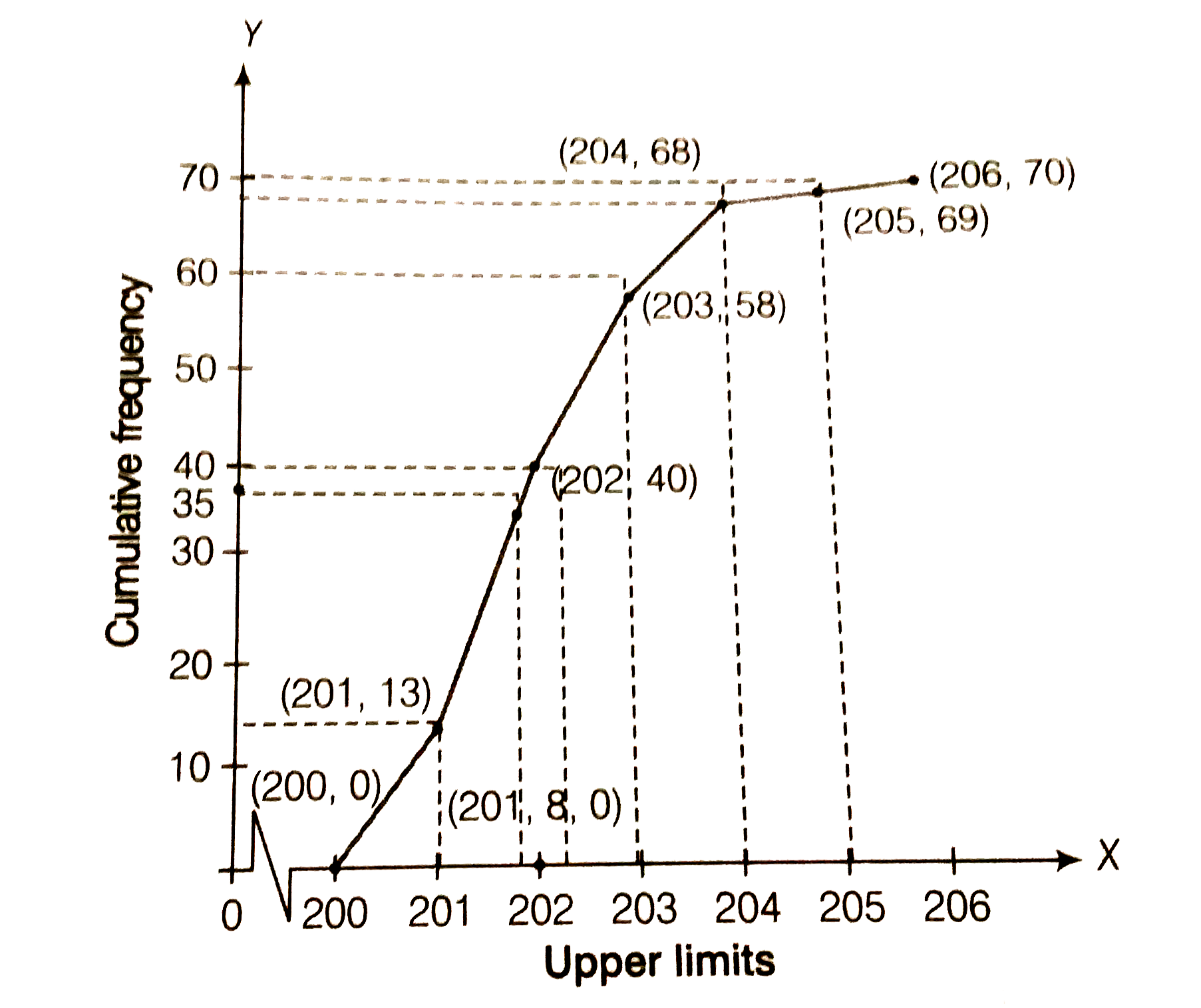

Now, Firstly, we plot a point (0,35) on Y-axis and draw a LINE =35 parallel to X-axis. The line cuts the less than ogive curve at a point. We draw a line on that point which is PERPENDICULAR to x-axis. The foot of hte perpendicular to X-axis is the required meidan.
`therefore` Median weight=201.8g
Discussion
19.

Show that the points (-2, 1) (2, -2) and (5, -2) are the vertices of a right angled triangle.

Answer»


Answer :`:.DELTAABC` is a RIGHT ANGLED triangled at B.
Discussion
20.

A frustum of a cone whose slant height is 10 cm has diameters of ends as 32 cm and 20 cm. then its capacity is

Answer»


ANSWER :C
Discussion
21.

If 1 is subtracted from the numerator and 2 is added to the denomenator of a fraction it becomes (1)/(2), also, if 7 is subtracted from the numberator and 2 is subtracted from the denominator then the fraction becomes (1)/(3). Find the fraction.

Answer»


ANSWER :`(15)/(26)`;
Discussion
22.

Draw a cirle with centre P. Draw an are AB of 100^@ measure Draw tangent to the circle at point A and B

Answer»

SOLUTION :
Analsis :
`m ("arc AB")=100^@""...("Given")`
`angleAPB=m("arc AB")""...("Defnition of measure of minor arc")`
`thereforeangleAPB=100^@`
Central `angleAPB` can be DRAWN in the CIRCLE and thus points A and B can be located on the circle. Tangents at A and B can thus be constructed
Construction :
Discussion
23.

Three identical coins are tossed together. What is the probability of obtaining : at least two heads ?

Answer»


ANSWER :`1/2`
Discussion
24.

Identify the polynomialsfrom the 10 algebraic equations given above. Give reason why some of them are not polynomials.

Answer»


Answer :9 is NOTA polynomial as `X^(-2)` isnegative POWER of x.
Discussion
25.

Which one of the following sets is best represented in the adjoining diagram?

Answer»

Animals,Insects,Cockroaches
Country,States,DISTRICTS
Animals,MALES,FEMALES and Hermaphrodites
States,Districts,UNION Territory

Solution :District form PART of the state.But Union Territory is entirely different.
Discussion
26.

Represent the following situations in the form of quadratic equation: A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train

Answer»


ANSWER :`X^(2)-8x-1280=0`(x=Speed of the TRAIN)
Discussion
27.

For unique solution of the equations x-2y-3= and 3x+ky-1=0, the value of k is :

Answer»

`K NE 6`
`k ne3`
`k ne -6`
None of these

Answer :C
Discussion
28.

A solid metallic ball is dropped in a cylindrical vessel which has some waater .when this ball is fully immersed in water the water surface rises by 2 cm find the volume of ball if the radius of base of cylindrical vessel is 7cm.

Answer»


ANSWER :77 `CM^(3)`
Discussion
29.

The sum of three numbers in G.P. is (39)/(10) and their product is 1. Find the numbers.

Answer»


ANSWER :`(2)/(5)`, 1 and `(5)/(2)` or `(5)/(2),1" and "(2)/(5)`
Discussion
30.

The value of diamond varies as the square of their weights and the squqre of the values of rubbies varies as the cube of their weight . A diamond of 'a' carats is worth m times the value of ruby of 'b'carats and both together worth 'c' rupees . Find the values of a diamond and of a ruby each weighing 'n' carats.

Answer»
Discussion
31.

The table below shows daily expenditure on food of 25 households in a locality. Find the mean daily expenditure.

Answer»


ANSWER :`VEC(X)` = 211
Discussion
32.

If A=[{:(,2,x),(,0,1):}] and B=[{:(,4,36),(,0,1):}], find the value of x, given that A^2=B

Answer»


ANSWER :x=12
Discussion
33.

A letter is chosen at random from the letter of the word "PROBABILITY". Find the probability that isnot a vowel.

Answer»

`(1)/(5)`
`(2)/(5)`
`(1)/(3)`
`(3)/(5)`

Answer :B
Discussion
34.

Evaluate : (sec theta ."cosec" (90^(@) - theta) - tan theta.cot (90^(@) - theta) + sin^(2) 55^(@) + sin^(2) 35^(@))/(tan 10^(@).tan 20^(@).tan 60^(@).tan 70^(@).tan 80^(@))

Answer»


ANSWER :`(2 SQRT(3))/(3)` .
Discussion
35.

Choose the correct answer and give justification for each. If AP and AQ are the two tangents a circle with centre O so that /_POQ=110^(@), then /_PAQ is equal to

Answer»

`60^(@)`
`70^(@)`
`80^(@)`
`90^(@)`

ANSWER :B
Discussion
36.

A point P (a, b) is reflected in the x-axis to P'(2, -3). Write down the values of a and b. P" is the image of P, reflected in the y-axis. Write down the co-ordinates of P". Find the co-ordinates of P", when P is reflected in the line, parallel to y-axis, such that x = 4.

Answer»

<P>

ANSWER :a = 2 , B = 3 P'' = (-2,3), P''' = (6,3)
Discussion
37.

A solid spherical ball of iron with radius 6 cm is melted and recast into three solid spherical balls. The radii of the two balls are 3 cm and 4 cm respectively, determine the diameter of the third ball.

Answer»


ANSWER :10 CM
Discussion
38.

Write the following expressions as log N and find their values. log 10 + 2 log 3 - log 2

Answer»


ANSWER :LOG45
Discussion
39.

A ladder 17 m long reaches a window of a building 15 m above the ground. The distance of the foot of the ladder from the building is?

Answer»


ANSWER :8 m
Discussion
40.

PQR is a triangle with PQ=10cm, QR=8cm and PR=11cm. Three circles are drawn touching with each other such that the vertices as their centres. Find the radii of each circle.

Answer»


ANSWER :4.5 CM
Discussion
41.

A solid cyclinderhas diameter 28 cmand height 24 cm . A conical cavity of the same diameter and the same height is drilled out fromthis solid. Find the whole surfacesaea of remaining solid.

Answer»


ANSWER :` 3950 .32 CM ^(2)`
Discussion
42.

Angles made by the line with the positive direction of X-axis are given . Find the slope of these lines . (iii)90^@

Answer»


ANSWER :`THEREFORE` The SLOPE of the LINE cannot be DETERMINED.
Discussion
43.

Verify whether the points (1, 5), (2, 3) and (-2, -1) are collinear or not.

Answer»


Answer :POINTS are not collinear 4. AB = BC = `SQRT(37)`; AC = 2
Discussion
44.

Find the radius of a circle whose circumference is equal to the sum of the circumference of two circles of diameter 36 cm and 20 cm.

Answer»


ANSWER :28 CM
Discussion
45.

Solve the following equation : 3^(x+2)+3^(-x)=10

Answer»

SOLUTION :Given equation is
`3^(X+2)+3^(-x)=10`
`implies3^(x)xx3^(2)+(1)/(3^(x))=10implies9xx3^(x)+(1)/(3^(x))=10"".....(2)`
LET `3^(x)=a``3^(x)=a""......(2)`
Then from (1)
`9a+(1)/(a)=10`
`implies9a^(2)+1=10a ""implies9a^(2)-10a+1=0`
`implies9a^(2)-(9+1)a+1=0""implies9a^(2)-9a-a+1=0`
`implies9a(a-1)-1(a-1)=0""implies(9a-1)(a-1)=0`
`implies9a-1=0""or""a-1=0`
when `9a-1=0impliesa=(1)/(9)`
and when `a-1=0impliesa=1`
Substituting values of a in equation (2)
when `a=(1)/(9)`
`3^(x)=(1)/(9)""implies""3^(x)=(1)/(3^(2)`
`implies3^(x)=3^(-2)""or""x=-2`
when a=1
`3^(x)=1`
`implies3^(x)=3^(0)""implies""x=0`
HENCE, 0 and -2 are roots of the equation.
Discussion
46.

Sachin invested in a National Saving Certificate scheme. In the 1^(th) year, he invested ₹5000, in 2^(nd) year ₹7000, in 3^(rd) year ₹9000 and so on. Find the total amount that he invested in 12 years.

Answer»


ANSWER :`THEREFORE`Total investment DONE in 12 years is ₹1,92,000
Discussion
47.

Pointing to an old man,Sohan said, "His son is my son's uncle." How is old man related to Sohan?

Answer»

BROTHER
Uncle
Father
Grand father

SOLUTION :SOHAN.s son,s uncle means Sohan.s brother .So, the OLD man.s son is Sohan .s brother ,i.e. the old man is the father of Sohan.The answer is (c ).
Discussion
48.

A container shaped like a right circular cylinder having diameter 12 cm. and height 15 cm. is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm. and diameter 6 cm., having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.

Answer»


ANSWER :10
Discussion
49.

Two line segment AB and AC include an angle of 60^(@), where AB=5 cm and AC= 7 cm. Locate points P and Q on AB and AC, respectively such that AP=(3)/(4)AB and AQ=(1)/(4)AC. Join P and Q and measure the length PQ.

Answer»

Solution :Given that ,AB= 5 cm and AC= 7 cm.
Also,`AP=(3)/(4)AB` and `AQ=(1)/(4)AC` …..(i)
From Eq. (i), `AP=(3)/(4).AB=(3)/(4)xx5=(15)/(4)cm`
Then, `PB=AB-AP=5-(15)/(4)=(20-15)/(4)=(5)/(4) cm` [ `:.` P is any point on the AB]
`:. AP:PB=(15)/(4):(5)/(4)implies AP:PB=3:1`
i.e, scale factor of line segment AB is `(3)/(1)`.
Again from Eq. (i), `AQ=(1)/(4)AC=(1)/(4)xx7=(7)/(4)cm`
Then, `QC=AC-AQ=7-(1)/(4)`
`=(28-7)/(4)=(21)/(4) cm` [`:.` Q is any point on the AC]

`:. AQ:QC=(7)/(4):(21)/(4)=1:3`
`implies AQ:QC =1:3`
i.e., scale factor of line segment AQ is `(1)/(3)`.
Steps of construction
1. Draw a line segment AB=5 cm.
2. Now draw a ray AZ making an acute `angleBAZ=60^(@)`.
3. Whit A as centre and radius EQUAL to 7 cm draw an arc CUTTING the line AZ at C.
4. Draw a ray AX, making an acute ` angle BAX`.
5. Along AX , mark 1+3=4 points `A_(1),A_(2),A_(3), " and " A_(4)`.
Such that `A A_(1)=A_(1)A_(2)=A_(2)A_(3)=A_(3)A_(4)`
6. Join `A_(4)B` ltbr. 7. From `A_(3)` draw `A_(3)P||A_(4)B` meeting AB at P. [ by making an angle equal to `angleAA_(4)B`]
Then, P is the point on AB which DIVIDED it in the ratio 3:1.
So, AP:PB=3:1 ,brgt 8. Draw a ray AY, making an acute `angleCAY`.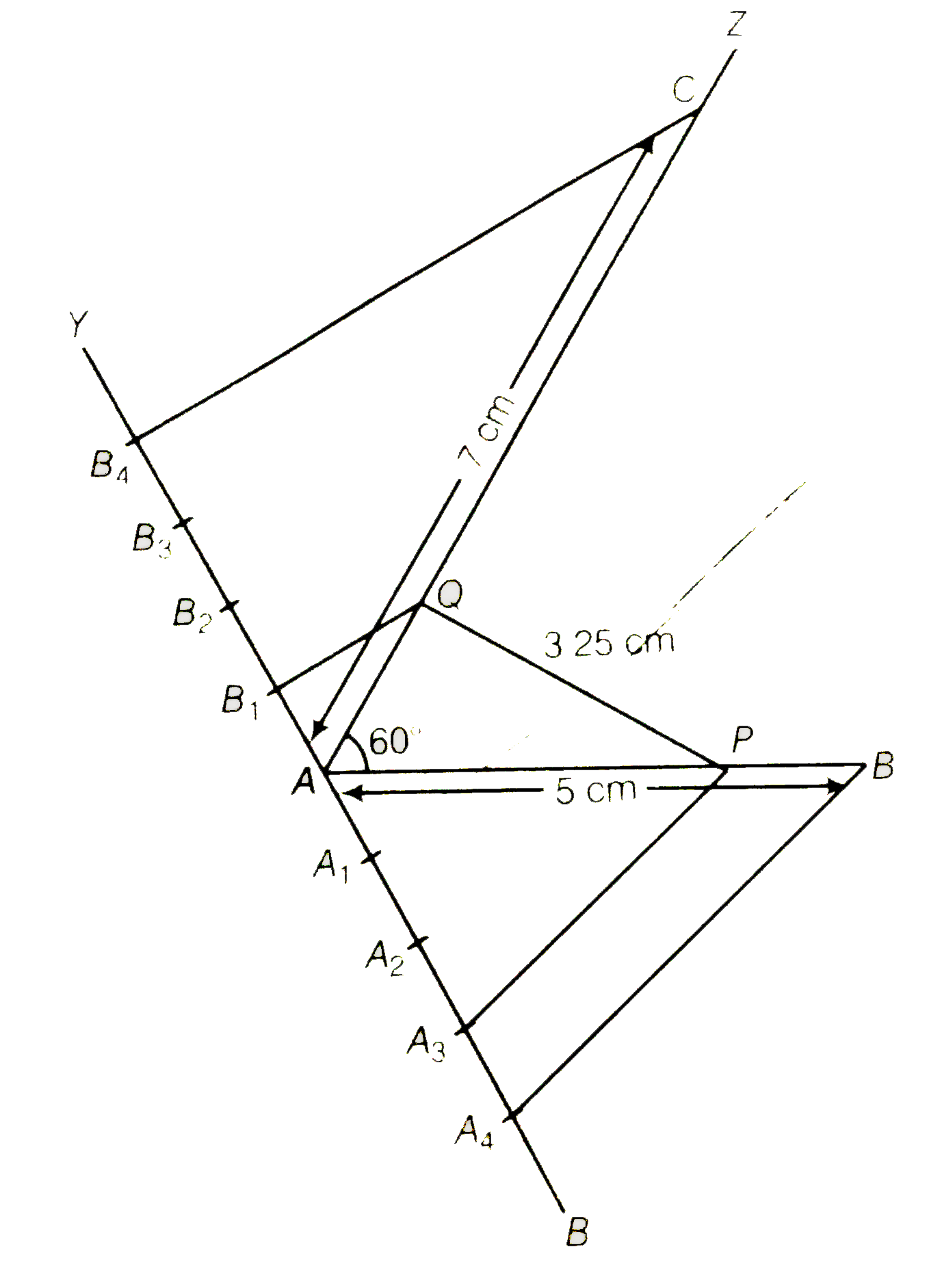

9. Along AY, mark 3+1=4 points `B_(1),B_(2),B_(3) " and " B_(4)`
Such that `AB_(1)=B_(1)B_(2)=B_(2)B_(3)=B_(3)B_(4)`
10. Join `B_(4)C`.
11. From `B_(1)` draw `B_(1)Q||B_(4)C` meeting AC at Q. [by making an angle equal to `angleAB_(4)C`]
Then, Q is the point on AC which divides in the ratio 1:3.
So, AQ:QC=1:3 ltbtgt 12. Finally, join PQ and its MEASUREMENT is 3.25 cm.
Discussion
50.

Two water taps together can fill a tank in 9 3/8 hrs. The tap of the larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

Answer»


ANSWER :`=25 H`
Discussion