InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1851. |
If alphaand beta are zeros of polynomial 6x^(2)-7x-3, then form a quadratic polynomial where zeros are 2alpha and 2beta |
|
Answer» |
|
| 1852. |
How many spherical lead shots each of diameter height 24 cm is full of water. The water is emptied into a cylinderical vessel with internal radius 10 cm. find the height of the water in the cylinderical vessel. |
|
Answer» |
|
| 1853. |
If thetotal surface area of a cylindrical pot open at one end is 1474 sq-cm . Then the height of the pot is equal to _______ cm. |
|
Answer» |
|
| 1854. |
A 15 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30^@ to 60^@ as the walls towards the building. Find the distance he walked towards the building. |
|
Answer» |
|
| 1855. |
Find the sums given below : (i) 7+10(1)/(2)+14+……..+84 (ii) 34+32+30+…..+10 (iii) -5+(-8)+(-11)+………+(-230) |
|
Answer» |
|
| 1856. |
If x=a+b, y= b+c , z=c+a, then the value of (x^(3) + y^(3) + z^(3) - 3xyz)/( a^(3) + b^(3) + c^(3) -3 abc) is equal to |
| Answer» ANSWER :B | |
| 1857. |
For what value of K, the pair of equations 2x + ky = 1, 3x - 5y = 7 has a unique solution? |
|
Answer» `K = (-10)/3` |
|
| 1859. |
Split 207 into three parts such that these parts are in A.P. and the product of the two smaller parts is 4623. |
|
Answer» |
|
| 1860. |
During the medical checkup of 35 students of a class their weight were recorded as follows : Draw a less than type a more than type ogive from the given data. Hene obtain the median weigth from the graph. |
|
Answer» Solution : (i) Less than SERIES : We may prepare the less than series as under:  `"Scale":{{:("Along the X-axis,5 small div.",=1kg),("Along the Y-axis, 10 small div.",=5KG):}` We plot the points A(40,3),B(42,5),C(44,9),D(46,14),E(48,28),F(50,32) and G(52,35) . Join AB, BC, CD, EF, and FG with a FREE hand ot GET the cruve repressentingLess than series. (ii) More than Series : We many prepare the more series as under : 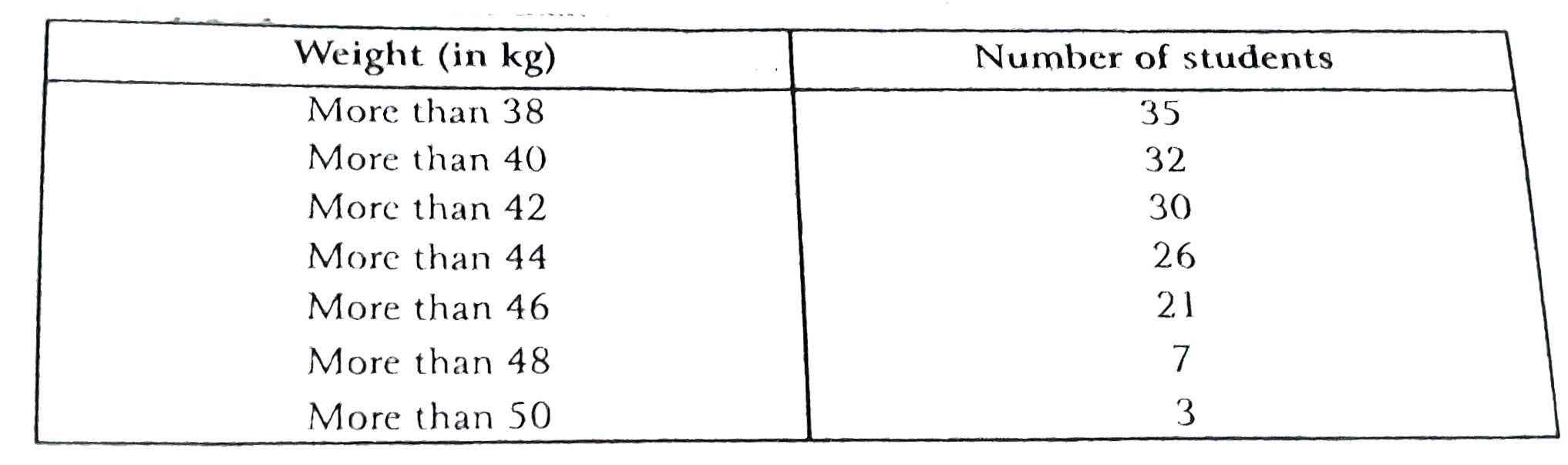 On the same grph-paper as above we plot the points P(38,35),Q(40,32), R(42,30), S(44,26),T(46,21), U (48,7) and V(50,3), . Join PQ,QR,RS, ST,TU,jand UV, with a free hadn to get cruve represnting 'More than sereis' `"Scale":{{:("Along the X-axis,5 small div.",=1kg),("Along the Y-axis, 10 small div.",=5"student"):}` 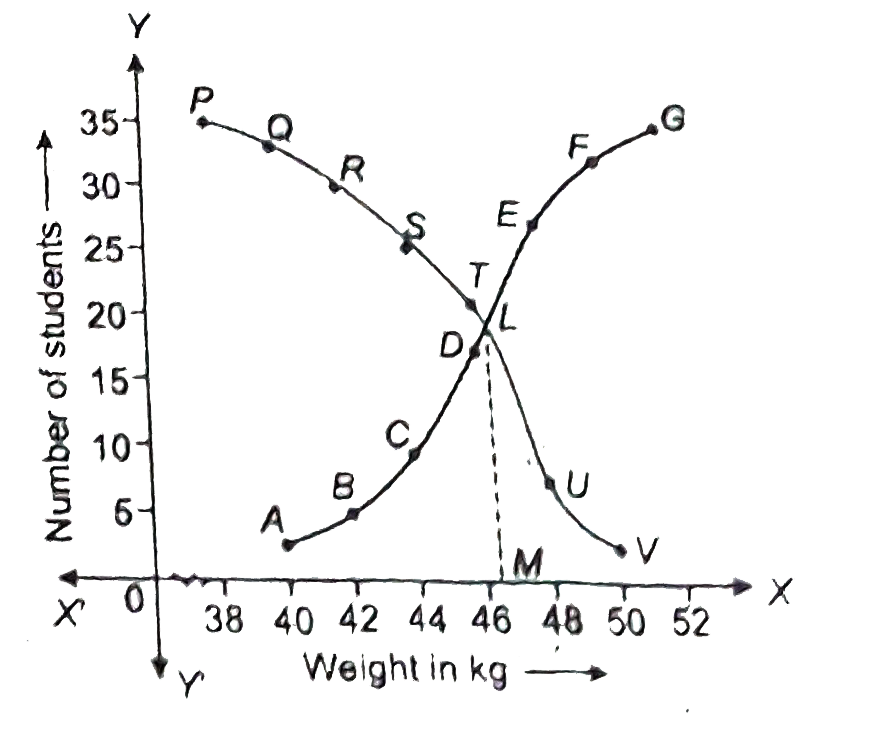 The two cruves intersect at tht point L. Draw `LMbotOX` `:.` Median weight = OM =46.5 kg |
|
| 1861. |
( 2tan 30 ^(@) )/( 1+tan ^(2) 45^(@) ) = |
|
Answer» `SIN 60^(@) ` |
|
| 1862. |
The table below gives the percentage distribution of female teachers in the schools of rural areas. Find the mean percentage of female teachers. |
|
Answer» |
|
| 1863. |
Solved the equation by using quadratic formula a(x^(2)+1)=(a^(2)+1)x,ane0. |
|
Answer» SOLUTION :GIVEN equation is `a(x^(2)+1)=(a^(2)+1)x` `impliesax^(2)+a=a^(2)x+x` `impliesax^(2)-x(a^(2)+1)+a=0` COMPARING with `Ax^(2)+Bx+C=0`, we get `A=a,B=-(a^(2)+1)andC=a` `:.x=(-B+-sqrt(B^(2)-4AC))/(2A)` `impliesx=(-[-(a^(2)+1)]+-sqrt({-(a^(2)+1)}^(2)-4xxaxxa))/(2a)` `impliesx=((a^(2)+1)+-sqrt(a^(4)+1+2a^(2)-4a^(2)))/(2a)` `impliesx=((a^(2)+1)+-sqrt((a^(2)-1))^(2))/(2a)` `impliesx=((a^(2)+1)+-(a^(2)-1))/(2a)` `impliesx=(a^(2)+1+a^(2)-1)/(2a)and(a^(2)+1-a^(2)+1)/(2a)` `impliesx=(2a^(2))/(2a)and(2)/(2a)` `impliesx=aand(1)/(a)` are ROOTS of the equation. |
|
| 1864. |
Solve the following pair of equations by reducing them to a pair of linear equations : (10)/(x+y)+(2)/(x-y)=4 and (15)/(x+y)-(5)/(x-y)=-2. |
|
Answer» |
|
| 1865. |
Find the maximum value of 4x+7y with theconditions 3x+8y le 24, y le2,x ge 0, and y ge 0. |
|
Answer» 14 `y le 2, x gt 0, y GE 0`. 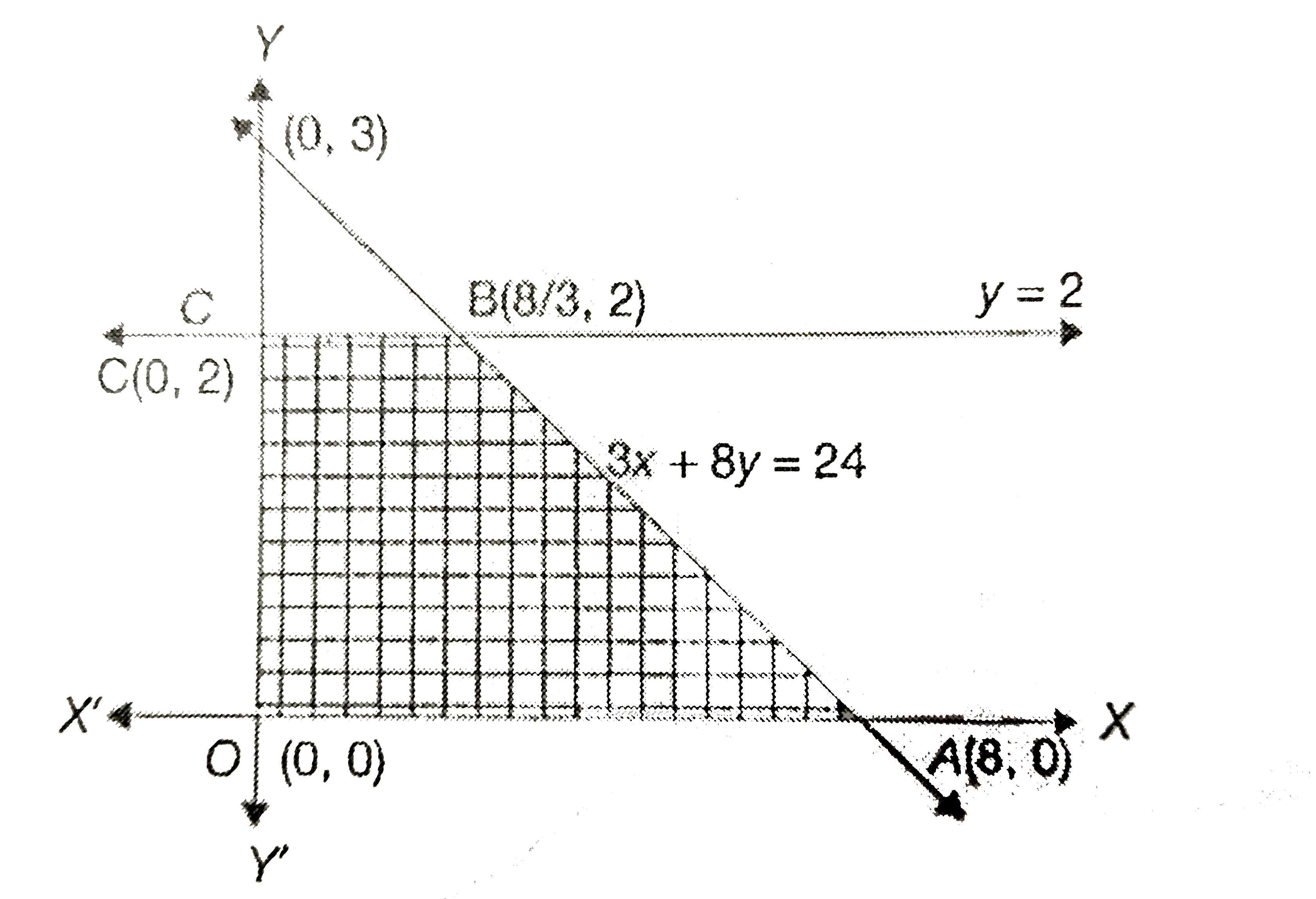 The vertices of the feasible polygon region are (0,0), (8,0),(8/3,2) nad (0,3). The MAXIMUM value of the objective function attains at (8,0). f=4x+7y The maximum value `=4xx8+7xx0=32` |
|
| 1866. |
Write the following rationals in decimal form using 7218/(3^(3).5^2) |
|
Answer» |
|
| 1867. |
If cotalpha+tanalpha=mand(1)/(cosalpha)-cosalpha=n, then show thatm(mn^(2))^(1//3)-n(nm^(2))^(1//3)=1. |
| Answer» | |
| 1868. |
If A={1,2,3,4} and B={1,2,3,5,6}, then find A cap B and B cap A. Are they equal. |
|
Answer» |
|
| 1869. |
A construction company will be penalised each day for delay in construction of a bridge. The penalty will be Rs 4000 for the first day and will increase byRs 1000 for each following day. Based on its budget, the company can afford to pay a maximum ofRs 1,65,000 towards penalty. Find the maximum number of days by which the construction of work can be delayed. |
|
Answer» |
|
| 1870. |
A person, invested some amount at the rate of 12% simple interest and some other amount at the rate of 10% simple interest. He received yearly interest of Rs. 130. But if he had interchanged the amount invested, he would have received Rs. 4 more as interest. How much did he invest at different rates? |
|
Answer» |
|
| 1871. |
A person invests Rs. 15,000 in Rs. 50 shares of a company paying 10% dividend. If the company pays a dividend of Rs. 6250, the market value of each share is ___________. |
|
Answer» Rs. 8 (II) By using the FOLLOWING formula find `MV`. Use, `FVxx` Rate of dividend `=MVxx` Rate of return. |
|
| 1872. |
In two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously. What is the probability of getting the sum of atleast 10? |
|
Answer» `(5)/(12)` Thus number of favourable outcomes, `N(E_(3))=6` P(sum of atleast 10), `P(E_(3))=(n(E_(3)))/(n(S))=(6)/(36)=(1)/(6))` Thus ( c ) is correct option. |
|
| 1873. |
In two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously. What is the probability of getting a doublet of even number ? |
|
Answer» <P>`(1)/(12)` Thus number of favourable outcomes, `N(E_(3))=3` P(doublet of even number), `P(E_(4))=(n(E_(4)))/(n(S))=(3)/(36)=(1)/(12)` Thus ( c ) is correct OPTION. |
|
| 1874. |
In two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously. What is the probability of getting a product of numbers greater than 16? |
|
Answer» <P>`(7)/(36)` THUS number of favourable outcomes, `n(E_(5))=7` P(product of numbers greater than 16), `P(E_(5))=(n(E_(5)))/(n(S))=(7)/(36)` Thus ( c ) is correct option. |
|
| 1875. |
In two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously. What is the probability of getting the sum as a prime number ? |
|
Answer» `(5)/(12)` `{1(1, 1), (1, 2), (2, 1), (1, 4), (4, 1), (2, 3), (3, 2), (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3), (6, 5), (5, 6)}` Thus number of favourable OUTCOMES, `n(E_(1))=15` P(sum as a prime number), `P(E_(2))=(n(E_(2)))/(n(S))=(15)/(36)=(5)/(12)` Thus (a) is correct option. |
|
| 1876. |
In two dice game, the player take turns to roll both dice, they can roll as many times as they want in one turn. A player scores the sum of the two dice thrown and gradually reaches a higher score as they continue to roll. If a single number 1 is thrown on either die, the score for that whole turn is lost. Two dice are thrown simultaneously. What is the probability of getting the sum as an even number ? |
|
Answer» `(3)/(4)` (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6) (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) NUMBER of all possible outcomes in all case, `n(S)=6xx6=36` Favourable outcome are {2, 4, 6, 8, 10, 12}. We may get as follows `{(1, 1), (1, 3), (3, 1), (2, 2), (1, 5), (5, 1), (2, 4), (4, 2), (3, 3), (2, 6), (6, 2), (3, 5), (5, 3), (4, 4), (6, 4), (4, 6), (5, 5), (6, 6)}` Thus number of favourable outcomes, `n(E_(1))=18` P(sum as an even number), `P(E_(1))=(n(E_(1)))/(n(S))=(18)/(36)=(1)/(2)` Thus (d) is correct option. |
|
| 1877. |
Using a graph paper, plot the points A (6, 4)and B(0, 4). State the geometrical name for the figure ABA'B'. |
|
Answer» |
|
| 1878. |
Find the nature of the roots of the quadratic equations. If real roots exist, find them 2x^(2)-6x+3=0 |
|
Answer» |
|
| 1879. |
What is the value of (sin (30^@-A))/(cos A-sqrt3sin A) |
|
Answer» |
|
| 1881. |
Find the A.P. whose nth term is 2n-3. |
|
Answer» |
|
| 1882. |
A child is looking for his father. He went 90 metres in the east before turning to hits right. He went 20 metres before turning to his right again to look for his father at his uncle's place 30 metres from this point. His father was not presence there. From there, he went 100 metres to his North before meeting his father in a street. How far did the son meet his father from starting point ? |
|
Answer» AB = 90M, BC = 20M, CD = 30 m. DL = 20m, DE = 100 m and EL = 80 m. AL = 60 m  `:. AE = sqrt(AL^(2) + LE^(2)) = sqrt(60 + 80^(2))` `= sqrt(10, 000) = 100 m` |
|
| 1883. |
How many numbers are amongst the numbers 9 to 54 are there which are exactly divisible by 9 but by 3? |
|
Answer» 8 |
|
| 1884. |
Draw a circle of radius 5 cm. From a point P, 8 cm away from its centre, construct a pair of tangents to the circle. Measure the length of each one of the tangents. |
|
Answer» |
|
| 1885. |
If the points (1, x), (5, 2) and (9, 5) are collinear then find the value of x. |
|
Answer» |
|
| 1886. |
Find the value of p, if x, 2x + p and 3x + 6 are in A.P. |
|
Answer» |
|
| 1887. |
If the sum of the first q terms of an AP is 2q + 3q^(2), what is its common difference? |
|
Answer» |
|
| 1888. |
Find the zeroes of the polynomial f(y)=y^(3)-5y^(2)-2y+24, if it is given that the product of its two zeroes is 12. |
|
Answer» |
|
| 1889. |
If sec((pi)/(2)-alpha)+cosec((pi)/(2)-alpha). |
|
Answer» Solution :`sec((pi)/(2)-alpha)+COSEC((pi)/(2)-alpha)` `=cosecalpha+secalpha=(1)/(SINALPHA)+(1)/(COSALPHA)=(cosalpha+sinalpha)/(sinalphacosalpha)` `=(sinalpha+sinalpha)/(sinalphasinalpha)[:'sinalpha-cosalpha=0impliessinalphacosalpha]` Again, `sinalpha=cosalpha=sin(90^(@)-alpha)` `impliesalpha=90^(@)-alphaor,2alpha=90^(@)or,alpha=(90^(@))/(2)=45^(@)` `:.(sinalpha+sinalpha)/(sinalpha.sinalpha)=(2sinalpha)/(sin^(2)alpha)=(2)/(sinalpha)=(2)/(sin45^(@))=(2)/((1)/(sqrt2))=2sqrt2`. Hence `sec((pi)/(2)-alpha)+cosec((pi)/(2)-alpha)=2sqrt2`. |
|
| 1890. |
bar(AB) is a tangent drawn to a circle with centre O from an external point A ans B is a point of contact , then wich of the following is always true ? (i) OAgtOBOAgtAB(iii) ABgtOB |
|
Answer» only (i) |
|
| 1891. |
Area of the base a cone is 300 sq.Cm andheight is 15, then the volume is : |
| Answer» Answer :d | |
| 1892. |
Given that sqrt(3) is a zero of the polynomial x^3 + x^2 – 3x - 3, find its other two zeros. |
|
Answer» |
|
| 1893. |
If the areas of two similar triangles are equal, prove that they are congruent. |
|
Answer» |
|
| 1894. |
Find a point which is equidistant from the points A(-5,4)andB(-1,6) How many such points are there ? |
|
Answer» Solution :LET P (X,y) be the required point. Given that, `"" PA-PB` `implies""PA^(2)=PB^(2)` `implies""(x+5)^(2)+(y-4)^(2)=(x+1)^(2)+(y-6)^(2)` `implies""x^(2)+10x+25+y^(2)-8y+16=x^(2)+2x+1+y^(2)-12y+36` `implies""8x+4y+4=0` `implies""2x+y+1=0` It shows that INFINITE points are equidistant from AB because all points on perpendicular bisector of AB will be equidistant from AB. ONE such point is the mid-point of AB. which is `((-5-1)/(2),(4+6)/(2))=(-3,5)` |
|
| 1895. |
From a point P, two tangents PA and PB are drawn such that PA=9 cm and angleAPB=60^(@). Find the length of chord AB. |
|
Answer» |
|
| 1896. |
If in equation a_(1)x+b_(1)y+c_(1)=0 and a_(2)x+b_(2)y+c_(2)=0 are such that (a_(1))/(a_(2))ne(b_(1))/(b_(2)), then which of the following is true? |
|
Answer» No solution |
|
| 1897. |
Using the Remainder Theorem, factorise the expression3x^3+ 10x^2+ x- 6.Hence, solve the equation3x^3+ 10x^2+ x- 6=0. |
|
Answer» |
|
| 1898. |
Find the mean for the following distribution table by short cut method: |
Answer» Solution : Let ASSUMED MEAN a=35 ` "mean"barx=a+(sumf_(i)x_(i))/(sumf_(i))=35+(160)/(50)=35+3.2=38.2` |
|
| 1899. |
If A=[{:(,4,2),(,1,1):}], find (A-2I) (A-3I). |
|
Answer» |
|
| 1900. |
The product of four consectuive positive integers is 1680. find the numbers. |
|
Answer» |
|