InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1951. |
A man buys 75rs shares at a discount of 15rs of a company paying 20% dividend Find. (i) the market value of 120 shares (ii) his annual income (iii) his profit percent |
|
Answer» |
|
| 1952. |
A man wants to buy124 shares available at rupes 66 (par value = rupes 50 ) (i) How much shouldhe invest? (ii)if the divided is 7.5 %what will be his annual income? (iii)If he wantsto increase income by rupes 600. how many extra shares should he buy ? |
|
Answer» |
|
| 1953. |
The sum of four consecutive terms which are in an arithmetic progression is 32 and the ratio of the product of the first and the last term to the product to two middle terms is 7:15. Find the number. |
|
Answer» |
|
| 1954. |
If the vertices of a triangle are (2, 4), (5, k) and (3, 10) and its area is 15 sq. units, the value of k is |
| Answer» ANSWER :C | |
| 1955. |
In triangle ABC, angleBAC = 90^@, AB = 6cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e., an incircle ofDeltaABCis drawn).Find the area of the triangle excluding the circle. |
|
Answer» |
|
| 1956. |
A quadrilateralABCDis drawnto circumscribea circleasshown. Provethat AB+CD = AD +BC |
|
Answer» |
|
| 1957. |
Find the value of 'm'. If mx^3+ 2x^2- 3 and x^2- mx+ 4 leave the same remainder when each is divided by x- 2. |
|
Answer» |
|
| 1958. |
Sachin invests Rs. 8,500 in 10%,Rs. 100 shares at Rs. 170. He sells the shares whenthe price of each share rises by Rs. 30. He invests the proceeds in 12% Rs. 100 shares at 125. Find : (i) the scale proceeds. (ii) the number of Rs. 125 shares he buys. (iii) the change in his annual income. |
|
Answer» |
|
| 1959. |
Find the matrix A, if B=[{:(,2,1),(,0,1):}] and B^2=B+1/2A. |
|
Answer» |
|
| 1960. |
Let ABC be a right-triangle in which AB = 6 cm, BC = 8 cm , and B= 90^@. BD is the perpendicular from B on AC. A circle through B, C, D is drawn. Construct the tangent from A to this circle. |
|
Answer» |
|
| 1961. |
Referring to Figure 3.15, which could be the value of s when g(s)=0? I.-6 II.2 II.4 |
|
Answer» I only |
|
| 1962. |
Aftab tells his daughter "Seven years ago I was seven times as old were then. Also, three years from now, I shall be three times as old as you will be". Represent the situation algebraically and graphically. |
|
Answer» |
|
| 1963. |
Ashwarya bought 496, 100rs shares at 132rs each. Find (i) investment made by her (ii) income of Ashwarya from these shares, if the rate of dividend is 7.5% (iii) how much extra must Ashwarya invest in order to increase her income by 7200rs ? |
|
Answer» |
|
| 1964. |
Show that the following system of equations have unique solution :{:((i),7x-2y=3,(ii),3x+y=17,(iii),2x+5y=17,),(,22x-3y=16,,8x+11y = 37,,5x+3y=14,):}and also solve the system of equations in each case. |
|
Answer» Solution :(i) GIVEN equations are7x - 2y = 3 ….(1) 22x - 3y = 16 ….(2) Here, `a_(1) = 7, b_(1) = - 2`and `c_(1) = 3` [from (1)] `a_(22) = 22, b_(2) = - 3` and `c_(2) = 16`[from (2)] Now,`(a_(1))/(a_(2)) = (7)/(22)` and `(b_(1))/(b_(2)) = (-2)/(-3)=(2)/(3)` Since `(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`. HENCE, the given system has a unique solution. By cross multiplication method, we have 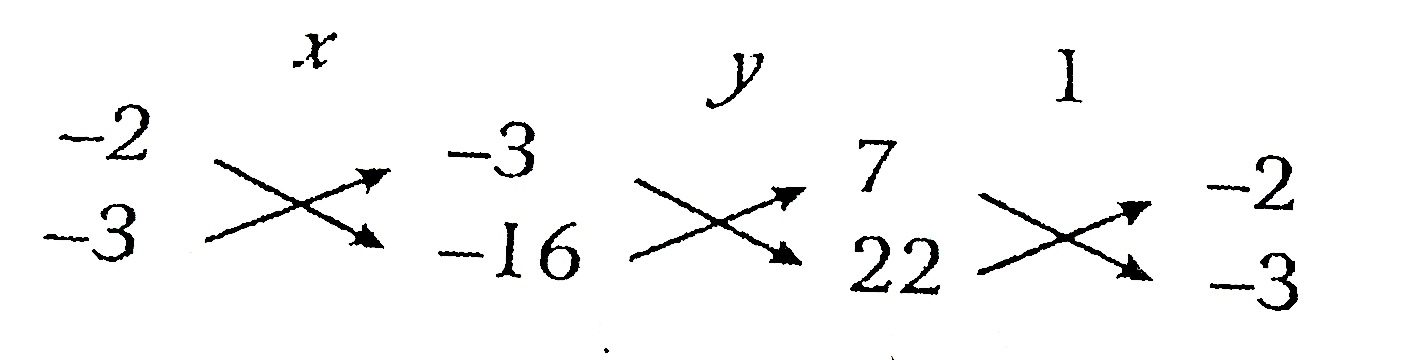 `(x)/((-2)xx(-16)-(-3)xx(-3))=(y)/((-3)xx22-(-16) xx7)=(1)/(7xx (-3) - 22 xx (-2))` `implies (x)/(32-9) = (y)/(-66 + 112) = (1)/(-21+44)` implies`(x)/(23) = (y)/(46) = (1)/(23)` When`(x)/(23) = (1)/(23) implies x = 1` and`(y)/(46) = (1)/(23) implies y = 2` Hence, `{:(x=1),(y=2):}}` is the required solution. (ii) The given system of equations is 3x + y = 17 ....(1) 8x + 11y = 37 ....(2) Here `a_(1) = 3, b_(1) = 1`and `c_(1) = 17`[from (1)] `a_(2) = 8, b_(2) = 11` and `c_(2) = 37` [from(2)] Now`(a_(1))/(a_(2)) = (3)/(8), (b_(1))/(b_(2)) = (1)/(11)` Since`(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`.Hence, the given system has a unique solution. We can write the equations as `3x + y - 17 = 0 and 8x + 11y - 37 = 0` By cross multiplication method, we have 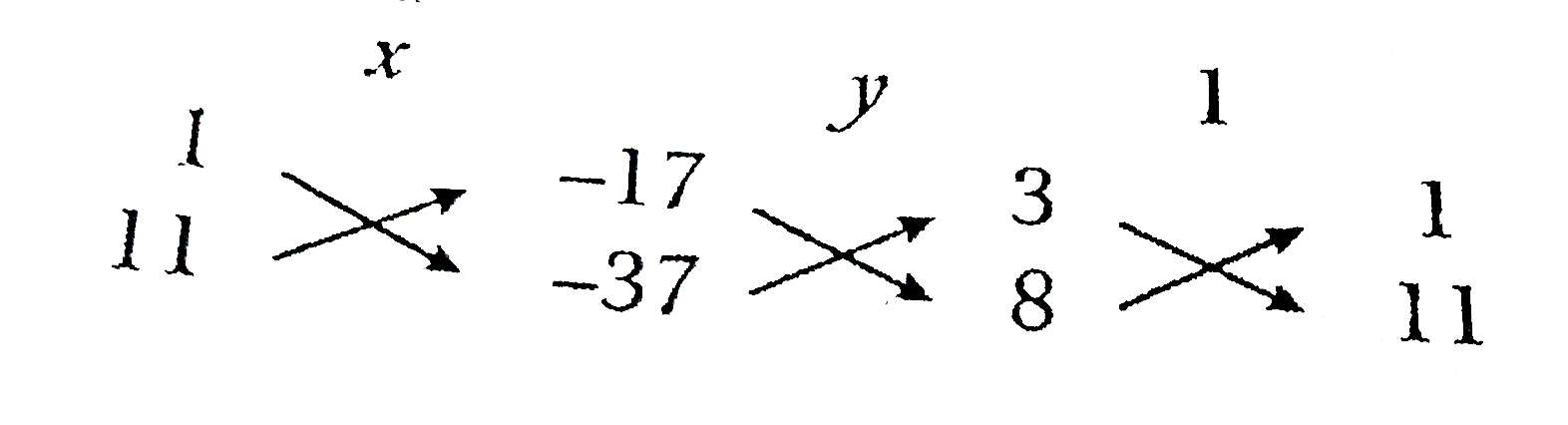 `(x)/(1xx(-37)-11xx(-17))=(y)/((-17)xx8-(-37)xx3)=(1)/(3xx11-8xx1)` implies`(x)/(150) = (y)/(-25) = (1)/(25)`When `(x)/(150) = (1)/(25) implies x = 6` and`(y)/(-25) = (1)/(25) implies y = - 1` Hence,`{:(x = 6),(y = -1):}}`is the required solution. (iii) The given system of equations is 2x + 5y - 17 = 0....(1) 5x + 3y - 14 = 0....(2) Here,`a_(1) = 2,b_(1) = 5` and `c_(1) = - 17`[from (1)] `a_(2) = 5, b_(2) = 3` and `c_(2) =- 14`[from (2)] Now,`(a_(1))/(a_(2))=(2)/(5), (b_(1))/(b_(2)) = (5)/(3)` Since`(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`.Hence, the given systemof equations has a unique solution. By cross multiplication method, we have  `(x)/(5xx (-14)-3xx(-17))=(y)/((-17)xx5-(-14)xx2)=(1)/(2xx3-5xx5)` implies`(x)/(-70 + 51) = (y)/(-85 + 28) = (1)/(6-25)` implies`(x)/(-19) = (y)/(-57) = (1)/(-19)` impliesWhen`(x)/(-19) = (1)/(-19) implies x = 1` and`(y)/(-57) = (1)/(-19) implies y = 3` Hence,`{:(x = 1),(y = 3):}}` is the required solution. |
|
| 1965. |
State with reason, whether the following are true of false. A, B and C are matrices of order 2 xx 2. (B.C).A=B.(C.A) |
|
Answer» |
|
| 1966. |
Show that (Sin theta)/(1+cos theta)+ (1+ Cos theta)/(Sin theta ) = 2 cosec theta |
|
Answer» |
|
| 1967. |
A superfast train runs having the speed15 kms / hr more than that of an express train. Leaving same station the superfast train reached at a station of 180 kms distance 1 hour before than the express train. Determine the speed of the superfast train in km/ hr. |
|
Answer» Solution :Let the speed of the superfast train was x KM/hr. `:.` the speed of the express train was (x-5)km/hr. `:.` to travel 180 km, time taken by the superfast train is `(180)/(x)` hr and by express train is `(180)/(x-15)` hr As per questions, `(180)/(x-15)-(180)/(x)=1` or, `180((1)/(x-15)-(1)/(x))=1or,(x-x+15)/((x-15)x)=(1)/(180)` or, `(15)/(x^(2)-15x)=(1)/(180)` or, `x^(2)-15x=2700` or, `x^(2)-15x-2700=0...............(1)` Comparing (1) with `ax^(2)+bx+c=0,(ANE0)` we get, `a=1,b=-15 andc=-2700` `:.` by Sreedhar Acharya's formula we get, `x=(-(-15)pmsqrt((15)^(2)-4xx1xx(-2700)))/(2xx1)` or, `x=(15pmsqrt(225+10800))/(2)` or, `x=(15pmsqrt(11025))/(2)or,x=(15pm105)/(2)` `:.x=(15+105)/(2)` (taking +sign) and `:.x=(15-105)/(2)` (taking -sign) `=(120)/(2)andx=(-90)/(2)` =60 and x=-45 But the speed of a train connot be negative, `:.x=60`. Hence the speed of the superfast train was 60 km/hr. |
|
| 1968. |
If alpha and beta be the two zeroes ofthe quadratic polynomial p(x) = 2x^(2) - 3x + 7 , evaluate . i] alpha^(3)+ beta^(3) ii] (1)/(2 alpha - 3) + (1)/( 2 beta - 3) |
|
Answer» ii] `(-3)/(14)` |
|
| 1969. |
Raju starts from a point 'P' to the North and goes 30 metre and then turns left side and goes 40 metre and reaches point Q. What is the minimum distance from P to Q and in which direction Q is from P? |
|
Answer» 50 m NORTH East |
|
| 1970. |
A man saves Rs 16,500 in ten years. In each year after the first he saved Rs. 100 more than he did in the preceding year. How much did he save in the first year? |
|
Answer» |
|
| 1971. |
BL and CM are medians of a triangle ABC right angled at A. Prove that4(BL^(2) + CM)^(2) = 5 BC^(2) . |
|
Answer» |
|
| 1972. |
A solid consisting of a right circular conce of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of wate such that it touches the bottom. Find the volume of water left in the cylinder. if the radius of the cylinder is 60 cm and its height is 150 cm. |
|
Answer» |
|
| 1973. |
Using a graph paper, plot the points A (6, 4)and B(0, 4). Find its perimeter. |
|
Answer» |
|
| 1974. |
If A={0,2,4,6}, B={3,5, 7} and C={p, q, r}, then fill the appropriate symbol in or cancel(in) or in the blanks (i) 0.....A (ii) 3....C (iii) 4....B (iv) 8....A (v) p....C (vi) 7.....B |
|
Answer» |
|
| 1975. |
If x^3+ ax^2+ bx + 6 has x -2 as a factor and leaves a remainder 3 when divided by x- 3, find the values of a and b. |
|
Answer» |
|
| 1976. |
What is the number of straight lines in the following figure |
|
Answer» 10 |
|
| 1977. |
Given matrix B=[{:(,1,1),(,8,3):}]. Find the matrix X if, X=B^2-4B. Hence, solve for a and b given X[{:(,a),(,b):}]=[{:(,5),(,50):}]. |
|
Answer» |
|
| 1978. |
Find the standard deviation of the marks obtained by you in all five subjects in the quarterly examination and in the midterm test separately. What do you observe from you results? |
|
Answer» |
|
| 1979. |
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC are of lengths 6 cm and 9 cm respectively. If the area of triangleABC = 54 cm^(2), then find the lengths of sides AB and AC. ltBRgt |
|
Answer» |
|
| 1980. |
Find the sum of first: a] 13 term of AP 2, 6, 10, 14, ..... b] 20 terms of AP -6, 0, 6, 12, ...... c] 15 term of AP 18, 16, 14, ......... |
|
Answer» b] `= 10 [ -12 + 114] = 10 xx 102 = 1020`. c] `= (15)/(2)[ 16 - 28] = (15)/(2)xx - 12 = -90`. |
|
| 1981. |
Is 402 a term of the sequence : 8, 13, 18, 23, ................. ? |
|
Answer» |
|
| 1982. |
Find the sums sums given below : 7 + 10(1)/(2)+14+....+84 |
|
Answer» |
|
| 1983. |
The table below gives the percentage distribution of female teachers in the primary schools of rural areas of various states and union territories (U.T) of India. Find the mean percentage of female teachers using all the three methods. |
|
Answer» |
|
| 1984. |
Draw an equilateral triangle of sides 5 cm and then draw circumcircle of that triangle . Also draw three tangents at A, B and C respectively. |
Answer» SOLUTION :
|
|
| 1985. |
Which of the alternatives will come next in the series. ZUA, XOC, VE, TEG, ? |
|
Answer» RAI |
|
| 1986. |
State whether the following are true or false (b) latus rectum is the smallest focal chord of any parabola |
|
Answer» |
|
| 1987. |
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid. |
|
Answer» |
|
| 1988. |
Divide 2x^(2)+3x+1 by x+2. |
|
Answer» |
|
| 1989. |
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60^(@) to 30^(@), respectively. Find the height of the poles and the distances of the point from the poles. |
|
Answer» |
|
| 1990. |
The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C''. Write down a single transformation that maps triangle ABC onto triangle A"B"C". |
|
Answer» |
|
| 1991. |
Water is flowing at the rate of 15km/hour through a pipe of diameter 14cm into a cuboidal pond which is 50m long and 44m wide. In what time will the level of water in the pond rise by 21cm? |
|
Answer» Solution :QUANTITY of WATER FLOWING through pipe in 1 hour `= pi xx (7)/(100)xx (7)/(100) xx 15000m^(3)` Required time `= (50 xx 44 xx (21)/(100))div (pi xx (7)/(100) xx (7)/(100) xx 15000)` = 2 hours |
|
| 1992. |
The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C''. Write down the co-ordinates of A", B" and C". |
|
Answer» |
|
| 1993. |
Construct a tangent to a circle of radius 4.1cm at any point . |
| Answer» | |
| 1994. |
Find the values of k for each of the quadratic equations, so that they have two equal roots. 2x^(2)+kx+3=0 |
|
Answer» |
|
| 1995. |
Solve the pair of linear equations graphically : 2x-y=2 and 2x-3y=-6 using graphicalmethod. |
|
Answer» |
|
| 1996. |
Find the coordinates of the third vertex of an equilateral triangle, whose two vertices are (3, 4) and (-2, 3). |
|
Answer» |
|
| 1997. |
A container shaped a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, making a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream. |
|
Answer» |
|
| 1998. |
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6). |
|
Answer» |
|
| 1999. |
If DeltaABC~DeltaPQR, AB = 7 cm, PQ = 12.5 cm, and the perimeter of DeltaABC=70cm, find the perimeter of DeltaPQR. |
|
Answer» |
|