3694 + Interview Questions in Maths in Class 10 Page 42 InterviewSolution

2051.	Find the roots of the following quadratic equations, if they exist. 4x^(2)+4sqrt(3)x+3=0
Answer» ANSWER :`(-SQRT(3))/(2), (-sqrt(3))/(2)`

Discussion

2052.	Prove that((1-sinalpha)/(cosalpha)+(cosalpha)/(1+sinalpha))((secalpha+(1)/(cotalpha))=2
Answer»

Discussion

2053.	If b^(2) - 4ac ge 0 then write the roots of a quadratic equation ax^(2) + bx + c = 0
Answer» Answer :`(- b + SQRT (b^(2) - 4ac))/(2A) and (-b-sqrt(b^(2) - 4ac))/(2a)`

Discussion

2054.	Represent the following situations in the form of quadratic equations : The area of a rectangular plot is 528 m^(2)The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Answer» ANSWER :`2X^(2)+x-528=0`(x=Breadth)

Discussion

2055.	A bag contains 6 white balls numbered 1 to 6 and 4 red balls numbered 7 to 10. Find the probability of getting a: (a) red ball with even number on it. (b) an odd number ball.
Answer» ANSWER :`(a)(1)/(5) (B) (1)/(2)`

Discussion

2056.	A spherical balloon of radius r subtends an angle theta at the eye of an observer. If the angle of elevation of its centre is phi, find the height of the centre of the balloon.
Answer» Answer :`R SIN phi "COSEC"(THETA)/(2)`

Discussion

2057.	find the values of k for each of the following quadratic equations, so they have equal roots: 2x^2+kx+3=0
Answer»

Discussion

2058.	(2 + sqrt(2)) is
Answer» an integer a RATIONAL number an irrational number none of these Answer :C

Discussion

2059.	Describe the locus of points at distances less than 3 cm from a given point.
Answer» ANSWER :3 CM

Discussion

2060.	Which of the following is the solution set of \|(2)/(3)u-5\|gt 8 ?
Answer» `{u: -(39)/(2)LT u lt (9)/(2)}` `{u : -(9)/(2) lt u lt (39)/(2)}` `{u : u gt (39)/(2)` or `u lt -(9)/(2)}` `{u : u gt (9)/(2)` or `u lt -(39)/(2)}` Solution :What does it MEAN if `\|(2)/(3)u-5\|gt 8` ? It means if the expression between the ABSOLUTE value bars is positive, it's greater than `+8` or, if the expression between the bars is negative, it's less than `-8`. In other words, `(2)/(3)u-5` is outside the range of `-8` to `+8` : `{:((2)/(3)u-5 gt8" "),(""(2)/(3)u gt 13),(""u gt (39)/(2)):} {:(" "(2)/(3)u-5 lt -8),(""(2)/(3)u lt - 3),(""u lt - (9)/(2)):}` In fact, there's a general rule that applies here : To solve an inequality in the form \|Whatever\| lt p, where `p gt 0` , just put that ''Whatever'' inside the range `-p` to p: \|Whatever\| lt p means -plt whateverltp For example, `\|x-5\|lt 14` becomes `-14 lt x - 5 lt 14`.

Discussion

2061.	Which one of the following statements if False?
Answer» Every set is SUBSET of itself EMPTY set is subset of every set Intersection of TWO disjoint sets is empty set Cardinal number of an INFINITE set is zero Answer :B

Discussion

2062.	A pipe of diameter 7 cm is connected with a cylindrical tank of oil which is 10.5 metres long. Ifoil is drawn out at the rate of 210 metres per minute through the pipe, the tank full ofoil becomes empty in 45 minutes. Find the diameter of thetank.
Answer» ANSWER :60 CM (APPROX.)

Discussion

2063.	If 2 is subtracted from the numerator and 3 is added to the demoenator a fraction becomes (1)/(4). Again if 6 is added to the numerator and the denomenator is multiplied by 3, then it becomes (2)/(3). Determine the fraction.
Answer» ANSWER :`(4)/(5);`

Discussion

2064.	Find the area of the shaded region given in figure.
Answer» SOLUTION :Join JK, KL, LM and MJ. There are FOUR equally semi - circlesand LMHK formed a SQUARE. `:. FH = 14 - (3 + 3) = 8 cm` So, the side of square should be 4 cm and radius of semi - circle of both endsare 2 cm each. `:.` AREA of square JKLM = `(4)^(2) = 16 cm^(2)` Area of semi - circle HJM = `(pir^(2))/(2)` = `(pixx(2)^(2))/(2)=2pi cm^(2)` `:.` Area of four semi - circle = `4xx6.28 = 25 12 cm^(2)` Now, area of square ABCD = `(14)^(2) = 196 cm^(2)` `:.` Area of shaded region = Area of square ABCD - [Area of four semi - circle + Area of square JKLM] = `196 - [8pi + 16] = 196 - 16 - 8pi` = `(180 - 8 pi) cm^(2)` Hence , the required of the shaded region is `(180 - 8 pi)cm^(2)` .

Discussion

2065.	Find all the zeroes of 2x^(4)-3x^(3)-3x^(2)+6x-2, if you know that two of its zeroes are sqrt(2) and -sqrt(2).
Answer» ANSWER :`SQRT(2),-sqrt(2),1" and " 1/2`.

Discussion

2066.	Evaluate cosec 31^(@) -sec 59^(@)
Answer» ANSWER :`0`

Discussion

2067.	Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer» SOLUTION :Given, two concentric circles of radill 4 cm and 6 cm with common centre O. We have to draw two tangents to inner circle from a point of outer circle. Steps of Construction : 1. Draw two concentric circles with centre a O and radii 4 cm and 6 cm. 2. Take any point P on outer circle. Join OP. 3. Now, bisect OP. LET M' be the mid-point of OP. 3. Now, bisect OP. Let M' be the mid-point of OP. Taking M' as centre and OM' as radius draw a circle (dotted) which cuts the inner circle at M and P'. 4. Join PM and PP'. Thus, PM and PP' are required tangents. 5. On measuting PM and PP', we get PM = PP' = 4.47 cm. Calculation : In right `DeltaOMP,anglePMO=90^(@)` `therefore""PM^(2)=OP^(2)-OM^(2)""("by Pythagoras theorem")` `implies""PM^(2)=(6)^(2)-(4)^(2)=36-16=20` `implies""PM=sqrt20=44.47` Hence, the lenght of tangent is `4.47.` Justification : Join OM and OP' which are radius. The `angle OMP` is an angle lies in the semi-circle and therefore `angleOMP=90^(@)` `implies""OMbotOP` Since, Om is radius of the circle, so MP has to be a tangent to the circle. Similarly, PP' is also a tangent to the circle.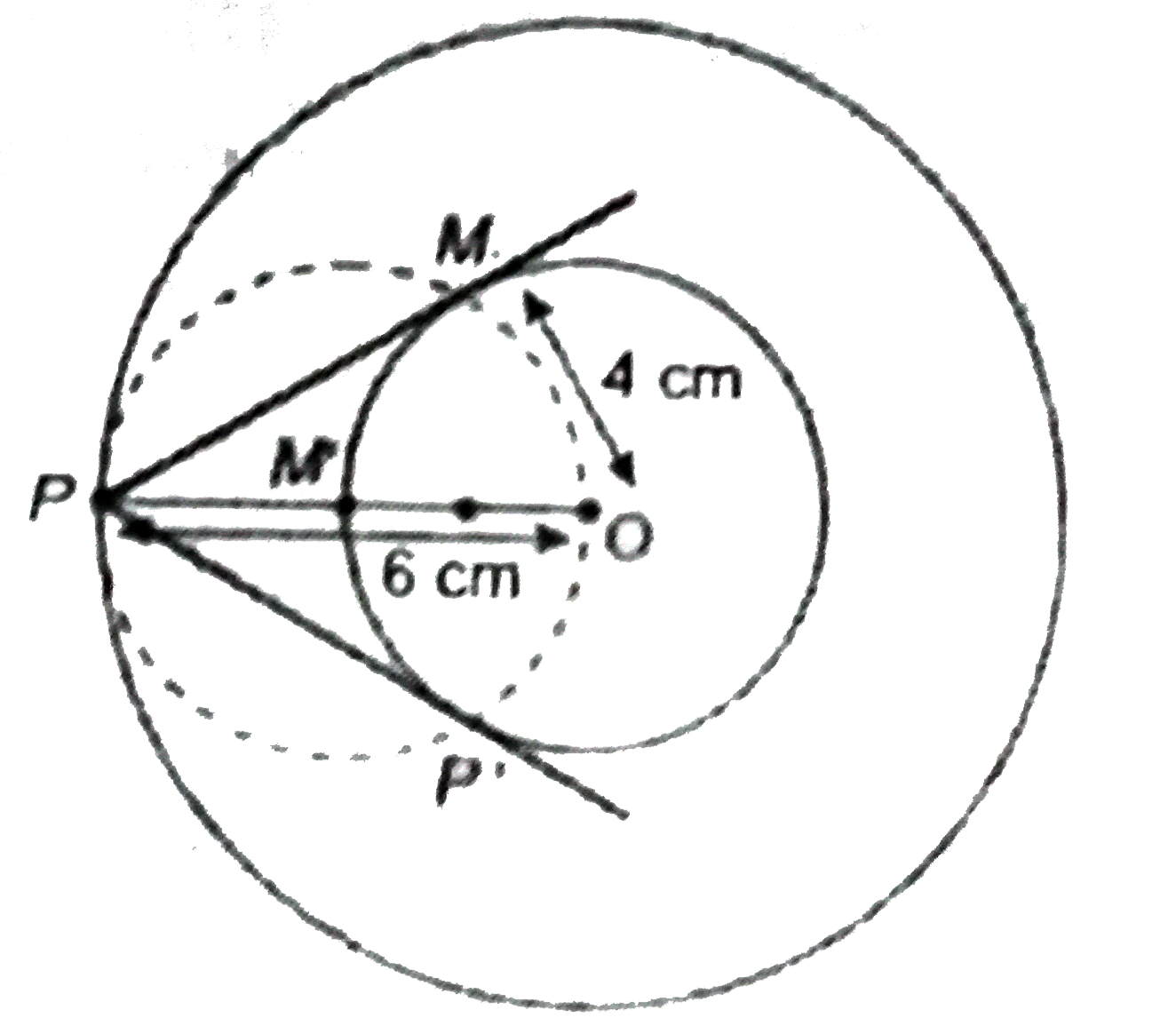

Discussion

2068.	Mr. Solanki sold 2 water filter and taxable value of each filter is 6500. If the rate of GST is 18% then find the amount of GST charged in the tax invoice.
Answer» ANSWER :2340

Discussion

2069.	The product of two numbers is 12. If their sum added to the sumof their squares is 32, find the numbers.
Answer» ANSWER :`-6,-2or4,3`

Discussion

2070.	Find the coefficient of x^(3),x^(2),xandx^(0) of the equation (x-1)^(5)=x(x^(4)+1)
Answer» ANSWER :COEFFICIENT of `x^(2)=-10,` coefficient of `x^(2)=10` coefficient of x=-4 and coefficient of `x^(0)=1;`

Discussion

2071.	Find the value of k for which the system of equations x + 3y -4 =0 and 2x + ky =7 is inconsistent.
Answer» ANSWER :6

Discussion

2072.	Vinay and Praveen working together can paint the exterior of a house in 6 days. Vinay by himself can complete the job in 5 days less than praveen. How long will it take Vinay to complete the job by himself?
Answer» Answer :TIME TAKEN by PRAVEEN = x + 5 = 15 days.

Discussion

2073.	If the 4^(th),7^(th) and 10^(th) terms of a G.P. are a, b and c respectively, prove that : b^(2)=ac
Answer» ANSWER :`:.""B^(2)=AC`

Discussion

2074.	Find the sum of the G.P. : 2+6+18+54+ . . . . . . . .. +4374.
Answer» ANSWER :6560

Discussion

2075.	Find the 11th term from the last of the AP series given below: AP: 10,7,4,….,-62
Answer» ANSWER :`-32`

Discussion

2076.	In the given figure , CM and RN are respectivelythe median of triangles ABC and PQR IFDelta ABCis similar to Delta PQR,prove that (i)Delta AMC ~ Delta PNR (ii)(CM)/(RN)= (AB)/(PQ)and(iii)Delta CMB ~ Delta RNQ
Answer» ANSWER :` 4 : 49 `

Discussion

2077.	If 7^(logx)+x^(log7) = 98,then log_(10)sqrt(x) = ______.
Answer» 47 51 14 49 Solution :(i) Use log a + log B = log ab and remove logarithms on both the sides and evaluate `(a-b)^(2)`. (ii) Express RHS into single logarithm with COEFICIENT 1. (iii) Apply antilog and cancel the logarithms on both sides. (iv) Divide LHS and RHS by ab and OBTAIN the REQUIRED value.

Discussion

2078.	The radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
Answer» Solution :Produce BD to E which CUTS the circle at E. Join AE and OD. Since AB is the diameter of bigger circle. `:.""angleAEB=90^(@)""`(angle in a semicircle is right angle) ALSO, `angleODB=90^(@)""`(radius through point of contact is `_\|_` to the tangent) Now, in `triangleBOD` and `triangleBAE` `angleB=ANGLEB""`(common) `angleODB=angleAEB""`(EACH `90^(@)`) `:.""triangleBOD~triangleBAE""`(AA corollary) `:.""(OD)/(AE)=(OB)/(AB)""`(corresponding sind of similar triangles are proportional) `implies""(8)/(AE)=(r)/(2r)""implies""AE=16cm` Since, `OD_\|_EB` `:.""DE=DB""`(`_\|_` drawn from the centre to the CHORD BISECTS the chord) In right `triangleODB,` `DB^(2)=OB^(2)-OD^(2)` `= (13)^(2)-(8)^(2)=169-64=105` `:.""DB=sqrt(105)cm=ED` Now, in right `triangleAED,` by Pythagoras theorem `AD^(2)=AE^(2)+ED^(2) ` `implies""AD^(2)=(16)^(2)+105=256+105=361` `implies""AD=sqrt(361)` i.e., `19 cm` Hence, `""AD=19cm.`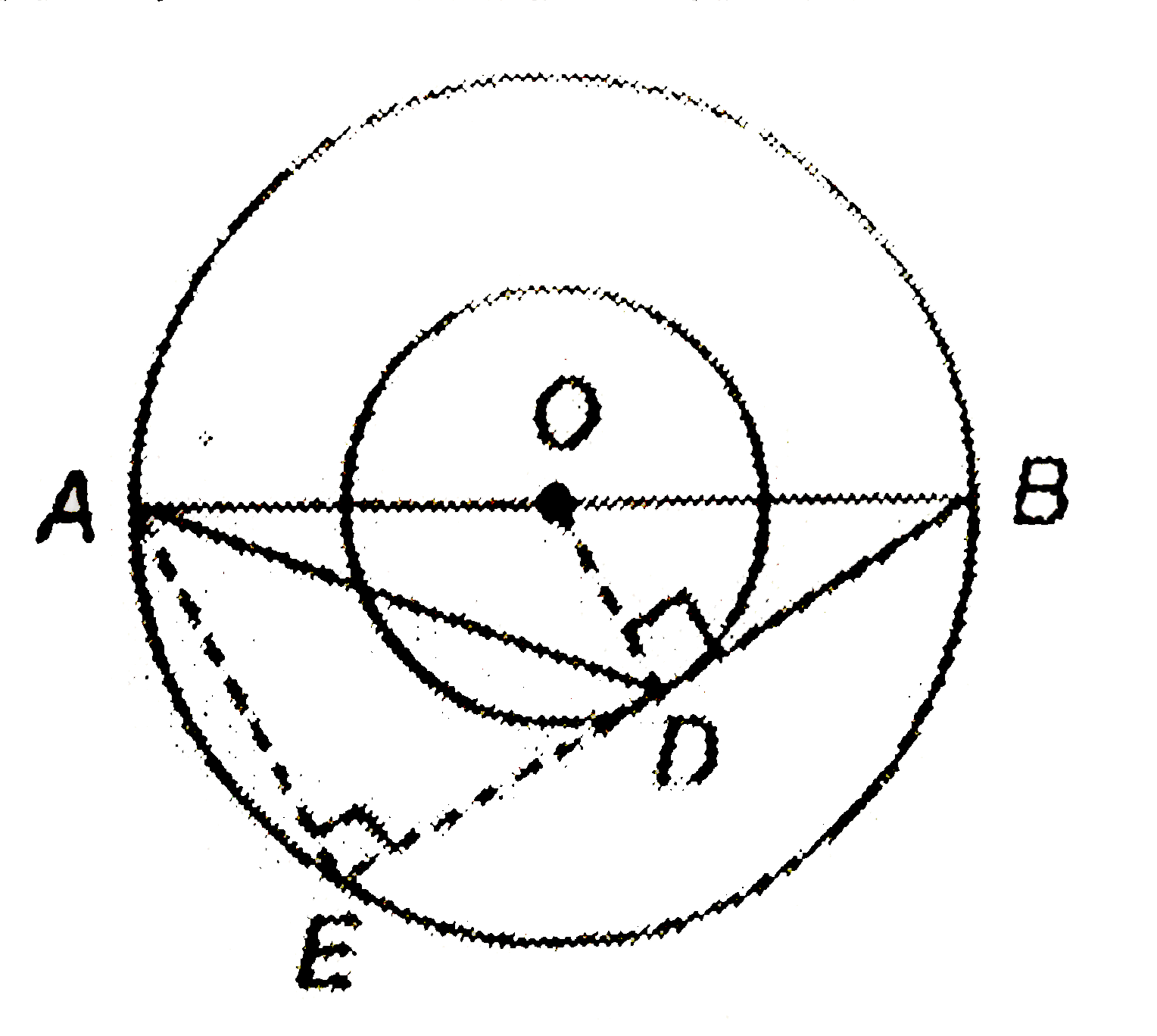

Discussion

2079.	Find two such numbers whose sum is 27 and product is 182.
Answer» ANSWER :`11,13`

Discussion

2080.	Solve the following quatratic equation : 4x^(2)-2(a^(2)+b^(2))x+a^(2)b^(2)=0
Answer» Solution :Given equation is `4x^(2)-2(a^(2)+b^(2))x+a^(2)b^(2)=0` `implies4x^(2)-2A^(2)x-2b^(2)x+a^(2)b^(2)=0` `implies2x(2x-a^(2))-b^(2)(2x-a^(2))=0` `IMPLIES(2x-a^(2))(2x-b^(2))=0` `implies2x-a^(2)=0or2x-b^(2)=0` when `2x-a^(2)=0impliesx=(a^(2))/(2)` and `2x-b^(2)=0impliesx=(b^(2))/(2)` HENCE, `a^(2)/(2)and(b^(2))/(2)` are ROOTS of the equation.

Discussion

2081.	A dice is thrown two times. Find the probability that the product of numbers of the dice is : 6
Answer» ANSWER :`1/9`

Discussion

2082.	The sum of the first three terms of an Arithmeic Progression (A.P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference.
Answer» Answer :if FIRST TERM = 26, common difference = -12 and, if first term = 2, common difference = 12

Discussion

2083.	Some goods/services are supplied for Rs 20,000 from Mathura (U.P.) to Ratlam (M.P.) and then from Ratlam to Indore (M.P.). If at each stage, the rate of tax under GST system is 12% and the profit made by the dealer in Ratlam is Rs 3,750, find the cost of the article (in Indore) under GST.
Answer» ANSWER :RS 26,600

Discussion

2084.	If x=(1sintheta)/(costheta), prove that :sintheta=(x^(2)-1)/(x^(2)+1)
Answer»

Discussion

2085.	In the given figure , angle1=angle2 and angle3 = angle4. If BC= 7.5 cm , DE= 12.5cm and area oftriangle ABC= 13.5 cm^(2) . Find the area of triangleADE.
Answer» ANSWER :`37.5cm^(2)`

Discussion

2086.	Rekha has 15 square 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …, 24 cm. How much are can be decorated with these colour papers?
Answer» ANSWER :4615`CM^(2)`

Discussion

2087.	Construct a right-triangle where the sides (other than the hypotenuse) are of lengths 5 cm and 7 cm. Then, construct another triangle whose sides are (4)/(5) times the corresponding sides of the given triangle.
Answer» ANSWER :`(AB')/(AB )= (B' C')/(BC )= (AC ')/(AC ) = (4)/(5)`.

Discussion

2088.	Determine the value of the following. log_(2/3)(8/27)
Answer» ANSWER :3

Discussion

2089.	In the given figure ,I is the incentre of triangle ABC . AIproduced meets the circumcircle of the triangle ABC at point D. ifangle BAC = 50^(@) and angle ABC = 70 ^(@),find : (i)angle BCD (ii) angle ICD (iii)angle BIC (##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">
Answer» ANSWER :` 25 ^(@) (II)25^(@) (III) 115 ^(@) `

Discussion

2090.	A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank is 60^(@). When he retreates 20m from the bank, he observes the angle of elevation of the top of the same tree to be 30^(@). Find the height of the tree and the breadth of the river.
Answer» ANSWER :`10 sqrt3m`, 10M`

Discussion

2091.	A vessel is in the form of an inverted cone. Its height is 8 cm. and the radius of its top is 5 cm.It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, 1/4 of the water flows out. Find the number of lead shots dropped into the vessel.
Answer» ANSWER :100

Discussion

2092.	Mr. Gupta has a choice to invest in ten-rupee shares of two firms at 13rs or at 16rs. If the first firm pays 5% dividend and the second firm pays 6% dividend per annum, find : (i) which firm is paying better (ii) if Mr. Gupta invests equally in both the firms and the difference between the returns from them is 30rs, find how much, in all does he invest ?
Answer» ANSWER :`(i)` FIRST FIRM `(II) 62400rs`

Discussion

2093.	If x, y, z are real numbers satisfying the equation 25(9x^(2)+y^(2))+9z^(2)-15(5xy+yz+3zx)=0 , then prove that x, y and z are in A.P.
Answer» Solution :We hare, `25(9x^(2)+y^(2))+9z^(2)-15(5xy+yz+3zx)=0` `rArr (15X)^(2)+(5y)^(2)+(3z)^(2)-(15x)(5y)-(5y)(3z)-(3z)(15x)=0` `rArr (1)/(2)[2(15x)^(2)+2(5y)^(2)+2(3z)^(2)-2(15x)(5y)-2(5y)(3z)-2(3z)(15x)]=0` `rArr (1)/(2)[(15x-5y)^(2)+(5y-3z)^(2)+(3z-15x)^(2)]=0` `rArr (15x-5y)^(2)+(5y-3z)^(2)+(3z-15x)^(2)=0` It is possible only when `15x-5y=0 and 5y-3z=0 and 3z-15x=0` `rArr 15x=5y=3z` `rArr (x)/(1)=(y)/(3)=(Z)/(5)=K` (say) `:. x=k, y=3k, z=5k` Now, `y-x=3k-k=2k` and`z-y=5k-3k=2k` Since, `y-x=z-y` `:. x,y,z ` are in A.P. `""` Hence Proved

Discussion

2094.	IF the area of a sector is 7/20 of the area of the circle, the sector angle is
Answer» `90^@` `100^@` `126^@` `110^@` ANSWER :C

Discussion

2095.	Evaluate : [{:(,4 sin 30^@2 cos 60^@), (,sin 90^@2 cos 0^@):}] [{:(,4,5),(,5,4):}]
Answer» ANSWER :`[{:(,13,14),(,14,13):}]`

Discussion

2096.	Gopal has some 100rs shares of company A, paying 10% dividend. He sells a certain number of these shares at a discount of 20% and invests the proceeds in 100rs shares of 60rs of company B paying 20% dividend. If his income from the shares sold increases by 18000rs find the number of shares sold by Gopal
Answer» ANSWER :1080

Discussion

2097.	The point P (2,-4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
Answer» ANSWER :Q = (-2,-4)

Discussion

2098.	sin 60 ^@ cos30 ^@+sin30^ @cos60^@ = ?
Answer» ANSWER :`1`

Discussion

2099.	Prove that : (sin A + "cosec" A)^2 + (cos A + sec A)^2 = 7 + tan^2 A + cot^2 A.
Answer» ANSWER :`40 SQRT(3)m`

Discussion

2100.	Neha went to a 'sale' to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered, 'the number of skirts are two less then twice the number of pants purchesed and the number of skirts is four less than four times the number of pants purchased." Help her friend to find how many pants and skirts Neha bought.
Answer» ANSWER :NUMBER of parts = 1;Number of SHIRTS = 0

Discussion

Explore topic-wise InterviewSolutions in .

Find the roots of the following quadratic equations, if they exist. 4x^(2)+4sqrt(3)x+3=0

Prove that((1-sinalpha)/(cosalpha)+(cosalpha)/(1+sinalpha))((secalpha+(1)/(cotalpha))=2

If b^(2) - 4ac ge 0 then write the roots of a quadratic equation ax^(2) + bx + c = 0

Represent the following situations in the form of quadratic equations : The area of a rectangular plot is 528 m^(2)The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.

A bag contains 6 white balls numbered 1 to 6 and 4 red balls numbered 7 to 10. Find the probability of getting a: (a) red ball with even number on it. (b) an odd number ball.

A spherical balloon of radius r subtends an angle theta at the eye of an observer. If the angle of elevation of its centre is phi, find the height of the centre of the balloon.

find the values of k for each of the following quadratic equations, so they have equal roots: 2x^2+kx+3=0

(2 + sqrt(2)) is

Describe the locus of points at distances less than 3 cm from a given point.

Which of the following is the solution set of |(2)/(3)u-5|gt 8 ?

Which one of the following statements if False?

A pipe of diameter 7 cm is connected with a cylindrical tank of oil which is 10.5 metres long. Ifoil is drawn out at the rate of 210 metres per minute through the pipe, the tank full ofoil becomes empty in 45 minutes. Find the diameter of thetank.

If 2 is subtracted from the numerator and 3 is added to the demoenator a fraction becomes (1)/(4). Again if 6 is added to the numerator and the denomenator is multiplied by 3, then it becomes (2)/(3). Determine the fraction.

Find the area of the shaded region given in figure.

Find all the zeroes of 2x^(4)-3x^(3)-3x^(2)+6x-2, if you know that two of its zeroes are sqrt(2) and -sqrt(2).

Evaluate cosec 31^(@) -sec 59^(@)

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Mr. Solanki sold 2 water filter and taxable value of each filter is 6500. If the rate of GST is 18% then find the amount of GST charged in the tax invoice.

The product of two numbers is 12. If their sum added to the sumof their squares is 32, find the numbers.

Find the coefficient of x^(3),x^(2),xandx^(0) of the equation (x-1)^(5)=x(x^(4)+1)

Find the value of k for which the system of equations x + 3y -4 =0 and 2x + ky =7 is inconsistent.

Vinay and Praveen working together can paint the exterior of a house in 6 days. Vinay by himself can complete the job in 5 days less than praveen. How long will it take Vinay to complete the job by himself?

If the 4^(th),7^(th) and 10^(th) terms of a G.P. are a, b and c respectively, prove that : b^(2)=ac

Find the sum of the G.P. : 2+6+18+54+ . . . . . . . .. +4374.

Find the 11th term from the last of the AP series given below: AP: 10,7,4,….,-62

In the given figure , CM and RN are respectivelythe median of triangles ABC and PQR IFDelta ABCis similar to Delta PQR,prove that (i)Delta AMC ~ Delta PNR (ii)(CM)/(RN)= (AB)/(PQ)and(iii)Delta CMB ~ Delta RNQ

If 7^(logx)+x^(log7) = 98,then log_(10)sqrt(x) = ______.

The radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.

Find two such numbers whose sum is 27 and product is 182.

Solve the following quatratic equation : 4x^(2)-2(a^(2)+b^(2))x+a^(2)b^(2)=0

A dice is thrown two times. Find the probability that the product of numbers of the dice is : 6

The sum of the first three terms of an Arithmeic Progression (A.P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference.

Some goods/services are supplied for Rs 20,000 from Mathura (U.P.) to Ratlam (M.P.) and then from Ratlam to Indore (M.P.). If at each stage, the rate of tax under GST system is 12% and the profit made by the dealer in Ratlam is Rs 3,750, find the cost of the article (in Indore) under GST.

If x=(1sintheta)/(costheta), prove that :sintheta=(x^(2)-1)/(x^(2)+1)

In the given figure , angle1=angle2 and angle3 = angle4. If BC= 7.5 cm , DE= 12.5cm and area oftriangle ABC= 13.5 cm^(2) . Find the area of triangleADE.

Rekha has 15 square 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …, 24 cm. How much are can be decorated with these colour papers?

Construct a right-triangle where the sides (other than the hypotenuse) are of lengths 5 cm and 7 cm. Then, construct another triangle whose sides are (4)/(5) times the corresponding sides of the given triangle.

Determine the value of the following. log_(2/3)(8/27)

In the given figure ,I is the incentre of triangle ABC . AIproduced meets the circumcircle of the triangle ABC at point D. ifangle BAC = 50^(@) and angle ABC = 70 ^(@),find : (i)angle BCD (ii) angle ICD (iii)angle BIC (##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">

If x, y, z are real numbers satisfying the equation 25(9x^(2)+y^(2))+9z^(2)-15(5xy+yz+3zx)=0 , then prove that x, y and z are in A.P.

IF the area of a sector is 7/20 of the area of the circle, the sector angle is

Evaluate : [{:(,4 sin 30^@2 cos 60^@), (,sin 90^@2 cos 0^@):}] [{:(,4,5),(,5,4):}]

The point P (2,-4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.

sin 60 ^@ cos30 ^@+sin30^ @cos60^@ = ?

Prove that : (sin A + "cosec" A)^2 + (cos A + sec A)^2 = 7 + tan^2 A + cot^2 A.