Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

1801.

Find the centroid of the triangle whose vertices are A(-1,0), B(5, -2) and C(8, 2).

Answer»

Solution :Centroid, the point where the medians ofa triangle intersect, divides each MEDIAN in the ratio 2:1. Let AD be the median and G(x, y) be the centroid of `DeltaABC`.
`thereforeD` is the mid-point of BC.
`therefore" "D-=((5+8)/(2),(-2+2)/(0))""` (mid-point formula)
`""-=((13)/(2),0)`

Now, G(x, y) divides the line segment JOINING A(-1,0) and `D((13)/(2),0)` internally in the ratio 2 : 1.
So, by USING section formula,
`""x=(2((13)/(2))+1(-1))/(2+1)" "rArr" "x=4`
and `""y=(2(0)+1(0))/(2+1)" "rArr" "y=0`
`therefore` Centroid of `DeltaABC-=` (4, 0)
Discussion
1802.

How many spherical balls can be made out of a solid cube of lead whose edge measures 44 cm and each ball being 4 cm in diameter.

Answer»


ANSWER :2541
Discussion
1803.

Given : M =[(5,-3),(-2, 4)] find its transpose matrix M'. If possible, find : (i) M+M""^(t) (ii) M^(t)-M

Answer»


ANSWER :`M^t=[{:(,5,-2),(,-3,4):}]`(i) `[{:(,10,-5),(,-5,8):}]` (II) `[{:(,0,1),(,-1,0):}]`
Discussion
1804.

Find the volume and whole surface of frustum of a square pyramid , thje sides of whosebase and top are 24 cm and 16 cm respectively and each of the edges of the frustum is 20cm.

Answer»

Solution :Given that a =24, b cm, Edge =e=20 cm
AB=(1)/(2)`xx`Diagonal `=(1)/(2)xxasqrt(2)=(b)(sqrt(2))`
`DC=(1)/(2)xx`Diagonal `=(1)/(sqrt(2)=(a)/(sqrt(2))`
DE=DC-EC=DC-AB=`(a)(sqrt(2))-(b)/(sqrt(2))`
To find height h,
we have for sqare FRUSTUM
`e^(2)=h^(2)+(1)/(2)(24-16)^(2)`
`400=h^(2)+(1)/(2)xx8xx=h^(2)+32`
`h^(2)=400-32=368 rarrh=19.18 cm`
volume `V=(1)/(3)h(A_(1)+sqrt(A_(1)A_(2))+A_(2)`
`A_(1)=a^(2)=24^(2)=576, A_(2)=b^(2)=16^(2)=256`
`V=(1)/(3)xx19.18(576+384+256)=777.29 cm^(2)`
Total SURFACE area =slant surface + Area of the TOP and bottom faces
`=(1)/(2)` (sum of the perimeters `xx` slant height +`a^(2)+b^(2)`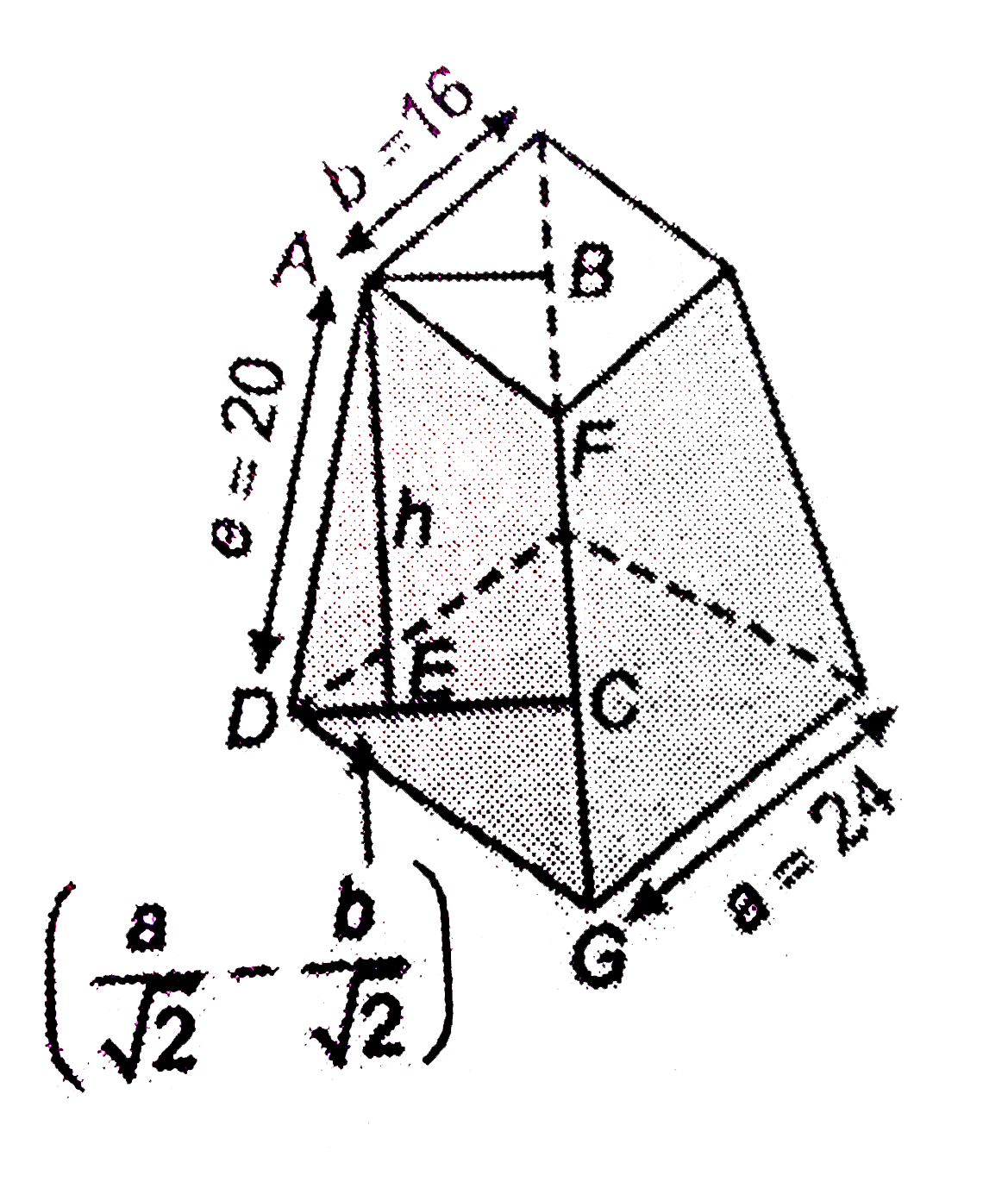

[AF=b,DG=a]
[KM=b]
But DK=MG
DK=Mg=`(a-b)/(2)`
`e^(2)=l^(2)+DK^(2)`
`e^(2)=l^(2)+((a)/(2)-(b)/(2))^(2)`
`(20)^(2)=l^(2)+((24)/(2)(16)/(2^(2)))rArr400=l^(2)+(4^(2))`
`[l^(2)`=384 `rArr l=sqrt(384)`=19.6]
Total surface area `=(1)/(20)xx4xx16xx4)xx(19.6)+24^(2)+16^(2)`
`=(1)/(2)(96+64)xx19.6+576+256`
`=(1)/(2)xx160xx19.6+576+256`
=1568+576+256=2400 `cm^(2)`
Discussion
1805.

(ii)A survey of 500 TV viewers produced the following information: 280 watch football, 150 watch hockey, 200 watch basketball, 70 watch football and basketball, 90 watch football and hockey, 80 watch hockey andbasketball and 50 watch all the three games.Then, (ii)How many viewers watch exactly two games?

Answer»


ANSWER :90
Discussion
1806.

Distance between two circles with R and r is d units. If d^2=R^2+r^2 , then the two circles __________(intersect at one point/ do not intersect /intersect at two distinct points).

Answer»


SOLUTION :N/A
Discussion
1807.

Find the mean proportional to x - y and(x-y)^(3)

Answer»


ANSWER :` ( x-y )^(2)`
Discussion
1808.

Maximum profit: An barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x) = -10x^(2) +3500x -66000where P(x) is the profitin rupeesand x is the numberof barrelsmade and sold. Based on this model answer the following questions: What is the profit/loss if 400 barrels are produced

Answer»

<P>Profit 266200
Loss 266200
Profit 342000
Loss 342000

Solution :`P(400)= - 10(400)^(2) +3500 (400) - 66000= -266000`
Thus (B) is correct OPTION.
Discussion
1809.

Maximum profit: An barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x) = -10x^(2) +3500x -66000where P(x) is the profitin rupeesand x is the numberof barrelsmade and sold. Based on this model answer the following questions: What is the maximum profit which can manufacturer earn?

Answer»

<P>Rs 240250
Rs 480500
Rs 680250
Rs 240250

Solution :Rearranging the given equation we have
`P(X) = -10X^(2) +3500x - 66000`
`= -10 (x^(2) -350x +6600)`
`= -10 [(x-175)^(2) -30625 +6600]`
`=-10 [(x-175)^(2) -24025]`
`= -10(x-175)^(2)+240250`
From above equation it is clear that maximum value of P(x) is 240250.
THUS (a) is correct option.
Discussion
1810.

Maximum profit: A barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x) = -10x^(2) +3500x -66000where P(x) is the profitin rupeesand x is the numberof barrelsmade and sold. Based on this model answer the following questions: When no barrels are produce what is a profit loss?

Answer»

22000
66000
11000
33000

Solution :When no BARRELS are produced, X = 0
`P(x) = 0+0 -6000 `
`P(x) = -66000`
Thus (B) is CORRECT option.
Discussion
1811.

Maximum profit: An barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x) = -10x^(2) +3500x -66000where P(x) is the profitin rupeesand x is the numberof barrelsmade and sold. Based on this model answer the following questions: What is the break even point ? (Zero profit point is called break even)

Answer»

10 barrels
30 barrels
20 barrels
100 barrels

Solution :At break-even point `P(x) = 0`, thus
`0 = -10x^(2) +3500x -66000`
`x^(2) +350x +6600=0`
`x^(2)-330x-20x+6600=0`
`x(x-330) -20(x+300)=0`
`(x-330) (x-20)=0`
`x=20, 330`
Thus, (c ) is correct option.
Discussion
1812.

Maximum profit: An barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x) = -10x^(2) +3500x -66000where P(x) is the profitin rupeesand x is the numberof barrelsmade and sold. Based on this model answer the following questions: What is the profit/loss if 175 barrels are produced

Answer»

Profit 266200
Loss 266200
Profit 240250
Loss 240250

Solution :`P(175) = -10 (175)^(2) +3500 (175) -66000 = 240250`
Thus (c) is CORRECT option.
Discussion
1813.

If the sum of first n terms of an A.P. is 3n^2 + 2n , find its r^(th)term.

Answer»


ANSWER :6R - 1
Discussion
1814.

A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled

Answer»


ANSWER :`4.05 CM`
Discussion
1815.

A temple and a flagstaff surmounted at its top, each subtends equal angle of30^(@) at a point on the ground. If the height of the temple is 10 m, find the height of the flagstaff.

Answer»


ANSWER :20 m
Discussion
1816.

Sum of the area of two square is 468m^(2). If the difference of their perimeters is 24m, find the sides of the two squares.

Answer»


ANSWER :`12 m and 18 m`
Discussion
1817.

Find a point on the base of a scalene triangle equidistant from its sides.

Answer»

<P>

ANSWER :P is EQUIDISTANT from AB and AC.
Discussion
1818.

In a certain language ENTRY is coded as 12345 and STEADY is coded as 931785, then state the correct code for the given word in each questions. NEATNESS

Answer»

25196577
21732199
21362199
21823698

Answer :B
Discussion
1819.

In a certain language ENTRY is coded as 12345 and STEADY is coded as 931785, then state the correct code for the given word in each questions. ARREST

Answer»

744589
744193
166479
745194

Answer :B
Discussion
1820.

Find the amount of bill for the following intra - state transaction of goods. The rate of GST is 12% Note , If for the value of any transaction, discount =30% rArr its discounted value =70% of its original value. Similarly, if for the value of any transaction, discount offered =40%, rArr its discounted value =60% of its original value.

Answer»


ANSWER :713.44
Discussion
1821.

A point P is reflected in the x - axis . Co - ordinates of its image are (8,-6). Find the co - ordinates of P.

Answer»

<P>

ANSWER :P = (8,6)
Discussion
1822.

To draw two tangents to a circle which are perpendicular to each other, the perpendiculars are to be drawn at the ends of two radii which are inclined at an angle of……..

Answer»

`120^(@)`
`60^(@)`
`30^(@)`
`90^(@)`

Discussion
1823.

if OXPY is a square of side 4 cm in first quadrant, where O is the origin. ( OY and OX are lies y-axis and x-axis respectively ). find the equation of the circle C_1,C_2,C_3,C_4 and C_5

Answer»


ANSWER :`C_1:(x-1)^(2)+(y-1)^(2)=1`
`C_2:(x-3)^(2)+(y-1)^(2)=1`
`C_3:(x-3)^(2)+(y-3)^(2)=1`
`C_4:(x-1)^(2)+(y-3)^(2)+1`
`C_5:(x-2)^(2)+(y-3)^(2)=1`
Discussion
1824.

State the reasons for the following : (i){1,2,3.....10} ne {x : x ne N and 1 lt x lt 10} (ii) {2,4,6,8,10} ne {x: x =2n+1 and x ne N} (iii) {5,15,30,45} ne {x : x is a multiple of 15} (iv) {2,3,5,7,9} ne {x : x is a prime number}

Answer»


ANSWER :(i) `{1,2,3...10} ne {2,3,4,....9}`
(ii) x=2x+1 MEANS x is odd
(iii) x is multiple of 15. So 5 does not exist
(ix) x is prime number but 9 is not a prime number
Discussion
1825.

Find the sum of first 20 terms of an AP whose nth term is a_(n) = 2-3n.

Answer»


ANSWER :`= 10 [-2-57 ] = -590`
Discussion
1826.

The perimeters of the two circualr ends of a frustum of a cone are 48 cm and 36 cm. If the height of the frustum is 11 cm, find its volume and curved surface area.

Answer»


SOLUTION :`2pir=36" and "2piR=48. "FIND R and R".`
Discussion
1827.

A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Answer»


ANSWER :7 YEARS
Discussion
1828.

Let A=[{:(,4,-2),(,6,-3):}], B=[{:(,0,2),(,1,-1):}] and C=[{:(,-2,3),(,1,-1):}]. Find A^2-A+BC.

Answer»


ANSWER :`[{:(,2,-2),(,-3,4):}]`
Discussion
1829.

Mr. Ahujahas two square plots of landwhichhe utilisesfor twodifferentpurposes -onefor providingfree education to the children below the age of 14years and the other to provide free medical servicesforthe needyvillagers. The sum of the areas of two square plots is 15425 m^(2) .If thewhichqualitiesof Mr. Ahuja are beingdepicted in the question ?

Answer»


Answer :Hence , SIDES of TWO squares are 80 m ADD 95 m.
Discussion
1830.

Find the roots of the following quadratic equations, if they exist. x^(2)+4x+5=0

Answer»


ANSWER :no REAL ROOTS
Discussion
1831.

Find the sum of the first 16 terms of a sequence whose nth term is given by t_(n)=5n-3, where n is a nautral number.

Answer»


ANSWER :632
Discussion
1832.

A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is (5159)/(6) cm ^(3), and (4235)/(6) cm ^(3) of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.

Answer»


ANSWER :`3.5 CM and 20 cm`
Discussion
1833.

Check whether the following equations are consistent or inconsistent. Solve them graphically. 2x-3y=8 , 4x-6y=9.

Answer»


ANSWER :The LINES are PARALLEL and no SOLUTION EXISTS.
Discussion
1834.

Evaluate the following 2 tan ^(2) 45^(@) +cos^(2) 30 ^(@) -sin ^(2) 60^(@)

Answer»


ANSWER :` 2`
Discussion
1835.

Spherical marbles of diameter 1-4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm ?

Answer»


ANSWER :150
Discussion
1836.

Which of the following sequqnces are in arithmetic progression? (i) 2,6,10,14,…. (ii) 15,12,9,6 (iii) 5,9,12,18,….. (iv) 1/2, 1/3, 1/4, 1/5,….

Answer»


ANSWER :(i) YES, (II) Yes (III) No (IV) No
Discussion
1837.

The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their : radii,

Answer»


ANSWER :`3:1`
Discussion
1838.

Check whether the following are quadratic equations : (x-3) (2x+1) =x(x+5)

Answer»


ANSWER :YES
Discussion
1839.

Check whether the following equations are consistent or inconsistent. Solve them graphically. (a) 3x + 2y = 5 2x - 3y = 7

Answer»


ANSWER :CONSISTENT
Discussion
1840.

find the value of x in the polynomial 2a^2+2xa+5a+10 if (a+x) is one of it's factors.

Answer»
Discussion
1841.

Numbers in each series follow some rule. Find the missing term. 1, 8, 9, 64, 25, 216, 49, ?

Answer»

496
504
512
532

Answer :B
Discussion
1842.

There are 25 disc numbered 1 to 25. They are put in a closed box and shaken throughly. A disc is drawn at random from the box. Find the probability that the number on the disc is : (i) an odd number (ii) divisible by 2 and 3 both (iii) a number less than 16.

Answer»


ANSWER :(i) `(13)/(25)` (II) `(4)/(25)` (III) `(3)/(5)`
Discussion
1843.

In the inequation2+ ( 3x-1)/( 5) le (2x- 1)/( 4)+ 3,write the greatestvalue of x, when x is a naturalnumber

Answer»


ANSWER :9.5
Discussion
1844.

If the 3^(rd) and the 9^(th) terms of an AP are 4 and -8 respectively, which term of this AP is zero ?

Answer»


ANSWER :5
Discussion
1845.

A mobile phone-based taxi service a base fee of $2 plus an amount per mile for thetrip. Ariel is charged $16.94 for a ride that takes 14 minutes and travels 10 miles. Victoria is charged $11.30 for ride that take 10 minutes and travels 6 miles. Q. What would be the carge for a ride that takes 8 minutes and travels 5 miles?

Answer»


ANSWER :`9.68`
Discussion
1846.

When x^3+2x^2-kx+4 . is divided by x - 2. the remainder is k. Find the value of constant k.

Answer»


ANSWER :`6 2/3`
Discussion
1847.

Find the reflection of the point Q(2,1) in the line y + 3= 0

Answer»


ANSWER :Q'(2,-7)
Discussion
1848.

Two players Sangeets and Reshma play a tennis match. It is known that the probability of Sangeets winning the match is 0.62. What is the probabilty of Reshma winning the match?

Answer»


ANSWER :(i) `3/8` (II) `5/8`
Discussion
1849.

Solve the following quatratic equation : a^(2)b^(2)x^(2)+b^(2)x-a^(2)x-1=0

Answer»

`(-1)/(a)and(1)/(b)`
`(-1)/(a^(2))and(1)/(b^(2))`
`(1)/(a^(2))and(1)/(b^(2))`
`(-1)/(a^(2))and(-1)/(b^(2))`

SOLUTION :Given equation is `a^(2)b^(2)X^(2)+b^(2)x-a^(2)x-1=0`
`impliesb^(2)x(x+1)-1)(a^(2)x+1)=0`
`IMPLIES(a^(2)x+1)(b^(2)x-1)=0`
`impliesa^(2)x+1=0orb^(2)x-1=0`
when `a^(2)x+1=0impliesx=-(1)/a^(2)` and `b^(2)x-1=0+impliesx=(1)/b^(2)`
HENCE, `-(1)/(a^(2))and(1)/(b^(2))` are roots of the equation.
Discussion
1850.

The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take pi=3.14)

Answer»


ANSWER :10 CM and 26 cm
Discussion