InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5101. |
A company manufacturers two types of novelty suouvenirs made of plywood. Souvenirsof type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit? |
Answer» Solution :Let `x` be the souvenirs of A type and `y` of B type be manufacture by the company. Then, 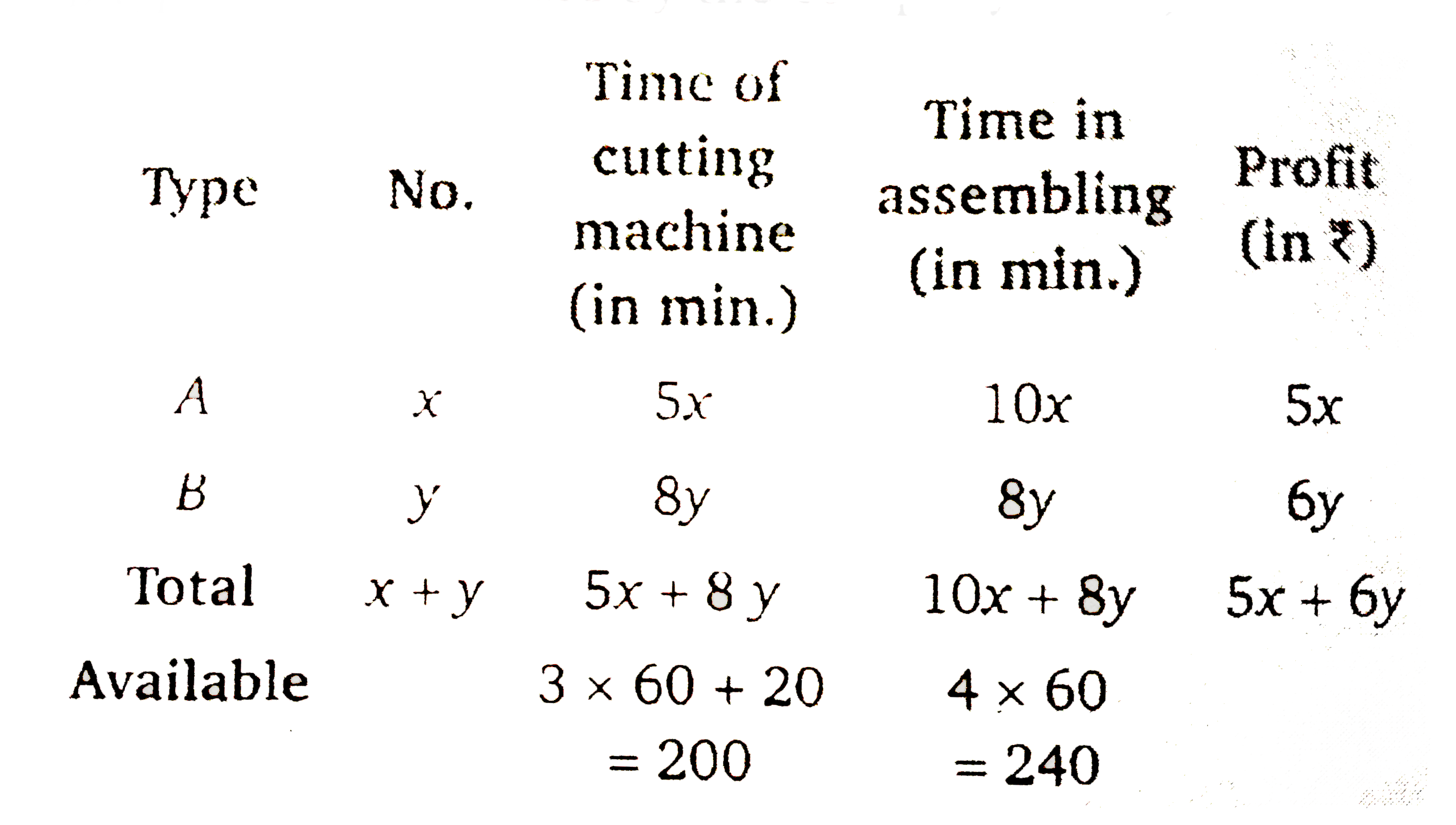 Maximise `Z=5x+6y`……………1 Constraints `5x+8yle200`………………2 `10x+8yle240implies4x+4yle120`………….3 `xge0,yge0`.................4 First, DRAW the graph of first line `5x+8y=200`.  PUT `(0,0)` in the inequation `5x+8yle200`, `5xx0+8xx0le200implies0le200`. (True) Therefore the half plane contains the ORIGIN. Since `x,yge0`.So the feasible region will be in first quadrant. Now, draw the graph of the line `5x+4y=120`. 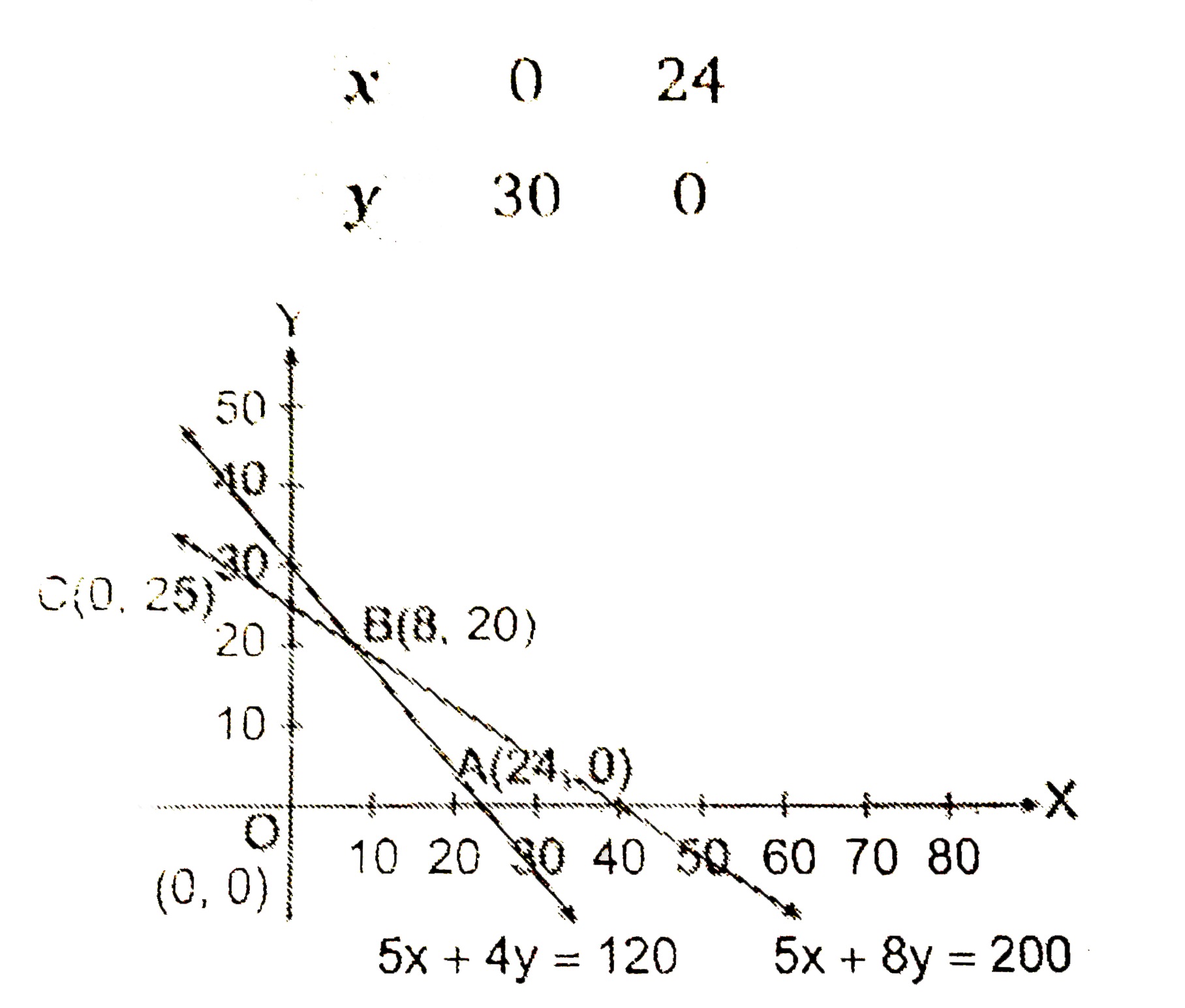 Put `(0,0)` in the inequation `5x+4yle120`, `5xx0+4xx0le120` `implies0le120` (True) Therefore, the half plane contains the origin. From equations `5x+8y=200` and `5x+4y=120`. The point of intersection is `B(8,20)`. `:.` Feasible region is OABCEO. Thus, the vertices of the feasible region are `O(0,0),A(24,0),B(8,20)` and `C(0,25)`. We FIND the value of `Z` at these vertices . 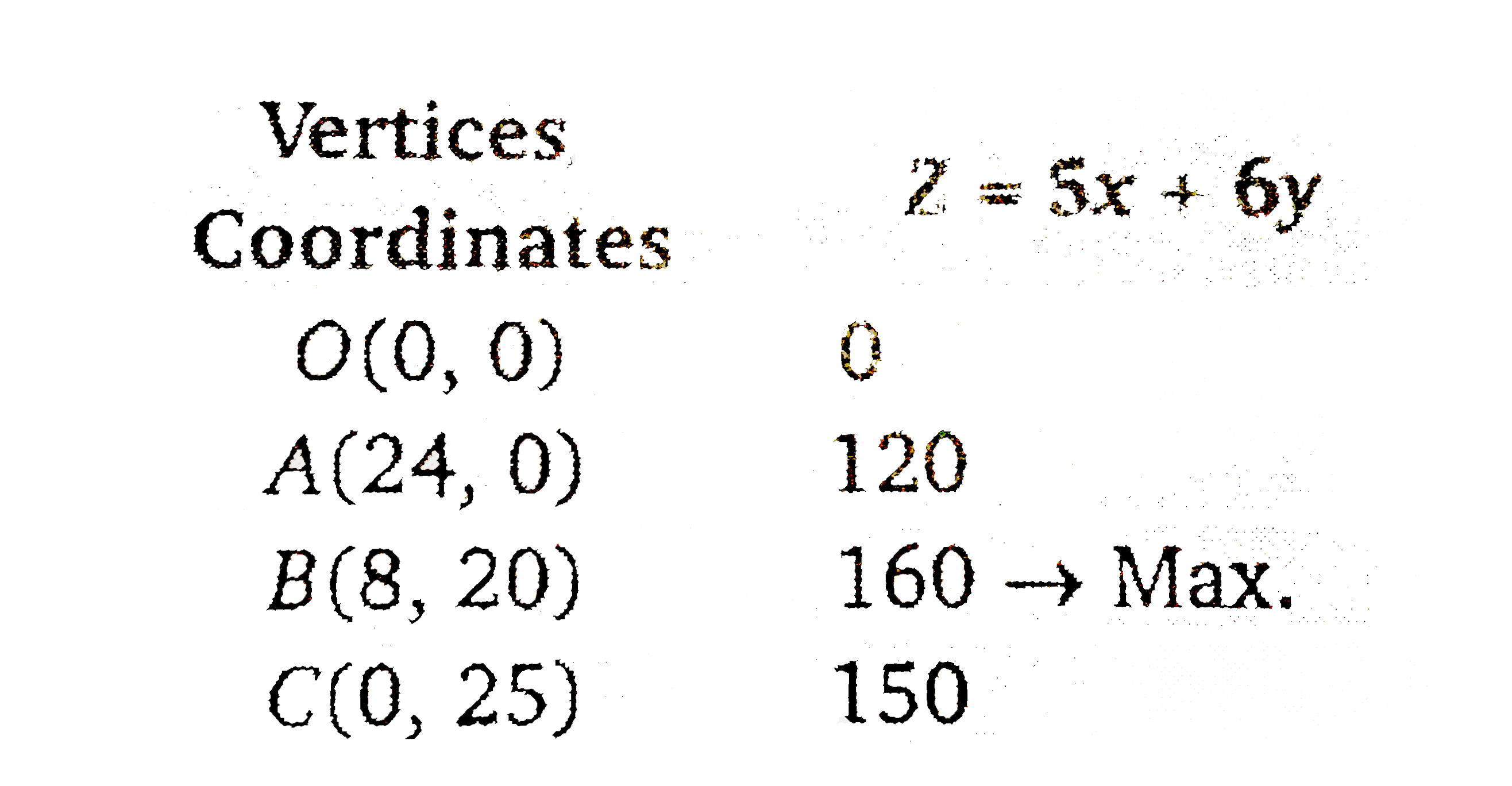 The maximum value of `Z` is Rs. 160 at point `B(8,20)`.Therefore, to obtain the maximum PROFIT Rs. 160 the souvenirs 8 of types of A and 20 of tyes B should be produced. |
|
| 5102. |
The equation of the locus of 2 such that |(z-i)/(z+i)|=2, where z = x + iy is a complex number , is |
|
Answer» `3X^(2) + 3Y^(2) + 10 y - 3 = 0` |
|
| 5103. |
If A'=[(-2,3),(1,2)] and B=[(-1,0),(1,2)] then find (A+2B)' |
|
Answer» |
|
| 5104. |
Let R be the set of all real number and f: [-1,1] to R is difined by f (x) = {{:( x sin "" (1)/( x ) "," , x ne 0 ), ( 0"," , x =0 ) :}. Then |
|
Answer» f satisfgies the conditions of ROLLE's theorem on `[-1,1]` |
|
| 5105. |
Compute P for n=11,r=0 |
|
Answer» SOLUTION :`n=11,r=0` `:.""^nP_r=""^11P_0=1` |
|
| 5106. |
If f(x) = cos x an g (x) = sin x then inta(logf(x))/((f(x))^(2))dx |
|
Answer» `f(x)(logf(x)+1)+x+C` |
|
| 5107. |
Two cards are drawn from the well shuffled pack of 52 playing cards with replacement. Find mean and standard deviation of the number of queens. |
|
Answer» |
|
| 5108. |
If Integration using rigonometric identities : int (cos 4x+1)/(cot x-tan x)dx=A cos 4x+c then A=.... |
|
Answer» `-(1)/(2)` |
|
| 5109. |
If a is perpendicular to b and c, |a|=2, |b|=3, |c|=4 and the angle between b and c is (2pi)/3, then [(a, b, c)] is equal to |
|
Answer» `4sqrt(3)` ` =|b||c| sin(2pi)/(3)A(.HATN)` `=|b||c|sin""(2pi)/3|a||hatn|cos60^@` `=|a||b||c|(sin(2pi)/3)` `2xx3xx4xxsqrt3/2=12sqrt3` |
|
| 5110. |
Cards are drawn one by one with replacement from pack of cards until red card appears. Findthe probability of getting king card in last draw. |
|
Answer» |
|
| 5111. |
If int_(0)^(alpha)(dx)/(1-cos alpha cosx)=(A)/(sin alpha)+B(alpha ne 0), then possible values of A and B are |
|
Answer» `A=(pi)/(2), B=0` |
|
| 5112. |
A point P moves on x-y plane such that PS +PS' = 4 where S(K,0) and S'(-K,0), then which of the following is not true about the locus of P? |
|
Answer» ellipse if `K in (-2,2)` `:. PS + PS' gt SS'` `RARR K in (-2,2)` If PSS' is collinear, the pair of coincident lines `rarr K = +-2` If PSS' neither forms triangle nor collinear then empty set `rArr PS + PS^(1) lt SS^(1)` `rArr K in (-oo,-2) uu(2,oo)` |
|
| 5113. |
The volume of the parallelepiped whose edges are vec(OA)=2hat(i)-3hat(j),vec(OB)=hat(i)+hat(j)-hat(k),vec(OC)=3hat(i)-hat(k) is |
| Answer» Answer :B | |
| 5114. |
Let bara,barb and barc are three mutually perpendicular unit vectors and a unit vector barr satisfying the equation (barb times barc) times (barr times bara)+(barc times bara) times (barr times barb)+(bara-barb) times (barr -barc)=0 then barr is |
|
Answer» `1/sqrt3(bara+barb+barc)` |
|
| 5115. |
(1/(1!) +1/(2!) +1(3!) + .....oo) (1/(2!) +1/(3!) +1(4!)-1/(5!) .....oo) |
|
Answer» `1/e` |
|
| 5116. |
Evaluate : (i) int_(0)^(2pi) {sin(sinx)+sin(cosx)}dx , (ii) int_(0)^(pi) (dx)/(5+4cos2x) (iii) int_(pi//2)^(0)(2 lnsinx-ln sin2x)dx , (iv) int_(0)^(pi//2) (asinx+bcosx)/(sinx+cosx)dx , (v)int_(0)^(pi//2) (sinx-cosx)/((sinx+cosx)^(2))dx |
|
Answer» |
|
| 5117. |
If a set A has 12 elements. Find the number of subsets of A having 4 elements |
|
Answer» |
|
| 5118. |
Find the number of 5 letter words that can be formed using the letters of the word 'MIXTURE' which begin with an vowel when repetitions are allowed. |
|
Answer» |
|
| 5119. |
Let f (x) be a twice differentiable function defined on (-oo,oo) such that f (x) =f (2-x)and f '((1)/(2 )) =f' ((1)/(4))=0. Then The minimum number of values where f ''(x) vanishes on [0,2] is : |
|
Answer» 2 |
|
| 5120. |
If numberof pointsofthefunctionf(x) =[2+10sin x],i nx in[0,(pi)/(2)] is sameas numberof points of non- differentiablity of the functiong(x)=(x-1)xx(x-2)|(x-1)(x-2). . .(x-2m(|,(m in N) i nin (-oo,oo) ,thenthevalueof m is |
|
Answer» 4 |
|
| 5121. |
The position vector of a point R which divides the line joining P(6, 3, -2) and Q(3, 1, -4) in the ratio 2 : 1 externally is |
|
Answer» `hat(i)+3HAT(J)-2HAT(k)` |
|
| 5122. |
Consider the following two statements: P : If 7 is an odd number, then 7 is divisible by 2. Q : If 7is a prime number, then 7 is an odd number. IfV_(1) is the truth value of the contrapositive of P and V_(2) is the truth value of contrapositive of Q then the ordered pair (V_(1),V_(2)) equals: |
|
Answer» `(F,F)` Truth value of Qand its contrapositive isT. |
|
| 5123. |
Let f (x) be a twice differentiable function defined on (-oo,oo) such that f (x) =f (2-x)and f '((1)/(2 )) =f' ((1)/(4))=0. Then int _(0) ^(1) f (1-t ) e ^(-cos pit) dt - int _(1) ^(2) f (2-t) e ^(cos pit) dtis equal to : |
| Answer» Answer :A | |
| 5125. |
Prove that the line joining two points of an ellipse the difference of whose eccentric angles is constant touches a fixed ellipse |
|
Answer» |
|
| 5126. |
If p is a prime, then sum of log_(p)p^(1//2)-log_(p)p^(1//3)+log_(p)p^(1//4)-……= |
|
Answer» `1+log2` |
|
| 5127. |
A oil company requires 12000, 20000 and 15000 barrels of high grade, medium grade and low grade oil respectively. Refinery A produces 100, 300 and 200 barrels per day of high, medium and low grade oil respectively whereas the refinery B produces 200, 400 and 100 barrels per day respectively. If A costs 400 per day and B cost 300 per day to operate. To find how many days should each be run to minimize the cost of requirement, formulate this as a L.P.P. |
|
Answer» Subject to the constraints : ` "" {:( x+2y ge 120 ),(3x+ 4y ge200),(2x+ yge150 ),(x ge 0 y ge 0):}` |
|
| 5128. |
Examine the function f(x)=2x^(2)-5 for its continuity at the point x = 3. |
|
Answer» |
|
| 5129. |
A and B throw a dice alternately til any one gets a 6 on the and win the game. If A begins the game find the probabilities of winning the game. |
|
Answer» |
|
| 5130. |
LetA={x inZ : 0lele 12}. showthat R={(a,b):|a-b| isa multipleof 4 is (i)reflexive, (ii)symmetric and (iii)transitive. Findthe setof elementsrelatedto 1. |
|
Answer» Solution :Clearly,`A={0,1,2,3,4. . .,10,11,12}.` here,R satisfiesthefollowingproperties . (i) Reflexivity Leta be anarbitrary elementof A , then , a-a =0, whichis a multipleof 4 .`THEREFORE ` a R a for all ` a in A.` (ii)SYMMETRY Leta R b , then `a R bimplies |a-b|` is a maultipleof 4 `implies |-(a-b)` is a multipleof 4 . `implies|b-a| ` ismultipleof4 `implies bR a.` `therefore` R issymmetric . (iii)tranistivity Leta R band b Rc . then , a R b, b R c `implies |a-b|` isa multipleof 4and|b-c| ismultipleof 4 . `Let |a-b|=4k_(1)and |b-c|=4k_(2).` the N , `|a-c|=|(a-b)-(b-c)|=|4k_(1)-4k_(2)|` `=|4(k_(1)-k_(2))|=4|K_(1) -K_(2)|` whichis a multipleof 4 `thereforea R b,b R c implies aRc . so ` R istransitive . thus,R is reflexive, symmetricand TRANSITIVE . `Now,[1] ={x in A :x R 1}.` `={ x in A : |x-1|` isa multipleof 4} `={1,5,9}.` HENCE, therequiredsetis `{1,5,9}.` |
|
| 5131. |
If d/(dx)(tan^(-1)(2^(x+1)/(1-4^(x))))=a^(x+1)/(1+b^(x))loga, find the value of a and b. |
|
Answer» |
|
| 5133. |
A(-1, 2, 3), B(1, 1, 1) and C(2, -1, 3) are three points in the plane. The unit vector perpendicular to the plane ABC is ………….. |
|
Answer» `+-((2hati+2hatj+hatk)/(3))` |
|
| 5134. |
Let ABCD be a cyclic quadrilateral such that AB=2, BC=3, angle B =120^(@) and area of quadrilateral =4sqrt3. Which of the following is/are correct ? |
|
Answer» The VALUE of `(AC)^(2)` is equal to 19 |
|
| 5135. |
Let ** be a binary operation on the set Q of rational numbers as followsa**b=a^2+b^2. Is the binary operation commutative and associative ? |
|
Answer» SOLUTION :`a**B=a^2+b^2` `=b^2+a^2=b**a` `a,b in Q` `THEREFORE **` is COMMUTATIVE |
|
| 5137. |
Evaluate the following integrals inte^(x)(tanx+logsecx)dx |
|
Answer» |
|
| 5139. |
For two independent events A and B, which of the following pair of events need not be independent ? a)A^',B^' b)A,B^' c)A^',B d)A-B,B-A |
|
Answer» `A^',B^'` |
|
| 5140. |
The solution of log((dy)/(dx)) = ax + by is |
|
Answer» `B E^(AX) + a e^(-by) = C` |
|
| 5141. |
A school has 3 freshmen for every 4 sophomores and 5 sophomores for every 4 juniors. If there are 240 juniors in the school, how many freshmen are there? |
|
Answer» |
|
| 5142. |
r_1, r_2are the radii of two non intersecting circles having A , B as centres. If 'P' is the mid- point of AB ,then the perpendicular distance of P from their radical axis is |
|
Answer» ` |( r_1^(2) -r_2^(2))/( 2AB) | ` |
|
| 5143. |
Letvec(a) = xhat(i) + 3hat(j) and = (x – 1)hat(i) – 2hat(j) and angle between vec(a) and vec(b) is obtuse then number of possible integral values of x is |
|
Answer» `implies x^(2) - x - 6 lt 0` `implies (x-3) (x+2) lt 0` `implies x in (-2, 3)`. |
|
| 5144. |
In the value circuit, C=(sqrt(3))/(2)muF,R_2=20omega, L=sqrt(3)/(10)H, and R_1=10omega .Current in L-R_1 pathsis I_1 and in C-R_2 path it is I_2. The voltage of A.C source is given by, V=200sqrt(2)sin(100t) volts. The phase difference between I_2 and I_2 is : |
| Answer» Solution :NA | |
| 5146. |
Solve 27x^3+42x^2-28x-8=0 given that its roots are in geometric progressive. |
|
Answer» |
|
| 5147. |
If the sum of all the binomial coefficients in (x+y)^n is 512 , then the greatest binomial coefficient is |
|
Answer» `""^10C_5` |
|
| 5148. |
Compound A(C_7H_8O)is insoluble in water, dilute HCl & aqueous NaHCO_3, it dissolves in dilute NaOH.When A is treatedwith Br_2 water it is converted into a compound C_7H_5OBr_3 rapidly. The structure ofA is |
|
Answer»
|
|
| 5149. |
If A={1,2,3},B={1,4,6,9} and R is a relation from A to B defined by 'x is greater than y'. The range of R is |
|
Answer» {1, 4, 6, 9} |
|
| 5150. |
e^(log(cosh^(-1)(2))) is equal to |
|
Answer» `log (2 - SQRT(3))` |
|