InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5801. |
Let f:R^(+)to R be a differentiable function satisfyingf(x) f(x)=e+(1-x)ln((x)/(e ))+int_(1)^(x)f(t)dt AA x in R^(+). If the area enclosed by the curve g(x)=x[f(x)-e^(x)] lying in the fourth quadrant is A, then find the value ofA^(-2). |
|
Answer» |
|
| 5802. |
Let f(x)={{:(x+2","-1lexlt0),(1","x=0),((x)/(2)","0lt x le1):}. Then on [-1,1], this function has : |
|
Answer» a minimum |
|
| 5803. |
An eight digit number divisible by 9 is to be formed using digits from 0 to 9 without repeating the digits. Thenumber of ways in which this can be done is |
|
Answer» `72 (7!)` |
|
| 5804. |
The minimum value of |z-1|z-5| is |
|
Answer» 5 |
|
| 5806. |
Where n is some integer then answer the following question The value of n is |
|
Answer» 0 |
|
| 5807. |
Show that int [ (1 + nx^(n-1) - x^(2n))/((1 - x^(n)) sqrt(1 - x^(2n)) ) ]e^(x) dx = e^(x) sqrt((1 + x^(n))/(1 -x^(n))) + c |
|
Answer» |
|
| 5808. |
If p(x) = ax^2 + bx + c and Q(x) = -ax^2 + dx +c where ac ne 0 then p(x). Q(x) = 0 has at least …………. Real roots |
| Answer» Answer :C | |
| 5809. |
int_(2)^(5) sqrt((x-2)/(5-x))dx= |
|
Answer» `(3PI)/(4)` |
|
| 5810. |
Find the number of 4 xx 4 array where entries are from the set {0,1,2,3} and which are such that the sum of the numbers in each of the four rows and in each of the four columns is divisible by 4. |
|
Answer» |
|
| 5811. |
Let ** be a binary defined on R by a**b=(a+b)/(4)AAa,binR then the operation ** is |
|
Answer» a.COMMUTATIVE and ASSOCIATIVE |
|
| 5812. |
A square of side a lies above the x-axis and has one vertex at the origin. The side passing through the origin makes and angle alpha (0 lt alpha lt (pi)/(4)) with the positive direction of x-axis. The equation of its diagonal not passing through the origin is |
|
Answer» `y(COS alpha+SIN alpha)+X(sin alpha-cos alpha)=a` |
|
| 5813. |
If a,b,c and A,B,C inR-{0} such that aA+bB+cD+ sqrt((a^(2)+b^(2)+c^(2))(A^(2)+B^(2)+C^(2)))=0, then value of (aB)/(bA) +(bC)/(cB) + (cA)/(aC) is |
|
Answer» 3 `therefore costheta=(veca.(vecb+vecc))/(|veca||vecb+vecc|)` `=(2cosalpha)/sqrt(2+2cosalpha) = (cosalpha)/(cosalpha/2)` `therefore theta=cos^(-1)(cosalpha)/(cosalpha/2)` `therefore vecr_(1)vecr_(2)-|vecr_(1)||vecr_(2)|` `rArr vecr_(1)` and `vecr_(2)` are anti-parallel `rArr a/A=b/B=c/C=k` where k is any constant `rArr (aB)/(bA) +(bC)/(cB) + (cA)/(aC)=3` |
|
| 5814. |
Draw the graph of y=e^(x)+e^(-2x) |
|
Answer» Solution :We have `y=f(x)=e^(x)+e^(-2x)` Clearly, the doamin of the function is R. `f(0) =1+1=2` ALSO `f(x) gt 0, AA x in R` `f^(')(x) = e^(x)-2e^(-x)= e^(-2x)e^(3x-2)` `f^(')(x)=0 therefore e^(3x)=2` or `x=1/3log2` `f(1/3log2) e^(1/3log2) + e^(-2/3)log2=2^(1//3) + 2^(-2//3) = 3/2^(2/3)` `f(x)` DECREASES in `(-INFTY, 1/3 log2)` and increases in `(1/3log2, infty)` Hence the graph of the function is as shown in the following figure. 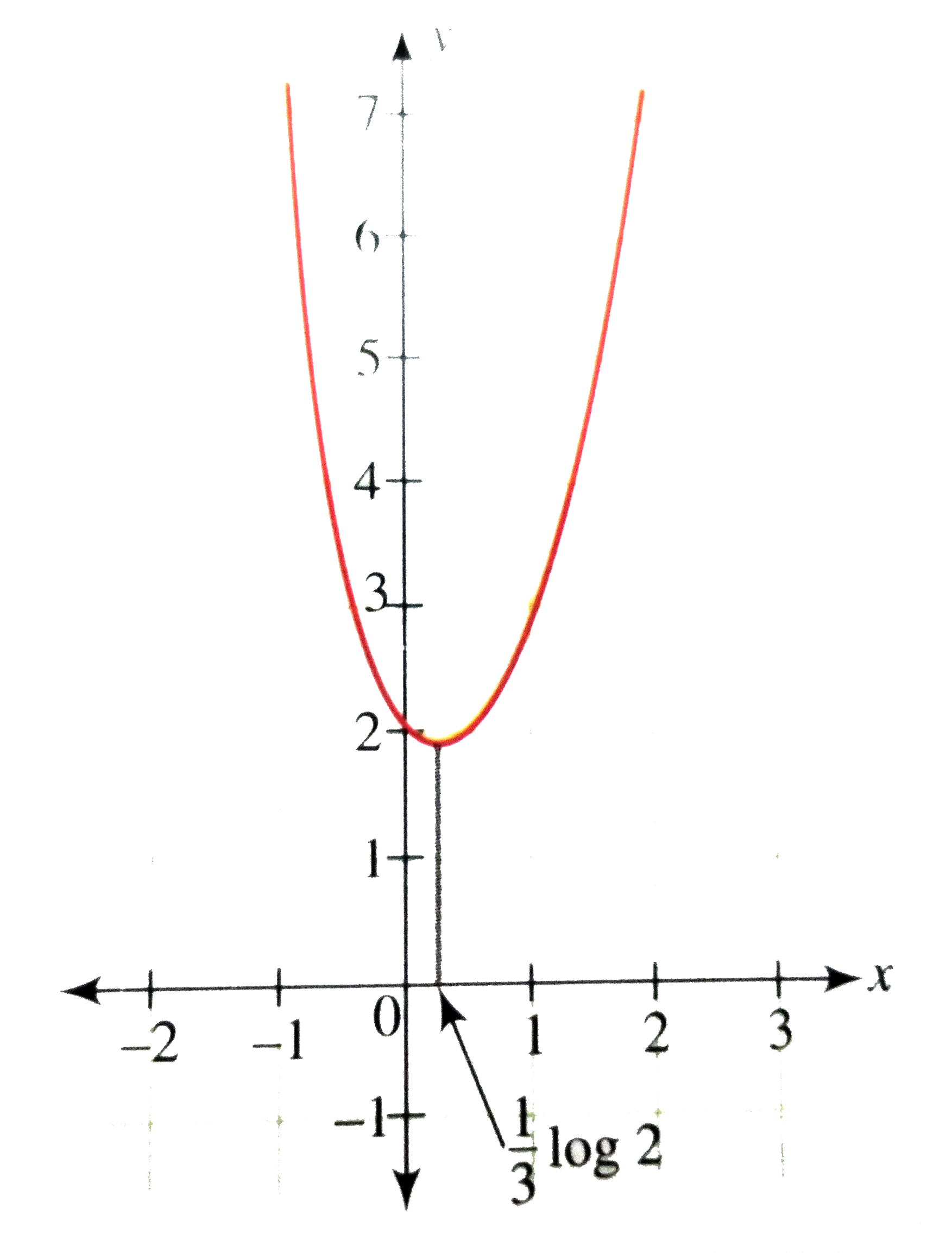
|
|
| 5815. |
Find the mean deviation about the median for the data |
|
Answer» |
|
| 5816. |
If the circles x^2+y^2+2x+2ky+6=0 and x^2+y^2+2ky+k=0 intersect orthogonally,show that k=2 or -3/2 |
|
Answer» 4 |
|
| 5817. |
If r a=r. b=r. c=1 where a, b, c are any three non-coplanar vectors, then r is |
|
Answer» coplanar with a, b, c `implies r((a-b)=0` Similarly, `r*(b-c)=0` Since, r is parallel to `(a-b)xx(b-c).` So, r is parallel to `axx b +c xx a +b xx c` |
|
| 5818. |
Moist skin help in respiration in :- |
| Answer» Answer :A | |
| 5820. |
Given that one root of 2x^3+3x^2-8x+3=0is double of another root , find the roots of the equation. |
|
Answer» |
|
| 5821. |
The sum of the infinite series cot^(-1)2 + cot^(-1)8 + cot^(-1)18 + cot^(-1) 32 +..... is equal to |
|
Answer» `pi//3` |
|
| 5822. |
Evaluate the following determinants. [[1,1,1],[2,2,2],[3,3,3]] |
| Answer» SOLUTION :`[[1,1,1],[2,2,2],[3,3,3]]=0(because C_1=C_2)` | |
| 5823. |
Out of the first 25 natural numbers two are chosen at random. The probability for one of the numbers to be a multiple of 3 and the other to be a multiple of 5 is |
|
Answer» `1//15` |
|
| 5824. |
Write the value of intx^20sec^2x dx-intx^20tan^2x dx. |
| Answer» SOLUTION :`intx^20sec^2dx-intx^20tan^2dx=intx^20(sec^2x-tan^2x0dx=intx^20dx=int(x^21)/21+c` | |
| 5825. |
If 2cosx+2cos3x=cosy and 2sinx+2sin3x=siny then cos 2x= |
|
Answer» `-7//8` |
|
| 5826. |
The radius of a circle is increasing uniformly at the ratio 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm. |
|
Answer» |
|
| 5828. |
The solution of (dy)/(dx) = 1 -x(y-x) - x^(3) (y-x)^(3) is |
|
Answer» `(y -x)^(2) (x^(2) + 1 + CX^(2)) =1` |
|
| 5829. |
For any two vectors bara,barb prove that |bara xx barb|^2 = |bara|^2|barb|^2 - (bara.barb)^2. |
|
Answer» |
|
| 5831. |
Find the area of the region enclosed by the given curves . x=4-y^(2), x=0 |
|
Answer» |
|
| 5832. |
If A and B are two finite sets such that the total number of subsets of A is 960 more the total number of subsets of B, then n(A) -n(B) is equal to . |
|
Answer» 2 |
|
| 5833. |
If the functionf(x) = 1/(x+2),then find the points of discountinuity of the composite functiony = f{f(x)}. |
|
Answer» `:. y =f{f(x)}` ` = f((1)/(x+2)) = (1)/((1)/(x+2)+2)` `= (1)/(1+2x+4).(x+2)= ((x+2))/((2x+5))` So,the functiony will not continousat those points, whereit is not denfined as it is a RATIONALFUNCTION. THEREFORE, `y = (x+2)/((2x+5))` is not defined, when `2x + 5 = 0` `:.x = (-5)/(2)` Hence,y isdiscountinuousat `x= (-5)/(2)` |
|
| 5834. |
Let alpha = 3 cos^(-1) (5/sqrt28) + 3 tan^(-1) ( sqrt3/2) " and " beta = 4 sin ^(-1) ((7sqrt2)/10) - 4 tan^(-1) (3/4), then which of the following does not hold (s) good ? |
|
Answer» `ALPHA LT PI " but " beta gt pi` |
|
| 5835. |
Integration using rigonometric identities : int ((sin theta+cos theta))/(sqrt(sin2 theta))d theta=..... |
|
Answer» `log|cos theta- SIN theta+ sqrt(SIN2 theta)|` |
|
| 5836. |
Find the equation of parabola whose axis is parallel tox-axis and which passes through the points (-2, I) (1,2) (-1. 3) |
|
Answer» |
|
| 5837. |
If int (sqrt3)/(sqrtx- root 3x) dx =x + Ex ^(5//6) + Dx ^(1//2) + Bx ^(1//3) + Ax^(1//6)+ log (root6x-1)^(6) +K, then A +B+C+D+E= |
|
Answer» `137/10` |
|
| 5838. |
Find the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y= 12-x^2 |
|
Answer» |
|
| 5839. |
Find the scalar and vector projection of veca on vecb. veca = hati+hatj,vecb = hatj+hatk |
|
Answer» SOLUTION :Scalar PROJECTION of `veca` on `vecb` = `(veca.vecb)/|vecb| = ((hati+hatj).(hatj+hatk))/_hatj+hatk| = 1/sqrt2` Vector projection of `veca` on `vecb` = `((veca.vecb)/|vecb|) vecb/|vecb| = 1/sqrt2 (hatj+hatk)/sqrt2 = hatj+hatk/2` |
|
| 5840. |
The sum of the series1/1.3+2/1.3.5+3/1.3.5.7+…is equal to : |
|
Answer» Twice MAXIMUM value of`F(x)=x-x^2` |
|
| 5841. |
int_(0)^(pi//2) (5 tan x - 3 cotx)/(tan x + cot x) dx= |
| Answer» ANSWER :A | |
| 5842. |
If xgt0 and the range of 1, 2, x, 5, and x equals 7, what is the approximate average (mean) of the list ? |
|
Answer» |
|
| 5844. |
{:(,"List-I",,"List-II",),((P),"Let volume ofa tetrahedron ABCD is",(1),3,),(,(81)/(2) "cube unit and volume of parallelopiped",,,),(,"whose three coterminous edges are line",,,),(,"segment joining centroid of any face of ",,,),(,"tetrahedron with centroids of its other three",,,),(,"faces is V cubic unit. then V is",,,),((Q),"If images ofthe point (1,0,1) in the plane" ,(2),8,),(,x-y-z=1 "is (a,b,c) then 3(a-b+c)",,,),(,"is equal to",,,),((R),"Locus of all the points which are at a distance of",(3),3,),(,3 "units from the line" underset(r )(rarr)=lambda(i+j+k)" is given by",,,),(,x^(2)+y^(2)+z^(2)-xy-yz=(k)/(2) "then find"(k)/(9),,,),((S),underset(a)(rarr) "and" underset(b)(rarr)and underset(a)(rarr)underset(b)(rarr)underset(c)(rarr)"are such that" |underset(a)(rarr)|=sqrt(3)|underset(b)(rarr)|=2,(4),7,),(,"and" |underset(c)(rarr)=sqrt(6). "If"underset(a)(rarr)underset(b)(rarr)lt0underset(c)(rarr) "is perpendicular to both" ,,,),(,underset(a)(rarr) "and" underset(b)(rarr) "and" underset(a)(rarr)underset(b)(rarr)underset(c)(rarr) "form the coterminous edges of a",,,),(,"tetrahedron of unit volume then angle between" underset(a)(rarr) "and" underset(b)(rarr) ,,,),(,"is" (pi)/(q) "(where p,q are coprime number) where (p+q) is",,,):} |
|
Answer» <P>`{:(P,Q,R,S),(1,2,3,4):}` given volume of tetrahedron is |(1)/(6)[underset(a)(-)underset(b)(-)underset(c)(-)]|=(81)/(2)` |(underset(a)(-),underset(b)(-)underset(c)(-))|=3^(5)` Centroids by faces are ` G_(1)((vec(a)+vec(b) +vec(c))/(3))` ` G_(2)((vec(a)+vec(b))/(3))` G_(3)((vec(b)+vec(c))/(3))` `G_(4)((vec(c)+vec(a))/(3))` Volume of parallelopiped |vec(G_(1)G_(2))vec(G_(1)G_(3))vec(G_(1)G_(4))]|` =|[-vec(c)/(3)-vec(a)/(3)-vec(b)/(3)]|[[vec(a)vec(b)vec(c)]]/(3^(3))|=9` (Q) Let the image of the point (1,0,1) in the plane x-y-z=1 is A (a,b,c)` D.R. of AA are `(a-1,b,c-1)` D.R. of normal are `(1,-1,-1)` `(a-1)/(1)=(b)/(-1)=(c-1)/(-1)=lambda` `impliesa=lambda+1, b=-lambda, c=1-lambda` mid point of AA' lie on plane `x-y-z =1 implies lambda=(2)/(3)` `a=(5)/(3), b=(-2)/(3),c=(1)/(3) implies 3(a+b+c)=3((8)/(3))=8` (R) `vec(QP).(i+j+k)=0` implies (x-lambda)+(y-lambda)+(z-lambda)=0` lambda=(x+y+z)/(3)` 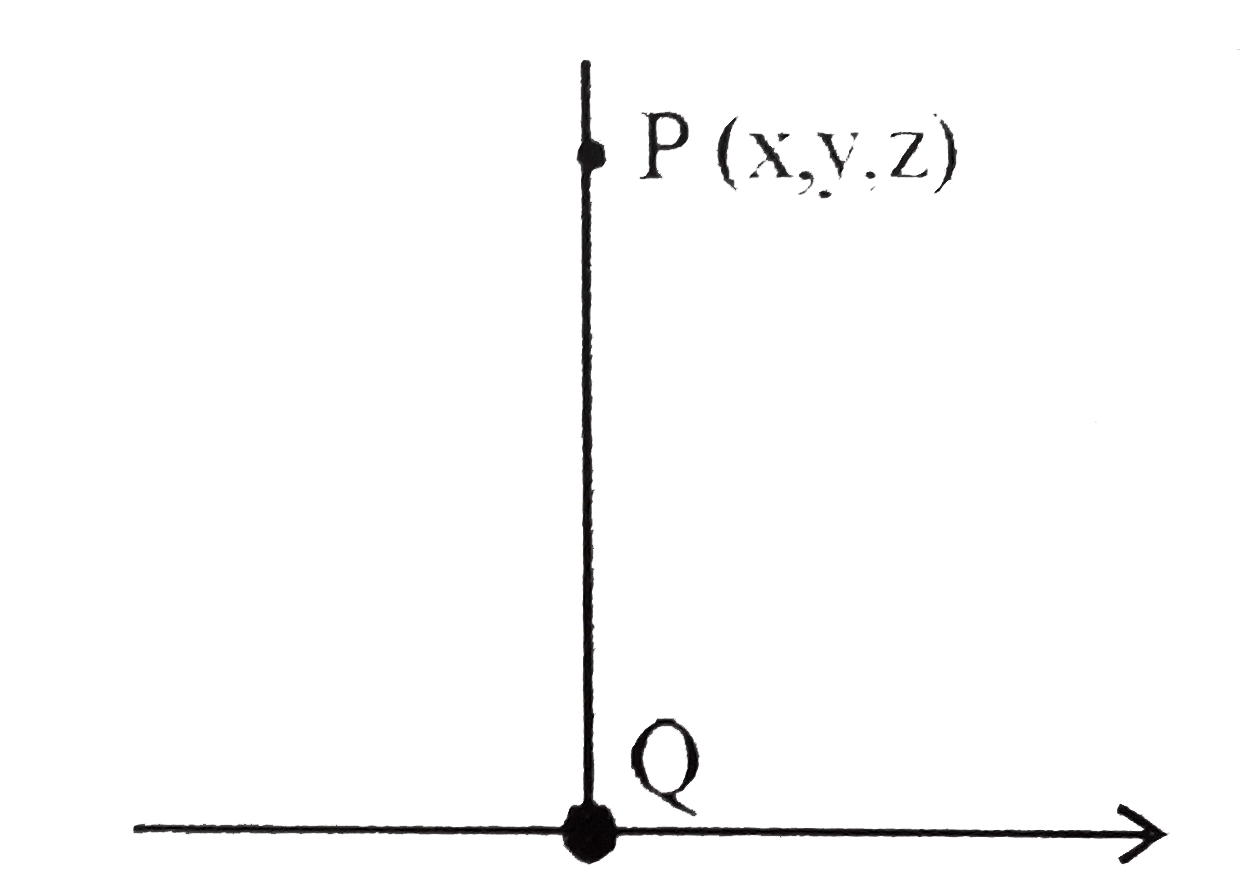 `(PQ)^(2)=9implies (x-lambda)^(2)+(y-lambda)^(2)+(z-lambda)^(2)=9` x^(2)+y^(2)+z^(2)+3lambda^(2)-2lambda(x+y+z)=9` `x^(2)+y^(2)+z^(2)+3lambda^(2)-2lambda.3lambda=9` implies x^(2)+y^(2)+z^(2)-3((x+y+z)/(3))^(2)=9` implies x^(2) +y^(2)+z^(2)-xy-yz-zx=(27)/(2)` `k=27, (k)/(9)=3` (S) underset(C)(rarr)=lambda(underset(a)(-)xxunderset(b)(-)) also` |(1)/(6)[underset(a)(-)underset(b)(-)underset(c)(-)]|=1implies |[underset(a)(-)underset(b)(-)underset(c)(-)]|=6` implies |vec((a)(-)xxvec(b)(-))vec(c)(-)|=6implies|c|^(2)/|lambda|=6` implies 6=6|lambda|implies|lambda|=1` `implies|vec((a)(-)xxvec(b)(-)).vec(c)(-)|=6implies(|c|^(2))/(|lambda|)=6` `implies 6 = 6|lambda|implies |lambda|=1` `therefore |c|^(2)=lambda^(2)|a|^(2)|b|^(2) sin^(2)THETA` `implies 6=12sin^(2)theta=theta=(3pi)/(4)(a.blt0)` `p+q=7` |
|
| 5845. |
The reflection point of the point(0, 3,-2)" on the line "(1-x)/( 2)= 2 -y=z + 1is |
|
Answer» ` ( 1,2,-1)` |
|
| 5846. |
A point P moves such that sum of the slopes of the normals drawnfrom it to the hyperbola xy=16 is equal to the sum of the ordinatesof the feet of the normals. Let 'P' lies on the curve C, then : Q.Area of the equilateral triangle, inscribed in the curve C, and having one vertex same as the vertex of C is : |
| Answer» Answer :A | |
| 5847. |
A point P moves such that sum of the slopes of the normals drawnfrom it to the hyperbola xy=16 is equal to the sum of the ordinatesof the feet of the normals. Let 'P' lies on the curve C, then : Q. The equation of 'C' is : |
| Answer» Answer :B | |
| 5848. |
A point P moves such that sum of the slopes of the normals drawnfrom it to the hyperbola xy=16 is equal to the sum of the ordinatesof the feet of the normals. Let 'P' lies on the curve C, then : Q. If tangents are drawn to the curve C, then the locus of the midpoint of the portion of tangent intercepted between the co-ordinate axes, is : |
|
Answer» `X^(2)=4y` |
|
| 5849. |
If n is an integer with 0le n le 11, then the minimum value of n!(11 - n)! is attained when a value of n equals to |
|
Answer» 11 |
|
| 5850. |
If the graph of the antiderivative F(x) of f(x) = log(log x) + (log x) - 2 passes through (e,7-e) then the term independent of x in F(x) is |
|
Answer» |
|