InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5901. |
{:(" "Lt),(n rarr oo):} ((1)/(sqrt(n^(2)))+(1)/(sqrt(n^(2)+n))+(1)/(sqrt(n^(2)+2n))+(1)/(sqrt(n^(2)+3n))+....(1)/(sqrt(n^(2)+n(n-1)))))= |
|
Answer» `2 SQRT(2)` |
|
| 5902. |
If p,q, in rand p^2+q^2-pq-q+1 le 0 + alpha + beta + gamma = 0 , then |(1,cosy,cosbeta),(cosgamma,p,cosalpha),(cosbeta,cosalpha,q)|= |
|
Answer» 1 |
|
| 5903. |
If [[1,-x],[4,-3]] =[[1,8],[4,-3]] then value of x is : |
|
Answer» 8 |
|
| 5904. |
A fair dice is rolled 6 times. If "getting an even number" is a success the probability of 5 successes is ………….. |
| Answer» Answer :B | |
| 5905. |
There are 3 rows containing 2 seats in each row. In how many ways 3 persons can be seated such that no row remains empty. |
|
Answer» |
|
| 5906. |
If a set A has 12 elements. Find the number of subsets of A having atmost 3 elements |
|
Answer» |
|
| 5907. |
Solve the following Linear Programming Problems graphically : Minimise Z = x + 2y subject to 2x+y ge 3, x+2y ge 6, x, y ge 0 |
|
Answer» |
|
| 5908. |
Find the number of ordered triples (a,b,c) of positive integers such that abc= 108 |
|
Answer» |
|
| 5909. |
2x-y+3z=1 3x-2y+5z=-4 5x-4y+9z=14 |
| Answer» | |
| 5910. |
Find maximum and minimum value of the following functions in the given interval.f(x)=x^(2)log x, x in [0, 2] |
|
Answer» Minimum value 0 |
|
| 5911. |
Consider two regions R_(1):"points P are nearer to (1,0) than to "x=-1. R_(2): "Points P are nearer to (0,0) than to (8,0)" Find the area of the region common to R_(1) and R_(2). |
|
Answer» <P> `therefore""sqrt((x-1)^(2)+y^(2))lt|x+1|` `rArr""y^(2)lt4x` `rArr"point P lie inside parabola "y^(2)=4x` `R_(2) :` Points P(x,y) are nearer to (0,0) than to (8,0) `therefore""|x|lt|x-8|` `rArr""x^(2)LTX^(2)-16x+64` `rArr""xlt4` `rArr""`point P lie to the left side of line x=4 The AREA of common region of `R_(1) and R_(2)` is area bounded by x=4 and `y^(2)=4x.` 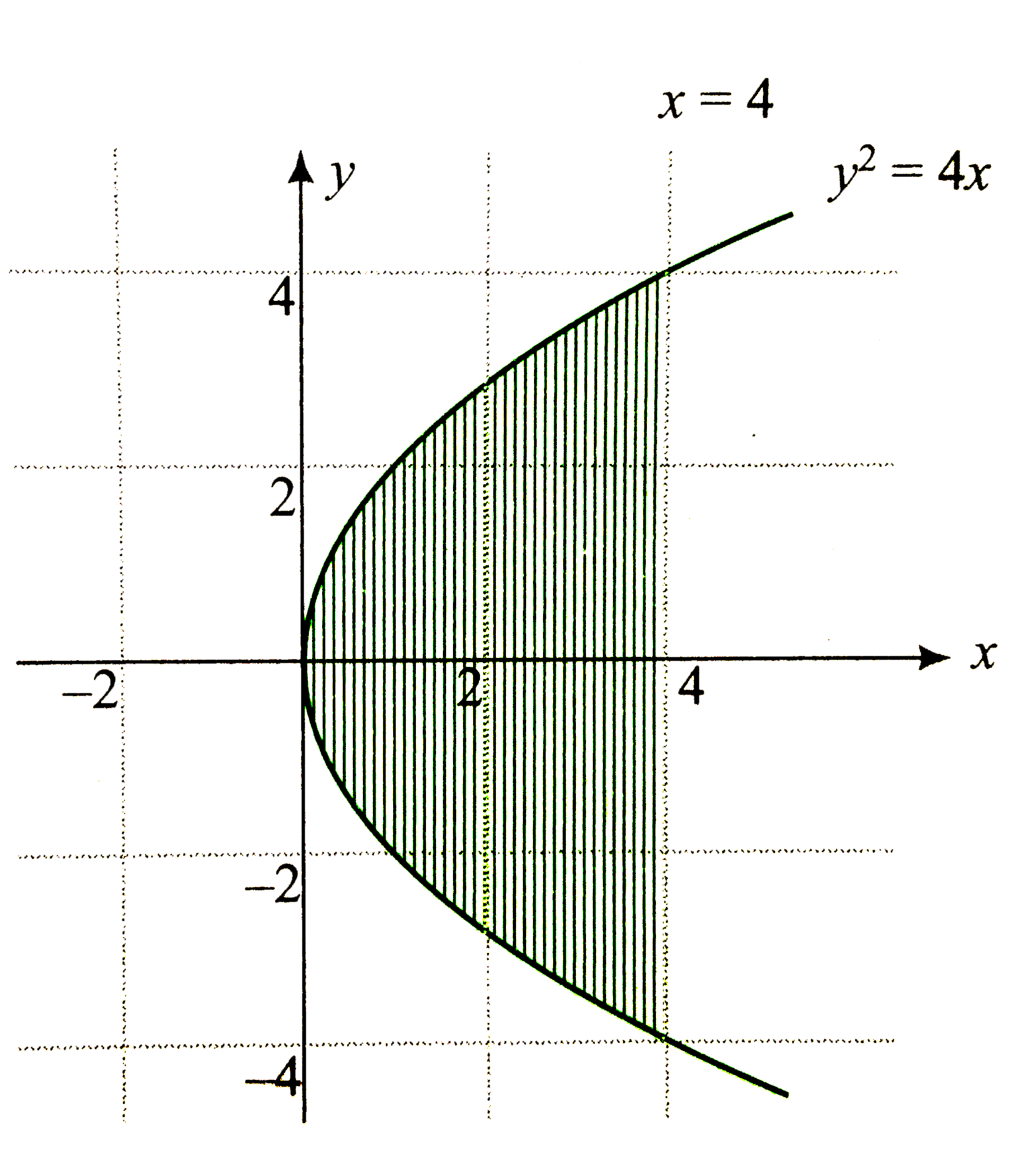 `therefore"Required area "=2overset(4)underset(0)int(4-(y^(2))/(4))dy` (Integrating along x-axis) `=2[4y-(y^(3))/(12)]_(0)^(4)` `=2[16-(64)/(12)]` `(64)/(3)` sq. units |
|
| 5912. |
"if "f(x) ={ underset(5x, 1,2 le x le 3)(3x+4, 0 le x le 2}}, then evaluate int_(0)^(3) f(x) dx. |
|
Answer» |
|
| 5913. |
There are 5 cards numbered 1 to 5, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on two cards drawn. Find the mean and variance of X. |
|
Answer» |
|
| 5914. |
The normal at 'P'cuts the axis of the parabola y^(2) =4ax in G and S is the focus of the parabola. IfDelta SPGis equilateral then each side is of length. |
|
Answer» a |
|
| 5915. |
Let O(0,0) , P(2,0) and Q (6,0) be the vertices of triangle OPQ . If R be a point inside the triangle OPQ such that areas of DeltaOPQ,DeltaPQRandDeltaOQRare equal , then the abscissa of R is - |
|
Answer» |
|
| 5916. |
The ratio of the number of chickens to the number of pigs to the number of horses on Richard's farm is 33:17 : 21. What fraction of the animals are either pigs or horses? |
|
Answer» `16//53` |
|
| 5917. |
If f: R to R , f(x) = (3x -5)/(4), then f^(-1) (x) is equal to |
|
Answer» `(5x-3)/(4)` |
|
| 5918. |
The vector, 2hat(i)+hat(j)+2hat(k),hat(i)+lambdahat(j)-hat(k)t" and "2hat(i)-lambdahat(k) areco-planar if |
|
Answer» `lambda=-2` |
|
| 5919. |
If z=((sqrt(3)+i)^(3)(3i+ 4)^(2))/((8+6i)^(2)), then |z| is equal to |
| Answer» ANSWER :B | |
| 5920. |
If a and b are positive integers such that b gt a then underset(n rarr oo)(lim) [(1)/(na) + (1)/(na + 1) + (1)/(na + 2) + ….+ (1)/(nb)]= |
|
Answer» `LOG ((B)/(a))` |
|
| 5921. |
Find the integrals of the functions (cos2x+2sin^(2)x)/(cos^(2)x) |
| Answer» Answer :C | |
| 5922. |
Two arithmetic progressions have the same numbers. The reatio of the last term of the first progression to the first term of the second progression is equal to the ratio of the last term of the second progression to the first term of first progression is equal to 4. The ratio of the sum of the n terms of the first progression to the sum of the n terms of teh first progression to the sum of the n terms of the second progerssion is equal to 2. |
|
Answer» `6//5` `(a+(n-1)d)/b=(b+(n-1)e)/a=4` (1) `(n/2[2a+(n-1)d])/(n/2[2B+(n-1)e])=2` (2) From (1) and (2), we get a-4b+(n-1)d=0 (3) b-4a+(n-1)e=0 (4) 2a-4b+(n-1)d-2(n-1)e=0 (5) `4xx(3)+(4)` gives `-15b+4(n-1)d+(n-1)e=0` (6) `(4)+2xx(5)` gives `-7b+2(n-1)d-3(n-1)e=0` (7) Further, `15xx(7)-7xx(6)` gives `2(n-1)d-52(n-1)e=0` or d=26e`(becausengt1)` `therefored//e=26` Putting d=26e in (3) and solving it with (4), we get a=2(n-1)e,b=7(n-1)e Then, the ratio of their `n^(th)` terms is `(2(n-1)+(n-1)26e)/(7(n-1)e+(n-1)e)=7/2` |
|
| 5923. |
Two arithmetic progressions have the same numbers. The reatio of the last term of the first progression to the first term of the second progression is equal to the ratio of the last term of the second progression to the first term of first progression is equal to 4. The ratio of the sum of the n terms of the first progression to the sum of the n terms of teh first progression to the sum of the n terms of the second progerssion is equal to 2. The ratio of their common difference is |
|
Answer» 12 `(a+(n-1)d)/b=(b+(n-1)e)/a=4` (1) `(n/2[2a+(n-1)d])/(n/2[2B+(n-1)e])=2` (2) From (1) and (2), we get a-4b+(n-1)d=0 (3) b-4a+(n-1)e=0 (4) 2a-4b+(n-1)d-2(n-1)e=0 (5) `4xx(3)+(4)` gives `-15b+4(n-1)d+(n-1)e=0` (6) `(4)+2xx(5)` gives `-7b+2(n-1)d-3(n-1)e=0` (7) Further, `15xx(7)-7xx(6)` gives `2(n-1)d-52(n-1)e=0` or d=26e`(becausengt1)` `therefored//e=26` Putting d=26e in (3) and solving it with (4), we get a=2(n-1)e,b=7(n-1)e Then, the ratio of their `n^(th)` terms is `(2(n-1)+(n-1)26e)/(7(n-1)e+(n-1)e)=7/2` |
|
| 5924. |
Two arithmetic progressions have the same numbers. The reatio of the last term of the first progression to the first term of the second progression is equal to the ratio of the last term of the second progression to the first term of first progression is equal to 4. The ratio of the sum of the n terms of the first progression to the sum of the n terms of teh first progression to the sum of the n terms of the second progerssion is equal to 2. The ratio of their first term is |
|
Answer» `2//7` `(a+(n-1)d)/b=(b+(n-1)e)/a=4` (1) `(n/2[2a+(n-1)d])/(n/2[2B+(n-1)e])=2` (2) From (1) and (2), we GET a-4b+(n-1)d=0 (3) b-4a+(n-1)e=0 (4) 2a-4b+(n-1)d-2(n-1)e=0 (5) `4xx(3)+(4)` GIVES `-15b+4(n-1)d+(n-1)e=0` (6) `(4)+2xx(5)` gives `-7b+2(n-1)d-3(n-1)e=0` (7) Further, `15xx(7)-7xx(6)` gives `2(n-1)d-52(n-1)e=0` or d=26e`(becausengt1)` `therefored//e=26` Putting d=26e in (3) and solving it with (4), we get a=2(n-1)e,b=7(n-1)e Then, the ratio of their `n^(th)` terms is `(2(n-1)+(n-1)26e)/(7(n-1)e+(n-1)e)=7/2` |
|
| 5925. |
Some standard forms of integration : intsqrt(x^(2)+7)dx=..........+C |
|
Answer» `(X)/(2)SQRT(x^(2)+7)+(7)/(2)log|x+sqrt(x^(2)+7)|` |
|
| 5926. |
If log_(e )k=2[(3)/(5)+(1)/(3)((3)/(5))^(3)+(1)/(5)((3)/(5))^(5)+….oo] then k = |
|
Answer» 2 |
|
| 5927. |
If a, b and c are roots of the equation x^3+qx^2+rx +s=0 then the value of r is |
|
Answer» 184 a+b+c=25 2a=b+2 `c^(2)=18b` Elminating a from (1) and (2), we have `b=16-(2c)/3` Then from (3), `c^(2)=18(16-(2c)/3)` or `c^(2)+12c-18xx16=0` or `(c-12)(c+24)=0` Now, c=-24 is not possible since it does not lie between 2 and 18. Hence, c=12. Then from (3), b=8 and finally from (2),a = 5. Thus, a=5,b=8 and c=12. Hence, abc`=5xx8xx12=480`. ALSO,equation `ax^(2)+bx+c=0 is 5x^(2)+8x+12=0`, which has imaginary ROOTS. If a,b,c are roots of the equation `x^(3)+QX^(2)+rx+s=0`, then the sum of PRODUCT of roots taken two at a time is `r=5xx8+5xx12+8xx12=196`. |
|
| 5928. |
Number of integral solutions of (x+2)/(x^2 + 1) gt 1/2 is |
|
Answer» 0 |
|
| 5929. |
Compute theintegrals I = int_(0)^(a) x^(2) sqrt((a - x)/( a + x)) dx, a gt 0 |
|
Answer» |
|
| 5930. |
Let f(x) = |x-2| AA x in R and g(x) =f(f(f(x))), then the number of solutions of g(x) = 3/2 is |
|
Answer» 4 |
|
| 5931. |
If the circlex^(2)+ y ^(2)+ ax + by - 12=0has the centre at (2,3)then find a, b and the radius of the circle . |
|
Answer» |
|
| 5932. |
If the vectors b, c, d are not coplanar, then the vector (axx b)xx(c xx d)+(a xx c)xx(d xx b)+(a xx d)xx(b xx c) is |
|
Answer» PARALLEL to a |
|
| 5933. |
If 1+x^(2)=sqrt(3)x, then sum_(n=1)^(24)(x^(n)-(1)/(x^n))^(2) is equal to |
| Answer» ANSWER :D | |
| 5934. |
Evaluate the following integrals (i) int_(1)^(2)((x+1)^(2))/(sqrt(x))dx |
|
Answer» |
|
| 5935. |
Sketch the graphs of the following functions. f(x) = 1 + 1/x^2 |
Answer» SOLUTION :
|
|
| 5936. |
Using binomial distribution find the mean and variance of X forthe following experiments A fair die is tossed 240 times, and X denote the number of times that four appeared. |
|
Answer» |
|
| 5937. |
The equation of plane containing the lines barr=(2hatj-3hatk)+lamda(hati+2hatj+3hatk) barr=(2hati+6hatj+3hatk)+lamda(2hati+3hatj+4hatk) |
|
Answer» `(2,6,3)` |
|
| 5938. |
If veca = vec b+ vec c, then is it true that|veca| = |vec b| + |vec c| ? Justify your answer. |
|
Answer» |
|
| 5939. |
Find an anti derivative (or integral) of the following function. (ax+b)^(2) |
|
Answer» |
|
| 5940. |
Evaluate the following integrals intx^(2)cos^(-1)x dx |
|
Answer» |
|
| 5941. |
If sum_(i=1)^(18)(x_(i)-8)=9 and sum_(i=1)^(18)(x_(i)-8)^(2)=45 then find the standard deviation ofx_1 , x_2, ....,x_(18) |
|
Answer» |
|
| 5942. |
If the ecentricity of a hyperbola is srqt3 then the eccentricity of its conjugate hyperbola is |
|
Answer» `SQRT2` |
|
| 5943. |
Let p and be two propositions. Then the contrapositive of the implication p rarr q is |
|
Answer» <P>`~Q RARR ~p` |
|
| 5944. |
The projection of a line segment on the axes are 9, 12 and 8. Then the length of the line segment is |
|
Answer» 15 |
|
| 5945. |
A=[{:(1,-2,3),(-4,2,5):}]andB=[{:(2,3),(4,5),(2,1):}] then find AB and BA . Show that ABneBA. |
|
Answer» |
|
| 5946. |
In the following which is true: |
|
Answer» `(p VV q) vv (-r) -= p vv (q vv r)` |
|
| 5947. |
If x and y are integers, and (x)/(y) is even, which of the following could be true? Indicate all that apply. A. xy is odd B. xy is even C. x+y is odd |
|
Answer» |
|
| 5948. |
Evaluate the following integrals: (i) int_(2)^(3)x^(2)dx (ii) int_(4)^(9)(sqrtx)/((30-x^(3/2))^(2))dx (iii) int_(1)^(2)(xdx)/((x+1)(x+2)) (iv) int_(0)^(pi/4)sin^(3)2tcos2tdt |
|
Answer» |
|
| 5949. |
Thevector (1)/(3) (2hat(i) - 2hat(k)) is |
|
Answer» a unit vectors |
|
| 5950. |
int (x dx)/((x-1)(x-2))" equals : " |
|
Answer» `log|((x-2)^(2))/(x-1)|+C` `RARR "" x=A (x-2) +B(x-1)` x=1 then 1=A (1-2)+0 `rArr` A=-1 x=2 then 2=0 +B(2-1) `rArr` B=2 `:. (x)/((x-1)(x-2))=(1)/((x-1))+(2)/((x-2))` `:. int (x)/((x-1)(x-2)) dx= int ((-1))/(x-1)dx+ int(2)/(x-2)dx` ` =-log |x-1|+2 log |x-2|+c` `=- log |x-1|+log |x-2|^(2)+c` `=log |((x-2)^(2))/(x-1)|+c` `"(":' Log b- log a = log.(b)/(a)")"` |
|