InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 7351. |
Comstruct a_(2xx2) matrix, where a_(ij)=I-2i+3j|. |
|
Answer» |
|
| 7352. |
If sum_(r=1)^(oo) (C^r)/(r!) =1 then C= |
|
Answer» 1 |
|
| 7353. |
The value of int_(-10)^(10) (3^(x))/(3^([x]))dx is equal to |
|
Answer» 20 |
|
| 7354. |
Prove the following : cos(A+B)+sin(A-B) 2sin(45^@+A)cos(45^@+B) |
|
Answer» SOLUTION :R.H.S. = 2sin(`45^@`+A)cos(`45^@`+B) sin(`45^@+A-45^@-B`) sin(`90^@+A+B)sin(A-B) = cos(A+B)sin(A-B) = L.H.S. |
|
| 7355. |
If A = [[2,4],[3,2]] and B = [[1,4],[-3,2]],then 2A + 3B = |
|
Answer» `[[7,20],[-3,10]]` |
|
| 7356. |
Solve the following equation : (i) sin^2x - 5 sin x + 4 = 0(ii) 12x^3+8x=29x^2-4. |
|
Answer» |
|
| 7357. |
A complex number z is said to be unimodular if |z|=1 , Suppose z_1 and z_2 are complex numbers such that (z_1-2z_2)/(2-z_1z_2)is unimodular and z_2 is not unimodular . Then the point z_1 lies on a |
|
Answer» Straight line parallel to x - AXIS |
|
| 7358. |
A machine operates only when all of its three components function. The probabilities of thefailures of the first, second and third components are 0.14,0.10 and 0.05 respectively. What is the probability that the machine will fail. |
|
Answer» |
|
| 7359. |
If A is a square matrix of order 4 then |adj A| is : |
|
Answer» `|A|` |
|
| 7360. |
Prove that {1,4,9,16,25,…...} set are equivalent. |
|
Answer» SOLUTION :`implies` A and D are EQUIVALENT. THUS A,B,C and D are equivalent. |
|
| 7361. |
Integrate the following functions : tan^(-1)((2x)/(1-x^(2))) |
|
Answer» |
|
| 7362. |
If a, b, c ,d be in G.P. , show that (i) (b -c)^(2) + (c - a)^(2) +(d -b)^(2) = (a - d)^(2) (ii) a^(2) + b^(2) + c^(2) , ab + bc + cd , b^(2) + c^(2) + d^(2)are in G.P. |
|
Answer» Solution :(i) Let r be the common ratio of the G.P. than B = ar , ` ar^(2) and d = ar^(3)` L.H.S =`(b-c)^(2) + (c-a)^(2) + (d-b)^(2)` ` = (ar-ar^(2))^(2) + (ar^(2) - a)^(2) + (ar^(3) - ar)^(2)` =` a^(2) r^(2) (1-r)^(2) + a^(2) (r^(2) -1)^(2) + a^(2) r^(2) (r^(2) -1)^(2)` `a^(2) [r^(2) (1 + r^(2) -2R) + (r^(4) + 1 - 2r^(2)) + r^(2) (r^(4) + 1 - 2r^(2))]` =`a^(2) [r^(2) 1 + r^(4) -2r^(3) + r^(4) + 1 - 2r^(2) +r^(6) + r^(2) - 2r^(4)]` `=a^(2)[r^(6) + 2r^(2) - 1]` ` a^(2) (r^(3) -1)^(2)` `= [a(r^(3) -1)]^(2)` = `(ar^(3) -a)^(2)` ` (d -a)^(2)` ` = (a -d)^(2)` Let r be the common ratio of the G.P. than`b = ar , c ar^(2) and d = ar^(3)` Now, ` a^(2) + b^(2) + c^(2) = a^(2) +a^(2) r^(2) + a^(2) r^(4) = a^(2) (1 + r^(2) + r^(4))` `ab + bc + CD = a^(2) r + a^(2) r^(3) + a^(2) t^(5) = a^(2)r(1 + t^(2) + r^(4))` ` b^(2) + c^(2)+d^(2) =a^(2)r^(2) + a^(2) r^(4) + a^(2) t^(6) = a^(2)r^(2)(1 + t^(2) + r^(4))` Clearly , `(ab + bc + cd)/(a^(2)+ b^(2) + c^(2))=(b^(2) + c^(2)+d^(2))/(ab + bc + cd)` Hence , ` a^(2) + b^(2) + c^(2) , ab + bc + cd , b^(2) + c^(2) + d^(2)` are in G.P. |
|
| 7363. |
If f(x)=sqrt((3x-6)/(x+2))+root(4)((x^(4)-5x^3+6x^(2))(1-x^(2))), find complex values of x , for which f(x) isreal |
|
Answer» |
|
| 7364. |
If (-4,5) is one vertex and 7x-y+8 = 0 is one diagonal of a square, then the equation of the second diagonal is |
|
Answer» X + 3Y = 21 |
|
| 7365. |
Find the area of atriangle having the points A(1,1,1), B (1,2,3) and C(2,3,1) as its vertices. |
|
Answer» |
|
| 7366. |
Evalute the following integrals int (x + 2) sqrt(x + 1) dx |
|
Answer» `(2)/(5)(x-1)^(3//2)(3x+8)+C` |
|
| 7367. |
If x ge 0, y ge 0, 2x+3y le 10 and x+2y ge 10 then the minimum value of f=2x+3y is |
|
Answer» `10//3` |
|
| 7368. |
Consider the traingle having vertices O(0,0),A(2,0), and B(1,sqrt3). Also b le"min" {a_1,a_2,a_3....a_n} meansb le a_1 when a_1 is least, b le a_2 when a_2 is least, and so on. Form this, we can say b le a_1,b le a_2,.....b le a_n. Let R be the region consisting of all those points P inside DeltaOAB which satisfy d(P,OA)le "min"[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line. then the area of the region R is |
|
Answer» `SQRT(3)`sq,units  `d(P,OA)le min[d(P,OB),d(P,AB)]` or `d(P,OA)le(P,OB)` and `d(P,OA0)le d(P,AB)` When `d(P,OA)P` is equidistant from OA and OB, or P lies on the BISECTOR of lines OA and OB. Hence, when `d(P,OA)le d(P,OB)`, point P is nearer to OA than to OB or lies below the angle bisector of `angleAOB`. Similarly, when `d(P,OA)led(P,AB)P` is nearer to OA than to AB, or P lies below the bisector of `angle OAB and AB`. THEREFORE, the required area is equal to the area of `DeltaOIA`. Now, `tanangleBOA=(sqrt3)/(1)=sqrt3` or `angle BOA=60^@` Hence, the TRIANGLE is equilateral. then I coincides. with the centroid which is `(1,1//sqrt3)`. Therefore,the area of `Delta OIA` is `(1)/(2) OAxxIM=(1)/(2)xx2xx(1)/(sqrt3)=(1)/(sqrt3)`sq.units |
|
| 7369. |
Consider the traingle having vertices O(0,0),A(2,0), and B(1,sqrt3). "Also" b le"min" {a_1,a_2,a_3....a_n} meansb le a_1 when a_1 is least, b le a_2 when a_2 is least, and so on. Form this, we can say b le a_1,b le a_2,.....b le a_n. Let R be the region consisting of all the those points P inside DeltaOAB which satisfy.OPle"min"[BP,AP]. Then the area of the region R is |
|
Answer» `SQRT(3)`sq,units 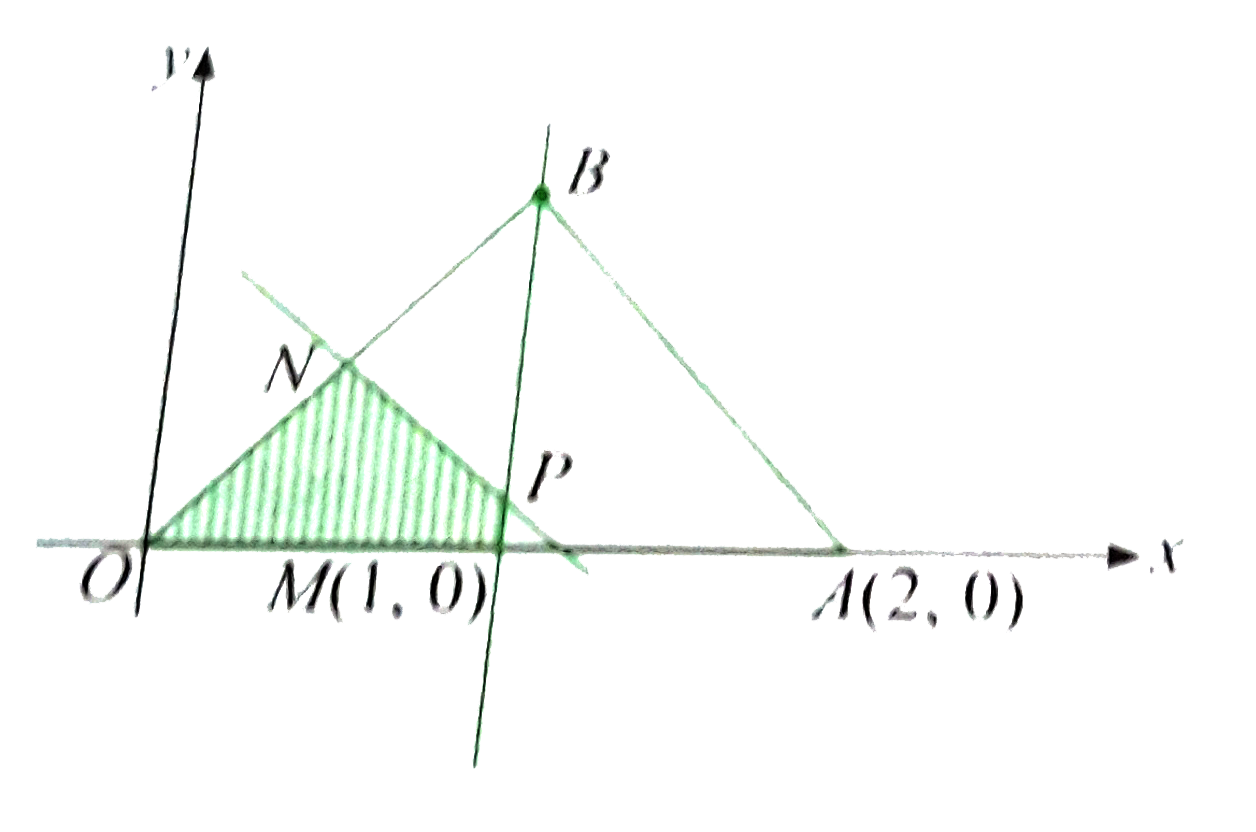 `OP le "min"[BP,AP]` `OP le AP(whenAPlt BP)` LET `OP=BP`. The P lies on the perpendicular bisector of OB, For `OP=AP,P` lies on the perpendiuclar bisector of OA. Then, for the required condition, P lies in the REGION as shown in the diagram. the AREA of region `OMPN` is `(1)/(2)xx|{:(0,,0,,),(1,,0,,),(1,,1//sqrt3,,),(1/2,,sqrt(3)//2,,),(0,,0,,):}|=(1)/(2)[(1)/(sqrt3)+(sqrt3)/(2)-(1)/(2sqrt3)]` `=(1)/(2)[sqrt(3)/(2)+(1)/(sqrt3)]=(1)/(sqrt3)` |
|
| 7370. |
If f(x)=Ax^(2) +Bx satisfies the conditions f^(1)(1)=8 and int_(0)^(1) f(x)dx=8/3, then |
|
Answer» `A=1, B = -4` |
|
| 7371. |
Let PQ be a focal chord of the parabola y^(2) = 4ax. The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a,a gt 0. If chord PQ subtends an angle theta at the vertex of y^(2) = 4ax, then tan theta is equal to |
|
Answer» `(2)/(3) SQRT(7)` 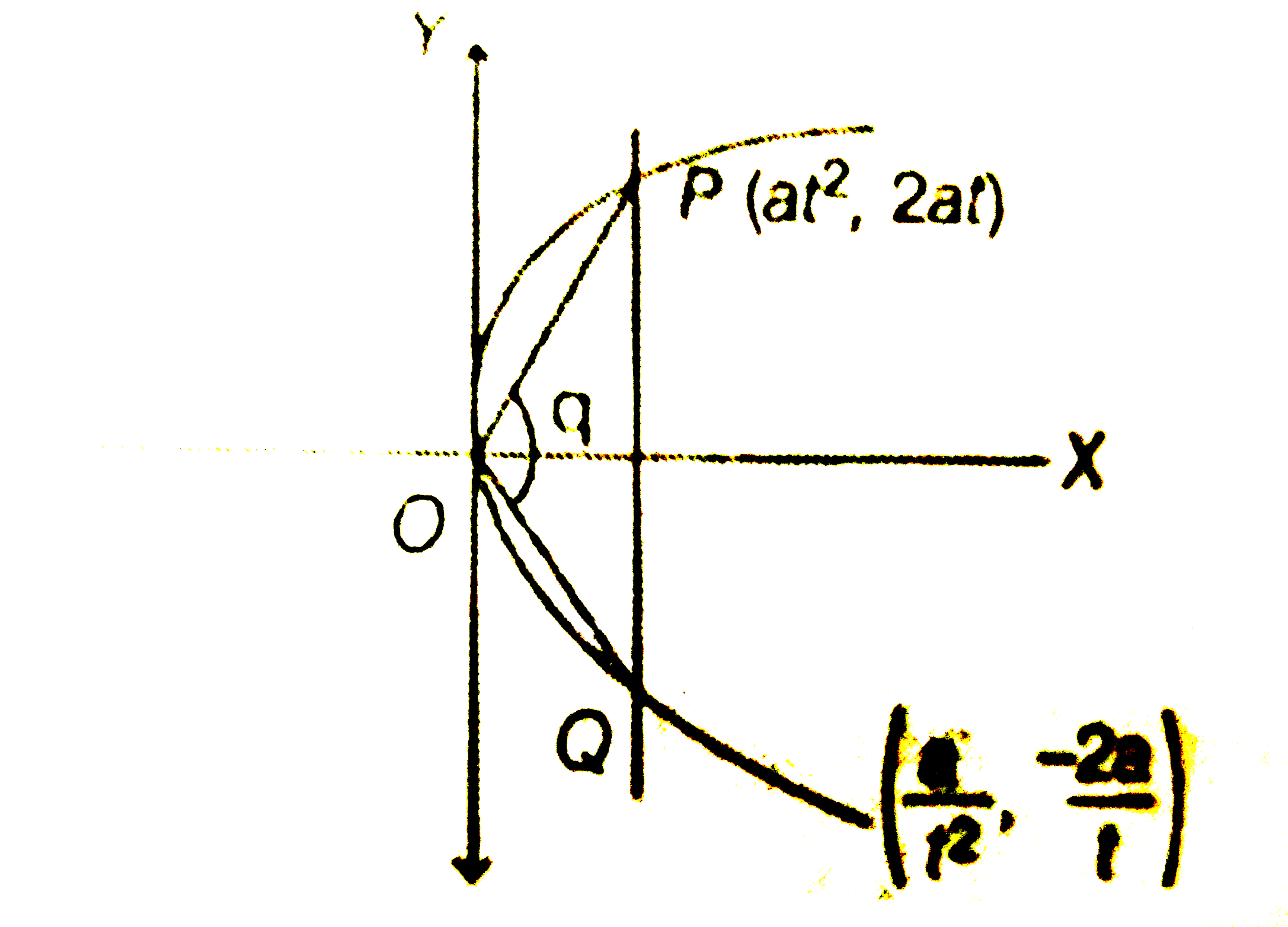 `m_(OQ) = (-2a//t)/(a//t^(2)) = - 2T` `:. TAN theta = ((2)/(t) + 2t)/(1 - (2)/(t).2t) = (2(t - (1)/(t)))/(1 - 4) = (-2 sqrt(5))/(3)` Where `t + (1)/() = sqrt(5)` |
|
| 7372. |
Let be a function from a st X to a set Y. Consider the following statements: P : For each x in X, there exists unique y in Y such that f(x)=y Q : For each y in Y, there exists x in X such that f(x) = y. R: there exist x underset 1, x underset 2 in X such that x underset 1 != xunderset 2 and f(x underset 1) = f(x underset 2). The negation of the statement "f is one-to-one and onto" is |
|
Answer» <P>P or not R |
|
| 7373. |
Find the possible set of values of x for which expansion of (3-2x)^(1//2) is valid in ascending powers of x. |
|
Answer» |
|
| 7374. |
If f(x)=2x^(2)-3x+5 then find the approximate value of f(1.05). |
|
Answer» |
|
| 7375. |
From the differential equation representing the family of ellipses having focion x-axis and centre at the origin. |
|
Answer» |
|
| 7376. |
(d)/(dx) [x+(x ^(3))/(3 ) + (x ^(5))/(5) +...]= |
|
Answer» `(d)/(DX) [X+(x ^(3))/(3 ) + (x ^(5))/(5) +...]=` |
|
| 7377. |
Solve z^(4)-16i=0 where z to c complex no. |
|
Answer» |
|
| 7378. |
On N, define a relation R as follows: a, b in N, aRb if a|b Then which of the following is not true? |
|
Answer» R is reflexive |
|
| 7379. |
Volume of a tetrahedron is k (area of one face) (length of perpendicular from the opposite vertex upon it), where k is : |
|
Answer» `(1)/(4)` |
|
| 7380. |
Radius of the circle centred at (3,-2) , or maximum area contained in the circle x ^(2) + y ^(2) - 4x + y=0 is |
|
Answer» `(1//2) (SQRT17- SQRT13) ` |
|
| 7381. |
Find the equation of circle passing through (1, 1) belonging to the system of co-axial circles that are tangent at (2, 2) to the locus of the point of intersection of mutually perpendicular tangent to the circle x^(2) + y^(2) = 4. |
|
Answer» |
|
| 7382. |
If the eccentricity of the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2))=1 is (5)/(4) and 2x+3y-6=0 is a focal chord of the hyperbola, then the length of transverse axis is equal to _________ |
|
Answer» `(5)/(24)` |
|
| 7383. |
The rate of change of area of a circle with respect to its radius at r=2cm is of |
| Answer» Answer :D | |
| 7384. |
By using the properties of definite integrals evaluate the integrals in exercise. overset(8)underset(2)int |x-5|dx |
|
Answer» |
|
| 7385. |
An examination consists of 10 multiple choice questions, where each question has 4 options, only one of which is correct. In every question, a candidate earns 3 marks for choosing the correct opion, and -1 for choosing a wrong option. Assume that a candidate answers all questions by choosing exactly one option for each. Then find the number of distinct combinations of anwers which can earn the candidate a score from the set {15, 16,17,18, 19, 20}. |
|
Answer» `therefore` His score is `3x+(10-x)(-1)=4x-10` Now score of the candidate is from the set {15,16,17,18,19,20}. Only 4x-10=18 is possible . `therefore x=7` So, his 7 answer are CORRECT and 3 answers are wrong. Number of ways of selection of 7 questions from `10= .^(10)C_(7)= .^(10)C_(3)` `=(10xx9xx8)/(6)=120` |
|
| 7386. |
Find the values of the following integrals (i) int_(-2 pi)^(2pi) cos^(6)x dx |
|
Answer» 0 |
|
| 7387. |
If a = 7 , b= 3, c=5 then find A. |
|
Answer» SOLUTION :If a = 7 , B= 3, c=5 then cosA = `(b^2 + c^2 + a^2)/(2bc) = (9 + 25 - 49)/(2 xx 3 xx 5) = (-15)/(2xx3xx5) = -1/2` `THEREFORE` cosA = -1/2 or A = `120^@` |
|
| 7388. |
if A[{:(1,3,-1),(2,2,-1),(3,0,-1):}]and B=[{:(-2,3,-1),(-1,2,-1),(-6,9,-4):}],thenshowthat AB=BA. |
|
Answer» |
|
| 7389. |
If a line makes angles 90^(@),135^(@)and45^(@) with the X, Y and Z-axis respectively, find its direction cosines. |
|
Answer» |
|
| 7392. |
int(x^(3))/(sqrt(1+x^(2)))dx=a(1+x^(2))^((3)/(2))+b* sqrt(1+x^(2))+C |
|
Answer» `a=(1)/(3) and b=1` |
|
| 7393. |
P is a point inside the equilateral traingle ABC such that PA=1cm, PB=sqrt(2)cm and PC=sqrt(3).Then the side of the traingle("in cm") equal. |
|
Answer» `SQRT(6-2sqrt(3))` `cos theta=(a^(2)+1-2)/(2A)=(a^(2)-1)/(2a)` In `DeltaPAC` `cos (60-theta)=(1+a^(2)-3)/(2a)=(a^(2)-2)/(2a)` `therefore cos theta +cos (60-theta)=(2a^(2)-3)/(2a)implies cos(30-theta)=(2a^(2)-3)/(2sqrt(3a))` `"ALSO", ""costheta-cos(60-theta)=(1)/(2a)impliessin(30-theta)=(1)/(2a)` `implies((2a^(2)-3)/(2sqrt(3a)))^(2)+((1)/(2a))^(2)=1` `implies4a^(4)-24a^(2)+12=0` `impliesa^(2)=3+sqrt(6)` or `a=sqrt(3+sqrt(6))` 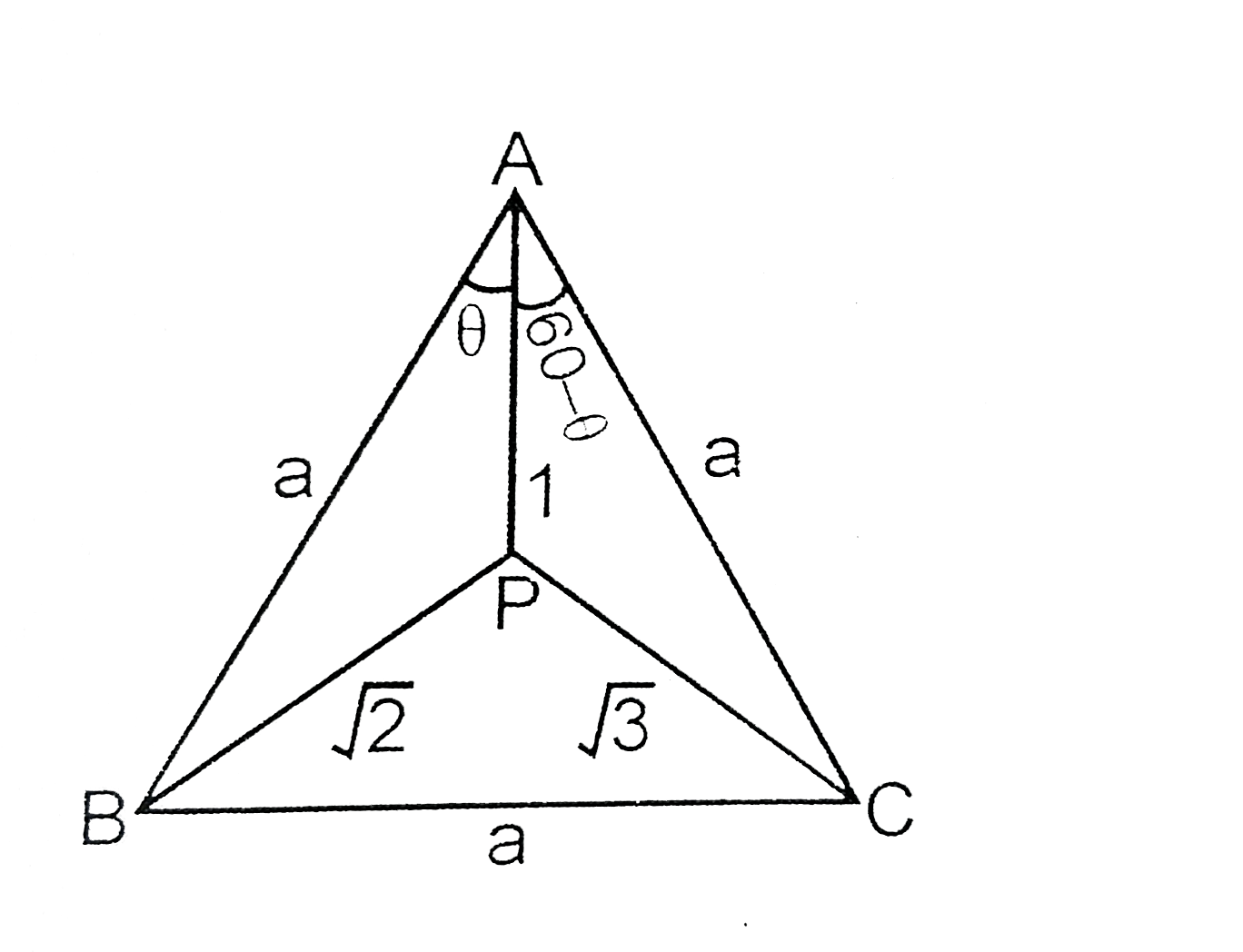
|
|
| 7394. |
The value of lim_(x to oo)(e^(1//x)-e^(-1//x))/(e^(1//x)+e^(-1//x)) tan (1/x) is |
| Answer» ANSWER :B | |
| 7395. |
Let Z be a complex number satisfying the relation Z^(3)+(4(barZ)^(2))/(|Z|)=0. If the least possible argument of Z is -kpi, then k is equal to (here, argZ in (-pi, pi]) |
|
Answer» |
|
| 7396. |
Find the work done is calorie when 65.5g Zn reacts with excess H_(2)SO_(4) (aq) to form ZnSO_(4) & H_(2) in a closed rigid vessel at 300 K. |
|
Answer» -600 |
|
| 7397. |
The numbers 1,2,3,..n are arranged in a random order. The probability that the digits 1,2,3,….k(k lt n) appear as neighbours is |
|
Answer» `((N - K) !)/(n !)` |
|
| 7398. |
If log x = (-1)/3 log y = 2/5 " and " P =log ( sin ( arc cos sqrt(1 - x^(2)))) Q = log (cos ( arc tan sqrt(1-x^(2)y^(2))/(xy))), then |
|
Answer» `P = (-1)/9` |
|
| 7399. |
int (5x^3+18x^2-10x-6)/(x(x+3)(5x-2)) dx |
|
Answer» |
|
| 7400. |
A plane cutting the axes in P, Q, R passes through (alpha-beta, beta-gamma, gamma-alpha). If O is the origin, then locus of centre of sphere OPQR is |
|
Answer» `alphax+betay+gammaz=4` |
|