Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

9851.

The vectors a=hati+hatj+mhatk, b=hati+hatj+(m+1)hatk and c=hati-hatj+mhatk are coplanar, it m is equal to

Answer»

1
4
3
no value of m for which VECTORS are coplanar

Solution :Given vectors are coplanar, if
`|(1,1,m),(1,1,m+1),(1,-1,m)|=0implies|(0,0,-1),(1,1,m+1),(1,-1,m)|=0
[R_(1)rarrR_(1)-R_(2)]`
`implies -1(-1-1)=0`
`implies 2 NE 0`
`therefore` No value of m for which vectors are coplanar.
Discussion
9852.

int(1)/(1-cosx)dx

Answer»


ANSWER :`-cotx-cosecx+c`
Discussion
9853.

The vertex of a parabola if es on with one of the vertices of the ellipse (x ^(2))/(a ^(2)) + y ^(2))/(b ^(2))=1 and its axis is along the major axis of the ellipse. For the area or the region bounded by the parabola and its common chord (not passing through the vertex) with the ellipse to be maximum, prove that the latus rectum of the ellipse is four times that of the parabola.

Answer»


ANSWER :`=> (2B^(2))/(a) = 4L.`
Discussion
9854.

Differentiate ax^2+btanx+lnx^3

Answer»

SOLUTION :`y=ax^2+btanx+lnx^3`
`dy/dx=2ax+bsec^2x+3/x`
Discussion
9855.

If the m inor axis of an ellipse form s an equilateral triangle with one vertex of the ellipse then e =

Answer»


ANSWER :`SQRT(2/3)`
Discussion
9856.

Find (dy)/(dx) if 2x+3y=siny

Answer»

SOLUTION :Differentiatingboth sides w.r.t.x, we have `2+3(dy)/(DX)=COSY(dy)/(dx)(cosy-3)(dy)/(dx)=2(dy)/(dx)=2/(cosy-3)`
Discussion
9857.

The quadratic expression (2x+1)^(2)-px +q ne 0 for any real x if

Answer»

`p^(2) -16P -8q LT 0`
`p^(2) -8p +16qlt 0`
`p^(2)-8p-16q lt 0`
`p^(2) -16p +8q lt 0`

ANSWER :C
Discussion
9858.

If |z| = 1 and arg [z^(2) + barz] = x arg z then x

Answer»

`(1)/(2)`
2
`(3)/(2)`
1

Answer :A
Discussion
9859.

int(log(x+sqrt(1+x^(2))))/(sqrt(1+x^(2)))dx=....+c

Answer»

`(1)/(2)[LOG(x+sqrt(1+x^(2)))]^(2)`
`log[x+sqrt(1+x^(2))]^(2)`
`log(x+sqrt(1+x^(2)))`
NONE of these

Answer :A
Discussion
9860.

Let S be the set of all complex numbers z satisfying | -2+i|ge sqrt(5).if the complex number z_(0) is such that (1)/(|z_0-1|) is the maximum of the set {(1)/(|z-1|): ζinS}, then the principal argument of (4-z_0-overline(z)_0)/(z-overline(z)_0+2i) is

Answer»

`(pi)/(4)`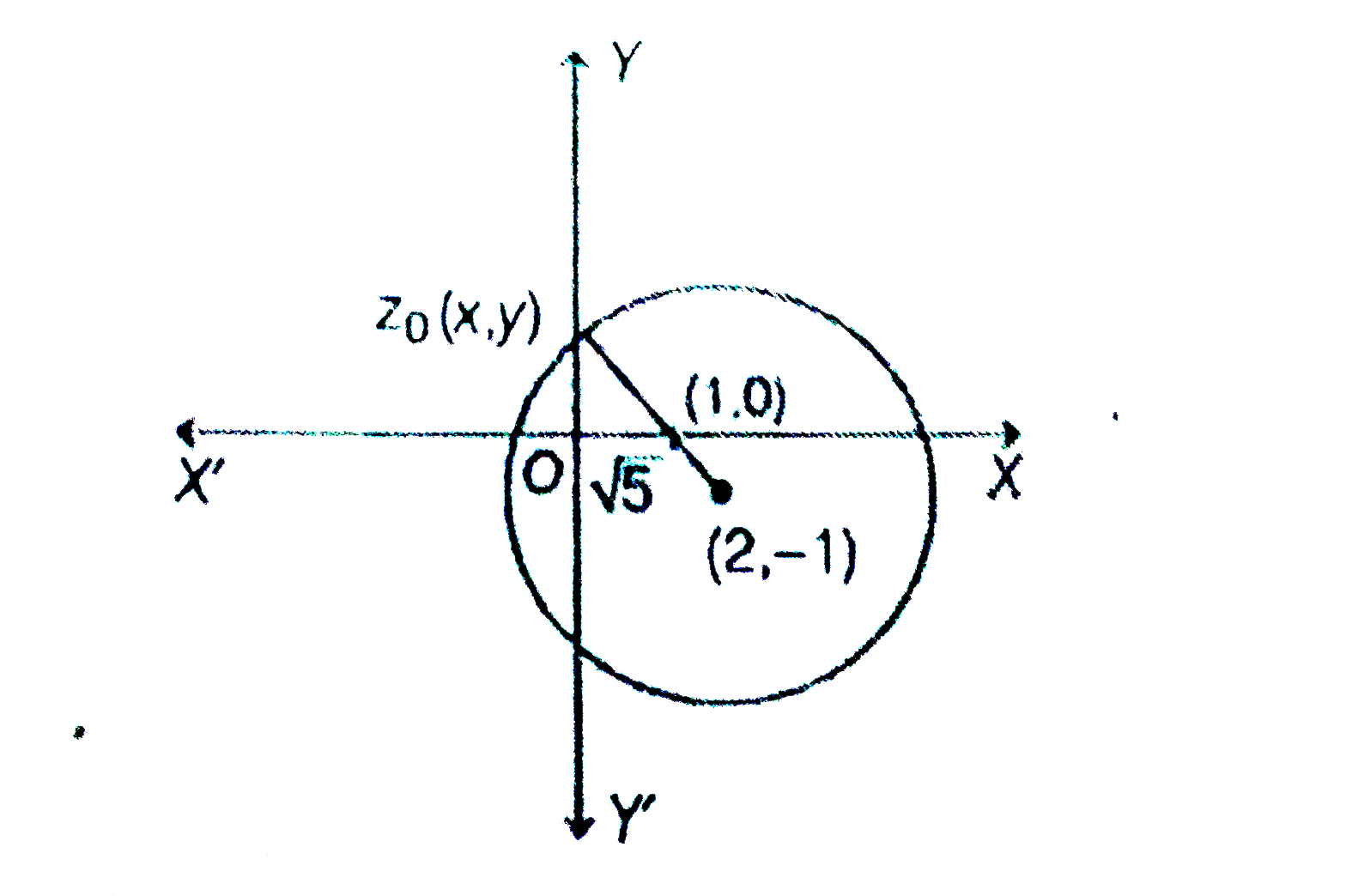
`(3pi)/(4)`
`-(pi)/(2)`
`(pi)/(2)`

Solution :The complex NUMBER ` z` satisfying `| z-2 +i|ge sqrt(5)`, which represents the region outside the circle (including the circumference )having centre `(2,-1)` and radius `sqrt(5)` units.

Now, for ` z_(0) in S(1)/(| z_(0)-1|)` is maximum.
When `| z_0-1|` is minimum. And for this it is required that `z_0` is collinear with the points `(2,-1)` and `(1,0)` and LIES on the circumference of the circle `|ᶼ-2+i|=sqrt(5)`.
So let `z_0=X+iy`, and the figure `0lt x lt 1 and y gt 0`.
So, `(4-z_(0)-overline(z)_(0))/(z_0-overline(z)_(0)+2i)=(4-x-iy-x+iy)/(x+iy-x+iy+2i)=(2(2-x))/(2i(y+1))=-i((2-x)/(y+1))`
`because (2-x)/(y+1)` isa positive real number, so
`(4-z_0-overline(z)_0)/(z_0-overline(z)_0+2i)` is PURELY negative imaginary number.
`rArr arg ((4-z_0-overset(-)z_(0))/(z_0-overset(-)z_(0)+2i))=-(pi)/(2)` .
Discussion
9861.

If (a, a^(2)) falls inside the angle made by the lines y=(x)/(2), x gt 0 and y = 3x, x gt 0, then a belongs to

Answer»

`(0, (1)/(2))`
`(3, infty)`
`((1)/(2), 3)`
`(-3, -(1)/(2))`

ANSWER :C
Discussion
9862.

The value of int_(-pi)^(pi)(cos^(2)x)/(1+a^(x))dx,agt0 is

Answer»

`2 PI`
`pi/a`
`pi/2`
`a pi`

ANSWER :C
Discussion
9863.

Integrate the function in Exercise. x sin^(-1)x

Answer»


Answer :`(1)/(4)(2X^(2)-1)SIN^(-1)x+(1)/(4)x SQRT(1-x^(2))+C`
Discussion
9864.

Check the validity of the statements given below by the method given against it. (i) p: The sum of an irrational number and a rational number is irrational (by contradiction method). (ii) q: If n is a real number with n gt 3, then n^(2)gt9 (by contradiction method).

Answer»


ANSWER :then `N^(2)lt9` " is TRUE.
Discussion
9865.

Find the locus of the centriod of an equilateral triangle inscribed in the ellipse x^(2)/a^(2)+y^(2)/b^(2)=1.

Answer»
Discussion
9866.

Let s_(n) denote the sum of first n terms of an A.P. and S_(2n) = 3S_(n). If S_(3n) = kS_(n) then the value of k is equal to

Answer»

4
5
6
7

Answer :C
Discussion
9867.

Let the incircle of a Delta ABC touches sides BC, CA and AB at D,E and F, respectively. Let area of Delta ABC be Delta and thatof DEF be Delta'. If a, b and c are side of Dela ABC, then the value of abc(a+b+c)(Delta')/(Delta^(3)) is

Answer»

1
2
3
4

Solution :
Clearly points C, D, I and E are concyclic
`therefore angle EID = pi - C`
`therefore` In `Delta DEF, angle DFE =(pi-C)/(2)`
Similarly `angle EDF =(pi-A)/(2)` and `angle FED = (pi-B)/(2)`
`Delta' =2R^(2)SIN((pi-A)/(2))sin((pi-B)/(2))sin((pi-C)/(2))`
`=2r^(2)cos((A)/(2))cos((B)/(2))cos((C )/(2))`
`therefore abc (a+b+c)(Delta')/(Delta^(3))`
`=(abc(a+b+c))/(Delta^(3))2r^(2)cos.(A)/(2)cos.(B)/(2)cos.(C )/(2)`
`=(abc(2s))/(Delta^(3))2r^(2)cos.(A)/(2)cos.(B)/(2)cos.(C )/(2)`
`=(abc(2s))/(Delta^(3))2r^(2)sqrt((s(s-a))/(bc))sqrt((s(s-b))/(ab))sqrt((s(s-c))/(ac))`
`=(4abcs)/(Delta^(3))r^(2)(s)/(abc)sqrt(s(s-a)(s-b)(s-c))`
`=(4S^(2))/(Delta^(2))r^(2)`
= 4.
Discussion
9868.

The number of ways to choose 7 distinct natural numbers from the first 100 naturalnumbers such that any two chosen numbers differ atleast by 7 can be expressed as ""^(n)C_(7). Find the number of divisors of n.

Answer»


ANSWER :7
Discussion
9869.

Which of the following is CORRECT combination ?

Answer»

`(II) (i) (S) `
`(I) (III) (Q) `
`(I) (iii) (P) `
`(IV) (ii) (R )`

SOLUTION :N/A
Discussion
9870.

Write down the sequence whose n ^(th) term is ( (-2) ^(n))/( (-1) ^(n) +2)

Answer»


ANSWER :`16/3`
Discussion
9871.

Let vec(a),vec(b) and vec(c) be three independent vectors In the vector vec(a)+2vec(b)+lamdavec(c)=lamdavec(a)+muvec(b)+vec(c), then

Answer»

`lamda=mu`
`lamda=2mu`
`lamda=1,mu=2`
`lamda=mu^(2),mu=lamda^(2)`

ANSWER :C
Discussion
9872.

Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.

Answer»

SOLUTION :`A=pir^2(DA)/(DR)=2pir,(dA)/(dr)|_(r=3)=6picm^2//cm`
Discussion
9873.

{:("List-I","List-II"),(P.y = x^(2) + 2 y = - x. x = 0 "and" x = 1, 1. 4//3),(Q. y = x^(2). Y = 2//(1 + x^(2)),2.2sqrt(2)),(R.y = sin x y cos x "one of the regions",3. pi - (2)/(3)),(S.x = - 2y^(2) X = 1 - 3y^(2), 4. 17//6):}

Answer»

2,4,1,3
1,2,3,4
3,4,1,2
4,3,2,1

Answer :D
Discussion
9874.

If A=[{:(2,3),(1,-4):}] and B=[{:(1,-2),(-1,3):}] then verify that (AB)^(-1)=B^(-1)A^(-1)

Answer»


ANSWER :`(AB)^(-1)=B^(-1)A^(-1)`
Discussion
9875.

If possible using elementary row transformations, find the inverse of the following matrices. (i) [{:(2,-1,3),(-5,3,1),(-3,2,3):}]

Answer»

SOLUTION :For getting the inverse of the given matrix A by row elementary operations we may write the given matrix as
A=IA
(i) `because [{:(2,-1,3),(-5,3,1),(-3,2,0):}]=[{:(1,0,0),(0,1,0),(0,0,1):}]A`
`RARR [{:(2,-1,3),(-3, 2,4),(-3,2,3):}]=[{:(1,0,0),(1,1,0),(0,0,1):}]A [because R_(2)rArrR_(2)+R_(1)]`
`rArr[{:(2,-1,3):}]=[{:(1,0,0),(1,1,0),(0, 0,1):}]A[becauseR_(3)rArrR_(3)-R_(2)]`
`rArr [{:(-1,1,7),(-3,2,4),(0,0,-1):}]=[{:(2,1,0),(-5,-2,0),(-1,-1,1):}]A[because R_(2)rArrR_(2)-3R_(1)]`
`rArr[{:(-1,0,-10),(0,-1,-17),(0,0,1):}]=[{:(-3,-1,0),(-5,-2,0),(1,1,-1):}]A[because R_(1)rArrR_(1)+R_(2)"and" R_(3)rArr-1.R_(3)]`
`rArr[{:(1,0,0),(0,1,0),(0,0 ,1):}]=[{:(-7,-9,10),(1,1, -1):}]A[because R_(1)rArr-1R_(1) "and" R_(2)rArr-1R_(2)]`
So, the inverse of A is `=[{:(-7,-9,10),(-12,-15,17),(1,1,-1):}]`
(ii) `THEREFORE [{:(2,3,-3),(-1,-2,2),(1,1,-1):}]=[{:(1,0,0),(0,1,0),(0,0,1):}]A`
`rArr [{:(0,1,-1), (0,-1,1),(1,1,-1):}]=[{:(1,0,-2),(0,1,1),(0,0,1):}]A [because R_(2)rArrR_(2)+R_(3) "and" R_(1)rArrR_(1)-2R_(3)]`
`rArr[{:(0,1,-1),(0,0,0),(1,1,1):}]=[{,(1,0,-2),(2,1,-2),(0,0,1):}] [because R_(2)rArrR_(2)+R_(1)]`
Since, second row of the matrix A on LHS is containing all zeroes, so we can say that inverse of matrix A does not exist.
(iii) `therefore [{:(2,0,-1),(5,1,0),(0,1,3):}]=[{:(1,0,0),(0,1,0),(0,0, 1):}]A`
`rArr[{:(2,0,-1),(3,1,1),(0,1,3):}]=[{:(1,0,0),(-1,1,0),(0,0,1):}]A[because R_(2)rArrR_(2)-R_(1)]`
`rArr [{:(2,0,-1),(1,1,2),(2,1,2):}]=[{:(1,0,0),((-5)/(2),1,0),(2, 0,1):}]A[because R_(3)rArrR_(3)+R_(1)"and" R_(2)rArrR_(2)-(1)/(2)R_(1)]`
`rArr[{:(2,0,(-1),(0,1,(5)/(2)),(0,1,3):}]=[{:(1,0,0),((-5)/(2),1,0),(0,0,1):}][because R_(3)rArrR_(3)-2R_(1)]`
`rArr [{:(1,0,(-1)/(2)),(0,1,(5)/(2)),(0,0,1):}]=[{:(because R_(1)rArr(1)/(2)R_(1) "and" R_(3)rArr2R_(3)]`
`rArr [{:(1,0,0),(0,1,0),(0,0,1):}]=[{:(3,-1,1),(-15,6,-5),(5,-2,2):}]A[{:(because R_(1)rArrR_(1)R_(1)+(1)/(2)R_(3) "and" R_(2)rArrR_(2)-(5)/(2)R_(3)]`
HENCE, `[{:(3,-1,1),(-15,6,-5),(5,-2,2):}]` is the inverse of given matrix A.
Discussion
9876.

The scatterplot above shows the daily profit made by a school store from selling sweatshirts and the average daily temperature for several days in the year 2004. The line of best fit is also shown and has equation y=-4.1x+446. Which of the following best explains hoow the number -4.1 in the equation relates to the scatterplot?

Answer»

For every `1^(@)` increase in average daily temperature, the school STORE's profit fell by approximately $4.10/
For every `1^(@)` increase in average daily temperature, the school store's profit fell by approximately $4.10/
For every `4.1^(@)` increase in average daily temperature, the school store's profit fell by approximately $4.10/
For every `4.1^(@)` increase in average daily temperature, the school store's profit fell by approximately $4.10/

Answer :A
Discussion
9877.

If a matrix has 28 elements , what are the possible orders it can have ? What if it has 13 elements ?

Answer»


ANSWER :`=13xx1and1xx13`.
Discussion
9878.

int_(- pi/4)^(pi/4) cos^(-4) x dx=

Answer»

` - 8/3`
`8/3`
`- 3/8`
`3/8`

ANSWER :B
Discussion
9879.

Expression of x+y + z = 1 in the form of x cos alpha + y cos beta + z cos gamma = p is ..........

Answer»

` x + y + z=1`
`(x)/(2sqrt(3)) + (y)/(2sqrt(3)) + (x)/(2sqrt(3))= (1)/(SQRT(3))`
`(x)/(sqrt(3)) + (y)/(sqrt(3)) + (z)/(sqrt(3)) = 1`
`(x)/(sqrt(3)) + (y)/(sqrt(3)) + (z)/(sqrt(3)) = (1)/(sqrt(3))`

ANSWER :D
Discussion
9880.

If 3x - 4y + k = 0is a tangent to x^(2) - 4y^(2) = 5find thevalue of k.

Answer»


ANSWER :`K = PM 5`
Discussion
9881.

intsqrt(1-sin2x)dx

Answer»

SOLUTION :`I=intsqrt(1-sin2x)DX`
=`intsqrt((cosx-sinx)^2)dx`
=`INT(cosx-sinx)dx`
=sinx+cosx+c
Discussion
9882.

Prove that the tangent at (3,-2) of the circlex^(2) +y^(2) = 13touches the circle x^(2) + y^(2) + 2x - 10 y- 26 = 0 and find its point of contact.

Answer»


ANSWER :(5,1)
Discussion
9883.

If a spherical rain drop evaporates at a rate proportional to its surface area. Form a differential equation indicating the rate of change of the radius of the rain drop.

Answer»


ANSWER :INDEPENDENT
Discussion
9884.

Using properties of determinant, find the value of x: |{:(x+a, a^(2), a^(3)), (x+b, b^(2), b^(3)), (x+c, c^(2), c^(3)):}|=0

Answer»


ANSWER :`(-ABC)/(ab+bc+ca)`
Discussion
9885.

Find both the maximum value and the minimum value of 3x^(4) – 8x^(3) + 12x^(2) – 48x + 25 on the interval [0, 3].

Answer»


Answer :MINIMA at X = 2, minimum value = – 39, Maxima at x = 0, maximum value = 25.
Discussion
9886.

Thenumber of waysthatall thelettersof thewordSWORDcan bearrangedsuchthatnoletteris in itsoriginalposition is

Answer»

44
32
28
20

Answer :A
Discussion
9887.

If f(x) =tan , x in [0.(pi)/(5)] then show that (pi)/(5) lt ((pi)/(5)) lt (2pi)/(5)

Answer»
Discussion
9888.

Match the following {:("I.","The approximate value of"sin (30^@ 1^1),"a",1.00058),("II".,"The approximate value of" cos(61^@),b,1.0349),("III.","The approximate value of"tan (46^@),c,0.4849),("IV.","The approximate value of" (45^@ 1^'),d,0.50025):}

Answer»

C,B,d,a
d,c,b,a
c,d,a,b
c,b,d,a

Answer :B
Discussion
9889.

Ifvec a =hati +3hatj , vecb = 2hati -hatj - hatk and vec c =mhati +7 hatj +3hatkare coplanar then find the value of m.

Answer»


ANSWER :` m=0 `
Discussion
9890.

int(x^(2))/((xsinx+cosx)^(2))dx

Answer»


ANSWER :`TANX-(xsecx)/(xsinx+cosx)+C`
Discussion
9891.

No. of solution ge 7 for

Answer»

SIN x = `x //10`
Sin `x = x^(2) + x + 1`
`2^("cos x") = |sin x| , x in [0 , 2pi]`
Not

Answer :A
Discussion
9892.

For A=[a_(ij)]_(nxxn)'a_(ij)=0,i nej then is a .... matrix . (a_(ii)nea_(ij)),(ngt1)

Answer»

RAW matrix
column matrix
Diagonal matrix
Scalar matrix

Answer :C
Discussion
9893.

Findint (2x^(2)-5x+1)/( x^(2)(x^(2)-1))dx.

Answer»


ANSWER :`(1)/(x)+LOG|(x^(3))/((x^(2)-1)(x+1)^(3))|+C`
Discussion
9894.

If |veca*vecb|=sqrt3|vecaxxvecb|,then angle between veca and vecb is :

Answer»

`FRAC{pi}{2}`
`frac{pi}{4}`
`frac{pi}{3}`
`frac{pi}{6}`

ANSWER :D
Discussion
9895.

Juliet a selling photographs as part of a project for her entrepreneurship class. She sells the first 20 photographs for $10 each. Because the first 20 photographs sold so quickly, she raised the price of the photographs to $15 each for the rest of the project. After her expenses, Juliet earns a profit of 80% of the revenues from her sales. What is the least number of photographs she must sell for the rest of the project of earn a profitof at least $400?

Answer»

18
20
24
32

Answer :B
Discussion
9896.

Let f(X) be real valued continous funcion on R defined as f(X) =x^(2)e^(-|x|) The values of k for which the equation x^(2)e^(-|x|)=k has four real roots are

Answer»

`0ltklte`
`0ltklt(8)/(e^(2))`
`0ltklt(4)/(e^(2))`
none of these

Solution :We have `F(X)=x^(2)e^(-|x|={{:(x^(2)e^(-x),xge0),(x^(2)e^(x),xlt0):}`
`therefore f(X) ={{:(e^(-x)(2x-x^(2)),xge0),(e^(x)(x^(2)+2x),xlt0):}`
F(x) increasing in `(-oo,-2)CUP(0,2)` and f(x) DECREASING `(-2,0)cup(2,o)` THUS
`f(x)={{:(e^(-x)(x^(2)-4x+2),xge0),(e^(x)(x^(2)+4x+2y),xlt0):}`

f(x)=0 has FOUR roots hence there are four points of inflection
Discussion
9897.

A perfectely rough plane is inclined at an angle alpha to the horizontal. Then the laeast eccentricit of an ellipse which can rest on the plane is

Answer»

`2sqrt(sin ALPHA)`
`SQRT((2 sin alpha)/(1+sin alpha))`
`sqrt((2 sin alpha)/(1+cos alpha))`

ANSWER :B
Discussion
9898.

int_2^3(dx)/sqrt(x^2-2)

Answer»

SOLUTION :`int_2^3(DX)/SQRT(x^2-2)`
`[In(x+sqrt(n^2-2)]_2^3`
`In(3+sqrt7)=In(2+sqrt2)`
`In((3+sqrt7)/(3+sqrt2))`
Discussion
9899.

If the area of the triangle on the complex plane formed by the point z, iz and z +iz is 50 square units , then |z| is

Answer»

5
10
15
20

Answer :B
Discussion
9900.

If p and q are two statement then a statement which is always true is

Answer»

`PVVQ`
`p^^q`
`pvv~q`
`qvv~q`

ANSWER :D
Discussion