InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10301. |
Evalute the following integrals int (x^(2) + 1)/(x^(4)- x^(2) + 1)dx |
|
Answer» |
|
| 10302. |
Solve the following system of linear equations using matrix method.2x-y=-2 3x+4y=3 |
|
Answer» SOLUTION :[[2,-1],[3,4]] [(x),(y)][(-2),(3)] AX=B `|A|=11!=0` `therefore A^(-1)=(adjA)/|A|=1/11[[4,1],[-3,2]]` `X=A^(-1)B` `therefore`x=-5/11,y=12/11` |
|
| 10304. |
The negation ofp to (~p vv q) is |
|
Answer» <P>`p VV (p vv ~Q)` |
|
| 10305. |
If sin^(4)x + cos^(4)y + 2 =4sinx cosy, 0 lt=xy lt=pi/2, then sinx + cosy equals : |
| Answer» Answer :C | |
| 10306. |
Write as a single matrix : (1 - 2 " "3 ) ({:(2,-1,5),(0,2,4),(-7,5,0):})- (2" "- 5 " "7) |
|
Answer» |
|
| 10307. |
If x,y,z are different andDelta = {:[( x,x^(2) , 1+x^(3)),( y,y^(3) ,1+y^(3)),( z,z^(3) ,1+z^(3)) ]:} |
|
Answer» |
|
| 10308. |
The maximum value of Z = x + 4y subject to the constraints 3x+6y le 6, 4x+8y ge 16, x ge 0, y ge 0 is ……… |
| Answer» Answer :D | |
| 10310. |
The loucs of the point of intersection of the tangents to the circle x=4 cos theta, y=4 sin theta at the points whose parametric angles differ by (pi)/3 is |
|
Answer» `x^(2)+y^(2)=r^(2)` |
|
| 10311. |
{:("Column A" , "The population of a country increases at a fixed percentage each year","ColumnB"),("Increase in population in the first decade 1980-1990",,"Increase in population in the second decade 1990-2000"):} |
|
Answer» If COLUMN A is LARGER |
|
| 10312. |
A single die is rolled twice in succession. What is the probability that the number showing on the second toss is greater than that on the first rolling? |
|
Answer» |
|
| 10313. |
Resolve (x^(4)+24x^(2)+28)/((x^(2)+1)^(3))into Partial fractions. |
|
Answer» |
|
| 10314. |
If 1/(sqrt(20111+sqrt(2011^2-1)))=sqrtm-sqrtnwhere m and n are positive integers , what is the value of m + n. |
|
Answer» |
|
| 10315. |
If A,G,H be the arithmetic, geometric and harmonic means, respectively, of two different natural numbers, then |
|
Answer» `AgtHgt G` |
|
| 10316. |
Show that A=[{:(5,3),(-1,-2):}]satisfies the equation A^(2)=3A-7I=0and hence find A^(-1). |
|
Answer» |
|
| 10317. |
If g be a differentiable function stisfying intg(x)dx=g(x)+c, then lim_(xrarr-2)f[g(x)]^(2) is equal to |
| Answer» Answer :C | |
| 10318. |
If x -iy = sqrt([(a - ib)/(c-id)]) , then (x^(2) + y^(2))^(2) = |
|
Answer» `((a^(2) + B^(2)))/((C^(2) - d^(2)))` |
|
| 10319. |
Four small square on a chess board are selected at random. Find the probability that they form a square of the size 2 xx 2 |
|
Answer» |
|
| 10320. |
A double convex lens made of glass (mu=1.5) is immersed in water (mu=4//3). If its focal length in air is 'F', then the focal length in water will be : |
|
Answer» Solution :`(1.5-1)((1)/(R_(1))-(1)/(R_(2)))=(1)/(F)` `((1.5)/(4)xx3-1)((1)/(R_(1))-(1)/(R_2))=(1)/(F)` `(0.5)/(0.5)xx4=(F')/(F)rArrF'=4F""]` |
|
| 10321. |
A card is drawn from a pack at random. After noting the card it is replaced and the pack is well shuffled . Again if a card is drawn , the probability of getting a card of clubs in the first draw and not a queen card in the second draw is |
|
Answer» `3//13` |
|
| 10322. |
Prove that the height of a right circular cylinder of given volume and maximum total surface is equal to the diameter of its base. |
| Answer» | |
| 10323. |
a xx (b xx c), b xx (c xx a, c xx (a xx b) are |
|
Answer» coplanar |
|
| 10324. |
A bag (I) contains 4 white and 2 black balls and bag II contains 3 white and 4 black balls. One bag is selected at random and one ball is drawn from it. Then find the probability of an event that selected ball is white. |
|
Answer» |
|
| 10325. |
For the final challenge, Bowser asks, “For which integers n, does there exist a shape which can be tiled using 2 × 1dominoes in exactly n different ways?” |
|
Answer» All NATURAL Numbers  This CONSTRUCTION can actually be generalised to any n. For n = 5 we havethe following shape (with four holes). 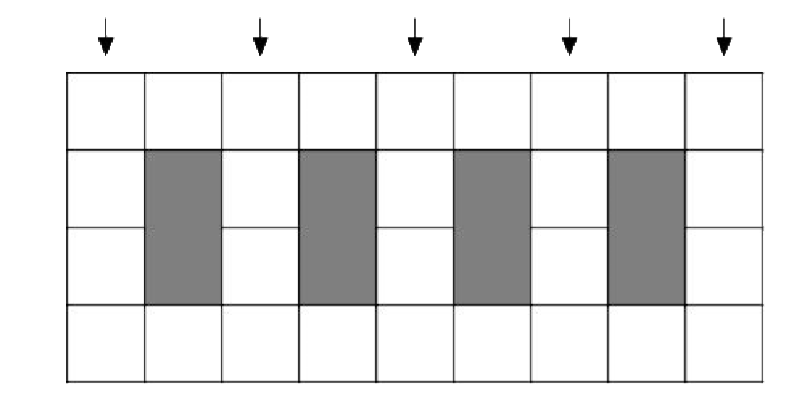 Call a column strong if it has two vertical dominoes. Out of the five columnsindicated, at least one must be strong. But as soon as we CHOOSE a strongcolumn, the tiling is forced and no other columns can also be strong. Forexample, if the fourth column is strong, the following tiling is forced. 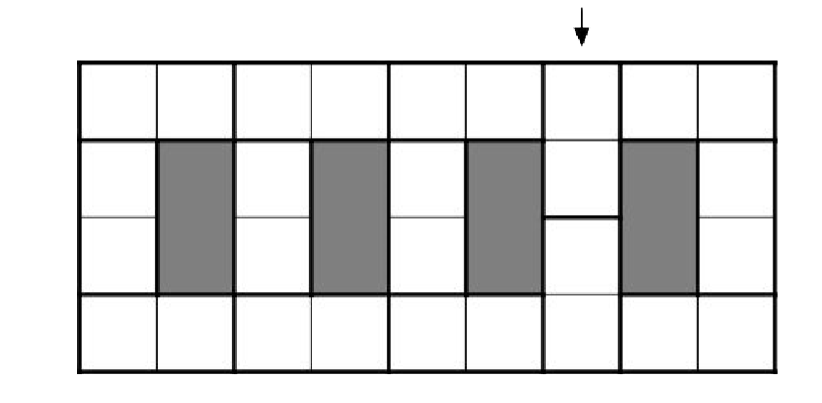 Since there were five POSSIBLE choices of strong columns, there are exactlyfive ways to tile the shape. By similar arguments, for all natural numbers n,there exists a shape which can be tiled by dominoes in exactly n ways. |
|
| 10326. |
Letf(x)bea continuousfunction for allx in R and f'(0) =1 then g(x)= f(|x|)= f(|X|)-sqrt((1-cos2x)/(2)), at x=0, |
|
Answer» is differentiableat x=0 ANDITS valueis 1 |
|
| 10327. |
If the productof twoof theroots ofx^3 +kx ^2 -3x+4=0 is-1thenk= |
|
Answer» `7/2 ` |
|
| 10328. |
Ifcos x + cot x +1=cosec x then the possible values ofx can be |
|
Answer» STATEMENT -1 is truestatement-2 is true statement 2is acorrect explananationfor statement -1 |
|
| 10329. |
Assertion (A) : Lt_(x to 0)(|x|)/(x)=1 Reason (R) : Limit of a function doesn't exist if left and right limits exists and are not equal the correct answer is |
|
Answer» Both A and R are TRUE and R is the CORRECT EXPLANATION of A |
|
| 10330. |
If f(x)=(1)/(x+1)+(1)/(2(x+1)^(2))+(1)/(3(x+1)^(3))+…(x gt 1)and f(1), f(2), f(3) are respectively p, q, r then their ascending order is |
|
Answer» <P>p, Q, R |
|
| 10331. |
Find the equation of the parabola whose vertex is (3,-2) and focus is (3,1). |
|
Answer» |
|
| 10332. |
If |z-4 +3i| le 2then the least and the greatest values of |z| are q |
|
Answer» 3,7 |
|
| 10333. |
LetP(n) : 2^n lt(1 xx 2 xx 3 xx ….xx n). Thenthe smallestpositive integersforwhichP(n )istrue, is |
|
Answer» 1 |
|
| 10334. |
Let f:R rarr R be a function defined by f(x+1)=(f(x)-5)/(f(x)-3), forall x in R. Then, which of the following statements is/aretrue? |
|
Answer» F(2008)=f(2004) |
|
| 10335. |
If -5c-7 le 8, what is the least possible value of 15c+7 ? |
|
Answer» `-38` |
|
| 10336. |
Write the piecewise definition of the following functions. (i) f(x)= [sqrt(x)] "(ii) " f(x)=[tan^(-1)x] "(iii) " f(x)=[log_(e)x] In each case [.] denotes the greatestinteger function. |
|
Answer» Solution :(i)`f(x)=[sqrt(x)], x ge 0.` `[sqrt(x)]=0 " if " sqrt(x) in[0,1) " or " x in [0,1)` `[sqrt(x)]=1 " if " sqrt(x) in[1,2) " or " x in [1,4)` `[sqrt(x)]=2 " if " sqrt(x) in[2,3) " or " x in [4,9)` and so on. ` :. f(x) ={(0"," x in[0,1)),(1"," x in[1,4)),(2"," x in[4,9)),(3"," x in[9,16)),(...),(...):}` (ii) `f(x)=[tan^(-1)x]` We KNOW that `tan^(-1)x in(-(pi)/(2),(pi)/(2))` ` :. " possible values of " [tan^(-1) x]" are " -2,-1,0,1.` If `[tan^(-1)x]= -2," then " tan^(-1)x in (-(pi)/(2),-1) " or " x in (-oo,-tan1) ` If `[tan^(-1)x]= -1," then " tan^(-1)x in [-1,0) " or " x in [-tan1,0) ` If `[tan^(-1)x]= 0," then " tan^(-1)x in [0,1) " or " x in [0,tan 1) ` If `[tan^(-1)x]= 1," then " tan^(-1)x in [1,(pi)/(2)) " or " x in [tan 1, oo) ` (III) `f(x) =[log_(e)x]` We know that `log_(e) in (-oo,oo)`. ` :. [log_(e)x] in Z," i.e., " [log_(e)x]` TAKES all integral values. If `[log_(e)x] =N,n in Z " then " log_(e)x in [n,n+1) " or " x in [e^(n),e^(n+1))`. Therefore, `[log_(e)x]={(...),(...),(-1"," x in[e^(-1),1)),(0"," x in[1,e)),(1"," x in[e,e^(2))),(2"," x in[e^(2),e^(3))),(3"," x in[e^(3),e^(4))),(...),(...):}` |
|
| 10337. |
If C_(r) denotes the binomial coefficient .^(n)C_(r ) then (-1) C_(0)^(2) + 2C_(1)^(2) + 5C_(2)^(2) +….+(3n-1) C_(n)^(2) = |
|
Answer» `(3n-2) .^(2n)C_(N)` |
|
| 10338. |
If the chords of contact of tangents from two points to the ellipse are a right angles, then show that (x_(1)x_(2))/(y_(1)y_(2))=-(a^(4))/(b^(4)) |
|
Answer» `-16` |
|
| 10339. |
Maximum value of6+4x-4x^(2) is |
|
Answer» 6 |
|
| 10340. |
A firm suffers a loss of Rs 144 if one of its special products does not sell. The original revenue is approximated by MR = 27-5x and marginal cost by MC = 4x - 27. Determine the profit function. |
|
Answer» |
|
| 10341. |
If alpha ,beta,gamma are the roots of x^3 -7x +6=0then find the equation whose roots are (alpha-beta)^2 ,(beta-gamma)^2,(gamma-alpha)^2 |
|
Answer» `x^(3) - 42X^(2) + 441x - 400 = 0 ` |
|
| 10342. |
If the complex numbers sinx+icos 2x and cosx-isin2x are conjugate of each other, then the number of values of x in the inverval [0, 2pi) is equal to (where, i^(2)=-1) |
|
Answer» 0 |
|
| 10343. |
If [x] denote the greatest integer function , then , int_(0)^(pi//6) (1 - cos 2x)/(1 + cos 2x) d(x - [x]) = |
|
Answer» `(1)/(SQRT(3))+ (pi)/(6)` |
|
| 10344. |
f: R rarrR be defined by f(x) =x/2+3, g: R rarr Rbe defined by g(x) = 2x-K. If fog = gof then find the value of K. |
|
Answer» |
|
| 10346. |
For the non-zero vectors veca, vecb and vecc, veca.(vecbxxvecc) = 0 if |
|
Answer» `vecbbotvecc` |
|
| 10347. |
If x and y are connected parametrically by the equations, without eliminating the parameter, Find (dy)/(dx). x= a(cos t+ log tan (t)/(2))y= a sin t. |
|
Answer» |
|
| 10348. |
If x and y are connected parametrically by the equations, without eliminating the parameter, Find (dy)/(dx). x= a(theta-sin theta), y= a (1+ cos theta). |
|
Answer» |
|
| 10349. |
If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find (dy)/(dx). x= cos theta-cos 2theta, y= sin theta-sin 2theta. |
|
Answer» |
|
| 10350. |
Evaluation of definite integrals by subsitiution and properties of its : f is a function such that f'(x)=f(x) and f(0)=1g(x) is a function such that g(x)+f(x)=x^(2) then int_(0)^(1)f(x)g(x)dx=……… |
|
Answer» `(1)/(4)(e-7)` |
|