InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10351. |
If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find (dy)/(dx). x= 2at^(2), y= at^(4). |
|
Answer» |
|
| 10352. |
Determine the shortest distance between the following lines and conclude whether they intersect or not (i) vec(r)=(hat(i)-hat(j))+t(2hat(i)+hat(k)),vec(r)=(2hat(i)-hat(j))+s(hat(i)-hat(j)-hat(k)) (ii) (x-1)/(2)=(y+1)/(3)=(z-0)/(1),(x+1)/(5)=(y-2)/(1),z=2 |
|
Answer» |
|
| 10353. |
Without expandingthe determinant prove the following. |[x,a,x+a],[y,b,y+b],[z,c,z+c]|=0 |
|
Answer» Solution :`|[X,a,x+a],[y,b,y+a],[Z,C,z+a]|=|[x+a,a,x+a],[y+b,b,y+b],[z+c,c,z+c]|`(by`C_1rarrC_1+C_2`) `=0(becauseC_1=C_3)` |
|
| 10355. |
Let there are 4 sections of 25 students each in a coaching class. Now, out of 150 students 100 are to be selected randomly and entrolled in these sections. Then, the probability that the students A and B (both present in 150 students) are selected and placed in the same section, is |
| Answer» Answer :B | |
| 10356. |
Evaluate the definite integrals int_(0)^(pi/2)sin2xdx |
| Answer» | |
| 10357. |
Let f(x)={(1-|x|","|x|le1),(0","|x|gt1):} and g(x)=f(x-1)"for all" x in R The graph for g(x) is given by |
|
Answer»
|
|
| 10358. |
How many grams of benzene would be produced when 135.5 gms of phenyl magnesium chloride is trated with 224 ml of ethyne at STP ? |
Answer» Solution :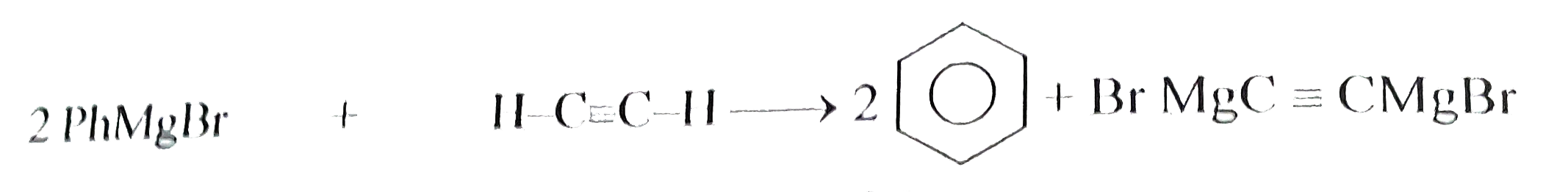 `{:("2 MOLES",22.4Ldarr,"2 Moles",),(,"LIMITING reagent",=156"GMS",):}` `because22400mlH-C-=-H" gives=156 gms of BENZENE"` `:.1mlH--=C-H" gives"=(156)/(22400)xx224=1.56" GM of Benzene"` `:.224mlH-C-=-H"gives =1.56 gms"]` |
|
| 10359. |
If for 5 observations of pairs (x,y), Sigmax=15,Sigmay=25,Sigmay^(2)=135 and Sigmaxy=83, then the value of b_(xy) is |
|
Answer» 0.8 |
|
| 10360. |
Consider the equation sinx=k, k being a parameter lying in the inverval [-1,1]. Statement-1 : For given k, the equation sinx=k has two solutions in [0,2pi] Statement-2 : sintheta=kiffsin(pi-theta)=k. |
|
Answer» Statement-1 is TRUE, statement-2 is true, statement-2 is a CORRECT EXPLANATION for statement-8 |
|
| 10361. |
Variance (sigma^(2)) and thecoefficient of variation (CV) of two distributions are given below. (i) Compute the standard deviations of the given distributions.(ii) What are their means? |
|
Answer» |
|
| 10362. |
Which of thefollowing reactions is not involved in extraction of Cu from copper pyrite ? |
|
Answer» `Cu_(2)S * Fe_(2)S_(3) +4O_(2) rarr Cu_(2)S+2FeO+3SO_(2)uparrow` |
|
| 10364. |
A circle C is drawn on the line joining the centres of the circles C _(1) :x ^(2) +y ^(2) -4 =0 and C _(2): x ^(2) +y ^(2) -8x + 7=0as a diameter. The length of the intercept made on the common chord of the circles C_(1) and C_(2) by the circle C is |
| Answer» Answer :B | |
| 10365. |
Simplify: cot^(-1)""(1)/(sqrt(x^(2)-1))"for" c lt-1. |
|
Answer» |
|
| 10366. |
IfDelta = {:|( a_11, a_12, a_113),( a_21,a_22,a_23) ,(a_31,a_32, a_33) |:} and Aij is Cofactors of a_ijthen value of Deltais given by |
|
Answer» ` a_11 A_31+ a_12A_32+a_13A_33` |
|
| 10367. |
If the normals at t_(1) andt_(2) on y^(2) = 4ax meet again on the parabola then t_(1)t_(2)= |
| Answer» ANSWER :C | |
| 10368. |
Let f _(a)(x) =In x andfor n ge 0 and x gt 0 Let f _(a)(x) = int _(0) ^(x)f _(a) (t) dt then: Value of lim _( x to oo) ((lfloorn )f _(n)(1))/(ln (n)): |
| Answer» ANSWER :C | |
| 10369. |
Evaluate the following inegrals int sin x sin 2x sin 3x dx |
|
Answer» |
|
| 10371. |
Compute theintegrals I = int_(0)^(5) (dx)/( 2 x + sqrt(3 x + 1)) |
|
Answer» |
|
| 10372. |
A is2 xx 2matrix whose elements are given by a_(ij) = 2 I_(ij) - j .Then find M_(21) +A_(11) , whereM_(ij)is the minor of a_(ij)and A _(ij)is the co-factor ofa_(ij). |
|
Answer» a) 0 |
|
| 10373. |
Findthe area of theregionboundedby linex=2and parabolay^2= 8x |
|
Answer» |
|
| 10374. |
Resolve (2x+3)/((x-1)(x^(2)+x+1)) into partial fractions. |
|
Answer» |
|
| 10375. |
Letalphaandbetabe therootsof thequadraticequationax^2+bx+c=0. Observethe lists givenbelow: Letcorrectmatchof List-IfromList -IIis |
|
Answer» `{:(I,ii,III,iv ),(E,B,D,F):}` |
|
| 10376. |
A triangle is formed by Y-axis, the straight line L passing through the points (3,0)(1, (4)/(3)) and the straight line perpendicular to the line L and passing through the point (8,1). Then, the area of the triangle (in sq units) is |
|
Answer» 16 |
|
| 10377. |
Simplify (1+cosx+isinx)/(1+cosx-isinx). |
|
Answer» |
|
| 10379. |
The probability of guessing correctly atleast 8 out of 10 answers on a true-false type examination is ......... |
|
Answer» `(7)/(64)` |
|
| 10380. |
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective items? |
|
Answer» |
|
| 10381. |
Write{x:x =1 or x=2 or x=3} set in the form of lists? |
| Answer» SOLUTION :`{1,2,3}` | |
| 10382. |
Let A be the area bounded by the curve y=sin x(0 le x le pi) and x-axis and B is the area bounded by the curves y=sin x(0 le x le pi//2), y=a cosx (0 le x le pi//2) and x-axis (a gt0). If A:B=1, then a is equal to |
|
Answer» |
|
| 10383. |
Find the correct pair of statements: (i) The point of intersection of tangents at 't_(1)' and 't_(2) on the parabola y^(2)=4x is (t_(1)t_(2),t_(1)+t_(2)) (ii) Ax^(2)+Bxy+Cy^(2)+Dx+Ey+F=0 represents an ellipse if B^(2)-4ACgt0 (iii) The equation of tangent at (1,-3) to the parabola x^(2)+6x+4y+5=0 is 2x+y+1=0 (iv) Parametric representation of a conic is unique. |
|
Answer» (i) and (III) are CORRECT |
|
| 10384. |
f: R rarr R be defined as f(x) = |x| + |x^(2) -1|. The total number of points at which f attains either local maximum or a level minimum is |
|
Answer» |
|
| 10385. |
Consider the following relations R_(1) = {(x,y) : x and y are integers and x=ay or y=ax for some integer a} R_(2) ={(x,y) : x and y are integers and ax + by =1for some integers a,b},Then |
|
Answer» `R_(1), R_(2)` are not EQUIVALENCE relations |
|
| 10387. |
The differential equation of the family of circles passing through the origin and having their centres on the x-axis is |
|
Answer» |
|
| 10388. |
Let f(x) = {{:((x((3)/(4))^(1//x)-((3)/(4))^(-1//x))/(((3)/(4))^(1//x)+((3)/(4))^(-1//x))",",x ne 0),(0",",x = 0):}. If P = f'(0^(-)) - f'(0^(+)), then 4 (lim_(x rarr p^(-))((exp((x+2)log 4))[(x+1)/(4)]-16)/(4^(x) - 16)), is...... (where [x] denotes greatest integer function.) |
|
Answer» |
|
| 10389. |
If f is any function, then (1)/(2)[f(x)+f(-x)] is always : |
|
Answer» one-one |
|
| 10390. |
Nancy purchased a consignment of c red roses at a cost of d dollars. She made bouquets with the roses and each bouquet contained d roses. She sold each bouquet at a price of c dollars. Overall , she made a profit. {:("Column A" , "","ColumnB"),("Cost (in dollars) of each flower", ,"1 dollar"),("in the consignment", ,):} |
|
Answer» If COLUMN A is larger |
|
| 10391. |
A factory owner purchase two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows : He has an area of 7600 sq.m. available and 72 skilled men who can operate the machines. How many machines of each type should be buy to maximise the daily output ? |
|
Answer» |
|
| 10392. |
Equation of a line passing through the point whose position vector is 2i-3j+4k and in the direction of the vector 3i+4j-5k is |
|
Answer» `4x+3y=17,5y-4z=1` |
|
| 10393. |
The sixth term of an A.P. is equal to 2. The value of the common difference of the A.P. which makes the product a_1 a_4 a_5 least is given by : |
|
Answer» `8/5` =a(a+3d)(a+4d) =(2-5d) (2-2d)(2-d) `P=2(4-16d+17d^2-5d^3)` `P=2(-16 + 34d-15d^2)=0` `d=2/3` and `8/5` For LEAST product d=2/3 |
|
| 10394. |
(1-omega+omega^2)(1-omega^2+omega^4)(1-omega^4+omega^2)….to 2nFactors =2^(2n) |
|
Answer» SOLUTION :`L.H.S.=(1-omega+omega^2)(1-omega^2+omega^4)(1-omega^4+omega^2"…….to 2N FACTORS."` `=(-omega-omega)1-omega^2+omega)(1-omega+omega^2)"……to 2n factors."` `=(-2omega)(-omega^2-omega^2)(-omega-omega)"……to 2n factors"` `=[(-2omega)(-2omega)"………to n factors]"XX[(-2omega^2)(-2omega^2)"......to n factors."]` `=(-2omega)^nxx(-2omega^2)^n=(4omega^3)^n=4^n=2^(2n)`"=R.H.S.(PROVED)" |
|
| 10395. |
If omega ne 1 is a cube root of unity satisfying (1)/(a + w) + (1)/(b + w) + (1)/(c +w) = 2 w^(2) and (1)/(a + w^(2)) + (1)/(b + w^(2)) + (1) /(c + w^(2)) = 2w then the value of (1)/(a + 1) + (1)/(b + 1) + (1)/(c + 1) is |
| Answer» ANSWER :A | |
| 10396. |
Evaluate the integrals in exercise. overset(1)underset(0) int(x)/(x^(2)+1)dx |
|
Answer» |
|
| 10397. |
Let p(n) = (n+1)(n+3) (n+5)(n+7)(n+9) . What is the largest integer that is a divisor of p(n) for all positive even integers n ? |
|
Answer» |
|
| 10398. |
v&=2v-1 {:("Quantity A","Quantity B"),((v&)s,4v):} |
|
Answer» Quantity A is greater. |
|
| 10399. |
If bara and barb are unit vectors and barc satisfies 2(hata times hatb)+barc=hatb times hatc then the maximum value of |(bara times barc).barb| is |
|
Answer» `1/2` |
|
| 10400. |
Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve. |
|
Answer» `(X+y)^(2) = 3XY` |
|