InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 12901. |
Let n in N such that n gt 1. Statement-1: int_(oo)^(0) (1)/(1+x^(n))dx=int_(0)^(1) (1)/((1-x^(n))^(1//n))dx Statement-2: int_a^b f(x)dx=int_(a)^(b) f(a+b-x)dx |
|
Answer» Statement-1 is true, Statement-2 is True,Statement-2 is a correct EXPLANATION for Statement-1. Putting `X^(N)=tan^(2)THETA`, we get `I_(1)=underset(0)overset(oo)int (1)/(1+x^(n))DX=(2)/(n)underset(0)overset(pi//2)int tan^((2)/(n)-1)theta d theta` Putting `x^(n)=sin^(2) theta`, we get `I_(2)=(2)/(n)underset(0)overset(pi//2)int tan^((2)/(n)-1) theta d theta` `:. underset(0)overset(oo)int(1)/(1+x^(n))dx=underset(0)overset(1)int(1)/((1-x^(n))^(1//n)dx` So, statement-1 is also true. |
|
| 12902. |
A=[{:(2,-3),(4,6):}] verify (adjA)^(-1)=(adjA^(-1)) |
|
Answer» |
|
| 12903. |
random variable X has the range {1,2,3,……….}. If P(X=r)=c^(r//r) for r=1,2,3,……… then c= |
|
Answer» `E^(2)` |
|
| 12904. |
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 calories. Two foods X and Y are available at the cost of रु 4 and रु 3 per unit respectively. One unit of the food X contains 200 units of vitamins, 1 unit of minerals and 40 calories, whereas one unit of the food Y contains 100 units of vitamins, 2 units of minerals and 40 calories. Find what combination of X and Y should be used to have least cost, satisfying the requirements. |
|
Answer» |
|
| 12905. |
Consider a binary opertion ** on N defined as a **b=a ^(3) +b ^(3). Choose the correct answer. |
|
Answer» Is `**`both ASSOCIATIVE and COMMUTATIVE ? |
|
| 12906. |
If (0,6) and (0,3) are respectively the vertex and focus of a parabola then its equation is |
|
Answer» `x^2 + 12Y = 72` |
|
| 12907. |
Let a and b be unit vectors inclined at an angle 2alpha(0lealphalepi) each other, then (a+b) lt 1, if |
|
Answer» `ALPHA=(pi)/(2)` ` IMPLIES SQRT(1+12cos 2 alpha )lt 1` ` implies sqrt(2(1+cos 2 alpha ))lt 1` `implies sqrt(4 cos^(2) alpha )lt 1` `implies | cosalpha |lt (1)/(2)` `implies (pi)/(3)lt alpha lt (2pi)/(3) [ :'0 le alpha le pi ]` |
|
| 12908. |
Let A=B B^(T)+C C^(T), where B=[(cos theta), (sintheta)], C=[(sin theta), (-costheta)], theta in R. Then A is : |
|
Answer» `[(0, 0),(0, 0)]` |
|
| 12909. |
Two dice are thrown. If it is known that the sum of numbers on the dice was less than 6, the probability of getting a sum 3, is ......... |
|
Answer» `(1)/(18)` |
|
| 12910. |
Show that the poles of the tangents to the circle x^(2)+y^(2) = a^(2) with respect to the circle (x+a)^(2)+y^(2)=2a^(2) lie on y^(2) +4ax =0 . |
|
Answer» |
|
| 12911. |
If A is symmetric matrix , then B'AB is ……. |
|
Answer» |
|
| 12912. |
If (tanalpha-i[sin(alpha//2)+cos(alpha//2)])/(1+2isin(alpha//2)) is purely imaginary , is |
|
Answer» `npi+pi/4` |
|
| 12913. |
Find a if the coefficients of x^(2) and x^(3) in the expansion of (3 + ax)^(9) are equal. |
|
Answer» |
|
| 12914. |
The mass of a molecule of the compound C_(60) H_(122) is :- |
|
Answer» `1.4 XX 10^(-21) g` |
|
| 12915. |
Let f(x) = [1- x^(2)], x in R, where [] is the greatest integer function. Then |
|
Answer» F is increasing |
|
| 12916. |
If cot^(-1).(n)/(pi)gt(n)/(6),n in N, then the maximum value of n is : |
|
Answer» 6 `rArr""(n)/(pi) LT cot.(pi)/(6)` [as `cot^(-1)x` is a DECREASING function] `rArr""(n)/(pi) lt sqrt3` `rArr""n lt sqrt3pi` `rArr""n lt 5.46` `rArr"MAXIMUM value of n is 5"` |
|
| 12917. |
Let a , b, c be such that b (a + c) ne0. If|{:(a, a+1, a- 1),(-b, b + 1, b- 1),(c, c -1, c+ 1):}| + |{:(a+ 1 , b+ 1,c -1),(a - 1,b - 1, c+ 1),((- 1)^(n+2)a, (-1)^(n+1)b, (-1)^(n) c):}|= 0, then the value of n is |
|
Answer» any INTEGER |
|
| 12918. |
The projection of point P(vecp) on the plane vecr.vecn=q is (vecs), then |
|
Answer» `vecs=((q-vecp.vecn)vecn)/(|vecn|^(2))` `(lamdavecn+vecp).vecn=q` or `LAMDA=(q-vecp.vecn)/(|vecn|^(2))` `impliesvecs=vecp+((vecq-vecp.vecn)vecn)/(|vecn|^(2))` |
|
| 12920. |
OABC is a regular tetrahedron of side unity, then: |
|
Answer» The length of perpendicular from one vertex to opposite face is `SQRT((2)/(3))` |
|
| 12921. |
Using integration find the area of the region bounded by the linesy=1+|x+1| ,x=2 ,x=3 and y=0 |
|
Answer» |
|
| 12922. |
Investigate the following integrals for convergence : (a) int_(0)^(1)(dx)/(sqrt(sinx)), (b) int_(0)^(1)(dx)/(e^(x)-cosx), (c ) int_(0)^(1)(cos^(2)xdx)/((1-x)^(2)), (d) int_(0)^(1)(tanxdx)/(sqrt(1-x^(2))), (e ) int_(1//2)^(6//5)(sinxdx)/(sqrt(|1-x^(2)|)). |
|
Answer» (b) diverges; (c ) diverges; (d) converges; (E ) converges. |
|
| 12923. |
If the normals drawn to the hyperbola xy = 4 at (alpha_(i), beta_(i)) (i = 1,2,3,4) are concurrentat the point (a, b), then ((alpha_(1) + alpha_(2) + alpha_(3) + alpha_(4)))/((beta_(1) + beta_(2) + beta_(3) + beta_(4)))(alpha_(1)alpha_(2)alpha_(3)alpha_(4)) = |
| Answer» Answer :B | |
| 12924. |
i+ 2i^(2) + 3i^(3) + 4i^(4) + …. + 100i^(100) = |
|
Answer» `25( 1 +i)` |
|
| 12925. |
Prove that : Find the 4^("th") term from the end in the expansion (2a+5b)^(8). |
|
Answer» |
|
| 12926. |
Two dice are rolled. Let A be the event of getting sum 10 and B be the event of getting even on both the dice. Find whether A, B are independent or not. |
|
Answer» |
|
| 12927. |
The orbit of the Earth is an ellipse with eccentricity 1/60with the Sun at one of its foci, the major axis being approximately 186 xx 10^(6) miles in length. Find the shortest and longest distance of the Earth from the Sun. |
|
Answer» |
|
| 12928. |
The root of the equation tan^(-1)((x+1)/(x-1))+tan^(-1)((x-1)/(x))=pi-tan^(-1)7 is |
|
Answer» `1/2` |
|
| 12929. |
The three sides of a trapezium are each of length 8 cm . Find the maximum area of the trapezium. |
|
Answer» |
|
| 12930. |
A producer has 20 and 10 unit of labour and capital respectively which he can use to produce two kinds of goods X and Y. To produce one unit of x, 2 units of capital and 1 unit of labour is required. To produce one unit of Y,3 of labour and 1 unit of capital is required. If X and Y are priced at Rs. 80 and Rs. 100 per unit respectively, howshould the producer use his resources to maximise the total revenue? |
|
Answer» |
|
| 12931. |
The vectors of two sides of the triangle are vec(a)=3hati+6hatj-2hatk and vec(b)=4hati-hatj+3hatk then find all the angles of the triangle. |
|
Answer» |
|
| 12932. |
Two braches of a hyperbola |
|
Answer» have a COMMON tangent |
|
| 12933. |
Evaluate : int_((2x)/(1+x^(2)))dx |
| Answer» | |
| 12934. |
If alpha, beta are the roots of the equation x^(2)+x+1=0, then the equation whose roots are alpha^(22)" and "beta^(19), is |
|
Answer» A. `X^(2)-x+1=0` |
|
| 12936. |
A and B are two students. Their chances of solving a problem correctly are (1)/(3) and (1)/(4),respectively. If the probability of their making a common error is (1)/(20)and they obtain the same answer, then the probability of their answer to be correct is .......... |
| Answer» Answer :D | |
| 12937. |
If sin ^(-1) .(2a)/(1+a^(2))+ cosec^(2) (cot ^(-1) 3)=? |
|
Answer» `(a+b)/(1-ab)` |
|
| 12938. |
A,B are conjugate points w.r.t circle having centre O radius r then OA^(2)+OB^(2)-2r^(2)=AB^(2) |
|
Answer» |
|
| 12939. |
Let vec(a), vec(b), vec(c) be three vectors in the xyz space such that vec(a)xxvec(b)=vec(b)xxvec(c)=vec(c)xx vec(a) ne 0 If A, B, C are points with position vector vec(a), vec(b), vec(c) respectively, then the number of possible position of the centroid of triangle ABC is - |
|
Answer» Solution :`vec(a)xxvec(B)+vec(c)xxvec(b)=0` similarly `vec(b)+vec(c)=lambda_(2) vec(a)` `vec(a)+vec(c)=lambda_(1)vec(b)""vec(b)+vec(a)=lambda_(3)vec(c)` 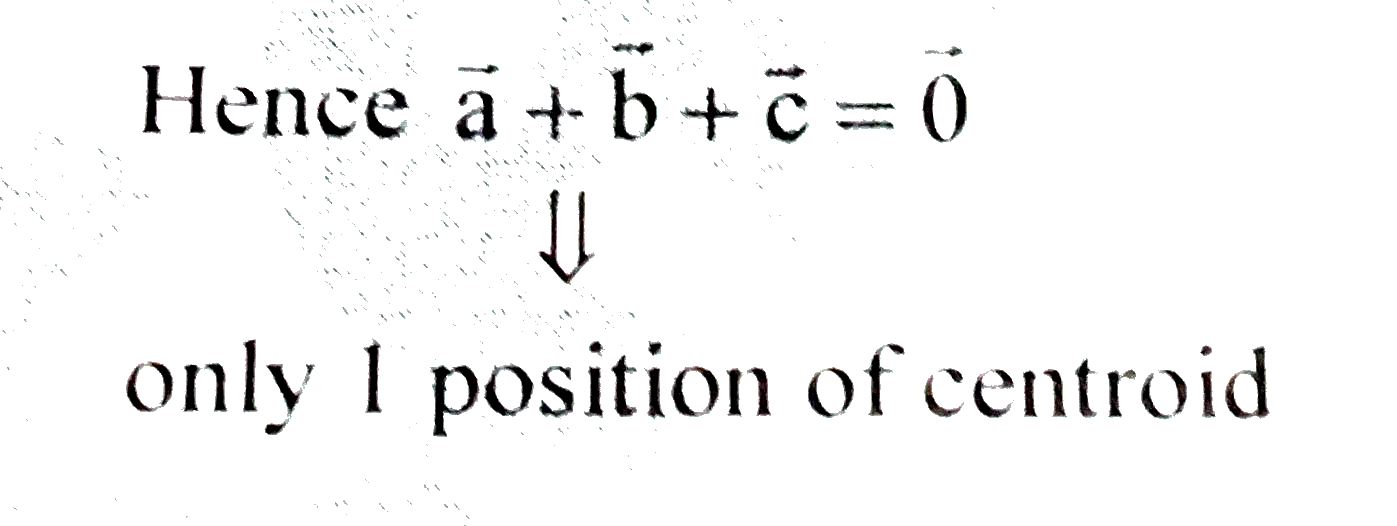
|
|
| 12940. |
If X={8^(n)-7n-1:ninN}andY={49(n-1):ninN}, then |
|
Answer» `XsubY` |
|
| 12941. |
Statement -1 : Ifx in R, x ne 0 , then x^2 + 1/(x^(2)) cannot be equal to cos theta for any theta Statement -2 : Sum of a positive number and its reciprocal cannot be less than 2. |
|
Answer» Statement-1 is TRUE, Statement-2 is True and Statement-2 is a CORRECT EXPLANATION for Statement-1. |
|
| 12942. |
Let alpha, beta be two distinct values of x lying in (0,pi) for which sqrt5 sin x, 10 sin x, 10 (4 sin ^(2) x+1) are 3 consecutive terms of a G.P. Then minimum value of |alpha - beta|= |
|
Answer» `pi/10` |
|
| 12943. |
Compute the integral I_(m,n) = int_(0)^(1) x^(m) (! - x)^(n)dx , where m and n are non-negative integers. |
|
Answer» |
|
| 12944. |
The variance of first 10 multiples of 3 is |
|
Answer» 64.25 |
|
| 12945. |
Let the sum of all divisiors of the form2^(p)*3^(q) (with p, q positive integers) of the number 19^(88)-1 be lambda. Find the unit digit of lambda. |
|
Answer» |
|
| 12946. |
STATEMENT-1 :Ifx is positive , then least value ofx^(12) + (4)/(x^(2)) + (4)/(x)is 9. STATEMENT-2 :Ifa^(2) + b^(2) + c^(2) = 4 , x^(2) + y^(2) + z^(2) = 9then maximum value ofax + by + czis 6 STATEMENT-3 :2 + (3)/(2^(2)) + (4)/(2^(3)) + ......"upto" oo = 4. |
|
Answer» F T F |
|
| 12947. |
Q is a point on the auxiliary circle corresponding to the point P of the ellipse x^2/a^2 + y^2/b^2 =1 If T is the foot of the perpendicular dropped from the focus S onto the tangent to the auxiliary circle at Q then the Delta SPT is |
|
Answer» isosceles |
|
| 12948. |
Differentiate w.r.t x the function sin^(3) x + cos^(6)x |
|
Answer» |
|
| 12949. |
Point of concurrence of the normals drawn at (2,8) , (128,64) , (162, -72)to the parabola y^(2)=32 xis |
|
Answer» A) (`2,8) ` |
|
| 12950. |
If z is a complex number such that z = ln(a – 1) + iln (b – 1) then arg(z) is : |
|
Answer» `PI/4` |
|