28278 + Interview Questions in Maths in Class 12 Page 32 InterviewSolution

1551.	The equation of the circle passing through (1,2) and the points of intersection of the circles x^2+y^2-8x-6y+21=0 and x^2+y^2-2x-15=0 is
Answer» ANSWER :`3(X^(2)+y^(2))-18x-12y+27=0`

Discussion

1552.	If the tangent and normal to a rectangular hyperbola x^(2) -y^(2) =a^(2)cut off interceptsa_1and a_2on one axis andb_1 and b_2on the other then
Answer» `a_1a_2=b_1b_2` `a1b_2=a_2b_1` ` a_1b_2+a_2b_1=0` `a_1a_2+b_1b_2=0` ANSWER :4

Discussion

1553.	If \|[x,2],[18,x]\| = \|[6,2],[18,6]\|, then x =
Answer» `6` `+- 6` `-6` `0` ANSWER :B

Discussion

1554.	In the given figure
Answer» <P>P`to`2, Q`to`4 , R`to`1, S`to`3,5 P`to`4, Q`to`3 , R`to`1, S`to`2 P`to`2, Q`to`2 , R`to`3, S`to`4 P`to`3, Q`to`2,5 , R`to`4, S`to`1 Answer :C

Discussion

1555.	f(x) is a polynomial of degree three with rational co - efficients. If its graph touches the x - axis, then
Answer» f(x) = 0 has no RATIONAL ROOT f(x) = 0 has exactly ONE rational root f(x) has exactly two rational roots f(x) = 0 has exactly THREE rational roots Answer :D

Discussion

1556.	If abs(x) lt 1 then the coefficient of x^(2) in the expansion of (3x)/((x-2)(x+1)) is
Answer» `33/32` `-33/32` `31/32` `-31/32` ANSWER :B

Discussion

1557.	Integration of some particular functions : int x sqrt((1-x^(2))/(1+x^(2)))dx=...+c
Answer» `(1)/(2)[SIN^(-1)X+ sqrt(1-x^(4)]` `(1)/(2)[sin^(-1)x+ sqrt(1-x^(4)]` `sin^(-1)x^(2)+ sqrt(1-x^(4)` `sin^(-1)x^(2)+ sqrt(1-x^(4)` Answer :B

Discussion

1558.	Match the following (##FIITJEE_MAT_MB_07_C02_E04_004_Q01.png" width="80%">{:(A),(B), (C) ,(D):}{:( P,Q,R,S,),(4,3,2,1,),(2,3,4,1,),(3,4,2,1,),( 4,2,3,1,):}
Answer» ANSWER :A

Discussion

1559.	Solve the following different equation (dy)/(dx)+ y sec x= sec x -tan x
Answer» ANSWER :` y (SEC X +TAN x ) =x+c`

Discussion

1560.	Let f: R → R be the Signum Function defined as f(x)={ 1, x>0 0, x=0−1, x
Answer» ANSWER :NO

Discussion

1561.	If a, b, care distinct and the roots of (b-c)x^(2)+(c-a)x+(a-b)=0 are equal, then a, b, c are in
Answer» ARITHMETIC progression Geometric progression Harmonic progression Arithmetico-gemetric progression Answer :A

Discussion

1562.	int(e^(x))/(x+1)[1+(x+1)log(x+1)]dx=......+c
Answer» `(e^(x))/(x+1)` `e^(x)(x+1)` `e^(x)LOG(x+1)` `e^(x)[log(x+1)+1]` ANSWER :C

Discussion

1563.	Statement-1 4^(101) when divided by 101 leaves the remainder4. Statement-2(n^(p) -n)when divided by 'p' leaves remainder zero whenn ge 2, n in Nis a primenumber .
Answer» ANSWER :d

Discussion

1564.	Show that the set A ={-1,0,1} is not closed for addition
Answer» SOLUTION :`-1 N19 A` and -1 in A but (-1)+(-1)=-2 `NE` A

Discussion

1565.	l_(1) and l_(2) are parallel lines, and none of the lines in the figure are vertical. {:("Quantity A","Quantity B"),("The slope of line l, minus the","The slope of line "l_(2)" minus the"),("slope of line "l_(2),"slope of line "l_(2)):}
Answer» QUANTITY A is greater. Quantity B is greater. The TWO QUANTITIES are equal. The relationship cannot be determined from the INFROMATION given. Answer :C

Discussion

1566.	Find thevalues of the following : If sin^(-1)x=y then
Answer» `0leylepi` `-(PI)/2leyle(pi)/2` `0ltyltpi` `-(pi)/2ltylt(pi)/2` ANSWER :B

Discussion

1567.	int_(0)^(pi) cos^(3) x dx =
Answer» -1 0 1 `2sqrt(2)` ANSWER :B

Discussion

1568.	Find a point on the curve y=(x-2)^(2) at which the tangent is parallel to the x-axis .
Answer» ANSWER :POINT is (2,0)

Discussion

1569.	The tangent at a point P on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1, which in not an extremely of major axismeets a directrix at T. Statement-1: The circle on PT as diameter passes through the focus of the ellipse corresponding to the directrix on which T lies. Statement-2: Pt substends is a right angle at the focus of the ellipse corresponding to the directrix on which T lies.
Answer» Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1 Statement-1 is True, Statement-2 is True, Statement -2 is not a correct explanation for Statement-1 Statement-1 is True, Statement-2 is False. Statement-1 is False, Statement-2 is True Solution :The equation of tangents at a POINT P `(x_(1),y_(1))` on the ellipse`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1 " is " ("xx"_(1))/(a^(2))+(yy_(1))/(b^(2))=1`. This cuts the directrix `x=(a)/(e) " at " T((a)/(e),((AE-x_(1))b^(2))/(aey_(1)))` The coordinates of the focus S are (ae, 0). `therefore m_(1)= "Slope of Sp"=(y_(1))/(x_(1)-ae)` and, `m_(2)="Slope of ST " =((ae-x_(1))b^(2))/(aey_(1)(a//e-ae))=(ae-x_(1))/(y_(1))` Clearly, ` m_(1)m_(2)=-1`. So, PT substends a right ANGLE at the focus, Consequently,circle described on PT as a DIAMTER passes through the focus of the ellipse. HENCE, both the statement ar true and Statement -2 is a correct explanation for Statement-1.

Discussion

1570.	if theinequation( sqrt( 8-2x -x^2 ))/(x+10) lesqrt((8-2x -x ^2))/( 2x +9) , thenx liesin
Answer» `[-4,1] CUP{2}` `(-4 ,1]cup{2}` `[-4,1) cup{2}` none Answer :A

Discussion

1571.	One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent? i. E: 'the card drawn is a spade' F: 'the card drawn is an ace' ii. E: 'the card drawn is black' F: 'the card drawn is king' ii. E: 'the card drawn is a king or queen' F: 'the card drawn is a queen or jack'.
Answer» ANSWER :(i), (II)

Discussion

1572.	Using properties evaluate the following definite integrals, evaluate the following:int_0^a sqrtx/(sqrtx+sqrt(a-x)) dx
Answer» Solution :LET I = int_0^a SQRTX/(sqrtx + sqrt(a-X) dx` ___ (a) Then I = `int_0^a sqrt(a-x)/sqrt(a-x)+ sqrt(a-(a-x)) dx` =`int_0^a sqrt(a-x)/(sqrt(a-x)+sqrtx) dx` ____(b) (a)+(b) `GT 2I = int_0^a dx` =`[x]_0^a = a-0 gt I = a/2`

Discussion

1573.	f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also altcltb and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions. If f'(x)gtg'(x)gth'(x), then
Answer» `f(b)ltg(b)lth(b)` `f(b)GTG(b)gth(b)` `f(b)LEG(b)leh(b)` `f(b)geg(b)geh(b)` ANSWER :B

Discussion

1574.	f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also altcltb and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions. If f(b)=g(b)=h(b), then
Answer» `F'(c)=G'(c)=H'(c)` `f'(c)gtg'(c)gth'(c)` `f'(c)LTG'(c)LTH'(c)` None of these Answer :C

Discussion

1575.	f(x) ,g(x), h(x) all are continuos and differentiable functions in [a,b] also altcltb and f(a)= g(a)=h(a). Point of intersection of the tangent at x=c with chord joining x=a and x=b is on the left of c in y= f(x) and on the right in y=h(x). And tangent at x=c is parallel to the chord in case of y=g(x). Now answer the following questions. If c=(a+b)/(2) for each b, then
Answer» `G(x)=AX^(2)+Bx+c` `g(x)=LOGX` `g(x)=sinx` `g(x)=E^(x)` ANSWER :A

Discussion

1576.	Consider f,g and h be three real valued differentiable functions defined on R.Let g(x)=x^(3)+g''(1)x^(3)+(3g'(1)-g''(1)-1)x+3g'(1) f(x)=xg(x)-12x+1 andf(x)=(h(x))^(2),where g(0)=1 The function y=f(x) has
Answer» Exactly one local MINIMA and no local MAXIMA Exactly one local maxima and no local minima Exactly one local maxima and two local minima Exactly two local maxima and no local minima Answer :C

Discussion

1577.	Consider f,g and h be three real valued differentiable functions defined on R.Let g(x)=x^(3)+g''(1)x^(2)+(3g'(1)-g''(1)-1)x+3g'(1)f(x)=xg(x)-12x+1andf(x)=(h(x))^(2), where g(0)=1Which one of the following does not hold good for y=h(x)
Answer» EXACTLY ONE critical POINT No point of inflexion Exactly one real ZERO in (0,3) Exactly one tangent PARALLEL to y-axis Answer :C

Discussion

1578.	For each of the differential equation find the general solution (dy)/(dx) = sin^(-1)x
Answer» ANSWER :`y = x sin^(-1)x + sqrt(1 - x^(2)) + C`

Discussion

1579.	Let each of the circles S_(1)-=x^(2)+y^(2)+4y-1=0 S_(1)-= x^(2)+y^(2)+6x+y+8=0 S_(3)-=x^(2)+y^(2)-4x-4y-37=0 touch the other two. Also, let P_(1),P_(2) and P_(3) be the points of contact of S_(1) and S_(2) , S_(2) and S_(3), and S_(3) , respectively, C_(1),C_(2) and C_(3) are the centres of S_(1),S_(2) and S_(3) respectively. The coordinates of P_(1) are
Answer» `(2,-1)` `(-2,-1)` `(-2,1)` `(2,1)` Solution :`S_(1)-= x^(2)+y^(2)+4y-1=0` `S_(2) -= x^(2)+y^(2)+6x+y+8=0` `S_(3)-=x^(2)+y^(2)-4x-4y-37=0` `C_(1) -=(0,-2),r_(1)=sqrt(5)` `C_(2) -= (-3,(-1)/(2)),r_(2)=(sqrt(5))/(2)` `C_(3)-= (2,2), r_(3)= 3 sqrt(5)` Also,`C_(1)C_(2)=sqrt(9+(9)/(4))=(3sqrt(5))/(2)=r_(1)+r_(2)` So, `S_(1)` and `S_(2)` touch each other externally, `C_(2)C_(3)=sqrt(25+(25)/(4))=(5sqrt(5))/(2)=r_(3)-r_(2)` So, `S_(2)` and `S_(3)` touch each other internally. The point of contact `P_(1)` DIVIDES `C_(1)C_(2)` internally in the ratio `r_(1) : r_(2) = 2:1` `implies P_(1) -= (-2 ,-1)` The point of contact `P_(2)` divides `C_(2)C_(3)` externallyin the ratio `r_(2) : r_(3) = 1:6` `implies P_(2) -= (-4, -1)`. The point of contact `P_(3)` divides`C_(3)C_(1)` externally in the ratio `r_(3) : r_(1) = 3:1` `implies P_(3) -= ( -1,-4)` AREA of `Delta P_(1)P_(2)P_(3)= (1)/(2) \| {:(-2,-1,1),(-4,-1,1),(-1,-4,1):}\| = 3` And area`Delta C_(1)C_(2)C_(3)= (1)/(2) \|{:(0,-2,1),(-3,(-1)/(2),1),(2,2,1):}\|=(15)/(2)` `:. ("area "(Delta P_(1)P_(2)P_(3)))/("area"(DeltaC_(1)C_(2)C_(3)))=(3)/(15)=2:5` Clearly, `P_(2)(-4,-1)` and `P_(3)(-1,-4)` are images of each other with respect to the LINE `y=x`

Discussion

1580.	Let each of the circles S_(1)-=x^(2)+y^(2)+4y-1=0 S_(1)-= x^(2)+y^(2)+6x+y+8=0 S_(3)-=x^(2)+y^(2)-4x-4y-37=0 touch the other two. Also, let P_(1),P_(2) and P_(3) be the points of contact of S_(1) and S_(2) , S_(2) and S_(3), and S_(3) , respectively, C_(1),C_(2) and C_(3) are the centres of S_(1),S_(2) and S_(3) respectively. The ratio ("area"(DeltaP_(1)P_(2)P_(3)))/("area"(DeltaC_(1)C_(2)C_(3))) is equal to
Answer» `3:2` `2:3` `5:3` `2:5` Solution :`S_(1)-= x^(2)+y^(2)+4y-1=0` `S_(2) -= x^(2)+y^(2)+6x+y+8=0` `S_(3)-=x^(2)+y^(2)-4x-4y-37=0` `C_(1) -=(0,-2),r_(1)=sqrt(5)` `C_(2) -= (-3,(-1)/(2)),r_(2)=(sqrt(5))/(2)` `C_(3)-= (2,2), r_(3)= 3 sqrt(5)` Also,`C_(1)C_(2)=sqrt(9+(9)/(4))=(3sqrt(5))/(2)=r_(1)+r_(2)` So, `S_(1)` and `S_(2)` touch each other externally, `C_(2)C_(3)=sqrt(25+(25)/(4))=(5sqrt(5))/(2)=r_(3)-r_(2)` So, `S_(2)` and `S_(3)` touch each other INTERNALLY. The point of CONTACT `P_(1)` divides `C_(1)C_(2)` internally in the RATIO `r_(1) : r_(2) = 2:1` `implies P_(1) -= (-2 ,-1)` The point of contact `P_(2)` divides `C_(2)C_(3)` externallyin the ratio `r_(2) : r_(3) = 1:6` `implies P_(2) -= (-4, -1)`. The point of contact `P_(3)` divides`C_(3)C_(1)` externally in the ratio `r_(3) : r_(1) = 3:1` `implies P_(3) -= ( -1,-4)` Area of `Delta P_(1)P_(2)P_(3)= (1)/(2) \| {:(-2,-1,1),(-4,-1,1),(-1,-4,1):}\| = 3` And area`Delta C_(1)C_(2)C_(3)= (1)/(2) \|{:(0,-2,1),(-3,(-1)/(2),1),(2,2,1):}\|=(15)/(2)` `:. ("area "(Delta P_(1)P_(2)P_(3)))/("area"(DeltaC_(1)C_(2)C_(3)))=(3)/(15)=2:5` Clearly, `P_(2)(-4,-1)` and `P_(3)(-1,-4)` are images of each other with respect to the line `y=x`

Discussion

1581.	Let each of the circles S_(1)-=x^(2)+y^(2)+4y-1=0 S_(1)-= x^(2)+y^(2)+6x+y+8=0 S_(3)-=x^(2)+y^(2)-4x-4y-37=0 touch the other two. Also, let P_(1),P_(2) and P_(3) be the points of contact of S_(1) and S_(2) , S_(2) and S_(3), and S_(3) , respectively, C_(1),C_(2) and C_(3) are the centres of S_(1),S_(2) and S_(3) respectively. P_(2) and P_(3) are images of each other with respect to the line
Answer» `y=x` `y = -x` `y=x+1` `y= -x+2` SOLUTION :`S_(1)-= x^(2)+y^(2)+4y-1=0` `S_(2) -= x^(2)+y^(2)+6x+y+8=0` `S_(3)-=x^(2)+y^(2)-4x-4y-37=0` `C_(1) -=(0,-2),r_(1)=sqrt(5)` `C_(2) -= (-3,(-1)/(2)),r_(2)=(sqrt(5))/(2)` `C_(3)-= (2,2), r_(3)= 3 sqrt(5)` Also,`C_(1)C_(2)=sqrt(9+(9)/(4))=(3sqrt(5))/(2)=r_(1)+r_(2)` So, `S_(1)` and `S_(2)` touch each other externally, `C_(2)C_(3)=sqrt(25+(25)/(4))=(5sqrt(5))/(2)=r_(3)-r_(2)` So, `S_(2)` and `S_(3)` touch each other internally. The point of contact `P_(1)` divides `C_(1)C_(2)` internally in the ratio `r_(1) : r_(2) = 2:1` `IMPLIES P_(1) -= (-2 ,-1)` The point of contact `P_(2)` divides `C_(2)C_(3)` externallyin the ratio `r_(2) : r_(3) = 1:6` `implies P_(2) -= (-4, -1)`. The point of contact `P_(3)` divides`C_(3)C_(1)` externally in the ratio `r_(3) : r_(1) = 3:1` `implies P_(3) -= ( -1,-4)` Area of `Delta P_(1)P_(2)P_(3)= (1)/(2) \| {:(-2,-1,1),(-4,-1,1),(-1,-4,1):}\| = 3` And area`Delta C_(1)C_(2)C_(3)= (1)/(2) \|{:(0,-2,1),(-3,(-1)/(2),1),(2,2,1):}\|=(15)/(2)` `:. ("area "(Delta P_(1)P_(2)P_(3)))/("area"(DeltaC_(1)C_(2)C_(3)))=(3)/(15)=2:5` Clearly, `P_(2)(-4,-1)` and `P_(3)(-1,-4)` are images of each other with RESPECT to the line `y=x`

Discussion

1582.	Determine whether each of the following relations are reflexive, symmetric and transitive : (i) Relation R in the set A= {1, 2, 3, …, 13, 14} defined as "" R = { (x, y ) : 3x - y =0} (ii) Relation R in the set N of natural numbers defined as"" R = {(x, y) : y = x + 5 and x lt 4} (iii) Relation R in the set A= { 1, 2, 3, 4, 5, 6} as ""R = { (x, y) : yis divisible by x} (iv) Relation R in the set Z of all integers defined as "" R = {(x,y) : x -yis an integer } (v) Relation R in the set A of human beings in a town at a particular time given by (a) R= {(x, y) : and y work at the same place } (b) R = { (x, y) : x and ylive in the same locality } (c) R = {(x, y) : xis exactly 7 cm taller than y } (d) R = {(x, y): xis wife of y} (e) R= { (x, y) :xis father of y}
Answer» Solution :(i) A =` { 1, 2, 3, …, 13, 14}` and`"" R = {(x, y) : 3x -y =0}` For reflexive `(x,x) in R AA x in A` but ` "" 3x -y =0rArry =3x` `therfore "" (x, x) notin R ` if ` x = 2 in A` `rArr R `is not reflexive, For symmetricity `(x, y) in R rArr (y, x) in R AA x, y in R ` Now, `"" (x, y) in R rArr 3 x -y =0` `"" rArr 3y -x ne 0` `"" rArr (y, x) notin R` `therefore R` is not symmetric. e.g., `(1, 3) in R and (3, 1) notin R` For transitivity `(x, y) in R, (y, z) in R rArr (x, z) in R` `therefore (1, 3) in R and (3, 9) in R rArr (1, 9) in R` `rArr R` is not transitive. (ii) `R= {(x,y) : y = x + 5 and x lt 4 }` and N is the set of natural numbers. `rArr R = {(1, 6), (2, 7), (3, 8)}` For reflexive, `(1,1) notin R` `rArr R` is not reflexive. For transitivity, `(x,y) in R (y, z) in R rArr (x, z) in R`. No pair satisfies this condition. `therefore R` is not transitive. (iii) `A= {1, 2, 3, 4, 5, 6}` and `R = {(x, y) : y` is divisible by `x}` `rArr R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5, (6, 6)}` For each `x in A, (x, x) in R` `therefore R ` is reflexive. For each `x, y in R, (x, y) in R cancel(rArr) (y, x) in R` `therefore R` is not symmetric. For each `x, y, z in A` if `(x, y) in R, (y, z) in R` then `(x, z) in R` `therefore R` is transitive. (iv) In the set of all integers Z `"" R = {(x, y) : x -y ` is an integer. } Which is true. `therefore R` is reflexive. For symmetricity, `(x, y) in R rArr (x -y)` is an integer. `"" rArr (y-x) in R` ` therefore R` is symmetric. `therefore ` For transitivity. `(x, y) in R and (y, z) in R` `rArr (x -y) ` is an integer and `(y-z)` is an integer. `rArr (x-y)+ (y-z)` is an integer. `rArr (x, z) in R` `therefore R` is transitive. (v) (a) `R= {(x, y) : x and y` work at the same place } This relation is reflexive, symmetric and transitive. (b) `R= {(x, y) : x and y` live in the same locality}. This relation is reflexive, symmetric and transitive. (c) `R= {(x, y) : x` is EXACTLY 7 cmtaller than y } `(x, x) notin R` because x is no exactly 7 cm taller than y `therefore R ` is not reflexive. `(x, y) in R rArrx ` is exactly 7 cm taller than y. `"" cancel ( rArr) y` is exactly 7 cm taller than x. `"" cancel (rArr) (y, x) in R` `therefore R` is not symmetric. `therfore (x, y) in R and (y, z) in R rArr x ` is exactly 7 cm taller than y and y is exactly7 cm taller than z.

Discussion

1583.	Let A,B, and C be three sets such that A={(x,y)\|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"} B= {(x,y)\|(x-3)/(cos phi)=(y-4)/(sin phi)=r} C= { (x,y)\|(x-3)^(2)+(y-4)^(2)leR^(2)} If A capC =A, then minimum value of R is
Answer» 5 6 10 11 Solution :`A= { (x,y)}(x)/(cos theta) =(y)/(sin theta) =5, ` where `theta ` is parameter `}` A is SET of points which lie of the CIRCLE `C_(1) : x^(2)+y^(2) =25` `B = { (x,y)\|(x-3)/(cos phi)=(y-4)/(sin phi) =r}` If` phi` varies and r is fixed, then B is the set of all points which lie on a circle `C_(2) : (x-3)^(2) +(y-4)^(2) =r^(2)` And if `phi` is fixed and r varies, then B is the set of all points which lie on the straight line `L : y-4= tan theta ( x-3)`. Now, if `A cap C =A` Both circle `C_(1)` and `C_(2)` must touch each other internally. So, R must be 10. If `phi` is fixed and r varies and `n ( A cap B) = 1`, circle `C_(1)` touches line L. `phi =90^(@) + alpha` `:. SEC phi = sec ( 90^(@) +alpha)= - cosect alpha = - (5)/(4)`

Discussion

1584.	Let A,B, and C be three sets such that A={(x,y)\|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"} B= {(x,y)\|(x-3)/(cos phi)=(y-4)/(sin phi)=r} C= { (x,y)\|(x-3)^(2)+(y-4)^(2)leR^(2)} If phi is fixed and r varies and (A cap B) =1, then sec phi is equal to
Answer» `(5)/(4)` `(-5)/(4)` `(5)/(3)` `(-5)/(3)` Solution :`A= { (x,y)}(x)/(COS theta) =(y)/(sin theta) =5, ` where `theta ` is parameter `}` A is set of points which lie of the circle `C_(1) : x^(2)+y^(2) =25` `B = { (x,y)\|(x-3)/(cos phi)=(y-4)/(sin phi) =r}` If` phi` varies and r is fixed, then B is the set of all points which lie on a circle `C_(2) : (x-3)^(2) +(y-4)^(2) =r^(2)` And if `phi` is fixed and r varies, then B is the set of all points which lie on the straight line `L : y-4= tan theta ( x-3)`. 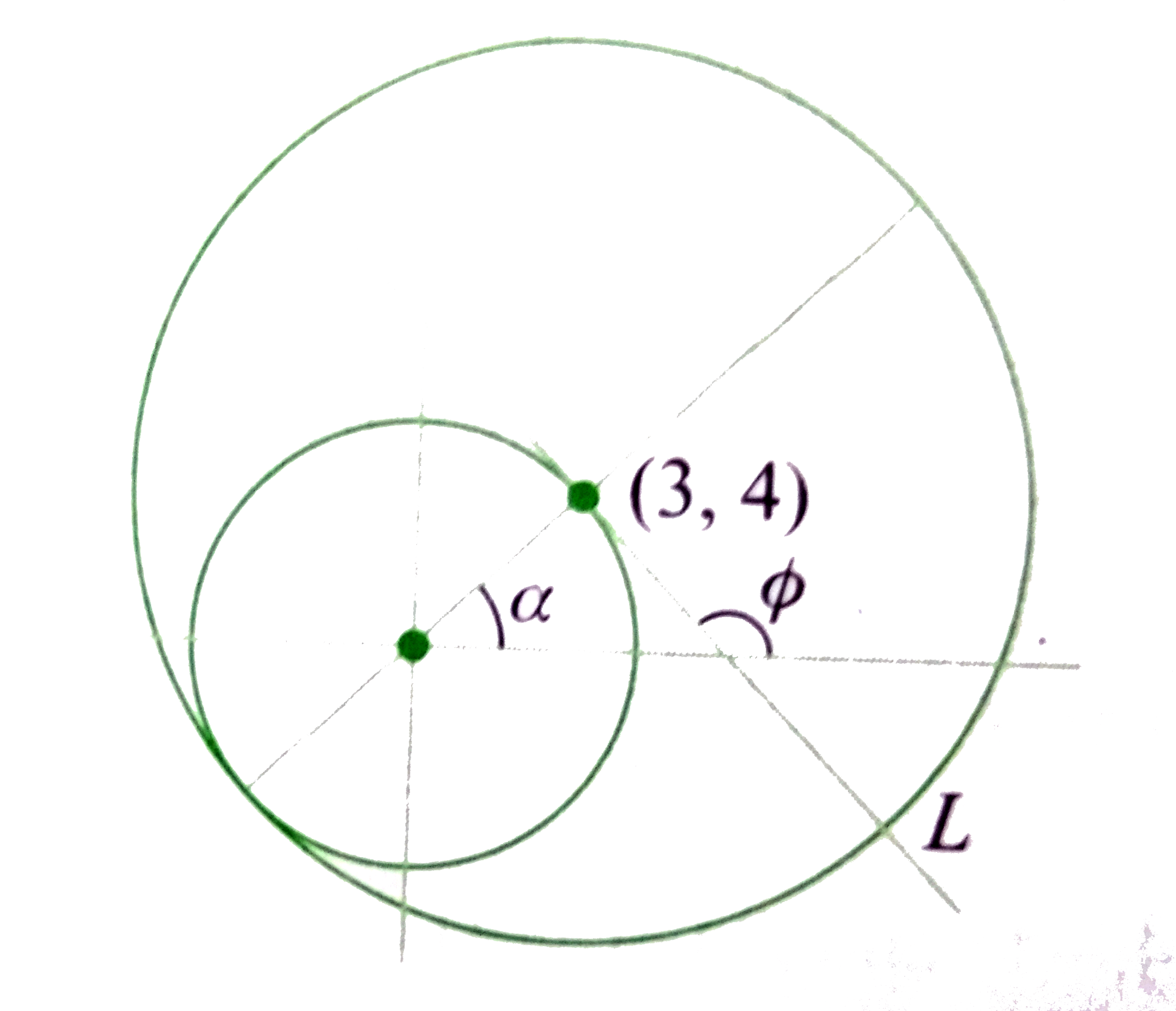Now, if `A cap C =A` Both circle `C_(1)` and `C_(2)` must TOUCH each other internally. So, R must be 10. If `phi` is fixed and r varies and `n ( A cap B) = 1`, circle `C_(1)` touches line L. `phi =90^(@) + alpha` `:. SEC phi = sec ( 90^(@) +alpha)= - cosect alpha = - (5)/(4)`

Discussion

1585.	If tanA=3//4andtanB=-12//5,then how many values cancot (A -B) have depending on the actual values of A and B ?
Answer» 1 2 3 4 Solution :`TANA=(3)/(4)andtanB=-(12)/(5)` `thereforecot(A-B)=(1)/(tan(A-B))=(1=tanAtanB)/(tanA-tanB)`

Discussion

1586.	If p:4 is an even prime number q:6 is a divisor of 12 and r: The HCF of 4 and 6 is 2, then which of the following is true.
Answer» `(p^^q)` `(PVVQ)^^~R` `~(q^^r)VVP` `~PVV(q^^r)` ANSWER :D

Discussion

1587.	For a inR, if \|x - a + 3\| + \|x-3a\|=2x - 4a +3 \| is ture AA x inR.Then find the value of a.
Answer» Solution :`\|x - a + 3\| + \|x-3a\|=2x - 4a +3\|` `rArr\|x - a + 3\| + \|x-3a\|=\|(x - a +3) + (x - 3a)\|` `rArr(x - a + 3 )(x - 3a)ge0 AA x in`R. `rArrx^(2) + x (3 - 4a) + 3a (a - 3) ge 0, AA x in N` R. For the above inequality, `D LE 0` `rArr(3 - 4 a)^(2) - 12 a (a - 3) le 0` `rArr(2a + 3)^(2) le 0` `rArra = - 3//2`

Discussion

1588.	Statmenet 1: The point of intesection of the commonchords of three circles described on the three sides of a triangle as diameter is orthocentre of the triangle. Statement-2 : The common chords of three circles taken two at a time are altitudes of the traingles.
Answer» STATEMENT-1 `:` is True, Statement-2 is True and Statement-2 is a CORRECT explanation for Statement-1 Statement-1 is True, Statement-2 is True and Statement-2 is NOT a correct explanation for Statement -1 Statement-1 is True, Statement-2 is false Statement-1 is False, Statement-2 is True Answer :A

Discussion

1589.	If f (x) =2x, g (x) =3 sin x -x cos x, thenfor x in (0, (pi)/(2)):
Answer» `f (X) gt g (x)` `f (x) LT g (x)` `f (x)=g (x)` has exactly one REAL root. `f (x) =g (x)`has exactly TWO real roots Answer :A

Discussion

1590.	Prove that two vactors are perpendicular iff \|veca+vecb\|^2 = \|veca\|^2 + \|vecb\|^2
Answer» SOLUTION :`\|veca+vecb\|^2 = \|veca\|^2+\|vecb\|^2 ` ` ` ` ` `

Discussion

1591.	Solve the follwing inequations by algebric and graphical methods. i) x^(2) – 8x + 15 gt 0 ii) 2x^(2) + 3x – 2 lt 0 iii) x^(2) - 4x + 5 gt 0 iv) 15x^(2) + 4x – 5 le 0
Answer» Answer :i) `x in (-INFTY, 3) cup (5, infty)` ii) `x in (-2, (1)/(2))` iii) `x in R` iv) `x in [(-2)/(3), (2)/(5)]`

Discussion

1592.	Solution of log ((dy)/(dx)) = 3x+4y, y(0) = 0 is
Answer» `e^(3X) + 3E^(-4y) = 4` `4e^(3x) - e^(-4y) = 3` `3e^(3x) + 4e^(4y) = 7` `4e^(3x) + 3e^(-4y) = 7` Answer :D

Discussion

1593.	Let alpha, beta are two ral roots of equation x ^(2) + px+ q =0, p ,q, in R, q ne 0. If the quadratic equation g (x)=0 has two roots alpha + (1)/(alpha) , beta + (1)/(beta) such that sum of its roots is equal to product of roots, then number of integral values g can attain is :
Answer» ANSWER :3

Discussion

1594.	Find the second order derivatives of the following functions: x^(3) + tan x
Answer» ANSWER :`6X + 2SEC^(2)x TAN x`

Discussion

1595.	Determine which of the following binary operations on the set R are associative and which are commutative : a^(**) b = 1, AA a, b in R
Answer» SOLUTION :N/A

Discussion

1596.	Determine which of the following binary operations on the set R are associative and which are commutative : a^(**)b=((a+b))/2,AAa,binR
Answer» SOLUTION :N/A

Discussion

1597.	int_(0)^(pi//4) tan^(5) x dx=
Answer» `1/2 LN 2 + 1/4` `1/2 ln 2 - 1/4` `1/4 ln 2 - 1/4` `1/2 ln 4` ANSWER :B

Discussion

1598.	Find the area of the parallelogram whose adjacent sides are determined by the vectors veca= hati- hatj+3hatk and vecb= 2 hati-7 hatj+hatk
Answer» ANSWER :`5sqrt(2)` SQUARE UNIT

Discussion

1599.	Integration of some particular functions : int(dx)/(sqrt(21+12x-9x^(2)))=...+c
Answer» `SIN^(-1)((3x-2)/(5))` `3SIN^(-1)((3x-2)/(5))` `(1)/(3)sin^(-1)((3x-2)/(5))` `(1)/(15)sin^(-1)((3x-2)/(5))` Answer :C

Discussion

1600.	Observe the following lists Then the correct matching of solutions of inequalities is
Answer» `{:(A,B,C,D),(1,2,3,4):}` `{:(A,B,C,D),(3,5,1,2):}` `{:(A,B,C,D),(1,3,5,4):}` `{:(A,B,C,D),(3,2,4,1):}` ANSWER :B

Discussion

Explore topic-wise InterviewSolutions in .

The equation of the circle passing through (1,2) and the points of intersection of the circles x^2+y^2-8x-6y+21=0 and x^2+y^2-2x-15=0 is

If the tangent and normal to a rectangular hyperbola x^(2) -y^(2) =a^(2)cut off interceptsa_1and a_2on one axis andb_1 and b_2on the other then

If |[x,2],[18,x]| = |[6,2],[18,6]|, then x =

In the given figure

f(x) is a polynomial of degree three with rational co - efficients. If its graph touches the x - axis, then

If abs(x) lt 1 then the coefficient of x^(2) in the expansion of (3x)/((x-2)(x+1)) is

Integration of some particular functions : int x sqrt((1-x^(2))/(1+x^(2)))dx=...+c

Match the following (##FIITJEE_MAT_MB_07_C02_E04_004_Q01.png" width="80%">{:(A),(B), (C) ,(D):}{:( P,Q,R,S,),(4,3,2,1,),(2,3,4,1,),(3,4,2,1,),( 4,2,3,1,):}

Solve the following different equation (dy)/(dx)+ y sec x= sec x -tan x

Let f: R → R be the Signum Function defined as f(x)={ 1, x>0 0, x=0−1, x

If a, b, care distinct and the roots of (b-c)x^(2)+(c-a)x+(a-b)=0 are equal, then a, b, c are in

int(e^(x))/(x+1)[1+(x+1)log(x+1)]dx=......+c

Statement-1 4^(101) when divided by 101 leaves the remainder4. Statement-2(n^(p) -n)when divided by 'p' leaves remainder zero whenn ge 2, n in Nis a primenumber .

Show that the set A ={-1,0,1} is not closed for addition

l_(1) and l_(2) are parallel lines, and none of the lines in the figure are vertical. {:("Quantity A","Quantity B"),("The slope of line l, minus the","The slope of line "l_(2)" minus the"),("slope of line "l_(2),"slope of line "l_(2)):}

Find thevalues of the following : If sin^(-1)x=y then

int_(0)^(pi) cos^(3) x dx =

Find a point on the curve y=(x-2)^(2) at which the tangent is parallel to the x-axis .

if theinequation( sqrt( 8-2x -x^2 ))/(x+10) lesqrt((8-2x -x ^2))/( 2x +9) , thenx liesin

Using properties evaluate the following definite integrals, evaluate the following:int_0^a sqrtx/(sqrtx+sqrt(a-x)) dx

Consider f,g and h be three real valued differentiable functions defined on R.Let g(x)=x^(3)+g''(1)x^(3)+(3g'(1)-g''(1)-1)x+3g'(1) f(x)=xg(x)-12x+1 andf(x)=(h(x))^(2),where g(0)=1 The function y=f(x) has

Consider f,g and h be three real valued differentiable functions defined on R.Let g(x)=x^(3)+g''(1)x^(2)+(3g'(1)-g''(1)-1)x+3g'(1)f(x)=xg(x)-12x+1andf(x)=(h(x))^(2), where g(0)=1Which one of the following does not hold good for y=h(x)

For each of the differential equation find the general solution (dy)/(dx) = sin^(-1)x

Let A,B, and C be three sets such that A={(x,y)|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"} B= {(x,y)|(x-3)/(cos phi)=(y-4)/(sin phi)=r} C= { (x,y)|(x-3)^(2)+(y-4)^(2)leR^(2)} If A capC =A, then minimum value of R is

Let A,B, and C be three sets such that A={(x,y)|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"} B= {(x,y)|(x-3)/(cos phi)=(y-4)/(sin phi)=r} C= { (x,y)|(x-3)^(2)+(y-4)^(2)leR^(2)} If phi is fixed and r varies and (A cap B) =1, then sec phi is equal to

If tanA=3//4andtanB=-12//5,then how many values cancot (A -B) have depending on the actual values of A and B ?

If p:4 is an even prime number q:6 is a divisor of 12 and r: The HCF of 4 and 6 is 2, then which of the following is true.

For a inR, if |x - a + 3| + |x-3a|=2x - 4a +3 | is ture AA x inR.Then find the value of a.

Statmenet 1: The point of intesection of the commonchords of three circles described on the three sides of a triangle as diameter is orthocentre of the triangle. Statement-2 : The common chords of three circles taken two at a time are altitudes of the traingles.

If f (x) =2x, g (x) =3 sin x -x cos x, thenfor x in (0, (pi)/(2)):

Prove that two vactors are perpendicular iff |veca+vecb|^2 = |veca|^2 + |vecb|^2

Solve the follwing inequations by algebric and graphical methods. i) x^(2) – 8x + 15 gt 0 ii) 2x^(2) + 3x – 2 lt 0 iii) x^(2) - 4x + 5 gt 0 iv) 15x^(2) + 4x – 5 le 0

Solution of log ((dy)/(dx)) = 3x+4y, y(0) = 0 is

Let alpha, beta are two ral roots of equation x ^(2) + px+ q =0, p ,q, in R, q ne 0. If the quadratic equation g (x)=0 has two roots alpha + (1)/(alpha) , beta + (1)/(beta) such that sum of its roots is equal to product of roots, then number of integral values g can attain is :

Find the second order derivatives of the following functions: x^(3) + tan x

Determine which of the following binary operations on the set R are associative and which are commutative : a^(**) b = 1, AA a, b in R

Determine which of the following binary operations on the set R are associative and which are commutative : a^(**)b=((a+b))/2,AAa,binR

int_(0)^(pi//4) tan^(5) x dx=

Find the area of the parallelogram whose adjacent sides are determined by the vectors veca= hati- hatj+3hatk and vecb= 2 hati-7 hatj+hatk

Integration of some particular functions : int(dx)/(sqrt(21+12x-9x^(2)))=...+c

Observe the following lists Then the correct matching of solutions of inequalities is