InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2452. |
A person buys a lottery ticket in 50 lotteries, in ech of which his chance of winning a prize is 1/100. What is the probability that he will a prize (a) exactly once (b) atleast once ? |
|
Answer» |
|
| 2453. |
If k isparameter then the equation of family of lines passing through (3,4) is |
|
Answer» kx-y-4k=0 |
|
| 2454. |
If angle theta between the line (x+1)/(1)=(y-2)/(2)=(z-2)/(2) and the plane 2x-y+sqrt(lambda)z+4=0 is such that sin theta=(1)/(3) then the value of lambda is |
|
Answer» `3//4 ` |
|
| 2455. |
Compute the force of pressure experienced by a vertical triangle with base b and altitude h submerged base downwards in water so that is vertex touches the surface of the water. |
|
Answer» |
|
| 2456. |
If Delta denotes the area of the triangle with vertices (0, 0), (5, 0) and (5/6, 25/6) then Delta is equal to |
|
Answer» |
|
| 2457. |
I. underset(x to oo)"Lt" (sin x)/(x)=1 II. Every identify function is continuous on R. |
|
Answer» only I is true |
|
| 2458. |
If area bouned by x^(3) y + xy^(3) - x^(2) y - xy^(2) = kxy is 0, then the set of value of k is |
|
Answer» `[0, (1)/(4)]` |
|
| 2459. |
The values of A and theta if (1+sin alpha+icosalpha)^8=A(costheta+isintheta) are respectively |
|
Answer» A) `2^8cos^8(pi/4-ALPHA/2),-2ALPHA` |
|
| 2460. |
A right angled isosceles triangle is inscribed in the circle x^(2)+y^(2)-4x-2y-=0 then length of the side of the triangle is |
|
Answer» `SQRT(2)` |
|
| 2461. |
Let D be the domain of a twice differentiable function f. For all x inD,f''(x)+f(x)=0 "and" f(x)=intg(x)dx+"constant". If h(x)={f(x)}^(2)+{g(x)}^(2) and h(0)=5, then h(2015)-h(2014) is equal to |
|
Answer» 5 |
|
| 2462. |
The pair of tangents from (2,1) to the circle x^(2)+y^(2)=1 is |
|
Answer» `3Y^(2)-4xy+16x+8y-20=0` |
|
| 2463. |
Two systems of rectangular axes have the same origin. If a plane cuts them at distances a, b, c and a_1, b_1, c_1respectively from the origin, then a^(-2) + b^(-2) + c^(-2) |
|
Answer» `a_(1)^(-2) + b_(1)^(-2) + c_(1)^(-2)` |
|
| 2464. |
A round table ................. |
Answer» 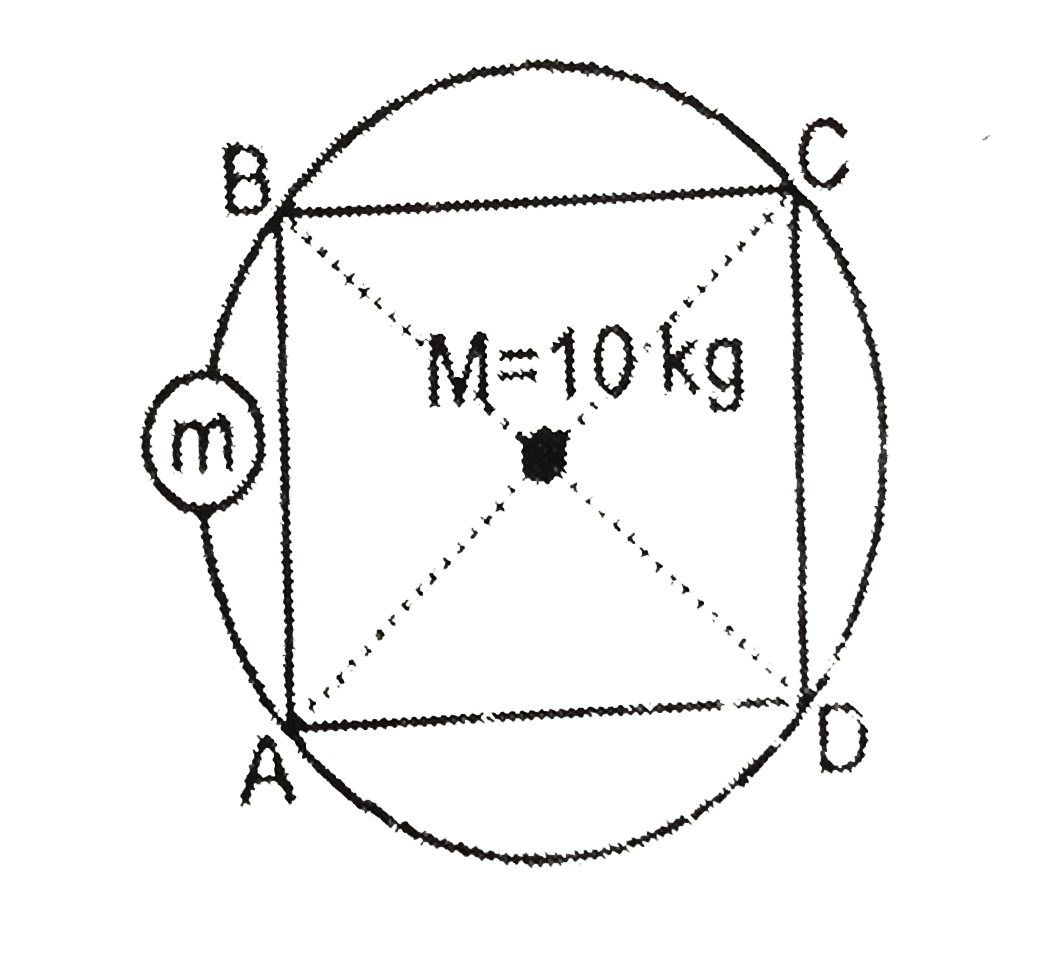 `a/sqrt(2)=R=10` ('a' is the side of SQUARE) `a=10 sqrt(2)` If COM of system is OUTSIDE the square ABCD then table will topple. In the limiting case, taking origin at 'm', `(R-a/2)=(m(0)+MR)/(m+M)` `MXX(R-a/2)=Mxxa/2` `:. m=10/((sqrt(2)-1)) kg` |
|
| 2465. |
The population of a certain city grows at 7% per year, and the current population is 100,000. What will the population of the city be in 10 years ? |
| Answer» SOLUTION :Each year, the population will GROW by a factor of 1.07. Therefore, after 10 years the population will be `100,000(1.07)^(10)~~196,715`. | |
| 2466. |
If the matrix A=[(1,-1),(-1,1)] and A^(2)=kA,then write the value of k |
|
Answer» |
|
| 2467. |
Obtain the following integrals : int(x)/(sqrt(x)+1)dx |
|
Answer» |
|
| 2468. |
If P (A) =6/11,P(B)=5/11and P(AnnB)=7/11,find P(AnnB) |
|
Answer» <P> SOLUTION :`P(ANNB)=P(A)+P(B)-P(AnnB)``RARRP(AnnB)=P(A)+P(B)-P(AnnB)`=6/11+5/11-7/11=4/l1 |
|
| 2469. |
Which one is correct? |
|
Answer» `(1999)^(2000)gt(2000)^(1999)` |
|
| 2470. |
If n is a +ve integer, then the integral part of (4+sqrt(10))^n is an … integer |
|
Answer» odd |
|
| 2471. |
Dimitry bought a pair of pants at the discounted price of $30. The original price of the pants was $40. What was the percent of the discount? |
|
Answer» 0.04 |
|
| 2472. |
Statement I. if alpha beta=-1 then the pair of straight lines x^2-2alphaxy-y^2=0 and y^2+2betaxy-x^2=0 are the angle bisector ofeach other. Statement II. Pair of angle bisector lines of the pair of lines ax^2+2hxy+by^2=0 is h (x^2-y^2)=(a-b)xy. |
|
Answer» STATEMENT I is TRUE, Statement II is true , Statement II is a CORRECT explanationfor Statement I |
|
| 2473. |
Which of the followingis true in a linearprogramming problem ? |
|
Answer» MIN Z= MAX (-z) |
|
| 2474. |
A circle having centre at C is made to pass through the point P(1,2), touching the straight lines7x-y=5 and x+y+13=0 at A and B respectively.Then |
|
Answer» AREA of QUADRILATERAL ACBP is 100 sq. units |
|
| 2475. |
int (3 sinx - 5 cos x )/(7 cos x + 2 sin x )dx = |
|
Answer» `- (29)/(53) x - (31)/(53) `LOG | 7 cos x + 2 SIN x | + c |
|
| 2476. |
If the sum of the coefficients in the expansion of (q+r)^(20)(1+(p-2)x)^(20) is equal to square of the sum of the coefficients in the expansion of [2rqx-(r+q)*y]^(10), where p, r,q are positive constants, then |
|
Answer» ` le P` `=(q+r)^(20)(p-1)^(20)` [put `x=1`] Square of the sum of coefficient of `(2rpx-(r+q)*y^(10)` `=(2rq-(r+q))^(20)` [put `x=y=1`] So `(q+r)^(20)(p-1)^(20)=(2rq-(q+r))^(20)` `impliesp-1=(2rq)/(r+q)-1` `impliesp=(2rq)/(r+q)` `impliesp=H.M.` of `r` and `q` ` le A.M. ` of `r` and `q` `=(r+q)//2` |
|
| 2478. |
STATEMENT-1 :The sum of n terms of two arithmetic progressions are in A.P. in the ratio(7n + 1) : (4n + 17) then the ration^(th) terms is7 :4and STATEMENT-2 :IfS_(n) = ax^(2) + bx = c , "then" T_(n_ = S_(n) - S_(n-1) . |
|
Answer» Statemant-1 is True , Statement-2 is True, Statement -2 is a CORRECT explanation for Statement-1 |
|
| 2479. |
int e^(x) (tan x tan^(2) x ) dx= |
|
Answer» `E^(X) " " tan^(2)` x + C |
|
| 2480. |
Use differential to approximate sqrt36.6. |
|
Answer» |
|
| 2481. |
Let n_(1) "and" n_(2) be the number of red and black balls, respectively, in box I. Let n_(3) "and" n_(4) be the number of red black balls, respectively in box II. One of the two boxes, box 1 and box II was selected at random and a ball was found to be rad. if the probability that this red ball was drawn from box II is 1/3 then the correct option (s) with the possible values of correct option (s) with the possible values of correct option (s) with the possible values ofn_(1),n_(2),n_(3) "and"n_(4) "is (are)" |
|
Answer» `n_(1) = 3, n_(2) = 3, n_(3) = 5, n_(4) = 15` |
|
| 2482. |
Integrate the following int(7)/(2-3x)dx |
|
Answer» SOLUTION :`INT(7)/(2-3x)dx` [PUT 2-3x=t then dx=(-1/3)DT] `(-7/3)int(dt/t)=(-7/3)logabsr+C` (-7/3logabs(2-3x) +C |
|
| 2483. |
If the equation of family of ellipse is x^(2)sec^(2)theta+y^(2)cosec^(2)theta=1, where pi/4ltthetaltpi/2, then the locus of extremities of the latusrectum is |
|
Answer» `2y^(2)(1+x^(2))=(1-x^(2))^(2)` |
|
| 2484. |
Let f : R rarr R be defined as f(x) = 3x. Choose the correct answer. |
|
Answer» f is one - one onto |
|
| 2485. |
Two dice are thrown simultaneously and the sum of the numbers which come up on the dice is noted. Consider the following events A = The sum is even B = The sum is a multiple of 3 C = The sum is less than 4 D = The sum is greater than 11 Which of the following is/are elementary event(s)? |
|
Answer» A and B |
|
| 2486. |
Compute the integral H_(m) = int_(0)^(pi//2) sin^(m) x dx = int_(0)^(pi//2) cos ^(m) x dx (m a natural number) |
|
Answer» |
|
| 2487. |
The separate equations of the lines represented by the equation (x-2)^(2)-3(x-2)(y+1)-3(y+1)^(2)=0 are |
|
Answer» `x-2y-4=0 and x-y-3=0` |
|
| 2488. |
The number of ways of selecting 3 objects from eight object is |
| Answer» | |
| 2489. |
If (1+2x+x^2)^n= sum_(r=0)^(2n) a, x' then a_r= |
|
Answer» `(""^N C_r)^2` |
|
| 2490. |
A = [{:( a,b,c) ,( b,c,a),(c,a,b) :}] if trace (A)= 9 and a,b , c are positive integers such that ab + bc + ca = 26 Let A_1 denotes the adjoint of matrix A , A_2represent adjoint of A_1 …. and so on if value of det ( A_4)is M, then |
|
Answer» `M= 3^(48)` |
|
| 2491. |
Find the number of ways of arranging the letters of the word 'SHIPPING' such that (i) 2 P's will come together |
|
Answer» |
|
| 2492. |
If A+B+C=pi and cosA+cosB+cosC=0=sinA+sinB+sinC then cos3A+cos3B+cos3C= |
|
Answer» 3 |
|
| 2493. |
The sum of the rational terms in the expansion of (sqrt(2) + 3^(1/5))^(10) is |
|
Answer» 41 |
|
| 2495. |
With 4 different elements how many different determinant of order 2 can be constructed. |
|
Answer» COMPLETE DOMINANCE |
|
| 2496. |
Let A be the area of triangle by any tangent to the curve xy=4cosec^(2) theta, theta!=n pi, n epsilon I and the co-ordinate axis. The minimum value of A is: |
|
Answer» `impliesA_(MIN)=8` |
|
| 2497. |
Show that the lines vec(r)= vec(i)+vec(j)-vec(k)+lambda(3 vec(i)- vec(j)) and vec(r)= 4 vec(i)-vec(k)+ mu (2 vec(i) +3 vec(k)) intersect. Also find their point of intersection. |
|
Answer» |
|
| 2499. |
If n (ne 3) is an integer and z = -1 + isqrt3, then z^(2n) + 2^(n) , z^(n) + 2^(2n) = |
| Answer» ANSWER :A | |
| 2500. |
Evaluate the definite integrals int_(1)^(2)(4x^(3)-5x^(2)+6x+9)dx |
|
Answer» |
|