InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2551. |
Let f:NtoNdefined by :f(n)={:{((n+1)/(2) "if n is odd"),((n)/(2) "if n is even"):} |
|
Answer» ONTO but not one-one |
|
| 2552. |
Four numbers are chosen at random (without replacement) from the set {1,2,3,….20}. Statement -1 : The probability that the chosen number when arranged in some order will form an AP is 1/(85) Statement :2 If the four chosen number form an A.P. , then the set of all possiblevalue of common difference is {pm 1, pm 2, pm 3, pm4, pm5} |
|
Answer» Statement -1 is true , statement -2 is true , statement -2 is a correct EXPLANATION for statement -1 |
|
| 2553. |
int_(1)^(10pi)([sec^(-1)x]+[cot^(-1)x])dx, where [.] denotes the greatest integer function, is equal to: |
|
Answer» `10 pi` - SEC1 |
|
| 2554. |
Evaluate : int ((x-2))/({(x+3)^(7)(x-2)^(2)}^(1//3))dx |
|
Answer» |
|
| 2555. |
Find the variance and S.D. of 3,5,7,9,11, 13 is |
|
Answer» |
|
| 2556. |
An analysis or monthly wages paid to the workers of two firms A and B belonging to the same industrygives the following data . (i) Which firm A or B , has greater variability in industrial wages ? (##VIK_MAT_IIA_QB_C08_SLV_015_Q01.png" width="80%"> (i) Which firm A or B , has greater variability in industrial wages ? |
|
Answer» |
|
| 2557. |
Find the position (interior or exterior or on ) of the following points with respect to the parabola y^(2)=6x (i) (2,3) |
|
Answer» |
|
| 2558. |
int_(0)^(3) (3x + 1)/(x^(2)+9)dx= |
|
Answer» `LN (2sqrt(2))+ pi/12` |
|
| 2559. |
If foci of an ellipse are (-2,3),(5,9) & 2x+3y+15=0 is tangent to the ellipse. Then find the point of contact the tangent cannot be |
|
Answer» `((7)/(2),-1)` where `S_(2)^(')` is the point of reflection of `S_(2)` inL. `S_(2)^(')=(-11,-15)` So line joining `S_(1)&S_(2)^(')` is given by `(y-3)=2(x+2)` `y-3=2x+4` `2x-y+7=0` So point `P` will be the point of intersection of `2x-y+7=0&2x+3y+15=0` so point P will be the point of intersection of `2x-y+7=0&2x+3y+15=0` i.e., `(-(9)/(2),-2)` |
|
| 2560. |
Differentiate the following w.r.t. x : cos^(-1) (e^x). |
|
Answer» |
|
| 2561. |
If ais a complex number and b is a real number then the equation bara z + a barz + b = 0 represents |
| Answer» Answer :A | |
| 2562. |
A line with direction cosines proporional to 2,1,2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of' each of the points of intersection are given by |
|
Answer» (3a,3a,3a). (a,a,a) |
|
| 2563. |
If A=|(-1,2,4),(3,1,0),(-2,4,2)|and B=|(-2,4,2),(6,2,0),(-2,4,8)|, then which one of the following is correct ? |
|
Answer» `B=-A` |
|
| 2564. |
Does the following graph pass the vertical or horizontal line test? |
| Answer» Solution :It passes thevertical line test as any VERTICAL line MEETS the graph at one point only. But it not PASS the horizontal test as line y = 1 meets the graph at (2, 1) and (3, 1). HENCE function is many-one. | |
| 2565. |
Differentiate w.r.t.x the function. x^(x)+x^(a)+a^(x)+a^(a), for some fixed a gt 0" and "x gt 0. |
|
Answer» |
|
| 2566. |
Let A = [(-1,2,0),(3,1,5),(-1,2,-1)] then det ((1)/(10)adj (adj A))= ______ |
|
Answer» |
|
| 2567. |
Lattice energy of Na_(2)CO_(3) is -205 kJ/mole and hydration energy of Na^(+) ion & CO_(3)^(2-) ion are -80kJ/mole and -40kJ/mole respectively. What can be predicted about solubility of Na_(2)CO_(3) in water from the above data. |
|
Answer» The SOLUBILITY of `Na_(2)CO_(3)` will increase will increase in temperature 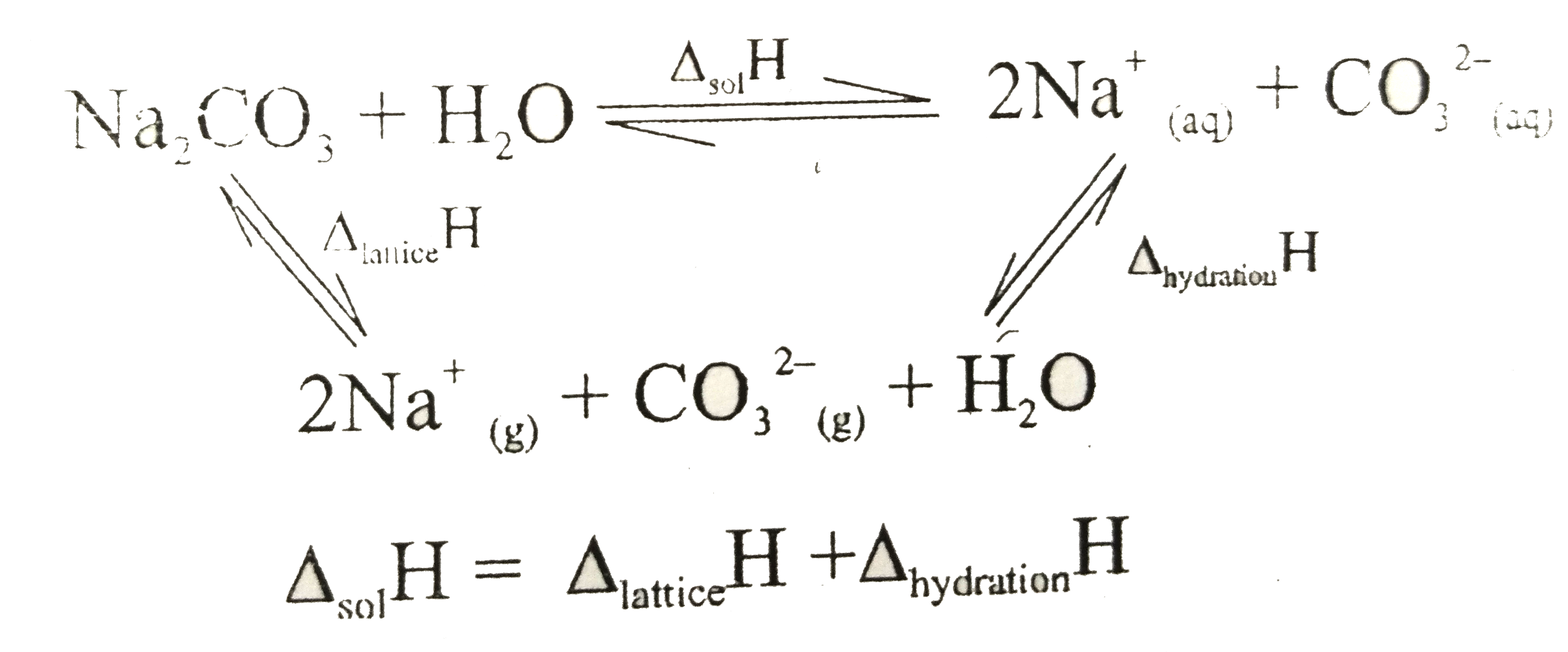 `=205+(-2 xx80-40)` `=+5` `IMPLIES `The process is endothermic So, the solubility will increase with increase in temperature . |
|
| 2568. |
Prove that : Find the coefficient of x^(9) and x^(10) in the expansion of (2x^(2)-(1)/(x))^(20). |
|
Answer» |
|
| 2569. |
Find the vector equation of the plane whose Cartesian from of equation is 3x-4y+2z=5 |
| Answer» Solution :The cartesian equation is 3X - 4y + 2z = 5 The vector equation is = `(3i-4j+2k)=5` | |
| 2570. |
The polynomial P(x)=x^(3)+ax^(2)+bx+c has the property that the mean of its roots, the product of its roots, and the sum of its coefficients are all equal. If the y-intercept of the graph of y=P(x) is 2, The value of P(1) is |
|
Answer» `0` We know that `-a` is the sum of the roots. The average of the roots is equal to the product, so the sum of the roots is `-6`, and `a=6`. FINALLY, `1+a+b+c=2` as well, so we have `1+6+b+2=-2` `impliesb=-11` `:.P(x)=x^(3)+6X^(2)-11x+2` `:.P(1)=1+6-11+2=-2` |
|
| 2571. |
If the normals at (x_(1),y_(1))and (x_(2) ,y_(2)) on y^(2) = 4ax meet again on parabola then x_(1)x_(2)+y_(1)y_(2)= |
|
Answer» `4A^(2)` |
|
| 2572. |
To balance the bicarbonate ion loss in RBC the chloride ions move into RBC, it is known as :- |
|
Answer» Chloride SHIFT |
|
| 2573. |
Let f(x) be an even function with period 2 and f(x) be integrableon every interval . If g(x)= int_(0)^(x) f(t) dt, then g(x+2)= |
|
Answer» `G(X)g(2)` |
|
| 2574. |
There are 20 points in a plane of which 5 are collinear and no three of the points are collinear unless all the three are from these 5 points. Find the number of different lines formed. |
|
Answer» |
|
| 2575. |
(1)/(4)+(1)/(3)((1)/(4))^(3)+(1)/(5)((1)/(4))^(5)+…..oo=……. |
|
Answer» 4 log3 |
|
| 2576. |
(1 - omega) (1 - omega^(2)) (1 - omega^(4)) (1 - omega^(5)) (1 - omega^(7)) (1 - omega^(8)) = |
|
Answer» 25 |
|
| 2577. |
ABC is any triagnel inscribedin the circle x^(2)+y^(2)=r^(2) such that A is fixed point . If the external and internal bisectors of /_A intersect the circle at D and E, respectively, then which of the following statements is true Delta ADE? |
|
Answer» Its centroid is a fixed point. 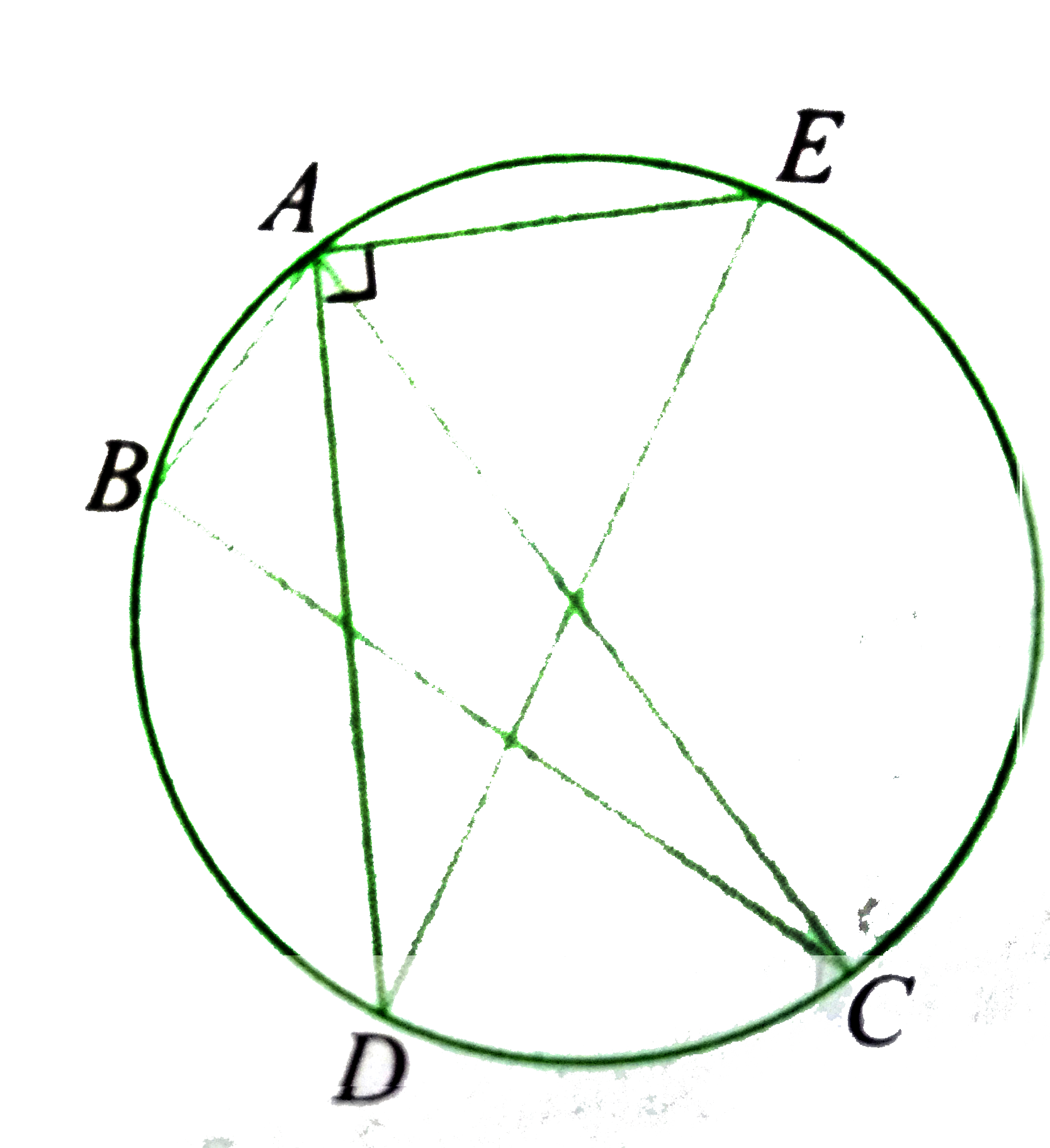 Orothocentre of `DELTA ADE ` is A itself circumcentre is at origin. HENCE, centroid is also a fixed point. |
|
| 2578. |
If vec(beta) is perpendicular to both vec(alpha) and vec(lambda) where vec(alpha)=hat(k) and vec(lambda)=2hat(i)+3 hat(j)+4 hat(k), then what is vec(beta) equal to ? |
|
Answer» `3HAT(i)+2hat(J)` Since `vec(beta).vec( ALPHA)=0 and vec(beta).vec(lambda)=0` `:. C=0 and 2a + 3b=0 rArr a = - (3b)/(2)` Hence, `vec(beta)=-(3 b)/(2) vec(i)+b hat(j)=0 rArr -3 hat(i)+2 hat(j)=0` |
|
| 2579. |
If x and y are uncorrelated variables and if U=x+y and V=x-y, then e(u,v) is equal to |
|
Answer» `(SIGMA X^(2)+sigma^(2))/(sigma x^(2)-sigmay^(2))` |
|
| 2580. |
Ifcos alpha + cos beta + cos gamma = 0= sin alpha + sin beta + sin gammathen show thatcos 3 alpha + cos 3 beta + cos 3 gamma = 3 cos ( alpha + beta + gamma) |
| Answer» | |
| 2581. |
The maximum slope of the tangent to the curve y = e^(x) sin x, x in [0, 2pi] is at: |
|
Answer» `X = (PI)/(4)` |
|
| 2582. |
Formthe polynomialwithrationalcoefficientswhoserootsare 1+ 5i ,5-i |
|
Answer» |
|
| 2583. |
Using differentials, find the approzimate value of each of the following up to 3 places of decimal :(401)^((1)/(2)) |
|
Answer» |
|
| 2584. |
int(1)/(sqrt(sin^(3)xsin(x+alpha)))dx is equal to |
|
Answer» `2"COSEC "alphasqrt(cosalpha+sin alphatanx)+C` |
|
| 2585. |
The solution of the differential equation"dy"/"dx"=x/(2y-x) is |
|
Answer» `(x-y)(x+2y)^2=C ` |
|
| 2586. |
Find the probability of getting sum atmost 10 when two dice are rolled. |
|
Answer» |
|
| 2587. |
Theshortest distance betweencurves (x^(2))/(32)+(y^(2))/(18) =1 " and "(x+(7)/(4))^(2)+y^(2)=1 |
|
Answer» 15 |
|
| 2589. |
Solve the equation z^7=1 |
|
Answer» Solution :`z^7=1=COS 0+ SIN 0` `=cos(0+2kpi+isin 2kpi)` `=cos 2kpi+isin 2kpi` `:.z=(cos 2kpi+isin 2kpi)^(1/7)` `=cos (2kpi)/7)+isin(2kpi)/7)` `"where"k=0,1,2,3,4,5,6` |
|
| 2590. |
The solution set of sin 3theta + cos 2theta -2=0 is |
|
Answer» `{x|x= (npi)/3 +(-1)^(N+1) pi/6} cap {x|x=npi +-pi/2} n inI` |
|
| 2591. |
If (d)/(dx)f(x)=cos x +sin x and f(0)=2, then f(x)=..... |
|
Answer» `x sin x` |
|
| 2592. |
Concider the function defined on [0,1] rarr R f(x) =(sinx- cosx)/(x^(2)), if x ne 0 and f(0) =0 lim_(t rarr 00)(1)/(t^(2) int_(0)^(t) f(x) dx is equal to |
|
Answer» `1//3` |
|
| 2594. |
cos ^(2) ((pi)/(6) +thet a) -sin ^(2) ((pi)/(6) -theta) is equal to |
|
Answer» `1/2 COS 2 THETA ` |
|
| 2595. |
A plane meets the axes in the points, A, B and C. If the centroid of Delta ABC is (alpha,beta, gamma) then the plane is ............... |
|
Answer» `X/ALPHA + y /BETA + z/gamma = 3` |
|
| 2596. |
Three non-coplanar vector a, b and c are drawn from a common initial point. The angle between the plane passing through the terminal points of these vectors and the vector a times b+b times c+c times a is |
|
Answer» `pi//4` |
|
| 2597. |
For an angle with measure alpha in a right triangle, sin alpha = 40/41 and tan alpha = 40/9. What is the value of cos alpha ? |
|
Answer» `9/41` |
|
| 2598. |
Find all solution (x_(1),x_(2),x_(3),......x_(n)) of the equation: 1+1/x_(1) + (x_(1)+1)/(x_(1)x_(2)) + ......... + ((x_(1)+1)(x_(2)+1)....(x_(n+1)+1))/(x_(1)x_(2)......x_(n))=0 |
|
Answer» |
|
| 2599. |
If cos 5theta=a cos theta+ b cos^(3) theta+c cos^(5)theta+d, then |
|
Answer» `a=20` |
|
| 2600. |
L is a line passing through the origin and making an angle theta with the positive direction of x-axis. L_(n) is a line perpendicular to L at a distance n from the origin. L_(n) meets x-axis at A_(n). Distance of A_(n) from the origin O is d_(n). If the geometric mean of d_(1),d_(2),..... d_(n) is 5040 sec theta the value of n is __________. |
|
Answer» |
|