InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2651. |
Two dice are rolled. The probability that the maximum of the two numbers is greater than 4 is |
|
Answer» `8//9` |
|
| 2652. |
If |w|=2, then the set of points x+iy=w-(1)/(w) lie on |
|
Answer» Circle |
|
| 2653. |
Using binomial distribution find the mean and variance of X forthe following experiments A fair coin is tossed 100 times, and X denote the number of heads. |
|
Answer» |
|
| 2654. |
Solve the equations by matrix method:(i) x+y+z=6x+y-z=02x+y+2x=10 |
|
Answer» (II) x=2,y=-1, z=2 (III) x=1, y=2, z=5 (IV) x=2, y=-3, z=1 |
|
| 2655. |
The solution of (1+x^(2)) (dy)/(dx) + y = e^(Tan^(-1)x) is |
|
Answer» `y e^(TAN^(-1)X) = e^(Tan^(-1)x) + C` |
|
| 2657. |
If the ellipse (x^2)/4 + (y^2)/1 = 1 meets the ellipse (x^2)/1 + (y^2)/(a^2)= 1 in four distinct points and a = b^(2) - 10 b + 25, then the number of integral values of b are |
|
Answer» 3 hence `b^(2) - 10B + 25 > 1` `(b - 4)(b - 6) > 0` `b > 6 UU b < 4`. |
|
| 2658. |
A group of 123 workers went to a canteen for cool drinks, ice - cream and tea, 42 workers took ice - cream , 36 tea and 30 cool drinks , 15 workers purchased ice cream and tea, 10 ice cream and cool drinks, 4 cool drinks and tea but not ice cream, 11 took iice cream and tea but not cool drinks. Number of workers that did not purchase anything is |
|
Answer» 54 |
|
| 2659. |
Let the relation R be defined in N by aRb , if 2a + 3b = 30 . Then , R = ............. |
|
Answer» |
|
| 2660. |
An equation relating to stability of an aeroplane is (dv)/(dt)=gcosalpha-kv, where v is the velocity and g, k,alpha are constantts. If v=0. at t=0, velocity is |
|
Answer» `(gcosalpha)/(K)(1-e^(-KT))` |
|
| 2661. |
int cos x cos 2x cos 3x dx= |
|
Answer» |
|
| 2662. |
If y = sqrt(ax) + (a ^(2))/(sqrt(ax))then y _(1) , y _(2) at x =a are |
|
Answer» a |
|
| 2663. |
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (-2,4,7) and (3,-5,8). |
|
Answer» `3:2` |
|
| 2664. |
If vec(PQ)=3hati+2hatj-hatk and the co-ordinates of P is (1, -1, 2) then find the co-ordinates of Q. |
|
Answer» |
|
| 2665. |
Let a = e^("i" (2pi)/(13))then the quadratic equation whose rootsare alpha=a+a^(3) +a^(4)+a^(-4) +a^(-3) +a^(-1), beta =a^(2)+a^(5)+a^(6) +a^(-6)+a^(-5) +a^(-2) is given by |
|
Answer» `X^(2)-x-3=0` |
|
| 2666. |
If A and B are non- singular square matrix of same order 3xx3, then which of the following options is correct? |
|
Answer» `|ADJ(AB)|=|A||B|` |
|
| 2667. |
If a,b are positive quantitis and if a_(1)=(a+b)/(2), b_(1)=sqrt(a_(1)b) , a_(2)=(a_(1)+b_(1))/(2), b_(2)=sqrt(a_(2)b_(1)) and so on then |
|
Answer» `a_(oo)=SQRT(B^(2)-a^(2))/(COS^(-1)(a/b))` |
|
| 2668. |
If 'f(x)= {[Kx+1,xle5],[3x-5,x>5]:}' is continuous at x=5 then value of k is : |
| Answer» Answer :A | |
| 2669. |
If ax^2+2hxy+by^2+2gx+2fy+c=0 represents a pair of lines , prove that the area of the triangle formed by their bisectors and axis of x is sqrt((a-b)^2+4h^2)/(|2h|).|(ca-g^2)/(ab-h^2)| |
|
Answer» |
|
| 2670. |
Calculate the moment of inertia about the y-axis of the figure bounded by the parabola y^(2)= 4ax and the straight line x=a. |
|
Answer» |
|
| 2671. |
Method of integration by parts : inte^(2x) (1+sin 2x)/(1+cos 2x)dx=..... |
|
Answer» `e^(2X)TANX+c` |
|
| 2672. |
Let S be the set of all possible values of parameter 'a' for which the points of intersection of the parabolas y^(2)=3axandy=1/2(x^(2)+ax+5) are concyclic. Then S contains the interval(s) |
|
Answer» `(-OO,-2)` |
|
| 2673. |
If I_(n) = int_(0)^(pi//2) tan^(n) xdx, then I_2 + I_4, I_3+I_5,I_4 + I_6,…., are in |
|
Answer» ARITHMETIC progression |
|
| 2674. |
Events A,B,C are mutually exclusive events such that P(A)=(3x+1)/(3), P(B)=(1-x)/(4) and P(C )=(1-2x)/(2) The set of possible values of x are in the interval |
|
Answer» `[(1)/(2),(2)/(3)]` |
|
| 2675. |
Equation of the hyperbola with foci (+-2 ,0) and eccentricity 3/2 is |
|
Answer» `x^2/9-y^(2)/4=-1` |
|
| 2676. |
inte^x(cosx- sinx)dx= |
|
Answer» `-e^xcos+C` |
|
| 2678. |
Integrate the following functions 1/sqrt(x^2+2x+2) |
|
Answer» SOLUTION :`x^2+2x+2 = (x+1)^2+1` THEREFORE` int1/sqrt(x^2+2x+2) dx` =`INT 1/sqrt((x+1)^2+1) dx` =`LOG|(x+1) + sqrt((x+1)^2+1)|+c` =`log |x+1+sqrt(x^2+2x+2)|+c` |
|
| 2679. |
If the three function f(x),g(x) and h(x) are such that h(x)=f(x)g(x) and f'(a)g'(x)=c, where c is a constant, then : (f''(x))/(f(x))+(g''(x))/(g(x))+(2c)/(f(x)f(x)) is equal to : |
|
Answer» `(H(X))/( h(x)) ` |
|
| 2680. |
Distance of the point (alpha,beta,gamma) from Y- axis is …........ |
|
Answer» `BETA` |
|
| 2681. |
If sin theta= sin alpha, then |
|
Answer» `(THETA + ALPHA)/(2)` is any multiple of `(pi)/(2)` and `(theta - alpha)/(2)` is any ODD multiple of `pi` |
|
| 2682. |
Find an approximate value of the following correctedto 4 decimal places. root(7)(199) |
|
Answer» |
|
| 2683. |
If x lt - 1" then " int (1)/(sqrt(x^(2) + 2x + 1))dx = |
|
Answer» log [x + 1] + C |
|
| 2684. |
Find the area of the region {(x,y)//x^(2)-x-1 le y le -1} |
|
Answer» |
|
| 2685. |
Prove that the vectors 2hati-hatj+hatk, hati-3hatj-5hatk, 3hati-4hatj-4hatk are the sides of a right angled triangle. |
Answer» Solution :Let A,B and C be the points whose POSITION vectors are `2hati-hatj-hatk, hati-3hatj-5hatk` and `3hati-4hatj-4hatk` respectively.  Then `vec(AB) = (hati-3hatj-5hatk)-(2hati-hatj+hatk) = -hati-2hatj-6hatk` `vec(BC) = (3hati-4hatj-4hatk)-(hati-3hatj+5hatk) =2hati-hatj+hatk`. `vec(CA) = (2hati-hatj+hatk)-(3hati-4hatj-4hatk) = -hati+3hatj+5hatk` Then AB = `|vec(AB)| = sqrt(1+4+36) = sqrt(41)` BC = `sqrt(4+1+1) = sqrt6` CA = `sqrt(1+9+25) = sqrt(35)`. Now `BC^2+CA^2 = AB^2` So `triangle ABC` is a right ANGLED triangle where `ANGLEABC = 90^@` (Proved). |
|
| 2686. |
If (costheta_(1))/(costheta_(2)) +(sintheta_(1))/(sintheta_(2)) +(costheta_(0))/(costheta_(2))+(sintheta_(0))/(sintheta_(2)) =1, where theta_(1) and theta_(0) do not differ by an odd multiple of pi, then the value of |(costheta_(1)costheta_(0))/(cos^(2)theta_(2)) +(sintheta_(1)sintheta_(0))/(sin^(2)theta_(2))| is ____________. |
|
Answer» |
|
| 2687. |
The next day, on your way back from Parthenon, you see an owl injured under a large, old tree. You decide to save the owl and fix its wing, so you take it along with you. Later you get to know that owl needs to reach IIT Guwahati, India as soon as possible. Realizing how dangerous it could be for the owl to travel to India, you decide to help the owl reach its destination. You now reach Turkey. Tired by your journey, you decide to go sightseeing in the town of Istanbul. Inside the Hagia Sophia, while you are walking, you find a key-ring which has two keys on it, with a keychain as shown below. En route outside the castle, you find out that the escape is through a channel, which has two doors one behind another. Above the first door, it is written “Alphabet starts with ‘a’ ” “Look down to up, and you’ll see something interesting that satisfies me”. So you plug one of the keys into the door. A sentence appears on it, along with a keyboard. “Alohomora”. You decode what You decode what the sentence means and type in“eszrzxzbe”. The gate opened, sucking in the key plugged in and exposing another gate, with another sentence written “Incendio”. Suddenly the owl faints due to very less oxygen and you are left to decode the code. What do you type in to open the gate? |
|
Answer» syimylsz With the NUMBER of CIRCLES in keychain =26, and given HINT that BEGINS with a, the possible coding pattern is as shown. 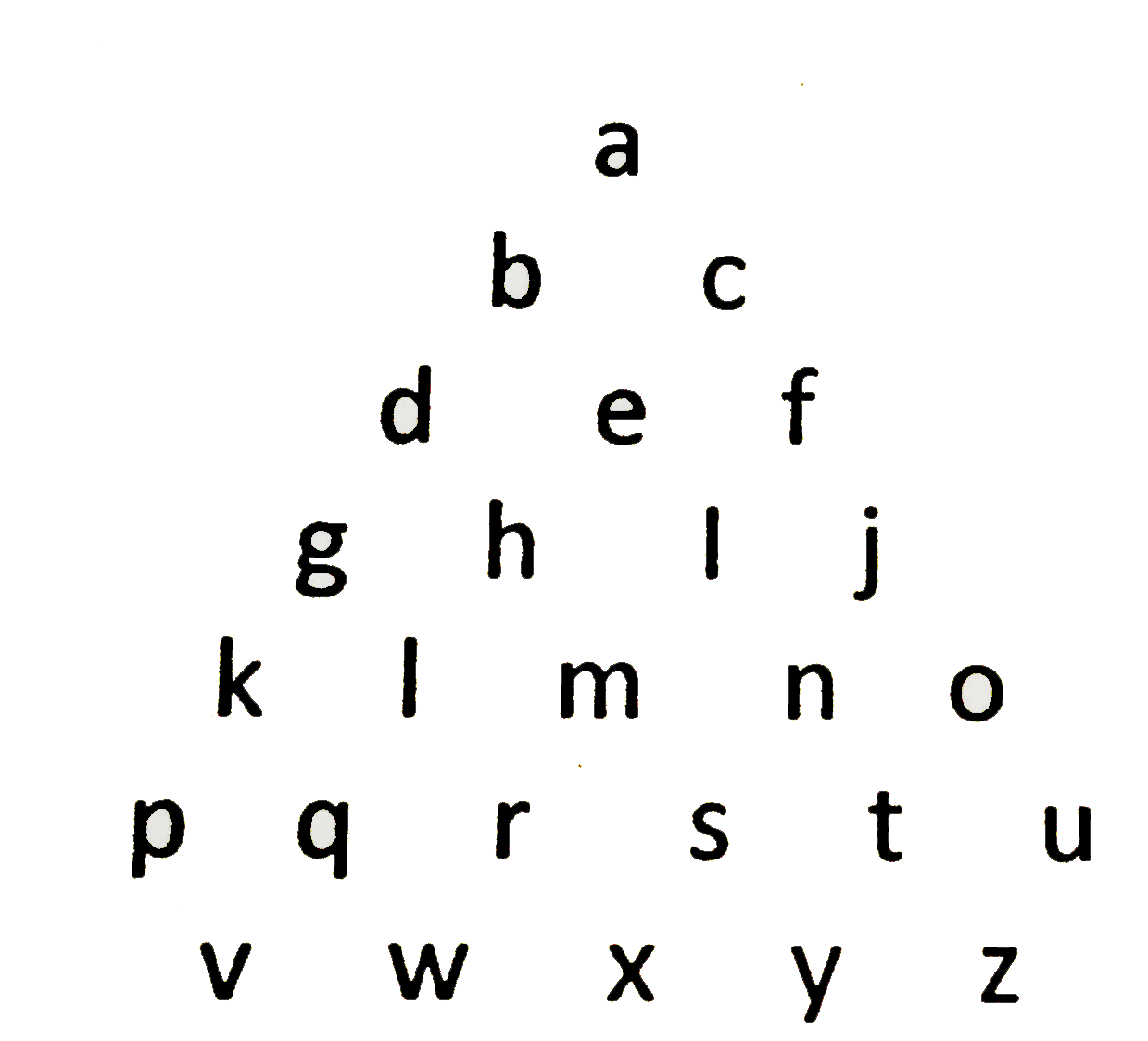 The letters are substituted by their UPPER neighbours (Alohomora = “eszrzxzbe”) So, our answer is “syimylsz”. |
|
| 2688. |
The next day, on your way back from Parthenon, you see an owl injured under a large, old tree. You decide to save the owl and fix its wing, so you take it along with you. Later you get to know that owl needs to reach IIT Guwahati, India as soon as possible. Realizing how dangerous it could be for the owl to travel to India, you decide to help the owl reach its destination. On your way to IIT Guwahati, you and your friends have to cross Aleppo. There are some safe one-way paths such that you can move only in east or south direction. Below is the map of those safe paths. You start at ‘H’ and need to reach ‘O’. The arrows show the direction you must follow on the way. Find the number of different routes that your group can take to cross the desert. |
|
Answer» <P>440 Let us work backward from ‘O’ to ‘H’. Since we can move only in right or down direction, there can be a route to the ‘O’ from only those POINTS which are to the above and left of ‘O’. From the point h7, there is only 1 route i.e. move down. Similarly, 1 route from g8. From g7, we can go to g8 or h7 and then to ‘O’hence two routes. Take any point ‘P’ and assume that ‘m’ routes are POSSIBLE from the point just below ‘P’ and ‘n’ routes are possible from the point just to the right of ‘P’. Then we can go 1 down from ‘P’and take any of the ‘m’ routes or go 1 right from ‘P’ and take any of the ‘n’ routes. Hence there are m+n routes possible from ‘P’. So, the number of routes from any point is the sum of number of routes from the point just below it and just right of it. Doing this from ‘O’ to ‘H’ we GET 75 routes as the answer. 
|
|
| 2689. |
If f(x)=x^3+x^2 +x+1thenthe coefficientofx inf(x+5)is |
|
Answer» 86 |
|
| 2690. |
Determine the range of values of theta in [0, 2pi] for which the point (cos theta, sin theta) lies inside the triangle formed by the lines x + y = 2, x – y = 1 and 6x + 2y – sqrt(10) = 0. |
|
Answer» |
|
| 2691. |
Evaluate the following integrals. int(1)/(4+5cosx)dx |
|
Answer» |
|
| 2692. |
LetS bethe setof allpointsin aplaneand letR bea relationin SdefinedbyR={(a,b):d(A,B)lt 2 units} whered(A,B)is thedistancebetweenthepointsA and B. ShowthatR isreflexive andsymmetricbutnottransitive. |
|
Answer» Solution :(i)`d(A,A)=0 lt 2. SO ,AR A. ` `(ii)A R Bimplies d(A,B)LT2` `impliesd(B,A)lt 2[:' d(B,A)=d(A,B)]` `implies B R A. ` (iii)considerthepoints `A(0,0),B(1.5,0)and C (3,0)` on thex- AXIS then`d(A,B)1.5,D(B,C)=1.5 andd (A,C)=3.` thereforeA RB and BRC butA, is notrelatedto C. So, R isnot transitive . |
|
| 2693. |
A housewife wishes to mix together two kinds of food X and Y in such a way that the mixture contains atleast 10units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg of food is given below. One kg of food x costs Rs. 60 and one kg of food y costs Rs. 100. Find the least cost of the mixture which will product the diet. |
|
Answer» |
|
| 2694. |
If P(A)=x, P(B)=y and P(AnnB)=z. Find P(A^(c )nnB^(c )). |
|
Answer» |
|
| 2695. |
Solve the equation 3x^3-7x^2-7x+3=0given that product of two of its roots is equal to 1. |
|
Answer» |
|
| 2696. |
The solution of (cosec x log y ) dy + (x^2y)dx=0 is |
|
Answer» `(log y)/2 + (2-X^2) cos x + 2 sin x =C ` |
|
| 2697. |
If (x, y, z) ne (0, 0, 0) " and " (hat(i)+hat(j)+3hat(k))y+(-4hat(i)+5hat(j))z=a(xhat(i)+yhat(j)+zhat(k)), then the value of a is - |
|
Answer» 1 |
|
| 2699. |
If vec(a).hati=4 then (vec(a)xx hatj).(2hatj-3hatk)= ……….. |
|
Answer» `-12` |
|
| 2700. |
Consider a ............. |
|
Answer» PACKING FRACTION `p=pi/6=11/21` |
|