InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 26651. |
If int_(0)^(10)f(x)dx=5, then sum_(K=1)^(10) int_(0)^(1) f(K-1+x)dx is equal to |
|
Answer» 50 |
|
| 26653. |
Show that the points A(1,-2,-8),B(5,0,-2)andC(11,3,7) are collinear , and find the ratio in which B divides AC. |
|
Answer» |
|
| 26654. |
Integrate the following functions x^2e^x |
|
Answer» Solution :`int X^2 e^x DX = x^2 e^x- int 2x e^x dx` =`x^2e^x-2 intx e^x dx` =`x^2 e^x-2[x e^x- int 1XX e^x dx]` =`x^2 e^x-2xe^x + 2 inte^x dx` =`x^2 e^x-2xe^x + 2e^x+c` =`(x^2-2x+2)e^x+c` |
|
| 26655. |
Which of the following statement is true Statement - I 2lt 1/(1!)+1/(2!)+1/(3!)+1/(4!)+ .....oo lt 3 Statement - II 1/2lt 1/(1!)+1/(2!)+1/(3!)+1/(4!)+ .....oo lt 1 |
|
Answer» only I |
|
| 26656. |
As shown in the (x,y,z) coordinate space below, the cube with vertices L through S has edges that are2 coordinate units long. The coordinates ofQ are (0,0,0) and S is on the positive x-axis . What are the coordinatesof O ? |
|
Answer» (2,0,2) |
|
| 26657. |
All the numbers that can be formed using 1, 2, 3, 4, 5 are arranged in the decreasing order. Rank of 35241 is |
|
Answer» 51 |
|
| 26658. |
If (""^(n)C_(r)+3""^(n)C_(r+1)+3""^(n)C_(r+2)+""^(n)C_(r)+3)/(""^(n)C_(r)+4""^(n)C_(r+1)+6""^(n)C_(r+2)+4""^(n)C_(r+2)+4""^(n)C_(r+3)+""^(n)C_(r)+4)=(r+k)/(n+k) ,then the value of k equals |
|
Answer» 1 |
|
| 26659. |
Evaluate lim_(n to oo) (2^(k) +4^k +6^k + ….. + (2n)^(k))/(n^(k+1)) by using the method of finding definite integral as the limit of a sum. |
|
Answer» |
|
| 26660. |
A factory makes tennis rackets and cricket bats. A tennis rackets takes 1.5 hour of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hour of machine time and 1 hour of cratman's time. In a daythe factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. (i) What number of rackets and bats must be made if the factory is to work at full capacity? (ii) If profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the maximum profit of the factory when it works at full capacity. |
|
Answer» Solution :Let `x` tennis rackets and `y` cricket bats be made in a day. Now, maximise `z=20x+10y` and constraints `XGE0` `yge0` `1.5x+3yle42` `impliesx+2yle28` `3x+yle24` Now, draw the graph of the straight lines `x=0, y=0, x+2y=28` and `3x+y=24`.  Find the FEASIBLE region from the costraints `xge0, yge0, x+2yle28` and `3x+yle24` and shade this feasible region. The vertices of this shaded region are `A(8,0), B(4,12), C(0,14)` and `O(0,0)`. We fnd the value of `Z` at these vertices. 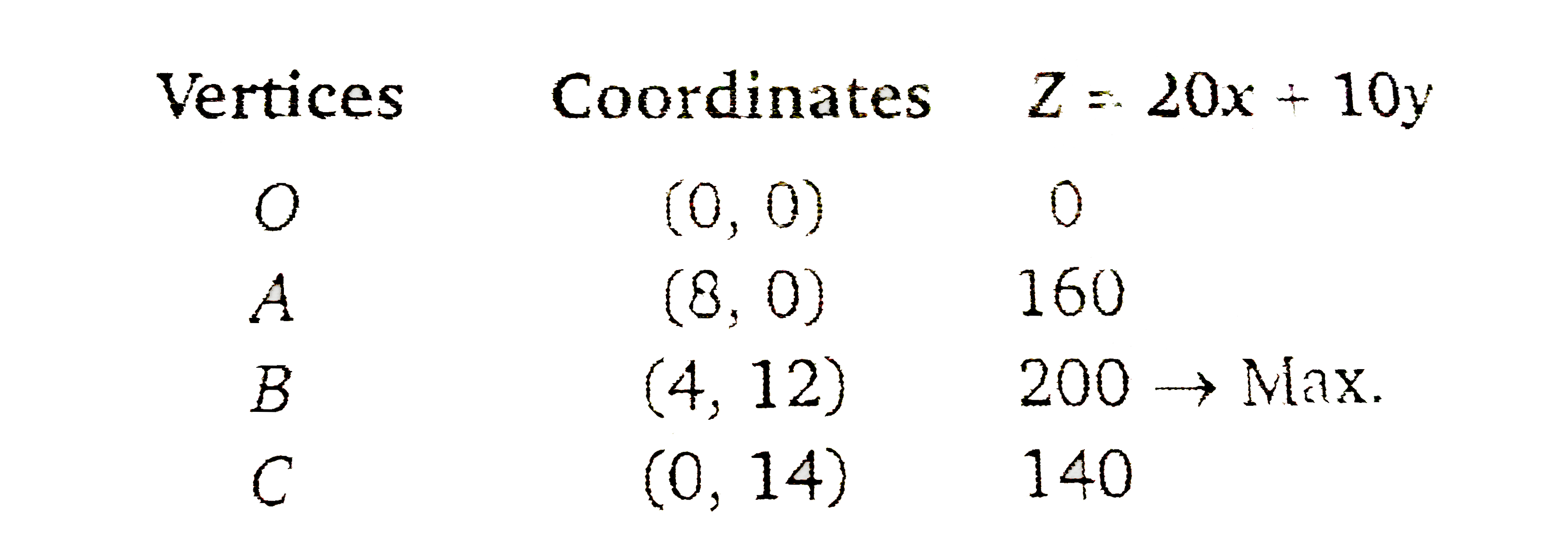 Therefore the maixmum PROFIT in RS. 200 when4 tennis racket and 12 cricket bats are made in one day. |
|
| 26661. |
If P(A)=(6)/(11), P(B)=(5)/(11) and P(A cup B)=(7)/(11),find P(A cap B) |
| Answer» | |
| 26662. |
Three normals are drawn (k,0) to the parabola y(2)=8x one of the normal is the axis and the remaining two normals are perependicular to each other, then find the value of k. |
|
Answer» |
|
| 26663. |
The probability of a gun man hitting a target is 1/3, he fires ten shots, the random variable X is the number of hits. Find the mean and variance of X. |
|
Answer» |
|
| 26664. |
Let veca+i+2j+j, vecb=i-j+k, vecv=i+h-k. A vector in the plane of veca and vecb has projection 1/sqrt3" on "vecc. Then, one such vector is |
|
Answer» 4i+j-4k |
|
| 26665. |
Let E and F events with P(E) = (3)/(5), P(F) = (3)/(10) and P(Ecap F) = (1)/(5)*Are E and F independent ? |
|
Answer» |
|
| 26666. |
Find the number of possible common tangents that exist for the following pairs of circles. x^(2) + y^(2) + 4x - 6y - 3 = 0 x^(2) + y^(2) + 4x - 2y + 4 = 0. |
|
Answer» |
|
| 26667. |
Prove the following : 4/pi lt int_(pi/4)^(pi/3) (tanx)/(x) lt (3sqrt(3))/(pi) |
|
Answer» |
|
| 26668. |
Use differential to approximate sqrt(36.6). |
|
Answer» |
|
| 26669. |
If theta is a variable parameter, then the locus represented by x=3 (cot theta - tan theta) is- |
|
Answer» an ELLIPSE |
|
| 26670. |
Let A = {(x,y) : x^(2) + y^(2) = 36} and B={(x,y) : x^(2) + 9y^(2) = 100}, Then |
|
Answer» `A cap B` is a singleton |
|
| 26671. |
The value of sum_(j=1)^(20)sum_(i=1)^(20)tan^(-1)((i)/(j)) is : |
|
Answer» `200 PI` `tan^(-1)((i)/(j))+tan^(-1)((j)/(i)) =(pi)/2`. |
|
| 26672. |
Integrate the functions 1/(cos(x+a)cos(x+b)) |
|
Answer» |
|
| 26673. |
Prove that sum_(r=0)^(2n) r.(""^(2n)C_(r))^(2)= 2.""^(4n-1)C_(2n-1). |
|
Answer» SOLUTION :`S=UNDERSET(r=0)OVERSET(2N)sumr.(.^(2n)C_(r))^(2)` `= underset(r=0)overset(2n)sum(r..^(2n)C_(r))(.^(2n)C_(r))` `= underset(r=0)overset(2n)sum(2n)^(2n-1)C_(r-1)..^(2n)C_(2n-r)` `= 2n`(Coefficient of `x^(2n-1)` in the expansion of `(1+x)^(2n-1)(1+x)^(2n))` `= 2n`(coefficient of `x^(2n-1)` in the expansion of `(1+x)^(4n-1)`) `= 2n xx .^(4n-1)C_(2n-1)` |
|
| 26674. |
Let A={1,2,3} and Let R={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)}. then ,R is |
|
Answer» REFLEXIVE and SYMMETRIC but TRANSITIVE |
|
| 26675. |
A black and red dice are rolled. Find the conditional probability of obtaining a sum8, given that the red die resulted in a number less than 4 |
|
Answer» Solution :If the event that "the red DIE is resulted in a number less than 4" is given then the ELEMENTARY cases under CONSIDERATION are REDUCED to therefore Required PROBABILITY = 2/18=1/9 |
|
| 26676. |
Integrate the functions in exercise. (x-1)/(sqrt(x^(2)-1))dx |
|
Answer» |
|
| 26677. |
Locus of midpoint of chord of circle x^(2)+y^(2)=1 which subtend right angle at (2,-1) is |
|
Answer» `X^(2)+y^(2)-2x+y-2=0` 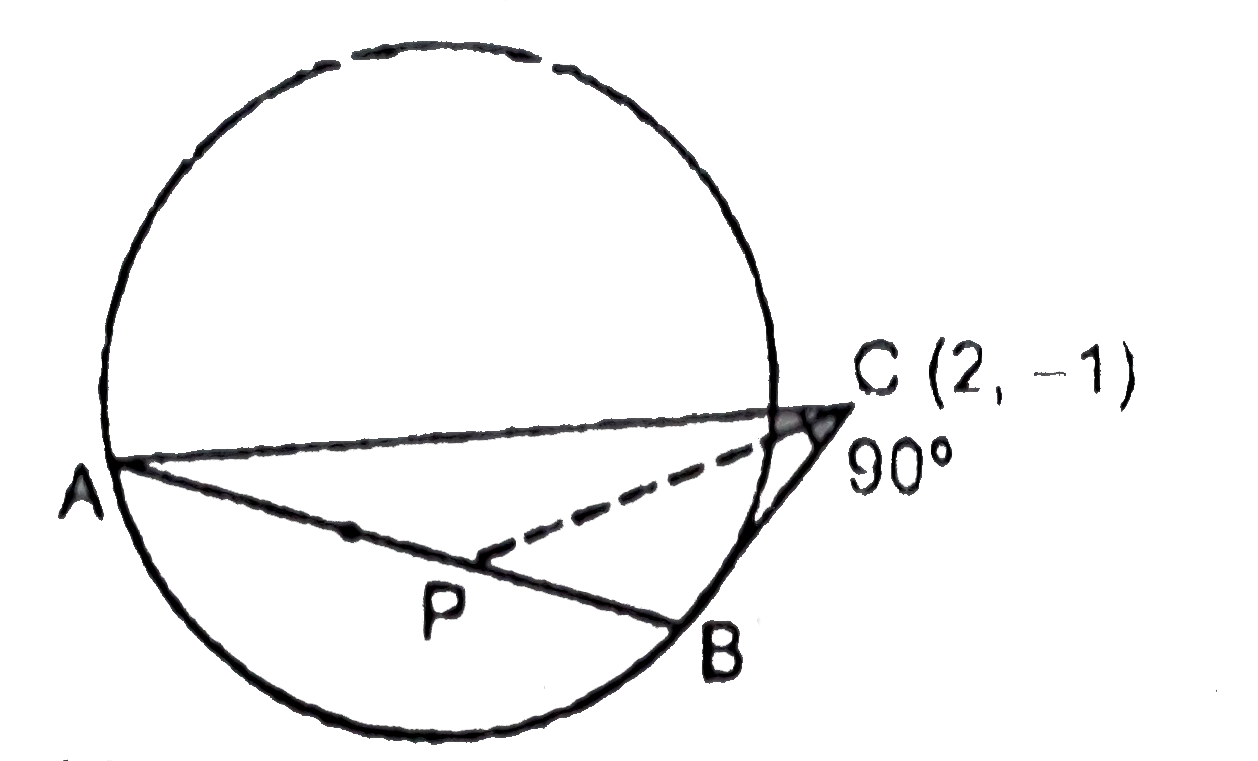 `AP=PC` `AP^(2)=PC^(2)` `AP^(2)=(H-2)^(2)+(k+1)^(2)` `(1)^(2)-(h^(2)+k^(2))=h^(2)+k^(2)-4h+2k+5` `implies2x^(2)+2Y^(2)-4x+2y+4=0` `x^(2)+y^(2)-2x+y+2=0` |
|
| 26678. |
If the line 3x-2y + 6=0 meets X-axis and Y-axis respectively at A and B, then the equalion of the circle with radius AB and centre at A. is |
|
Answer» `X^(2)+y^(2)+4x+9=0` |
|
| 26679. |
Let L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b in R, which is the farthest from the point (2, 2). If L is concurrent with the lines x-2y+1=0 and 3x-4y+ lambda=0, then the value of lambda is |
|
Answer» 2 |
|
| 26680. |
There are 8 buses running from Kota to Jaipur and 10 buses running from Jaipur to Delhi. In how many ways a person can travel from Kota to Delhi via Jaipur by bus? |
|
Answer» |
|
| 26681. |
Column-I |
|
Answer» |
|
| 26682. |
Construct truth tables for the following and indicate which of these are tautologiesprarrp^^q. |
Answer» SOLUTION :
|
|
| 26683. |
If [sin^(-1)x]^(2)-2[sin^(-1)x]+1le0 (where, [.] represents the greatest integral part of x), then |
|
Answer» `x in [sin 1, sin 2]UU[-1, 0]` |
|
| 26684. |
Find the area of the Delta le formed by the straight line 2x+y=2 and the coordinate axes using integration. |
|
Answer» |
|
| 26685. |
It is given that at x = 1, the function x^(4) – 62x^(2) + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a. |
|
Answer» |
|
| 26686. |
Evaluate int _(-3//2) ^(2) f (x)dx, where f (x) is given by f _(x) = max _(-3//2le t le x) (|t -1| -|t|+ t+1) |
|
Answer» |
|
| 26687. |
Find the area of the ellipse (x^(2))/(a^(2))+ (y^(2))/(b^(2))=1by the method of integration. |
|
Answer» |
|
| 26688. |
If A= [(0,1),(1,0)], then A^(2) equal to______ |
|
Answer» 1)`[(0,1),(0,1)]` |
|
| 26690. |
Show that area of the parallelogram whose diagonals are given by vec(a) and vec(b) is (1)/(2).|bar(a)xx bar(b)|. Also, find the area of the parallelogram, whose diagonals are 2 bar(i)-bar(j)+bar(k) and bar(i)+3bar(j)-bar(k). |
|
Answer» |
|
| 26691. |
Evaluate the following integrals. int(1)/(x^(2)+x+1)dx |
|
Answer» |
|
| 26692. |
Let the sides of a parallelogram be U=a, U=b,V=a' and V=b', where U=lx+my+n, V=l'x+m'y+n'. Show that the equation of the diagonal through the point of intersection of U=a, V=a' and U=b, V=b' " is given by " |{:(U,V,1),(a,a',1),(b,b',1):}| =0. |
Answer» Solution :Parallelogram is formed by lines U=a, U=b, V=a' and V=b', where U=lx+my+n, V=l'x+m'y+n'  Let the required diagonal be AC. SINCE ONE end A of the diagonal AC passes through the point of intersection of lines U-a=0 and V-a'=0, its EQUATION is given by `(U-a)+lambda(V-a')=0 "" (1)` But the other end C of the same diagonal passes through the point of intersection of lines U-b=0 and V-b' = 0. So, its equation is given by `(U-b)+MU(V-b') = 0 "" (2)` Equation (1) and (2) represents the same straight lines. `THEREFORE 1=(lambda)/(mu) = (a+lambdaa')/(b+mub')` `rArr lambda=mu = -((a-b)/(a'-b'))` Putting the value of `lambda` in (1), we get `(U-a)-((a-b)/(a'-b'))(V-a')=0` `" or" |{:(U,V,1),(a,a',1),(b,b',1):}| =0` This is the required equation of diagonal. |
|
| 26693. |
If x^2 - 4x + 3 equal 0, then what is the value of (x - 2)^(2) ? |
|
Answer» 0 |
|
| 26694. |
If the length of the tangent from (2,5) to the circle x^(2) + y^(2) - 5x +4y + k= 0 is sqrt(37)then find k. |
|
Answer» |
|
| 26695. |
The solution of (1 + y^(2)) dx = (Tan^(-1) y -x) dy is |
|
Answer» `X E^("Tan"^(-1)y)=(Tan^(-1)y-1)e^("Tan"^(-1)y)+C` |
|
| 26697. |
Solve the following inequation . (xx) log_(5x+4)x^2lelog_(5x+4)(2x+3) |
|
Answer» |
|
| 26698. |
Integrate the function x e^(-x) |
| Answer» | |
| 26699. |
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area? |
|
Answer» |
|
| 26700. |
int_0^4sqrt(x^2+9) |
|
Answer» SOLUTION :`int_0^4sqrt(x^2+9)` `[x/2(SQRT(x^2+9)+9/2In(x+sqrtx^2+9)]_0^4` 10+(9/2)(In9-IN3)=10+(9/2)In3` |
|