Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

4551.

A and B are two tanks, such that capacity of A is 3 times that of B. Both tanks are completely filled and their inlets are closed. Now water is released from the tanks. The rate of flow of water from each tank is proportional to the water in the tank at that instant. If after 1 hours, the water in time A is 2 times the water in tank B. Of both tanks have same quantity of water after time(log_(2m)(m)). then find(1/m).

Answer»


ANSWER :3
Discussion
4552.

A card is drawn at random from a pack, the probability that it may be either king or queen is

Answer»

`(11)/(13)`
`(1)/(13)`
`(1)/(26)`
`(2)/(13)`

Answer :D
Discussion
4553.

Integrate the following intcosec7xdx

Answer»

Solution :`intcosec7xdx`
[PUT 7x=t then DX=(1/7)DT]
`intcosectcdot(1/7)dt`
`(1/7)IOG abs(cosec7x-cot7x)+C`
Discussion
4554.

Equation of normal to y^(2) = 4x at the point whose ordinate is 4 is

Answer»

X +2y-12 = 0
x+ 2y-8 = 0
2X + y-12 =0
2x+y-8 = 0

ANSWER :C
Discussion
4555.

A :cos 20^(@) + cos 100^(@) + cos 140^(@) =0 . R :cos theta + cos (120^(@) - theta ) + cos (120^(@) + theta ) =0

Answer»

A is true , R is true and R is CORRECT EXPLANATION of A
A is true , R is trueand R is not correct explanation of A
A is true , R is false
A is false , R is true

ANSWER :A
Discussion
4556.

int 2^(x) .sin3x dx =

Answer»

`(2^(X))/((log 2)^(2) + 9)` [ (log 2 ).sin3 x - 3 cos 3x ] + c
`(2^(x))/((log 2)^(2) + 9)` [ (log 2 ).sin3 x + 3 cos 3x ] + c
`(2^(x))/((log 2)^(2) + 9)` [3 SIN 3 x - (log2). cos 3x ] + c
`(2^(x))/((log 2)^(2) + 9)` [3 sin 3 x + (log2). cos 3x ] + c

ANSWER :A
Discussion
4557.

Find the coordinates of the vertex and focus and the equations of the directrix and axis of the parabolas (i) y^(2) = 16 x

Answer»


ANSWER :EQUATION of AXIS : `y = 0`
Discussion
4558.

Find the coordinates of the vertex and focus and the equations of the directrix and axis of the parabolas (iii) 3x^(2) -9x+ 5y - 2=0

Answer»


ANSWER :EQUATION of the AXIS `: x-h=0 RARR 2x-3=0`
Discussion
4559.

Find the coordinates of the vertex and focus and the equations of the directrix and axis of the parabolas (ii) x^(2) = -4y

Answer»


ANSWER :The EQUATION of AXIS : `X = 0`
Discussion
4560.

int_(0)^(x)(2^(t))/(2^([t]))dt, where [.] denotes the greatest integer function, and x epsilonR^(+) is equal to

Answer»

`1/(1n2)([x]+2^({x})-1)`
`1/(1n2)([x]+2^({x}))`
`1/(1n2)([x]-2^({x}))`
`1/(1n2)([x]+2^({x})+1)`

Solution :Let `nlexltn+1`, where `N epsilonI`
`I=int_(0)^(x)(2^(t))/(2^([t]))DT=int_(0)^(n)2^({t})dt+int_(n)^(x)2^({t})dt`
`=n int_(0)^(1)2^({t})dt+int_(n)^(x)2^({t})dt`
`=n int_(0)^(1)2^(t)dt+int_(n)^(x)2^(t-n)dt`
`=n(2^(t))/(In2)|_(0)^(1)+1/(2^(n)) (2^(t))/(In2)|_(n)^(x)`
`=n/(In2)(2-1)+1/(2^(n)In2)(2^(x)-2^(n))`
`=n/(In2)+1/(In2)(2^(x-n)-1)`
`=([x]+2^({x})-1)/(In2)`
Discussion
4561.

Find the vertex, focus, equation of directrix and axis, of parabolas y^(2) - x + 4y + 5 = 0

Answer»


ANSWER :`y-k = 0 RARR y+2 = 0`
Discussion
4562.

A cyclist moves uniformaly on a horizontal circular track of radius 100 m . If the cofficient of friction is 0.1. At which of the following speed (s) can he travel without slipping

Answer»

5 m/s
9 m/s
14 m/s
none of these

Answer :A::B
Discussion
4563.

The solution of (dy)/(dx) + (y^(2) + y +1)/(x^(2) + x + 1) = 0is

Answer»

`TAN^(-1) (2X + 1) + Tan^(-1) (2y + 1) = c`
`Tan.^(-1) (2x + 1)/(SQRT3) + Tan.^(-1) (2y + 1)/(sqrt3) = c`
`Tan.^(-1) (2x)/(sqrt3) + Tan.^(-1) (2y)/(sqrt3) = c`
`Tan.^(-1) (2x -1)/(sqrt3) + Tan.^(-1) (2y -1)/(sqrt3) = c`

ANSWER :B
Discussion
4564.

Statement-I: The number of integral values of K for which the equation (x^(2))/(3K-2) +(y^(2))/(K-10)=1 represents a hyperbola is 10. Statement-II : The above equation represents a rectangular hyperbola for K =3. Which of above statements is true

Answer»

only I
only II
both I and II
neither I nor II

Answer :B
Discussion
4565.

The maximum number of points of intersection of 4 circles and 4 straight lines is

Answer»

25
50
56
72

Answer :B
Discussion
4566.

The system of homogenous equations (a-1)x+(a+2)y+az=0 (a+1)x+ay+(a+2)z=0 ax+(a+1)y+(a-1)z=0 has a non trivial solution if a equals

Answer»

`1/2`
`-1/2`
`2`
`-1`

ANSWER :B
Discussion
4567.

If a relation R ..............

Answer»


SOLUTION :We have `R={(X, y) : x^(2)-4xy+3y^(2)=0, x, y in N}`
Let `x in N, x^(2)-4.x.x+3x^(2)=0`
`:. (x, x) in R :. R` is reflexive
we have `(3)^(2)-4(3)(1)+3(1)^(2)=9-12+3=0`
or `(3, 1) in R`
Also `1^(2)-4(1)(3)+3(3)^(2)=1-12+27 NE 0`
`:. (1, 3) in R, :. R` is not symmetric
again `(9, 3) in R` because
`9^(2)-4(9)(3)+3(3)^(2)=108-108=0`
and `(3, 1) in R` because
`(3)^(2)-4(3)(1)+3(1)^(2)=12-12=0`
and `(9, 1) in R` if `9^(2)-4(9)(1)+3(1)^(2)=0`
if `84-36=0` which is not possible
`:. (9, 3), (3, 1) in R` and `(9, 1) in R :. R` is not transitive
`:.` Relation R is reflexive but NEITHER symmetric nor transitive.
Discussion
4568.

evaluate| [1,x,y],[1,x+y,y],[1,x,x+y] |

Answer»

SOLUTION :GIVEN DETERMINANT `|[1,X,y,],[0,y,0],[0,0,x]|` (by `R_2 rarr R_2-R_1` and `R_3rarrR_3-R_1`)
`=1xxyxx x=xy`
Discussion
4569.

A variable plane passes through a fixed point (1,-2,3) and meets the coordinate axes at point A, B, C then the point of intersection of the planes through A, B, C parallel to the coordinate planes lies on

Answer»

`XY-(1)/(2)yz+(1)/(3)zx=6`
`yz-2zx+3xy=xyz`
`xy-2yz+3zx=3xyz`
`xy-(1)/(2)yz-(1)/(3)zx=6`

Answer :B
Discussion
4570.

If z_(1), z_(2) and z_(3) are the vertices of a triangle in the argand plane such that |z_(1)-z_(2)|=|z_(1)-z_(3)|, then |arg((2z_(1)-z_(2)-z_(3))/(z_(3)-z_(2)))| is

Answer»

`(PI)/(3)`
0
`(pi)/(2)`
`(pi)/(6)`

Answer :C
Discussion
4571.

IfP_(r) is the coefficient ofx^® in the expansion of (1 + x)^(2) (1 + (x)/(2))^(2) (1 + (x)/(2^(2)))^(2) (1 + (x)/(2^(3)))^(2)...prove thatP_(r) = (2^(2))/((2^(r) -1))(P_(r-1) + P_(r-2) )and P_(4) = (1072)/(315) .

Answer»

Solution :LET `(1 + x)^(2) (1 + (x)/(2))^(2) (1 + (x)/(2^(2)))^(2) (1 + (x)/(2^(3)))^(2)...`
` = 1 + P_(1)x + P_(2)x^(2) + P_(3) x^(3) + P_(4) x^(4) + ...+ P_(r-1) x^(r-1) + P_(r) x^(r) +....`...(i)
Replacing x by `(x)/(2)` , we get
` (1 + (x)/(2))^(2) (1 + (x)/(2^(2)))^(2) (1 + (x)/(2^(3)))^(2)(1 + (x)/(2^(4)))^(2)...`
`=[1 + P_(1) ((x)/(2)) + P_(2) ((x)/(2))^(2) + P_(3) ((x)/(2))^(3)+ ...]`
On MULTIPLYING both sides by ` (1 + x)^(2)` , we get
`(1+x)^(2)(1 + (x)/(2))^(2) (1 + (x)/(2^(2)))^(2) (1 + (x)/(2^(3)))^(2)...`
`= (1 + x)^(2) [1 + P_(1) ((x)/(2)) + P_(2) ((x)/(2))^(2) + P_(3) ((x)/(2))^(3)+ ...]`...(ii)
From Eqs .(i) and (ii) , we get
` 1 + P_(1) x+ P_(2) x^(2) + P_(3) x^(3) + P_(4)x^(4) + ...+ P_(r-1) x^(r-1) + P_(r) x^(r) + ...`
`= (1 + x)^(2) [1 + P_(1) ((x)/(2)) + P_(2) ((x)/(2))^(2) + P_(3) ((x)/(2))^(3)+ ...]`
On equating coefficient of ` x^(r)` , we get
`P_(r) = P_(r)((1)/(2^(r))) + 2P_(r-1) ((1)/(2^(r-1))) + P_(r-2) ((1)/(2^(r-2)))`
` rArr P_(r) (1-(1)/(2^(r))) = (1)/(2^(r-2)) (P_(r-1) + P_(r-2))`
` rArr P_(r) (2^(2))/((2^(r-1))) = (P_(r-1) + P_(r-2))`
Now , ` P_(0) = 1 ,P_(1)= 2 + 1 + (1)/(2) + (1)/(2^(2)) + ...= 4`
`P_(2) = (2^(2) (P_(1) + P_(0)))/(2^(2)-1)=(20)/(3)`
` P_(3)=(2^(2) (P_(2) + P_(1)))/(2^(3)-1)=(128)/(21)`
`P_(4) = (2^(2) (P_(3) + P_(2)))/(2^(4) -1) = (4((128)/(21)+ (20)/(3)))/(15) = (1072)/(315)` .
Discussion
4572.

Compute the ^15C_12

Answer»

Solution :`""^15C_12 =((15)!)/((12)!3!)=(15*14*13)/(3*2)`
`5*7*13=455`
Discussion
4573.

Prove that : (vecaxxvecb)^2=|\veca|^2.|\vecb|^2-(veca.vecb)^2.

Answer»


ANSWER :T
Discussion
4574.

If A is in the third quadrant and tan A = (sqrt(7))/(3) then 18 - 16 sin^(2)^(A)/(2)-32 sin""(A)/(2)sin""(5A)/(2) =

Answer»

-6
11
5
10

Answer :B
Discussion
4575.

Evalute the following integrals int (3x + 1)/((x + 2)^(2))dx

Answer»


ANSWER :`3 log|x+2| +(5/(x+2)) + C `
Discussion
4576.

If the transformed equation of 6x^(2) + 5xy - 6y^(2)=0 when the axes are translated to the pont (-1,-1) is 6X^(2) + 5XY - 6Y^(2)+aX + bY+c=0 then the descending order of a,b,c is

Answer»

a,B,C
b,c,a
a,c,b
c,a,b

Answer :A
Discussion
4577.

Evaluate lim_(nrarroo)[((n^(2)+1)(n^(2)+1+3)(n^(2)+1+3+5).......2n" terms")/(n^(4n))]^(1l n)

Answer»


ANSWER :`25e^((2TAN^(-1)2-4))`
Discussion
4578.

I: The solution of (dy)/(dx) = (y^(2) - 2xy)/(x^(2) - 2xy) " is " xy (y -x) = c II: The solution ofxdy = [y + x cos^(2) ((y)/(x))] dx " is " tan. (y)/(x) = log (cx)

Answer»

only I is TRUE
only II is true
both I and II are true
NEITHER I nor II true

Answer :C
Discussion
4579.

Write a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.

Answer»

Solution :`*` Since g has vertical is asymptotes x = 3 and x = -3, then the denominatorof the rational function contains theproduct of (x-3) and (x+3) . Function g has the form
`g(x)=(H(x))/((x-3)(x+3)`
`*` For the horizontal asymptote to EXIST, the numerator h(x) of g(x) has same DEGREE as that of the denominator with a leading COEFFICIENT equal to -4. At the same time, h(x) has no REAL zeros. Hence
`f(x)=(-4x^(2)-6)/((x-3)(x+3))`
`*` Check the characteristics in the graph of g shown below.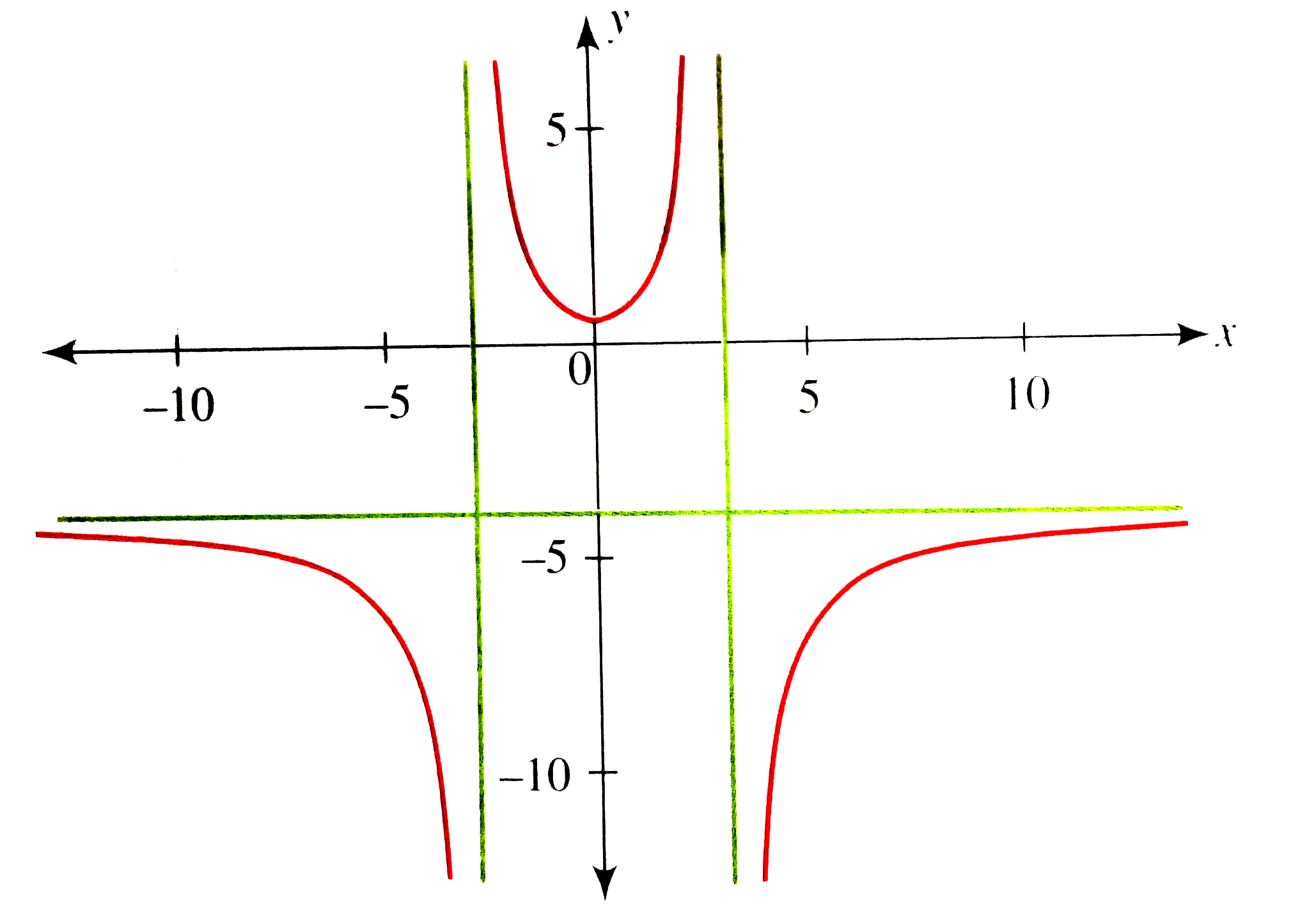
Discussion
4580.

Integration of some particular functions : int(1)/(3t^(2)+4)dt=A tan^(-1)(Bt)+c then AB=....

Answer»

`(1)/(2)`
`(1)/(4)`
1
`(1)/(3)`

Answer :B
Discussion
4581.

int sin (tan^(-1) x) dx =

Answer»

`(1)/(sqrt(x +x^(3))) +C `
`(1)/(sqrt(1- x^(2)))` + C
`sqrt(1 +x^(2)) + C`
`sqrt(1 -x^(2)) `+ C

Answer :C
Discussion
4582.

To each element of the set S= {1,2,…, 1000} a colour is assigned. Suppose that for any two elements a,b of S, if15 divides a+b then they are both assigned the same colour. What is the maximum possible number of distinct colours used?

Answer»


ANSWER :8
Discussion
4583.

Write antiderivative of tan^2x

Answer»

SOLUTION :`(x-1)/(xsqrt(x^2-1))dx=int(1/sqrt(x^2-1)-1/(xsqrt(x^2-1)))dx =In(x+(sqrt(x^2-1))-sec^(-1)x+c`
`THEREFORE` The PRIMITIVE =`In(x+sqrt(x^2-1)-sec^(-1)x`
Discussion
4584.

A: In a Delta ABC, r_1 r_2 r_3 =s^2 R: In an equilateral triangle , r:R:r_1=1:4:5

Answer»

A is TRUE, R is true and R is CORRECT explanation of A
A is true, R is true and R is not correct explanation of A
A is true, R is FALSE
A is false, R is true

Answer :D
Discussion
4585.

Find the number of ways to arrange 5 boys and 5 girl in a row such that no two of the same sex sit together

Answer»


ANSWER :`2xxlfloor5xxlfloor5`
Discussion
4586.

Compute the integrals :int _(0) ^(pi//2) " sinIn 2 x arc tan " (sin x dx )

Answer»


ANSWER :`(PI)/(2) -1`
Discussion
4587.

Method of integration by parts : int x sin x sec^(3)xdx=....

Answer»

`(1)/(2)[SEC^(2)x-tanx]+c`
`(1)/(2)[xsec^(2)x-tanx]+c`
`(1)/(2)[xsec^(2)x+tanx]+c`
`(1)/(2)[xsec^(2)x-tanx]+c`

ANSWER :B
Discussion
4588.

An inverted frustum (truncated cone) is mounted on a hemisphere of radius R. Height of the frustum is h with an opening of radius r. The vessel is filled with water. If the rate of evaportion of the liquid is proportional (constant of proportionality k gt 0) to the surface area of water in contact with air, find the time is which the vessel will be amptied.

Answer»


ANSWER :`(h+R)/(K)`
Discussion
4589.

Solve the equation 6x^4-35x^3+62x^2-35x+6=0 .

Answer»


ANSWER :`2,1/2,3,1/3`
Discussion
4590.

Area (in square units) of the region bounded by [x]^(2)=[y]^(2) for x in [1,5] ,(where [*] denotes the greatest integer function) is

Answer»

4
8
5
10

Answer :B
Discussion
4591.

Let x_(1) , x_(2) , x_(3) be the solution of tan^(-1) ((2x + 1)/(x +1 )) + tan ^(-1) ((2x - 1)/( x -1 )) = 2 tan ^(-1) ( x + 1) " where " x_(1) lt x_(2) lt x_(3) " , then " 2x_(1) + x_(2) + x_(3)^(2)is equal to

Answer»


ANSWER :1
Discussion
4592.

If f(x)=sinx+|sinx|andg(x)=f(x-pi)+f(x+2pi), then value of underset(-2pi)overset(5pi)(f)g(x)dx is

Answer»

15
7
12
28

Solution :
`:.""g(x)=F(x-pi)+f(x+2pi)`

`UNDERSET(-2pi)OVERSET(5pi)(f)g(x)dx`
`:."required area"=2[2xx7]=28`.
ALITER : `g(x)=f(x-pi)+f(x+2pi)=(-sinx+|sinx|)+(sinx|sinx|)rArrg(x)=2|sinx|`
`"So,"underset(-2pi)overset(5pi)(f)g(x)dx=28`.
Discussion
4593.

Discuss the continuity of the function f defined byf(x) = 1/(x-1) , x ne 1

Answer»

Solution :For any real number c, for `c ne 1` we have
` underset(X to c)LIM f(x) = underset(x to c) lim 1/(x -1) = 1/(c-1) `
ALSO, since for ` c ne 1 f(c)= 1/ (c-1)` we have ` underset(x to c) f(x) = f(c)` and hence f is CONTINUOUS at every point in the domain of f is a continuous function.
Discussion
4594.

The unit vectors vec(a),vec(b) and vec( c ) are not coplanar. If vec(a)xx(vec(b)xx vec( c ))=(1)/(sqrt(2))(b+c) then the angle between vec(a) and vec(b) is ………………

Answer»

`(3PI)/(4)`
`(PI)/(4)`
`(pi)/(2)`
`pi`

ANSWER :A
Discussion
4595.

The position vectors of the vertices of triangle are 3hati+4hatj+5hatk,hati+7hatk and 5hati+5hatj. The distance between ortho centre and circum centre is ………….

Answer»

`=0`
`SQRT(306)`
`2sqrt(306)`
`(3)/(2)sqrt(306)`

Answer :B
Discussion
4596.

If a,b,c,d be four consecutive coefficients in the binomial expansion of (1+x)^(n), then value of the expression (((b)/(b+c))^(2)-(ac)/((a+b)(c+d))) (where x gt 0 and n in N) is

Answer»

positive
negative
zero
depends on `n`

Solution :`(a)` `a=^(n)C_(r-1)`, `b=^(n)C_(r )`, `C=^(n)C_(r+1)`, `d=^(n)C_(r+2)`
`a+b=^(n+1)C_(r )`
`b+c=^(n+1)C_(r+1)`
`c+d=^(n+1)C_(r+2)`
`(a+b)/(a)=(n+1)/(r )`
`implies(a)/(a+b)=(r )/(n+1)`, `(b)/(b+c)=(r+1)/(n+1)`, `(c )/(c+d)=(r+2)/(n+1)`
`:. (a)/(a+b)`, `(b)/(b+c)`, `(c )/(c+d)` are in `A.P.`
`A.M. gt G. M.`
`(b)/(b+c) gt SQRT((ac)/((a+b)(c+d)))`
`implies((b)/(b+c))^(2)-(ac)/((a+b)(c+d)) gt 0`
Discussion
4597.

Evaluate the following integrals int((3e^(x)-4)e^(x))/(e^(2x)-2e^(x)+10)dx

Answer»


ANSWER :`(3)/(2)log|E^(2x)-2E^(x)+10|-(1)/(3)TAN^(-1)((e^(x)-1)/(3))+c`
Discussion
4598.

C : x^2+y^2=9, E:(x^2)/(9)+(y^2)/(4)=1,L, y=2x P is a point on the circle C, the perpendicular PQ to the major axis of the ellipse E meets the ellipse at M, then (MQ)/(PQ) is equal to :

Answer»

`(1)/(3)`
`(2)/(3)`
`(1)/(2)`
NONE of these

Answer :B
Discussion
4599.

Let a = p (hati + hatj + hatk ).b = hati + hatj - 2 hatk" and "c= 2 hati - hatj + 2 hatkbe three vecotrs . If the values of [a b c] is not more than15 and not lees than -5, then the p lies in the interval

Answer»

`( (-5)/(3) , 5/9)`
`( (-15)/(9) , 5/9)`
`(0, 5/9)`
`( (-5)/(3) , 5/9)`

ANSWER :D
Discussion
4600.

Let each side of smallest square of chess boards is one unit in length. Find the total number of rectangles (including squares) whose side parallel to side of chess board

Answer»


ANSWER :1296
Discussion