InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4651. |
Let [x] denote the largest interger not exceeding x and {x}=x-[x]. Then int_(0)^(2012) e^(cos (pi{x}))/(e^(cos (pi{x}))+e^(-cos(pi{x})))dx is equal to - |
|
Answer» SOLUTION :`I=2012 underset(0)overset(1)(int) E^(cos pi x)/(e^(cos pi x)+e^(-cos pi x))dx` using king PROPERTY `I =2012 underset(0)overset(1)(int) e^(-cos pi x)/(e^(-cos pi x)+e^(cos pi x))dx rArr 2I=2012 rArr I=1006` |
|
| 4652. |
Find the equation of perpendicular bisector of the plane of the line segment joining (1, 2, -3) and (-3, 6, 4). |
|
Answer» |
|
| 4653. |
An equation of the tangent at the point (5,2) of a circle is given by 3x -2y -11=0. If the circle passes through the origin, an equation of the circle is |
|
Answer» `x ^(2) +y ^(2) -23 x -102 y =0` |
|
| 4654. |
The solution ofsqrt(1 + x^(2)) dx + sqrt(1 + y^(2)) dy = 0 is |
|
Answer» `xsqrt(1+x^(2)) + ysqrt(1+y^(2)) + SIN h^(-1)x + sin h^(-1) y = C` |
|
| 4655. |
Find the coefficient of x^5 in (1 + x + x^2 + x^3)^5 (1+x+x^2 + x^3 + x^4)^(-5) |
|
Answer» |
|
| 4656. |
Determine the truth of falsity of the If A,B,C are sets, then either A = B or A sub B or B sub A propositions with reasons. |
| Answer» SOLUTION :If A,B,C are sets, then either `A= B or A sub B` or `B sub A`. It is false, as there is POSSIBILITY for `A!=B`. | |
| 4657. |
If lim_(x to 0) (log (3+x)-log (3-x))/x=k, the value of k is |
|
Answer» `-1/3` |
|
| 4658. |
There is 4% error in measuring the period of a simple pendulum. The approximate percentage error in length is …….. Hint : T = 2pi sqrt((l)/(g)) |
| Answer» ANSWER :B | |
| 4659. |
There are 50 tickets in a lottery in which there is a first and a second prize. What is the probability of a man drawing prize if he owns 5 tickets ? |
|
Answer» |
|
| 4660. |
Compute the area of the portion of the cylinder surface x^(2) + y^(2) = ax situated inside the sphere x^(2) + y^(2) + z^(2) = a^(2) |
|
Answer» |
|
| 4661. |
Which of the following set of quantum numbers is impossible for an electron ? |
|
Answer» `N = 1, l = 0,m_(l) = 0,m_(s) = +(1)/(2)` |
|
| 4663. |
Find the co-ordinates of the point where the line through A(3, 4, 1) and B(5, 1, 6) cross the XY- plane. |
|
Answer» |
|
| 4664. |
Prove that ""^(10)C_(2)+2xx^(10)C_(3)+^(10)C_(4)=^(12)C_(4) |
|
Answer» `2^(20) - 2^(5)` |
|
| 4665. |
If x= a cos^(3) theta, y= a sin^(3) theta, then 1 + ((dy)/(dx))^(2) is______ |
|
Answer» 1 |
|
| 4666. |
The shortest distance between the line y-x =1 and the curve x=y^2 is |
|
Answer» `( 2sqrt3)/( 8) ` |
|
| 4667. |
Integrate the following functions (x e^x)/(1+x)^2 |
|
Answer» Solution :`int (x e^x)/(1+x^2) dx` =`int e^x((x+1-1)/(1+x)^2) dx` =`int e^x (1/(1+x) - 1/(1+x)^2) dx` =`e^x/(1+x) +C`, Here F(x) = 1/(1+x) `f^.(x) = -1/(1+x)^2` |
|
| 4668. |
Find the area enclosed by circle x^(2)+y^(2)=4, parabola y=x^(2)+x+1, the curve y=[sin^(2)x/4+cos x/4] and X-axis (where,[.] is the greatest integer function. |
|
Answer» |
|
| 4669. |
For any vector vec(x), the value of (vec(x)xxhat(i))^(2)+(vec(x)xxhat(j))^(2)+(vec(x)xxhat(k))^(2) is equal to |
|
Answer» `|VEC(X)|^(2)` |
|
| 4670. |
Assertion (A): If n is a multiple of 6 and alpha, betaare the roots of x^(2) + x +1=0 then (1+alpha)^(-n)+ (1+beta)^(-n)=2 Reason (R) : The roots of x^(2) + x + 1= 0 are omega, omega^(2) and omega^(n), omega^(2n)= 2 when n=3k, k in z |
|
Answer» Both A, R are TRUE and R EXPLAIN Assertion |
|
| 4671. |
Choose the correct answer. int_0^sqrt3 dx/(1+x^2) |
|
Answer» `PI/3` |
|
| 4672. |
Evaluate the definite integral in exercise overset(2)underset(0) int (6x+3)/(x^(2)+4)dx |
|
Answer» |
|
| 4673. |
Chord joining A(theta_1)" and "B(theta_2) is reflected by the ellipse,(x^2)/(a^2)+(y^2)/(b^2)=1, at B, if AB is a focal chord and the reflected ray meets the ellipse again at C(theta_3) , then (Given theta_1,theta_2 ne (nx)/(2),n in Z) (where e equal to eccentricity of ellipse) |
|
Answer» `E=|(COS((theta_1-theta_2)/(2)))/(cos((theta_1+theta_2)/(2)))|` |
|
| 4674. |
For all real values of x, the minimum value of (1-x+x^(2))/(1+x+x^(2)) is |
| Answer» ANSWER :D | |
| 4675. |
prove that the line 2x + y = 1 is a tangent to the circle x^2+y^2+6x-4y+8=0. |
|
Answer» Solution :`x^2+y^2+6x-4y+8=0` `therefore` g = 3, F = -2, c = 8 `therefore` Centre at (-3, 2) and radius is sqrt(g^2+f^2-c) = sqrt(9+4-8) = sqrt5` Distance of the centre from the line 2X + y -1 = 0 is `abs((2(-3)+1xx2-1)/sqrt(4+1))` = `abs((-6+2-1)/sqrt5) = sqrt5` `therefore` The line touches the CIRCLE` |
|
| 4676. |
Write down negations of It is raining and it is cool. |
| Answer» SOLUTION :It is not RAINING or it is not COOL. | |
| 4677. |
The normal at P(x_(1),y_(1)) on the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2))=1 meets the coordinate axes at A and B. If O, is u b the origin and e, the eccentricity of the hyperbola, then |
|
Answer» `OA=e^(2)x_(1)` |
|
| 4678. |
Find the number of pairs of positive integers (m,n) with m le n, such that the 'least common multiple' (LCM) of m and n equals 600. |
|
Answer» |
|
| 4679. |
Let f_(i)(x)=sin(2p_(i)x) for i=1,2,3 & p_(i) in N. If is given that the fundamental periods of f_(1)(x)+f_(2)(x)+f_(3)(x), f_(1)(x)+f_(2)(x) and f_(1)(x)+f_(3)(x) are pi, (pi)/(3) respectively, then the minimum value of p_(1)+p_(2)+p_(3) is |
|
Answer» |
|
| 4680. |
Find the coordinates of the point which divides the line segment joining the points A (4,6),B (-3,1) in the ratio 2:3 internally. Find also the coordinates of the point which divides bar(AB) in the same ratio externally. |
|
Answer» Solution :The COORDINATION of the point P is ` `((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))` `(6/5,20/5)=(6/5,4)` If the point C divides `bar^AB` externally in the RATIO 2:3, then the COORDINATES of the point C is `((mx_2+nx_1)/(m-n),(my_2-ny_1)/(m-n))` `((2(-3)-3.4)/(2-3),(2.1-3.6)/(2-3))` `((-6-12)/-1,(2-18)/-1)=(18,16)`. |
|
| 4681. |
The maximum value of |{:(1,1,1),(1,1+sintheta,1),(1,1,1+costheta):}| is 1/2 |
|
Answer» |
|
| 4682. |
Evaluate the following improper integrals : (a) int_(0)^(oo)(1nx)/(1+x^(2))dx, (b) int_(0)^(oo)e^(-x^(2)x^(2m+1))dx |
|
Answer» (B) `(m!)/(2)` |
|
| 4683. |
Match the conic in List I with the statements/expressions in List II. |
|
Answer» CLEARLY distance between COMPLEX numbers '2' and `'-2'` is 4 which is less then 3. So, locus of z is a branchof the hyperbola. s. If eccentricity is `[1,oo)`, then the conic can be a parabola (if e = 1) and a hyperbola if `e in (1,oo)`. Note. SOLUTIONS of the REMAINING parts are GIVEN in their respective chapters. |
|
| 4684. |
For each the followingdifferential equaltions determine ists order degree (if exists ) (i) (dy)/(dx)+xy=cotx (ii) (d^(3)y)/(dx^(3))^(2/3)-3(d^(2)y)/(dx^(2))+5(dy)/(dx)+4=0 (iii) (d^(2)y)/(dx^(2))^(2)+(dy)/(dx)^(2)=x sin (d^(2)y)/(dx^(2)) (iv) sqrt(dy)/(dx)-4(dy)/(dx)-7x=0 (v) y(dy)/(dx)=(x)/((dy)/(dx)+(dy)/(dx))^(3) (vi) x^(2)(d^(2)y)/(dx^(2))+[1+(dy)/(dx)^(2)]^(1/2)=0 (vii) (d^(2)y)/(dx^(2))^(3)=sqrt(1+(dy)/(dx)) (viii)(d^(2)y)/(dx^(2))=xy+cos(dy)/(dx) (ix)(d^(2)y)/(dx^(2))+5(dy)/(dx)+intydx=x^(3) x=e^(xy)(dy)/(dx) |
|
Answer» (ii) 0 (IV) 0 (V) 4 (VI)0 (vii) 6 (ix) 1 (x) not exist |
|
| 4685. |
An ellipse of major and minor axes of length sqrt(3) and 1 respectively, slides along the coordinate axes and alwys remains confined in the first quadrant. The locus of the centre of the ellipse will be the arec of a circle. The length of the arc is |
|
Answer» `PI` |
|
| 4686. |
Statement-1 : sin78^(@)+sin52^(@)+sin50^(@)=4cos25^(@)cos26^(@)cos39^(@) Statement-2 : If A+B+C=pi, then. cosA+cosB+cosC=4cos.(A)/(2)cos.(B)/(2)cos.(C)/(2). |
|
Answer» Statement-1 is TRUE, statement-2 is true, statement-2 is a CORRECT EXPLANATION for statement-2 |
|
| 4687. |
vec(a)=2hati+hatj+hatk and vec(b)=hati-hatj-hatk are the adjacent sides of a parallelogram. The angle between their diagonals is ……………… |
|
Answer» `cos^(-1)((1)/(3))` |
|
| 4688. |
Which of the following statements is/are false? p : 137 is an integer or rational number q : Birds has wings or colour of sky is blue r : One of every three consecutive integer is divisible by 3 or product of every two consecutive integer is odd |
|
Answer» <P>p only |
|
| 4689. |
If |(lamda^(2)+3lamda, lamda-1, lamda+3),(lamda+1, 2-lamda,lamda-4),(lamda-3, lamda+4, 3lamda)|=plamda^(4)+qlamda^(3)+rlamda^(3)+slamda+t,then t= |
|
Answer» 22 |
|
| 4690. |
Find the mean deviation about the median for the following data 4,6,9,3,10,13,2 |
|
Answer» |
|
| 4691. |
int_(sqrt(2)-1)^(sqrt(2)+1)(x^(4)+x^(2)+2)/((x^(2)+1)^(2))dx=k, find the value of k- |
|
Answer» |
|
| 4692. |
Two numbers are selected at random (with-out replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Then E(X) is |
|
Answer» `(2)/(3)` |
|
| 4693. |
For theta in (0(pi)/(2)), "sech"^(-1) (cos theta)= |
|
Answer» `log|tan((pi)/(6)+(THETA)/(2))|` |
|
| 4694. |
The value of int_(-pi//2)^(pi//2)(x^(3)+xcosx+tan^(5)x+1)dx= |
| Answer» ANSWER :D | |
| 4696. |
A company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. Atfactory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand. |
|
Answer» `50x+40 ge 6400 Rightarrow 5x +4Y ge 640 ,.....(i)` Also, at factory l, 50 calculators of model 8 and at factory II, 20 calculators of modal 8 are made everyday Since, the company has ordered atleast 4000 calculators of model B `therefore 50x+20y ge 4000 Rightarrow 5x+2y ge 4000...(ii)` Similarly for model C, 30x+40y ge 4800 `Rightarrow 3x+4y ge 480 ...(iii)` Also,`x ge 0, y ge 0 ...(iv)["Since x and y are non negative"]` If costs 12000 and 15000 each day to operate factories I and II respectively. Corresponding LPP is Minimise Z=12000x+15000y, "subject to" `5x+6y ge 640` `5x+2y ge 480` `3x+4y ge 480` `x ge 0, y ge 0` on solving 3x+4y=480 and 5x+4y=640, we get x=80, y=60 On solving 5x+4y=640, we get x =32, y=120 Thus from the GRAPH it is clear that feasible region is unbounded and the coordinates of corner points A,B,C and D are (160,0),(80,60),(32,120) and (0,200) respectively 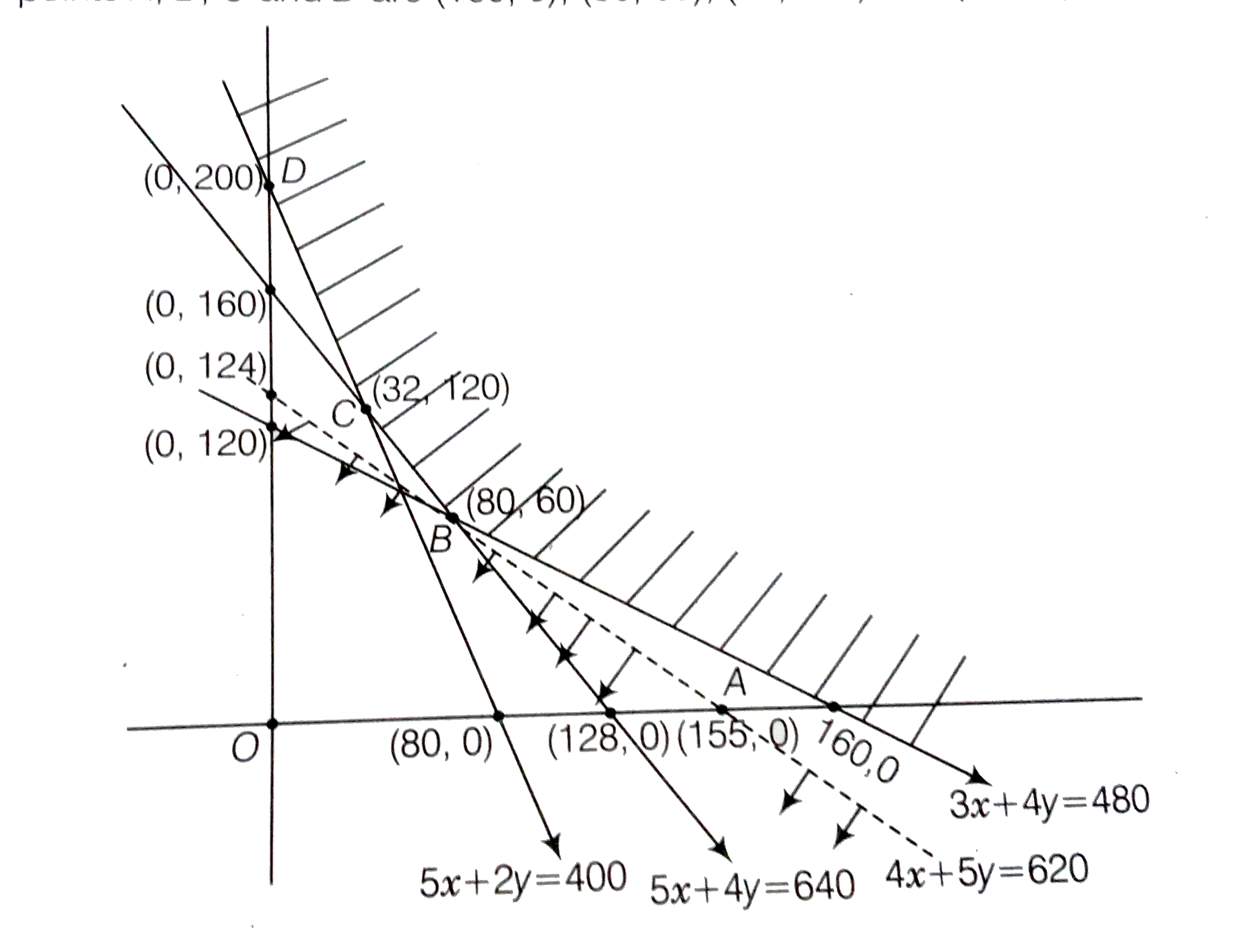  From the above table, it is clear that for given unbouded region the minimum valur of Z may or may not be 1860000. Now for deciding this, we graph, the inequality 12000x+15000y lt 1860000 `4x+5y lt 620` and check whether THERESULTING open half plane has points in common with feasible region or not. Thus, as shown in the figure it has no common points so, Z=12000x+15000y has minimum value 1860000. Som number of day factory I should be operated is 80 and number of days factory II should be operated is 60 for the minimum cost and SATISFYING the given constraints. |
|
| 4697. |
int _(-2)^(2)|x cos pi x |dx is equal to |
|
Answer» `8/pi` `= 2 { int _(0)^(1/2) | x cos pi x | dx + int _(1/2)^(3/2) | x cos pi x | dx + int _(3/2)^(2)| x cos pi x | dx }` ` = 2 [ int _(0)^(1//2) cos pi xdx + int _(1//2)^(3/2) x cospi x dx + int _(3//2)^(2) x cos pi xdx]` ` = 2 [ [ (XSIN pix)/pi + (cos pi x)/(pi^(2))]_(0)^(1//2) - [ (x sin pi x)/pi + (cos pi x)/(pi^(2))] _(1//2)^(3//2)` ` + [ (x sin pi x)/pi + (cos pix)/(pi^(2))]_(3//2)^(2)]` ` = 2 [ (1/(2pi)- 1/(pi^(2)))-((-3)/(2pi)-1/(2pi))+(1/(pi^(2))+3/(2pi)) ] ^(1//2) = 2 xx 8/(2pi) = 8/(pi)` |
|
| 4698. |
Find P(AnnB)If A and B are independent events with P(A)=1/5 and P(B)=5/8.a)6/13 b)33/40 c)1/8 d)5/8 |
|
Answer» `6/13` |
|
| 4699. |
int_(0)^((2pi)/(3)) sqrt( 1+ cos 2x )dx=……… |
|
Answer» `-sqrt6` |
|
| 4700. |
Find the equation of tangents of the circle x^(2) + y^(2)-10 = 0 at the points whose abscissae are 1. |
|
Answer» |
|