InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4751. |
Show that the function defined by f(x)= |cos x| is a continuous function. |
|
Answer» |
|
| 4752. |
When the tens digit of a three digit number abc is deleted, a two digit number ac is formed. How many numbers abc are there such that abc=9ac + 4c. |
|
Answer» |
|
| 4753. |
If a plane meets the coordinate axes at A, B, C, and DeltaABC has centroid at the point G(a//2,b//2,c//2), then the equation of the plane is |
|
Answer» `(x)/(a)+(y)/(b)+(Z)/(C )=(3)/(2)` |
|
| 4754. |
Which of the following statements is false : |
|
Answer» If |A| =0 then |adj A| =0 |
|
| 4755. |
Find the 5th term of the extension (x - 1/x)^10 |
| Answer» | |
| 4756. |
The no. of normals drawn to (y-1) ^(2) =8 ( x+3)through(4,1 ) |
|
Answer» 3 |
|
| 4757. |
Fill in the blank choosing correct answer from the brackets if theta = cos^(-1) x + sin^(-1) x-tan^(-1) x, x ge 0, then the smallest interval in whichtheta lies is ___.((pi/2,(3pi)/4),[0,pi/2),(0,pi/2]) |
| Answer» SOLUTION :`(0,pi/2]` | |
| 4758. |
State which of the following matrices is symmetric,slew symmetric, both or not either:[[0,1],[1,0]] |
| Answer» SOLUTION :SYMMETRIC | |
| 4759. |
Evaluate the following integrals inte^(2x)cosxcos3xdx |
|
Answer» |
|
| 4760. |
solve the following equation , given that they have multiple roots . 3x^4+16x^3+24x^2-16=0 |
|
Answer» |
|
| 4761. |
Find a vector of magnitude 3 and perpendicular to both the vectors barb-2bari-2barj+bark, barc=2bari+2barj+3bark. |
|
Answer» |
|
| 4762. |
Find the area of the circle x^(2) + y^(2) = 4 bounded by the lines x = 0 and x = 2 which is lying in the first quadrant. |
|
Answer» `PI` |
|
| 4763. |
A minimum value of int_(0)^(x)(te^(t^2))dt IS |
|
Answer» 0 |
|
| 4764. |
Solve the following differential equations. (i) Solve sqrt(1-x^(2)) dy + sqrt(1-y^(2))dx = 0 (ii) Solve x+y (dy)/(dx) = 0 (iii) Solve (dy)/(dx) = (2y)/(x) (iv) Solve (dy)/(dx) + x^(2) = x^(2)e^(3y) |
|
Answer» (iii) `y = CX^(2)` (iv) `1-e^(-3Y) = c e^(x^(3))` |
|
| 4765. |
int sinh^(-1) ((x)/(4)) dx = |
|
Answer» `xsinh^(-1) ((X)/(4)) - SQRT(x^(2) + 16) + C ` |
|
| 4766. |
Somehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!” Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice. Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece. A 8x8 chess board is in the shape of a torus, where the chess board is on the outer surface of the torus(as shown below). How many minimum number of Knights are required to totally dominate it? |
|
Answer» 8 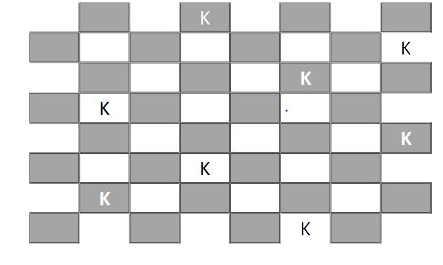
|
|
| 4767. |
Somehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!” Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice. Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece.How many ways can you arrange 4 queens such that they will dominate a 5*9 chess board? |
|
Answer» 4 |
|
| 4768. |
Somehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!” Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice. Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece. What are the minimum number of moves knights have to make on the given 8*6 chess board so that in their final position, they dominate the entire chessboard if the initial position is as given in the figure beside? |
|
Answer» 8 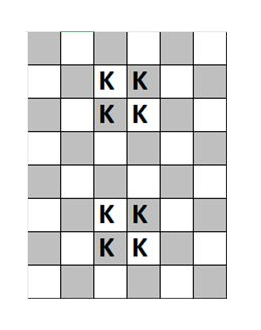
|
|
| 4769. |
If a plane meets the co-ordinate axes in A, B, C such that the centroid of the triangle ABC is the point (1,r,r^(2)), then equation of the plane is |
|
Answer» `x+ry+R^(2)z=3r^(2)` |
|
| 4771. |
If the position vectors of the vertices A, B and C are 6hat(i), 6hat(j) and hat(k) repsectively w.r.t. origin O, the volume of the tetrahedron OABC is |
|
Answer» 6 cu units `OA =6 hati =6 hati+0 hatj+0hatk` `OB=6 hatj =0hati +6 hatj +0hatk` `and OC =hatk=0hati+0hatj+hatk` Now, volume of the tetahedron `=1/6{OA OB OC ]=1/6 |{:(6,0,0),(0,6,0),(0,0,1):}|` `=1/6(6xx6xx1)=6` cu units |
|
| 4772. |
Select the correct answer:Degree of [1+(dy/(dx))^2]^(3/2)=5(d^3y/(dx^3)) |
| Answer» Answer :C | |
| 4773. |
A man 2m tall walksat a uniform speed of 4m/min away from a lamp post 6m high. Find the rate at which the length of his shadow decreases. |
|
Answer» |
|
| 4774. |
If f_(n)(x)=log log log ....log x(log is repeated n times, then int[(xf_(1)(x)f_(2)(x).....f_(n)f(x)]^(-1)dx= |
|
Answer» `f_(N+1)(x)+C` |
|
| 4775. |
Find the number of ways in which 6 red roses and 3 white roses of different sizes can be made out to form a garland so that all the white roses come together |
|
Answer» |
|
| 4776. |
Find the number of ways in which 6 red roses and 3 white roses of different sizes can be made out to form a garland so that no two white roses come together |
|
Answer» |
|
| 4777. |
At a point (x_1,y_1) on the curve x^3+y^3=3axy, show that the tangent is (x_1^2-ay_1)x+(y_1^2-ax_1)y=ax_1y_1. |
|
Answer» |
|
| 4778. |
A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (= a) subtends an angle of 60^(@) at the face of the lower and the angle of elevation of the top of the tower from A or Bis 30^(@).The height of the tower is: |
|
Answer» `2A SQRT3` |
|
| 4779. |
Which of the following sentences are propositions and which are not ? Write with reason :You must go to school everyday . |
| Answer» Solution :You must go to school EVERYDAY. It is not a STATEMENT as it is NEITHER true nor FALSE. | |
| 4780. |
What can you say about the set, A,B,if A\B=U.(where U is the universal set) |
| Answer» SOLUTION :`A-B =U IMPLIES A=U `and `B=phi` | |
| 4781. |
A woman wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitaminA and 11 units of vitamin B. Food I costs Rs. 60//kg and food of vitamin B. Food II cost Rs. 80/kg. Food I contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food II contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Find the minimum cost of the mixture. |
|
Answer» |
|
| 4782. |
Solve : x^6-6x^5+10x^4-9x^2+6x-2=0 given that (2+sqrt3) and (1+i) are roots. |
|
Answer» |
|
| 4783. |
If the point of intersection of the pair of the transverse common tangents and that of the pair of direct common tangents drawn to the circles x^(2) + y^(2) -14 x + 6 y + 33 = 0 andx^(2) + y^(2) + 30 x - 2y + 1 =0 are T and D respectively, then the centre of the circle having TD as diameter is |
|
Answer» `(39/2,(-7)/4)` |
|
| 4785. |
Let P_(1) denote the equation of a plane to which the vector (hati+hatj) is normal and which contains the line whose equation is vecr=hati+hatj+veck+lamda(hati-hatj-hatk)andP_(2) denote the equation of the plane containing the line L and a point with position vector j. Which of the following holds good? |
|
Answer» The equation of `P_(1)" is"x+y=2.` `vecr=hati+hatj+hatk+lamda(hati-hatj-hatk)`, HENCE contains the point `hati+hatj+hatk` and is normal to vector `(hati+hatj)`. Hence, equation of plane is `""(vecr-(hati+hatj+hatk))*(hati+hatj)=0` or `""x+y=2` Plane `P_(2)` contains the line `""vecr=hati+hatj=hatk+lamda(hati-hatj-hatk)` and point `hatj` Hence, equation of plane is `|{:(x-0,,y-1,,z-0),(1-0,,1-1,,1-0),(1,,-1,,-1):}|=0` or`""x+2y-z=2` If `theta` is the acute angle between `P_(1) and P_(2)`, then `""costheta= (vec(n_1)*vec(n_2))/(|vec(n_1)||vec(n_2)|)=|((hati+hatj)*(hati+2hatj-hatk))/(SQRT2*sqrt6)|` `""= (3)/(sqrt2*sqrt6)= (sqrt(3))/(2)` `""theta=cos^(-1)""(sqrt(3))/(2)= (pi)/(6)` As `L` is containec in `P_(2) rArr theta=0` |
|
| 4786. |
{:(" " Lt),(n rarroo):}1/n ((1)/(n+1) +(2)/(n+2)......+3/(4n))= |
| Answer» Answer :D | |
| 4787. |
If sum of the series overset(oo)underset(j=0)Sigma overset(oo)underset(k=0)Sigma ((1)/(5^(j)))((1)/(5^(k))) is S then 12S= |
|
Answer» |
|
| 4788. |
Integrate the following : int(2sqrtx+3/sqrtx)dx |
|
Answer» Solution :`int(2sqrtx+3/sqrtx)dx` =2`int(x)^(3/2)dx`+3`int(x)^(-1/2)dx` `2x^(3/2)/(3/2)`+`3X^(1/2)/(1/2)`+C=`(4/3)x^(3/2)`+`6X^(1/2)`+C |
|
| 4789. |
A hyperbola with foci at (0,-1), (0,3)and the vertex at the origin is |
|
Answer» `3y^2 - x^2 - 6Y = 0` |
|
| 4790. |
Find the equation of polar of the point (i) (3,-1) with resect to the cirlce 2x^(2)+2y^(2)=11 (ii) (2,3) with respect to the circle x^(2)+y^(2)+6x+8y-96=0 (iii) (4,3) with respect to the circle x^(2)+y^(2)-8x-6y-9=0 (iv) (1,2) with respect to the cirlce x^(2)+y^(2)=7 (v) (1,-2) with respect to the circle x^(2)+y^(2)-10x-10y+25=0 |
|
Answer» (III) does not EXIST (IV) `x+2y-7=0` (v) `4x+7y-30=0` |
|
| 4791. |
If x is a comples cube root of unity and A={:[(1,1,1),(1,x,x^(2)),(1,x^(2),1)]:}," then "A^(-1)= |
|
Answer» `(1)/(4){:[(1,X,x^(2)),(z^(2),1,x),(x,x^(2),1)]:}` |
|
| 4792. |
If A , B are event such that P(A)=0.6, P(B)=0.4 and P(A cap B)=0.2, then find P(A | B) |
|
Answer» SOLUTION :A and B are EVENTS such that P(A)=0.6 P(B)=0.4,P `(A CAP B)`=0.2` P(A | B)= `(P(ACAPB))/(P(B))=0.2/0.4=2/4=1/2` |
|
| 4793. |
A diet of a sick personmust contains at least 48 units of vitamin A and 64 units of vitamin B. Two foods F_(1) and F_(2) are available. Food F_(1)costs Rs. 6 per unit andFood F_(2)costs Rs. 10 per unit. Oneunit of food F_(1)contains 6 units of vitamin A and 7 units of vitamin B. Oneunit of food F_(2) contains 8 units of vitamin A and12 unitsofvitamin B. Find the minimum cost for thediet that consists ofmixture of these two foodsand also meeting theminimum nutritionalrequirements. |
|
Answer» Solution :Let x units of food `F_(1)` andy units of food `F_(2)` be included in the diet of the sick person. Then their total costis Z Rs. `(6x + 10y)` We have to minimize the above cost function . Theconstraints are as per given the following table. `{:(,"Food "F_(1),"Food "F_(2),"Minimum"),(,(x),(y),"requirement"),("Vitamin A",6,8," "48),("Vitamin C",7,12," "64):}` Hence the CONSTRAINTS are ` 6x + 8y ge 48` ` 7x + 12y ge 64` Also the no. of units of food ` F_(1) and F_(2)` cannot be negative. ` x ge 0 and y ge 0` Hence themathematical formulation of given LPP is Minimize `Z = 6x + 10y` Subject to ` 6x + 8y ge 48` ` 7x + 12y ge 64` ` rArrx/(64//7) + y/(16/3) = 1` Plot these equations on GRAPH paper we get feasible region shaded on graph paper.  The vertices of the feasible region are ` C(64/7, 0), P ` and B (0, 6). P is the point of intersection of these lines ` 6x + 8y = 48` and ` 7x + 12y = 64` On solving these equations we get `P-=(4,3)` . Values of OBJECTIVE function at these vertices are ` Z(C) = 6 (64/7) + 10 (0) = (384)/7` ` = 54*85` ` Z(P) = 6(4) + 10(3)24 + 30 = 54` ` Z(B) = 6(0)+10(6) = 60` Minimum value of Z is 54 at point P(4,3) hence, 4units of food `F_(1) and 3` units of food `F_(2)` should be included in the diet of sick person to meet theminimal nutritional requirements, in order to have the minimum cost of Rs. 54. |
|
| 4795. |
A study has been done to determine whether or not a certain drug leads to an improvement in symptoms for patients with a particular medical condition. The results are shown in the following table : Based on this table, what is the probability that a patient shows improvement if it is known that the patient was given the drug ? |
|
Answer» 0.4375 |
|
| 4796. |
int_(e^(-1))^(e^(2))|(logx)/(x)|dx= |
|
Answer» `2/5` |
|
| 4798. |
Consider a DeltaABC in which sides AB and ACare perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of DeltaABC is (3/2, 5/2). The equation of the line in List I is of the form ax+by+c=0, where a,b,c in I. Match it with the corresponding value of c in list II and then choose the correct code. Codes : {:(a, b, c, d),(r, s, p, q),(s, r, q, p),(q, p, s, r),(r, p, s, q):} |
Answer» 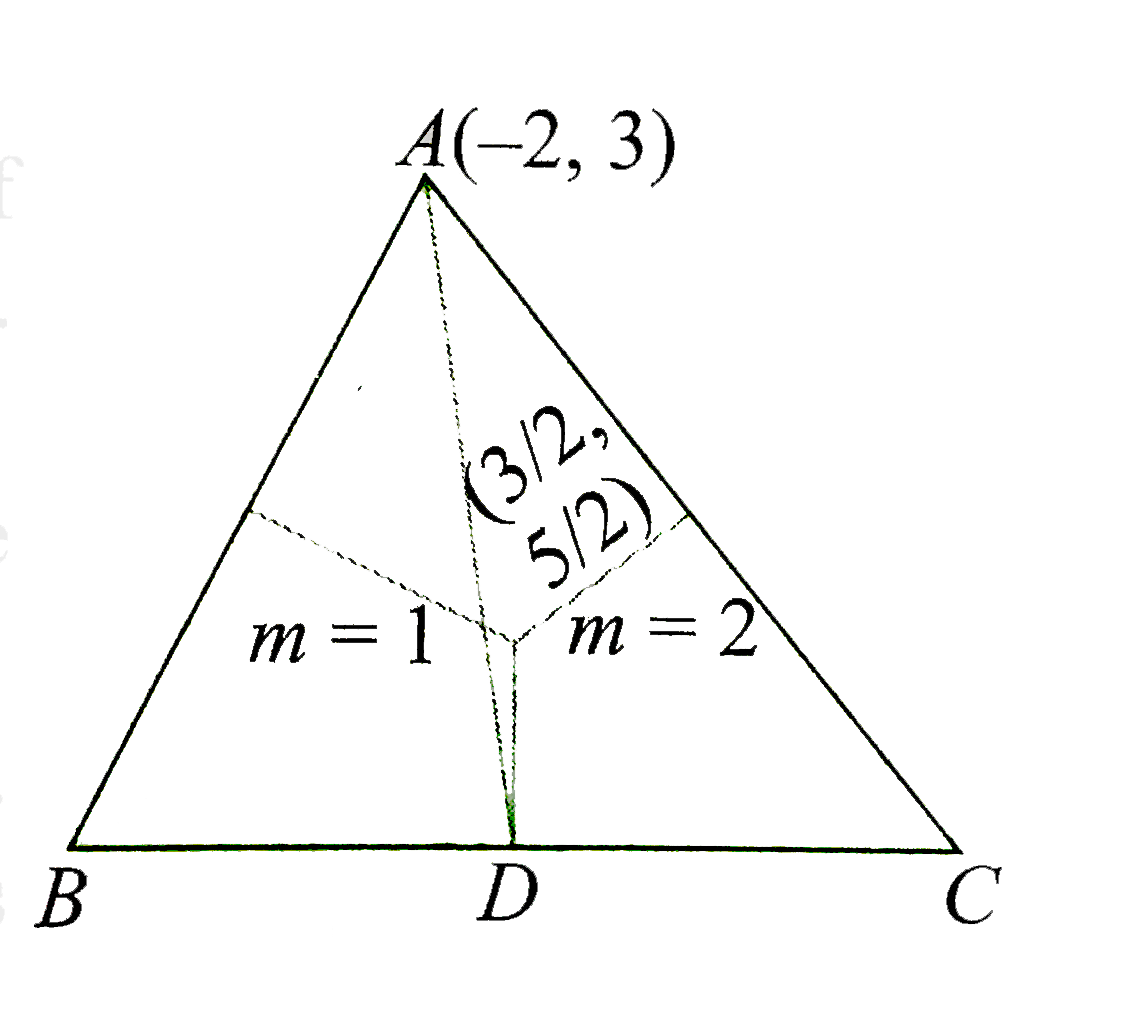 The perpendicular bisector of AB is parallel to x-y-4=0. THEREFORE, the slope is 1. It is passing through the circumcenter, i.e, (3/2, 5/2). Therefore, the line is x-y+1 =0. b. The perpendicular bisector of AC is B parallel to 2x-y-5=0. Therefore, the slope is 2. It is passing through the circumcenter, i.e., (3/2, 5/3). Therefore, the line is 4x-2y-1=0. c. The EQUATION of perpendicular bisector to AC is 2x-y-5=0. Therefore, the equation of AC can be`x+2y+lambda= 0.` It is passing through A(-2, 3). Therefore, `lambda = -4` Therefore, the equation of AC is x+2y-4=0. d. The image of A on the perpendicular bisector of AC is `(x+2)/(4) = (y-3)/(-2) = (-2(-8-6-1))/(16+4) = (3)/(2)` `therefore C-= (4, 0)` The image of A on the perpendicular bisector of AB is `(x+2)/(1) = (y-3)/(-1) = (-2(-2-3+1))/(1+1) = 4` Therefore, B is (2, -1). Therefore, the midpont of BC is D (3, -1/2). Hence, the median through A is 7x+10y-16=0. |
|
| 4799. |
If (3 + 7x - 9x^2)^n = a_0 +a_1x + a_2 x^2 + ……+a_(2n)x^(2n) prove the a_0 +a_1 +a_2 + ……+a_(2n) = 1 |
|
Answer» 0 |
|
| 4800. |
prove that (vec(a)+vec(b)).(vec(a)+vec(b))=|vec(a)|^(2)+|vec(b)|^(2), if and only if vec(a),vec(b) are perpendicular, given vec(a) ne vec(0), vec(b) ne vec(0). |
|
Answer» |
|