Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 601. |
Construct an isosceles triangle whose vertical angle is 60^(@) and the altitude is 4.6 cm. |
|
Answer» SOLUTION :Steps of construction : 1. Draw a line `DE` and take a point `P` on it. 2. Draw `angleAPE = 90^(@)` and cut `PA = 4.6 cm.` 3. Draw `angleCAP = angleBAP = (1)/(2) xx 60^(@) = 30^(@)` which meet `DE` at `C` and `B` respectively. `therefore DELTAABC` is the required triangle. 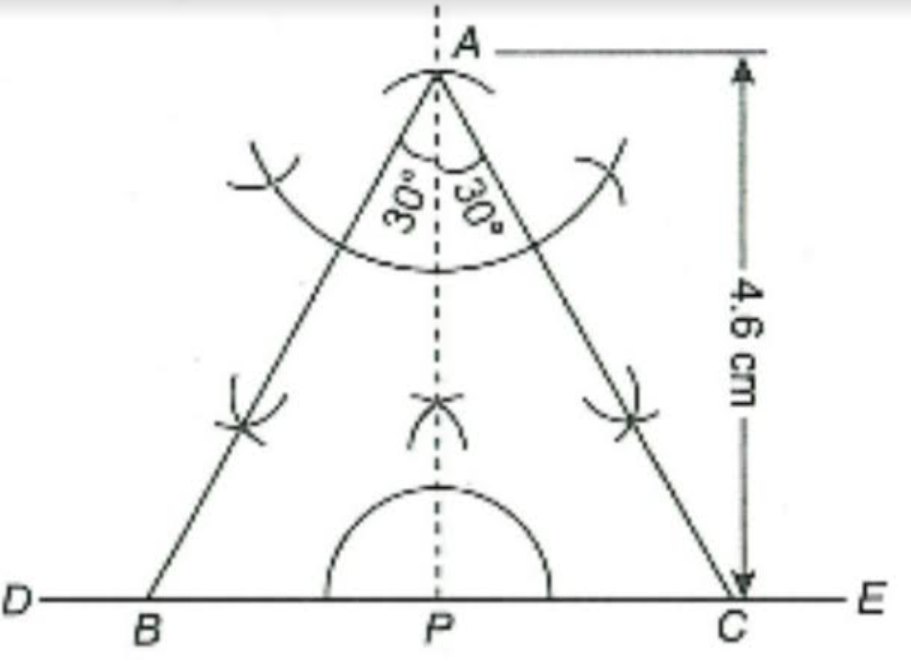 |
|
| 602. |
Factorise each of the following : 64m^(3) - 343 n^(3) |
|
Answer» |
|
| 603. |
Find the product (2a + b+c) (4a ^(2) + b ^(2) + c ^(2) - 2ab -bc -2ca) |
|
Answer» |
|
| 604. |
The perimeter of a rhombus is 144 cm and one of its diagonals measures 48 cm. Find the area of the rhombus. |
|
Answer» |
|
| 605. |
Check whether the polynomial q(t) = 4t^(3) + 4t^(2) - t-1 is a multiple of 2t +1. |
|
Answer» |
|
| 606. |
Mohit borrowed a certain sum at 5% per annum compound interest and cleared this loan by paying Rs 12,600 at the end of the first year and Rs 17,640 at the end of the second year. Find the sum borrowed. |
|
Answer» |
|
| 607. |
Construct a DeltaABC in which BC = 5 cm, angleB = 60^(@) and angleC = 45^(@). |
|
Answer» Solution :Steps of CONSTRUCTION : 1. Draw `BC = 5 cm.` 2. Draw `anglePBC = 60^(@)` and `angleQCB = 45^(@)`. 3. `BP` and `CQ` intersect at`A`. `therefore DeltaABC` is the required TRIANGLE. 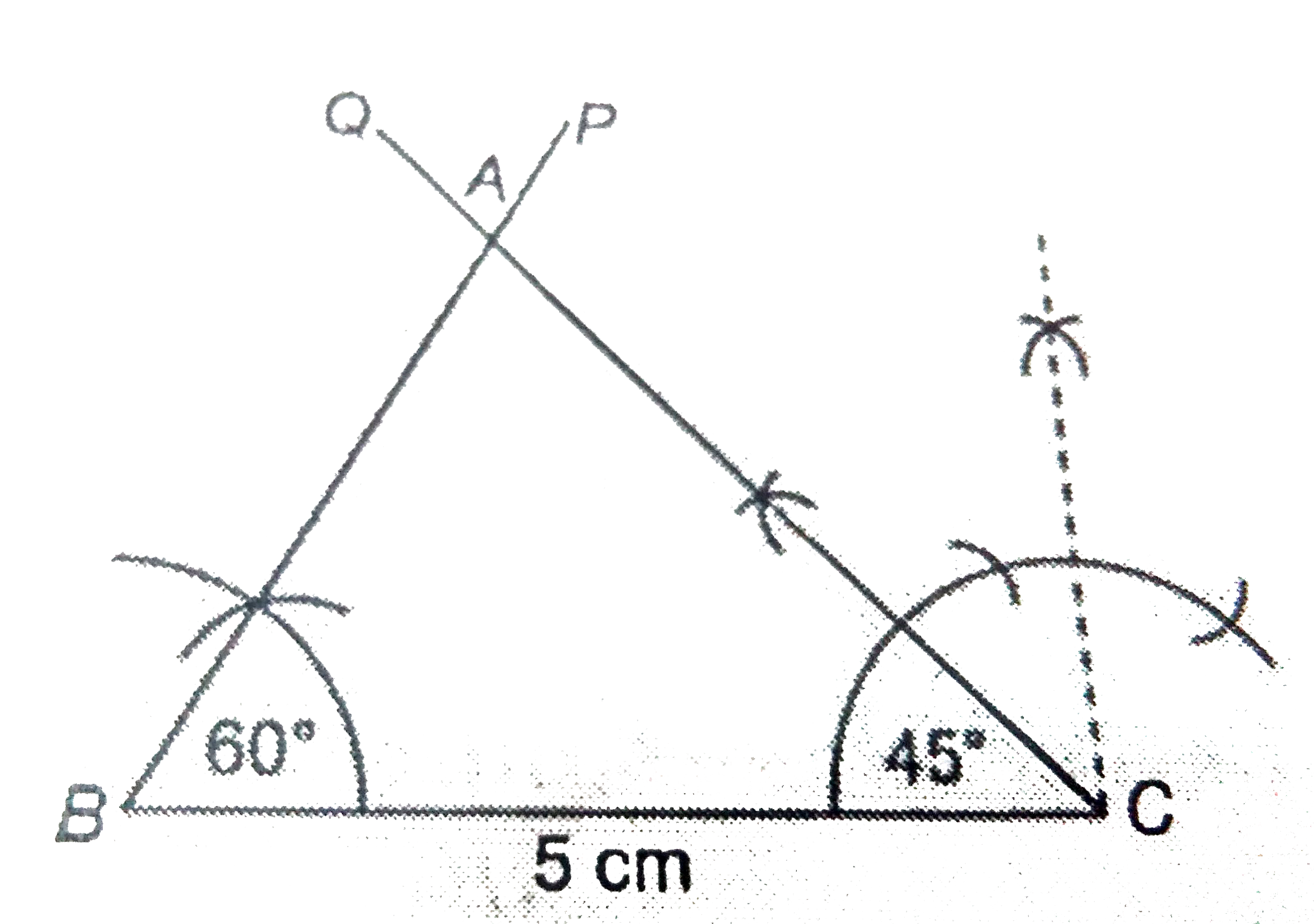
|
|
| 609. |
A Joker's cap is in the form of a right circular cone of base radius 7cm and height 27 cm. Find the area of the sheet required to make 10 such caps. |
|
Answer» |
|
| 610. |
A child playing with building blocks, which are of the shape of cubes, has built a structure as shown in the given figure. If the edge of each cube is 3 cm, find the volume of the structure built by the child. |
|
Answer» |
|
| 611. |
If the mid-points of AB, BC and CA of the DeltaABC are D, E and F respectively, P and Q are also the mid-points of DE and EF respectively. Then PQ = |
| Answer» Answer :C | |
| 612. |
Find the surface area of a sphere of diameter : (i) 14 cm(ii) 21 cm(iii) 3.5 m |
|
Answer» (ii) 1386 `cm^(2)` (III) 38.5 `m^(2)` |
|
| 613. |
The radius and height of a cone are 7 cm and 3 cm respectively. Then, the volume of the cone is ……… cm^(3). |
|
Answer» 154 |
|
| 614. |
PQ and RS are two equal chords of a circle with centre O such that anglePOQ=70^(@), then angleORS = . . . . . . . . . . |
| Answer» Answer :C | |
| 615. |
Construct a Delta ABC in which BC=6 cm, angleB=60^(@) and (AC-AB)=2 cm. Measure AC and AB. Justify your construction. |
|
Answer» SOLUTION :STEPS OF CONSTRUCTION (i) Draw `BC=6` cm. (ii) Construct `angle CBX=60^(@)` (iii) Produce `XB` downwards to a POINT `X'`. (iv) Set off `BD=2` cm along `BX'`. (v) JOIN `CD`. (vi) Draw the perpendicular bisector of `CD`, meeting `BX` at `A`. (vii) Join `AC`. Then, `Delta ABC` is the required triangle. VERIFICATION : On measuring, we FIND that `AC=5.4` cm and `AB=3.4` cm. `:. (AC-AB)=(5.4-3.4)cm =2` cm. Justification : Since `A` lies on the perpendicular bisector of `CD`, we have `AD=AC`. Now, `BD=2` cm `implies AD-AB=2` cm `implies AC-AB=2 cm ""[ :' AD=AC]`. Hence, `Delta ABC` is the required triangle. 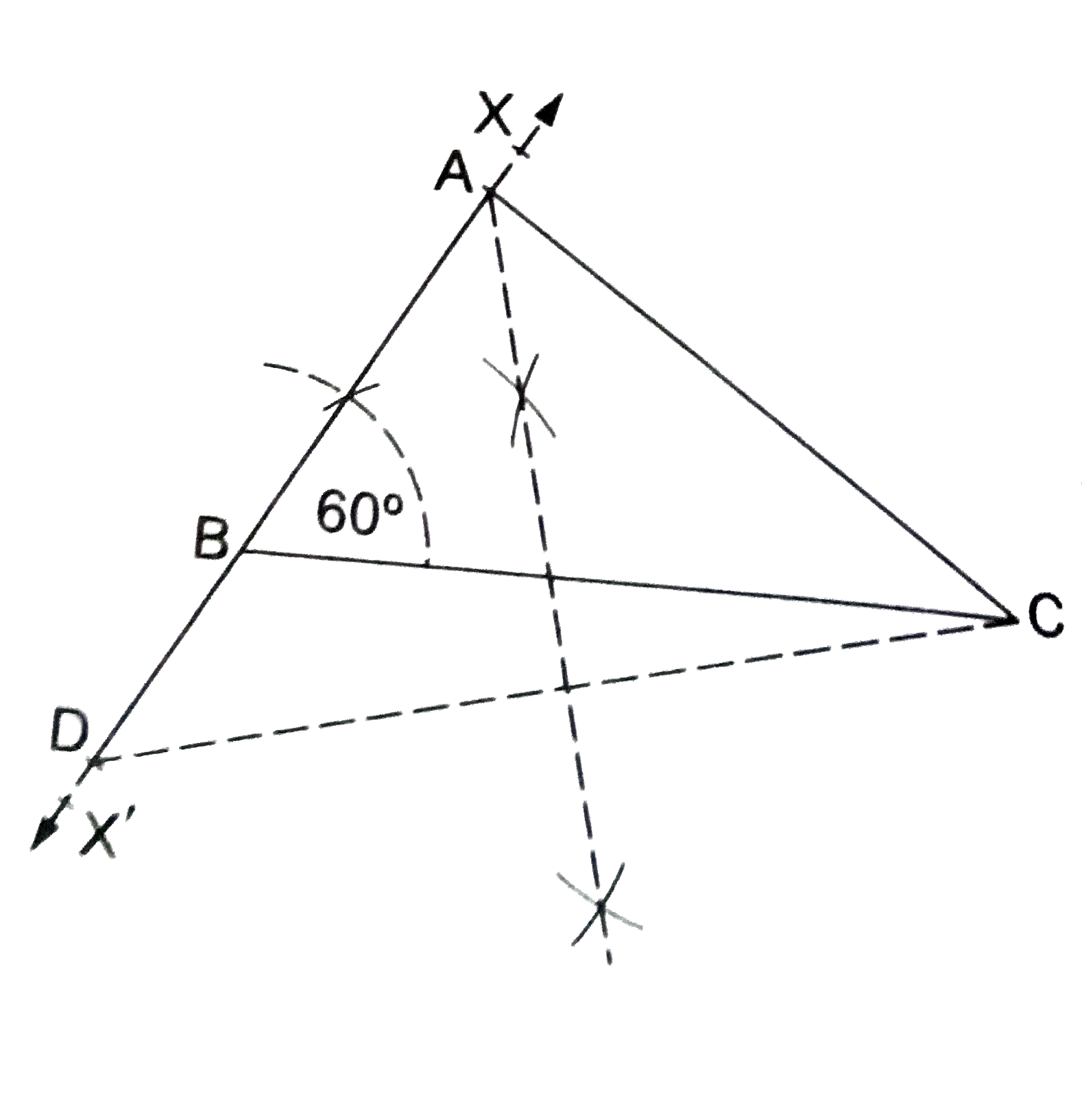
|
|
| 617. |
Find for solutions of each of the following equation : 2x - y = 12 |
|
Answer» |
|
| 619. |
A number is 27 more than the number obtained by reversing its digits. If its unit’s and ten’s digits are x and y respectively, write the linear equation representing the above statement. |
|
Answer» |
|
| 620. |
The measure of the supplementary angle of an angle with measure 70^(@) is ........... . |
|
Answer» `20^(@)` |
|
| 621. |
A hemispherical bowl made of brass has inner diameter10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16per100"\ "c m^2. |
|
Answer» |
|
| 623. |
Find the mean and median of the data : 35, 48, 92, 76, 64, 52, 51, 63 and 71. If 51 is replaced by 66, what will be the new median ? |
|
Answer» |
|
| 624. |
Fill in the blands so as to make each of the following statements true : In DeltaABC,angleA=40^(@) and angleC=50^(@). Then the smallest side of DeltaABC is ………. |
|
Answer» |
|
| 625. |
The measure of the complementary angle of an angle with measure 40^(@) is ............. |
| Answer» | |
| 626. |
The total surface area of a hemisphere is 4158 cm^(2). Find its diameter. |
|
Answer» |
|
| 627. |
Determine which of the following polynomials has (x+1) a factor : x^(3) - x^(2) - (2+sqrt(2))x + sqrt(2) |
|
Answer» |
|
| 628. |
Write the following based on the graph (i) The ordinate of L (ii) The ordinate of Q (iii) The point denoted by (-2,-2) (iv) The point denoted by (5,-4) (v) The abscissa of N (vi) Theabscissa of M |
|
Answer» |
|
| 629. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 400","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will need to be replaced after it has covered somewhere between 4000 km and 14000 km ? |
|
Answer» |
|
| 630. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 400","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will last more than 9000 km ? |
|
Answer» |
|
| 631. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 400","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will need to be replaced before it has covered 4000 km ? |
|
Answer» |
|
| 632. |
The mean monthly salary of 10 people is Rs. 2,890. One more person whose monthly salary is Rs. 3,000 has also been taken into consideration. Find the mean monthly salary of all the 11 people. |
|
Answer» |
|
| 633. |
Find the value of x if (i) 25^(2x - 3) = 5^(2x + 3)(ii) (4)^(2x - 1) - (16)^(x - 1)=384 |
|
Answer» |
|
| 634. |
A right triangle when one side is 3.5cm and sum of other sides and the hypotenuse is 5.5cm. |
|
Answer» Solution :Let given right triangle be `ABC` . Then , given `BC` = `3.5cm angleB = 90^(@)` and SUM of other side and hypotenuse i.e., `AB + AC = 5.5cm` To construct `DeltaABC` use the following STEPS (i) Draw the base `BC = 3.5cm` (ii) Make an angle `XBC` = `90^(@)` at the point `B` of base `BC`. (III) Cut the line segment BD EQUAL to `AB+ AC` i.e., `5.5cm` from the ray XB. (iv) Join DC and make an `angleDCY` equal to `angleBDC` . Let Y intersect BX at A. Thus , `DeltaABC` is the required triangle. Justification Base BC and `angleB` are drawn as given. In `DeltaACD, angle ACD = ANGLEADC` [by construction] `:.` AD = AC...(i) [sides opposite to equal angle are equal] Now `AB = BD - AD = BD- AC`[from Eq. (i)] `rArr BD = AB + AC` Thus , our construction is justified. 
|
|
| 635. |
Classify the following as linear, quadratic and cubic polynomials : 3t |
|
Answer» |
|
| 636. |
Without actually dividing find which of the following are terminating decimals. (41)/(42) |
|
Answer» |
|
| 637. |
Construct a rhombus each of whose sides is of length 3.4 cm and one of its angles is 45^(@). |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw a line segment `AB=3.4` CM. (ii) Construct `angleBAX=45^(@)`. (iii) Along `AX` SET off `AD=3.4` cm. (iv) Construct `angleABY=135^(@)`. (v) Along `BY` set off `BC=3.4` cm.  (vi) Join `CD`. Then, `ABCD` is the REQUIRED rhombus. |
|
| 638. |
Sreedher borrowed Rs 3500 at 6% per annum for 3 years under simple interest. But, after one year he was asked to pay compound interest for the remaining two years on the sum borrowed initially. How much additional interest Sreedhar has to pay? |
|
Answer» Rs 10 II) Find SI and CI as per the GIVEN data. iii) Find the difference between CI and SI. |
|
| 639. |
Factorise each of the following (i) 8a ^(3) + b^(3) + 12a ^(2)b + 6ab ^(2) (ii) 8a ^(3) - b ^(3) -12a ^(2) b+ 6ab ^(2) (iii) 1- 64 a ^(3) -12a + 48 a ^(2) (iv) 8p^(3) - (12)/(5) p^(2) + (6)/(25) p- (1)/(125) |
|
Answer» (ii) `(2a -b) ^(3)` (iii) `(1- 4a ) ^(3)` (iv) `(2P - (1)/(5)) ^(3)` |
|
| 640. |
The mean of 5 numbers is 18. If one number is excluded, the mean of remaining numbers becomes 16. Find the excluded number. |
|
Answer» |
|
| 641. |
Construct ana ngle of 45^(@), using ruler and compasses only. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Construct `angleAOB=90^(@)`, as EXPLAINED in EXAMPLE 7. (ii) DRAW the BISECTOR OC of `angleAOB`. Then, clearly, `angleAOC=45^(@)`. Hence, `angleAOC` is the required ANGLE of measure `45^(@)` 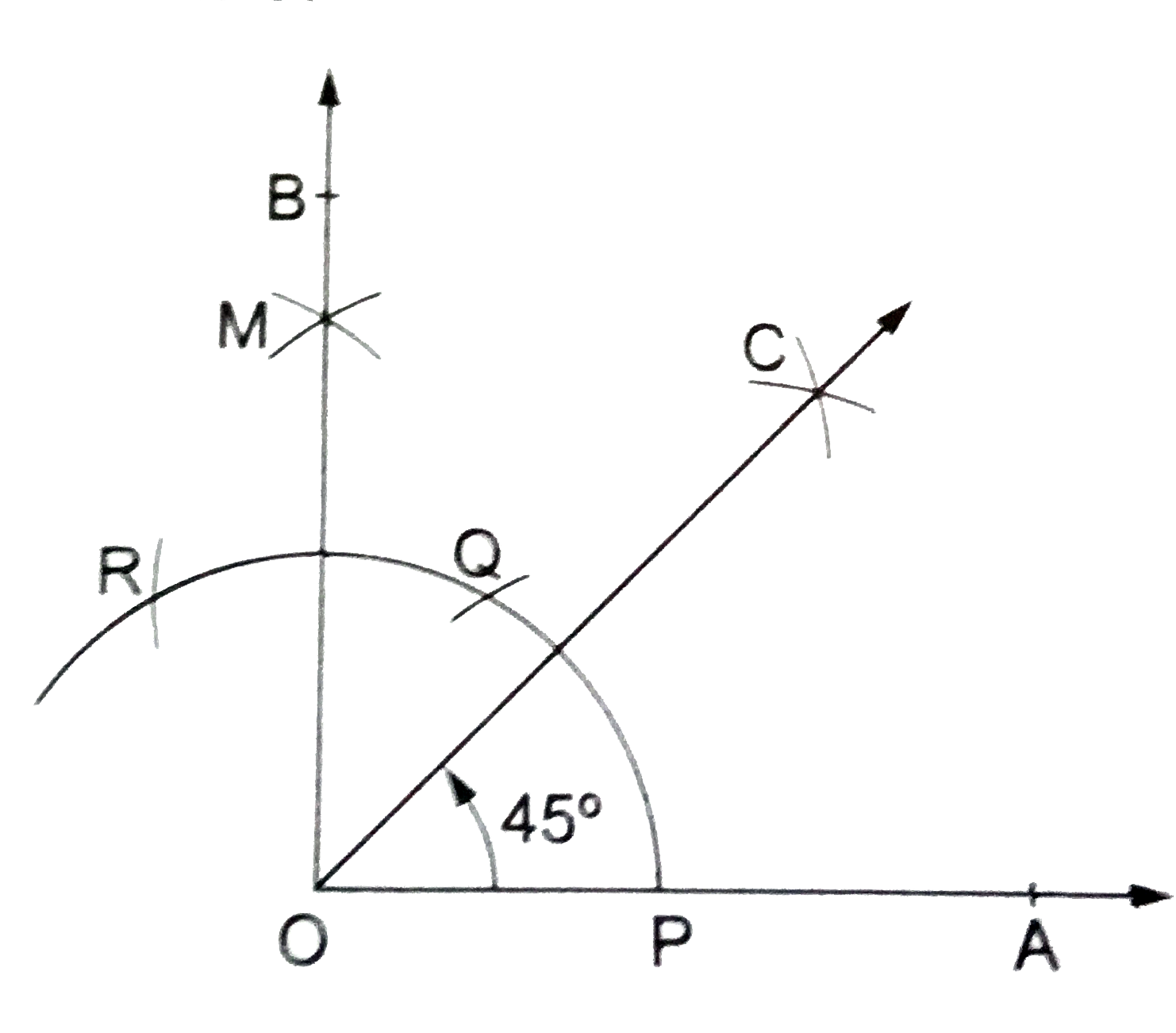
|
|
| 642. |
Draw the graph of the equations x-y+ 1 =0and3x +2y -12=0.Determine the coordinates of the vertices of the triangle formed by the lines and the x-axis and shade the triangular region. |
|
Answer» |
|
| 643. |
In the given diagram PQRS is a parellelogram. angleS=4x-60angleQ=30-x. Find the angles of P and R . |
|
Answer» |
|
| 644. |
Find the Total Surface Area and the Lateral Surface Area of a cuboil whose dimensions are length = 20 cm, breadth = 15 cm, height = 8 cm |
|
Answer» |
|
| 646. |
x^(2) - 2 + (1)/(x^(2)) = ………… |
|
Answer» `(x+(1)/(x))(x-(1)/(x))` |
|
| 647. |
If H.M and G.M of two positive real numbers are 13 and 9 respectively, then find their A.M. |
| Answer» | |
| 648. |
Two of the vertices of a triangle ABC and A (1,1) B-1,3) and the area of Delta ABC is 6 sq units. If P is the centroid of the Delta ABC, then find the locus of P. |
|
Answer» `2X - y + 1 = 0` Area of `Delta PAB` is given by `(1)/(2) |{:(x_(1) - x_(2),x_(2) - x_(3)),(y_(1) - y_(2),y_(2) - y_(3)):}|` |
|
| 649. |
Write the mark wise frequencies in the following frequency distribution table. |
|
Answer» |
|
| 650. |
Construct a DeltaABC in which base BC = 5.2 cm, angleABC = 50^(@) and AB - AC = 2 cm. |
|
Answer» SOLUTION :STEPS of construction : 1.Draw `BC = 5.3 CM.` 2. Construct `anglePBC = 50^(@)` and cut `BP = 2 cm.` 3. JOIN `PC.` 4. Draw the perpendicular bisector of `PC` which intersect `BP` produced at `A.` 5. Join `AC.` `THEREFORE DeltaABC` is the required triangle. 
|
|