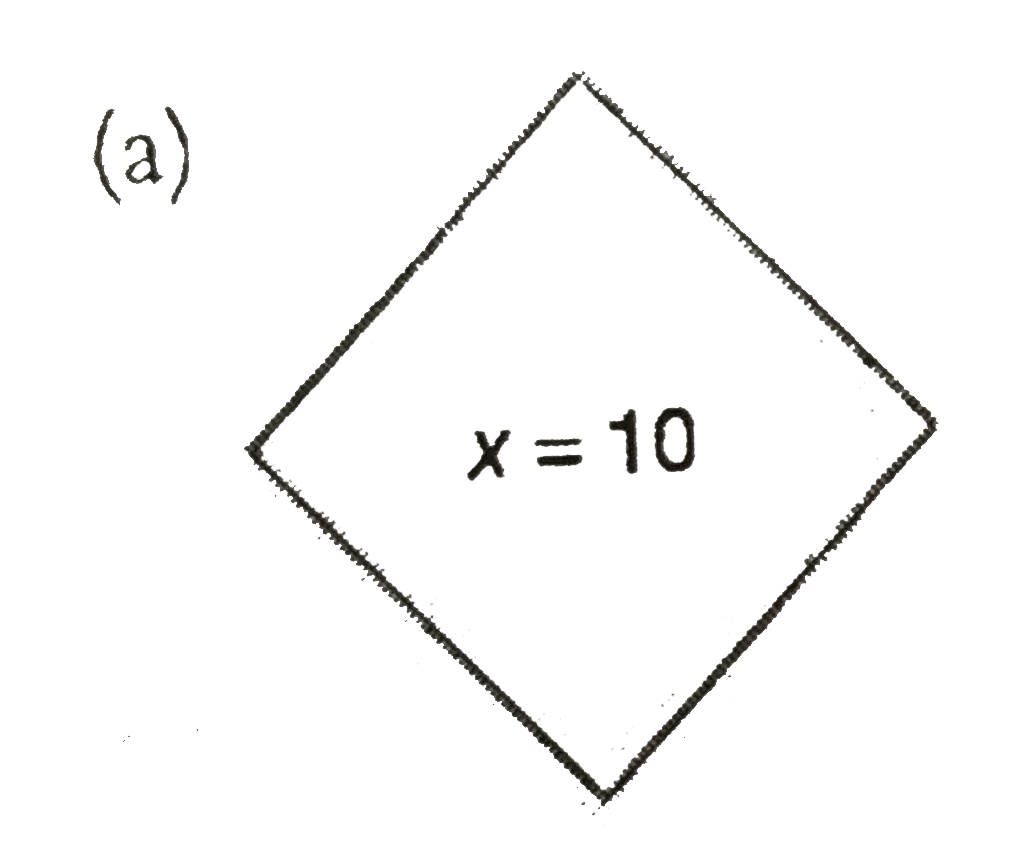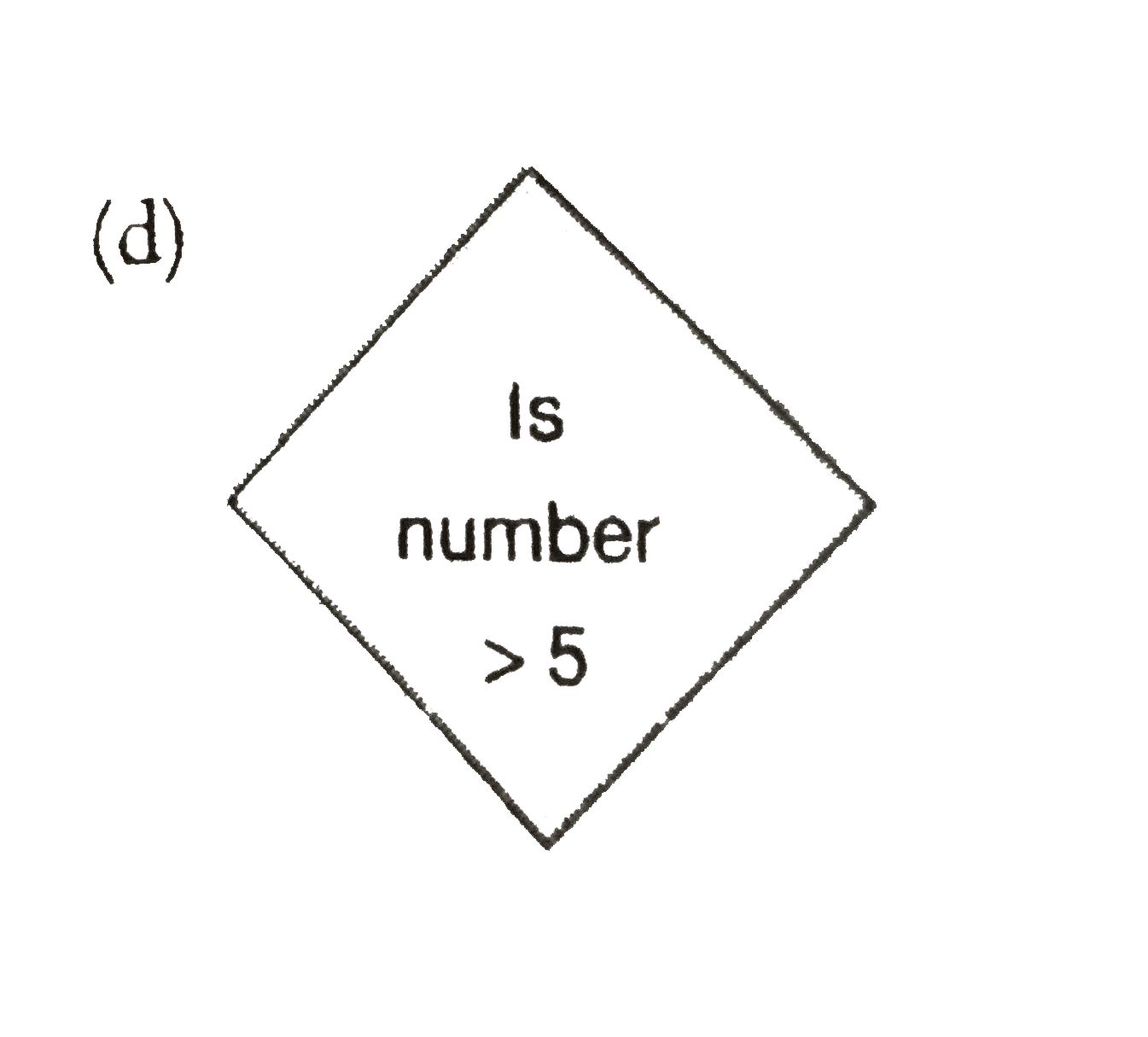Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1451. |
Factorise the following using appropriate identities : x^(2) - (y^(2))/(100) |
|
Answer» |
|
| 1452. |
Draw the graph of theequation, 2x-3y=5. From your graph , find (i) the value of y when x=4 and (ii) the value of x when y=3. |
|
Answer» |
|
| 1453. |
Represent (8)/(5) and (-8)/(5) on the number line |
|
Answer» |
|
| 1455. |
ABC is a triangle . D is a point of AB such that AD=(1)/(4)AB and E is a point on AC such that AE=(1)/(4)AC. If DE =2cm find BC. |
|
Answer» |
|
| 1456. |
Construct a triangle whose sides are 3.6 cm, 3 cm and 4.8 cm. Bisect the smallest angle and measure each part. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) DRAW `AB=3.6` cm. (ii) With `A` as centre and `3 cm` as RADIUS, draw an arc. (iii) With `B` as centre and `4.8` cm as radius, draw another arc, cutting the previous arc at `A`. (iv) Join `AC` and `BC`. Then, `Delta ABC` is the REQUIRED triangle. (v) Clearly, the angle opposite to the smallest side is smallest. So, `angleB` is the smallest angle. (VI) So, we draw `BD,` the bisector of `angleB`. On measuring, we find that `angleABD=angleCBD=20^(@)`. 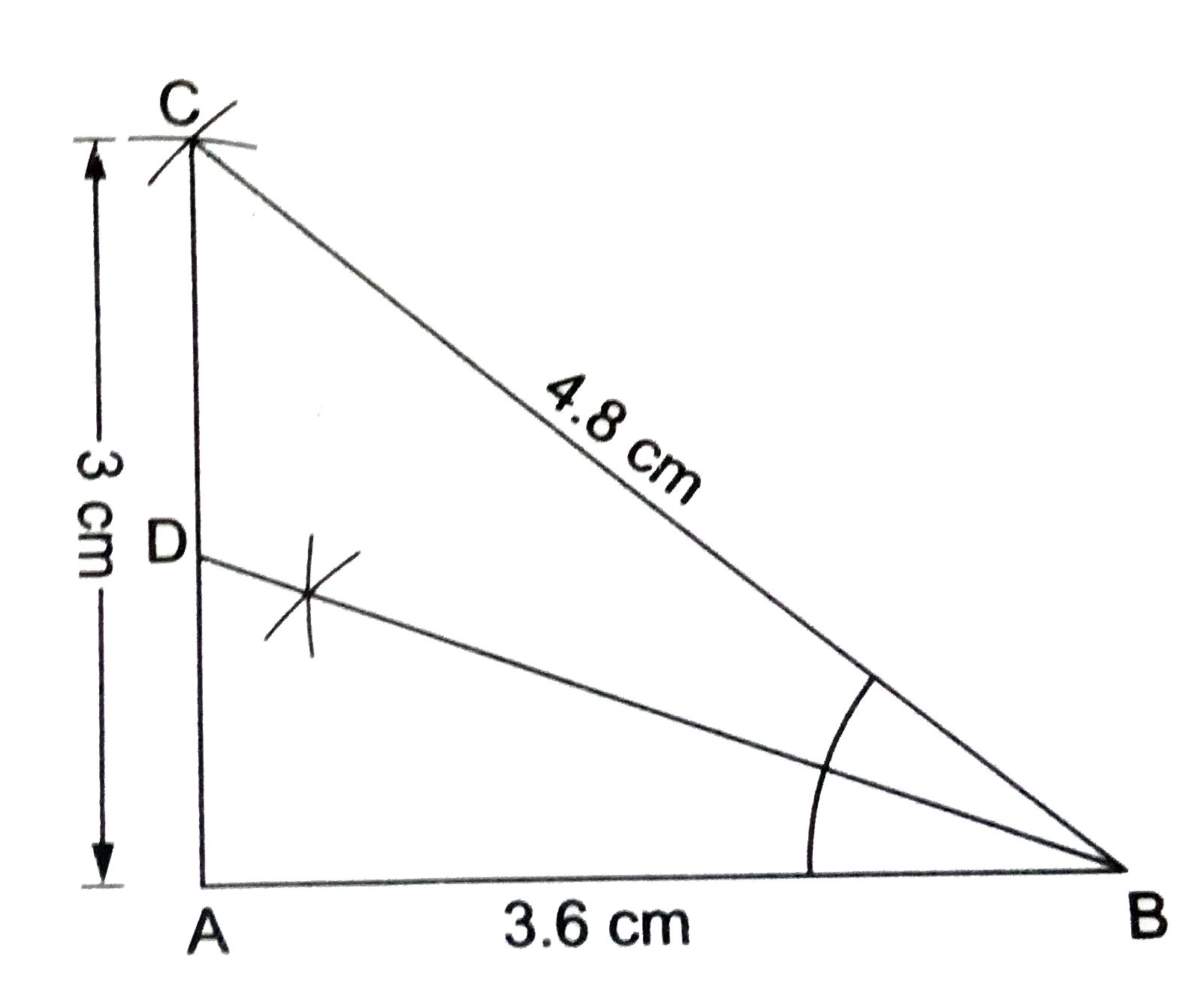
|
|
| 1457. |
Classify the following numbers as rational or irrational. (1)/(sqrt3) |
|
Answer» |
|
| 1458. |
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: ( i ) AD bisects BC ( ii) AD bisects angle A |
|
Answer» |
|
| 1459. |
Which of the following points lie on the axes? Also name the axis (i) (-5,-8) (ii) (0,13) (iii) (4,-2) (iv) (-2,0) (v) (0,-8) (vi) (7,0) (vii) (0,0) |
|
Answer» (V) (0,-8) Y-axis (vi) (7,0) X-axis (VII) (0,0) on both the axis. |
|
| 1460. |
Fill in theblanks:All pointlying inside/outside a circle are called ... points/... points.Circlehaving the same centre and different radii are called ... circles.A pointwhose distance from the centre of a circle is greater than its radius lies in .... of the circle.Acontinuous piece of a circle is .... of the circle.The longestchord of a circle is a ......of the circle.An arc is a......... when its ends are the ends of a diameter.Segment ofa circle is the region between an arc and ... of the circle.A circledivides the plane, on which it lies, in .... parts. |
|
Answer» |
|
| 1461. |
If A={:[(2,1),(-3,4),(5,2)]:},B={:[(-1,2),(4,-1)]:}andC={:[(-1,5),(-5,6)]:}, then verify whether A(B-C)=AB-AC. |
| Answer» | |
| 1462. |
Construct a rectangle whose adjacent sides are of lengths 5cm and 3.5cm . |
|
Answer» Solution :We know that each angle of a rectangle is right angle (i.e., `90^(@)`) and its opposite sides are equal and parallel. To construct a rectangle whose adjacent sides are of lengths `5cm` and `3.5cm` use the following steps (i) Draw a line segment `BC` of length `5cm` . (ii) Now, GENERATE an angle of `90^(@)` at points `B` and `C` of the line segment `BC` and plot the parallel lines `BX` and `CY` at these points. (iii) Cut AB and CD of length `3.5cm` from BX and CY, respectively. (IV) Draw and angle `90^(@)` at one of the POINT A or D and join both points by a line segment AD of length 5cm. THUS , ABCD is the required rectangle with adjacent sides of length 5cm and `3.5cm` 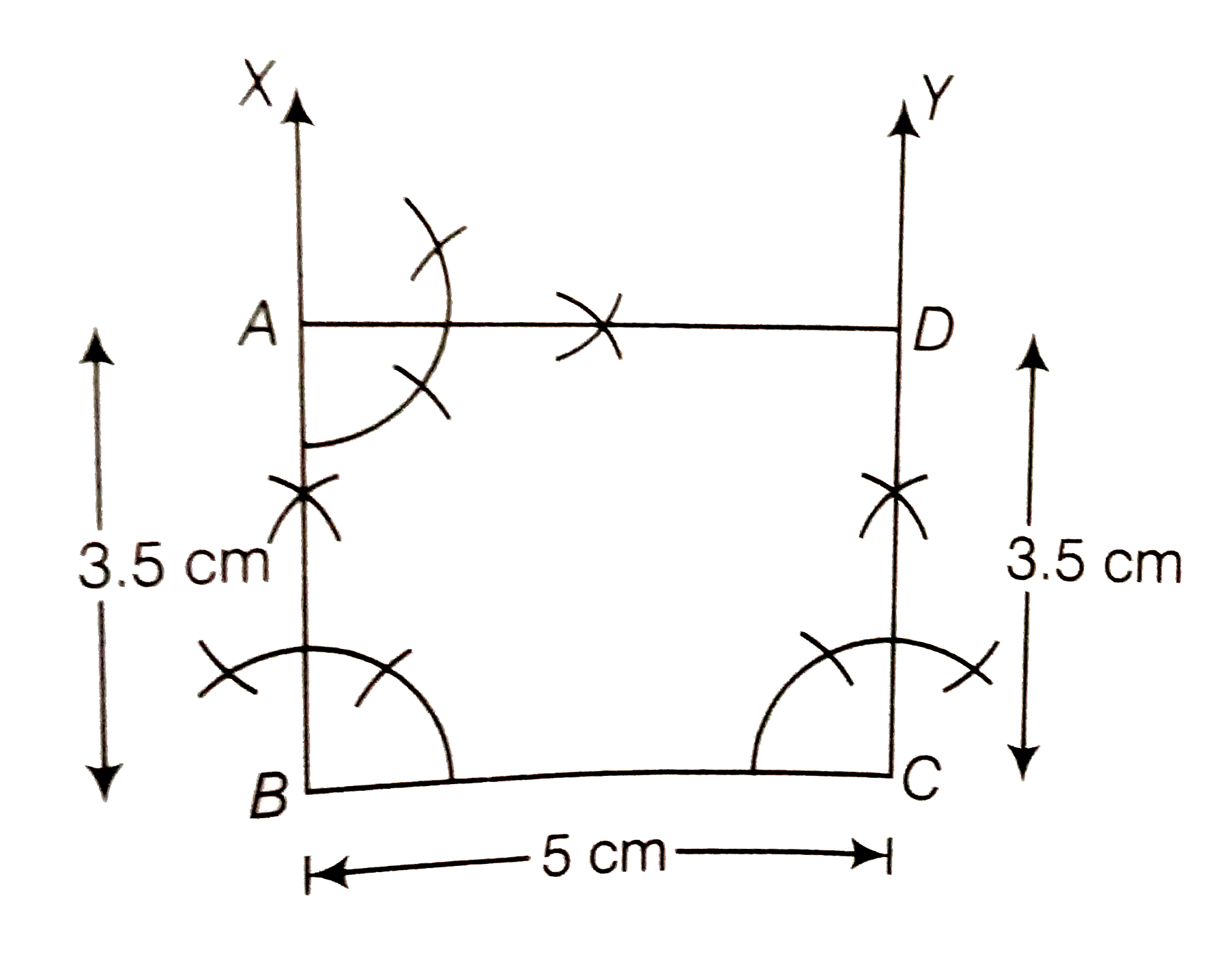 Alternate Method To construct a rectangle `ABCD` whose adjacent sides are of lengths `5 cm` and `3.5cm`, use the following steps (i) Draw a line segment `BC` of length 5cm. (ii) Now, draw an `angleXBC - 90^(@)` at point `B` of line segment `BC`. (iii) Cut a line segment AB = `3.5cm` from the ray `BX` and join `AC`. (iv) Now, from A, point D is at a distance of 5cm. So, having `A` as centre draw an arc of radius 5cm. (v) From C, point D is at a distance of `3.5cm` . So, having C as centre draw an arc of radius `3.5cm` which intersect previous arc (obtained in STEP iv) at D. (vi) join `AD` and `CD`. Thus, `ABCD` is the required rectangle with adjacent sides of length `5cm` and `3.5cm` . 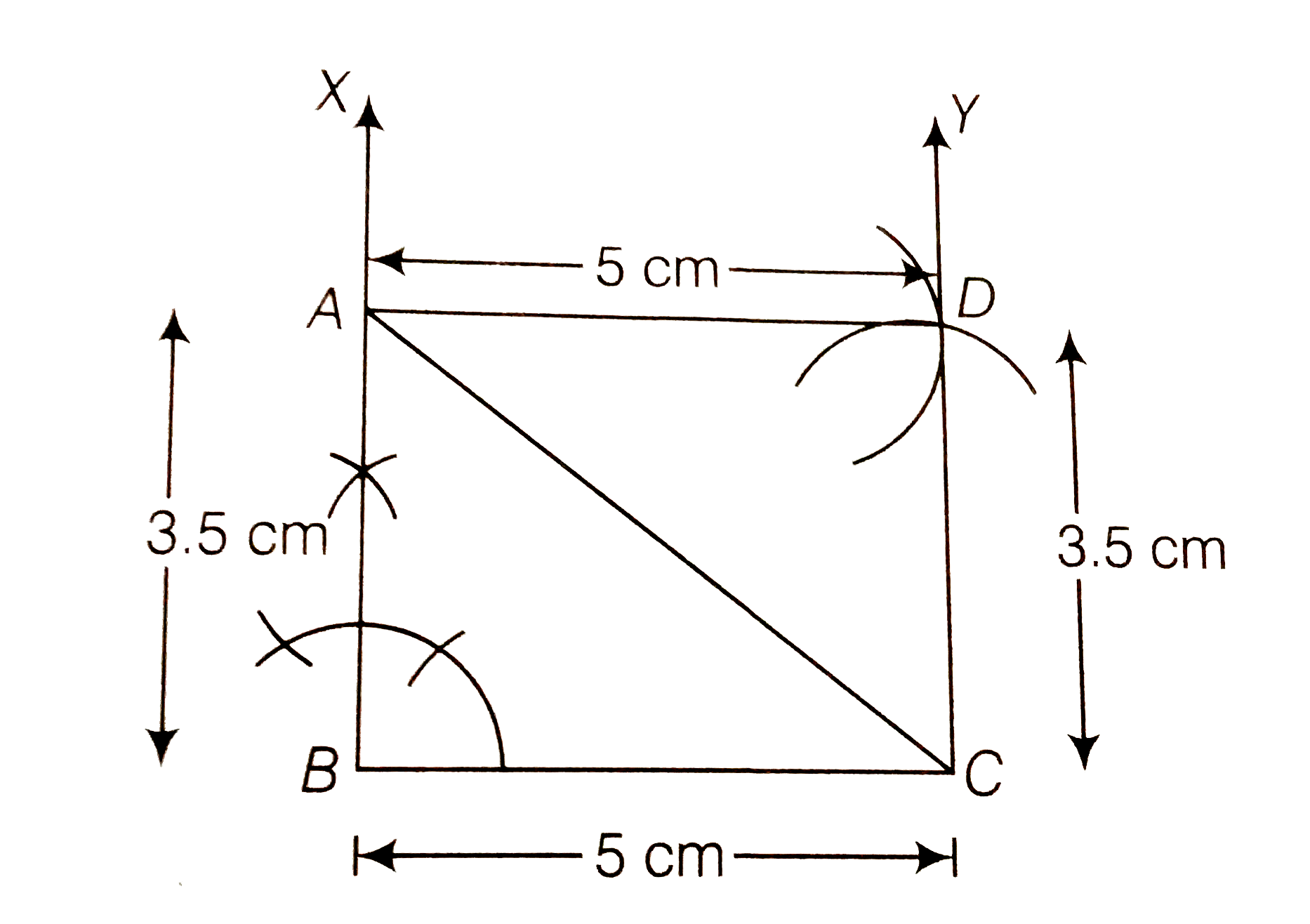
|
|
| 1463. |
If the factors of 5x^(2)-18x+9 are (ax+b), (x+b) then the value of a & b of are ...........& ..........respectively. |
|
Answer» |
|
| 1464. |
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs. 16 per 100 cm^(2). |
|
Answer» |
|
| 1465. |
State whether the following statements are true or false. Justify your answers. (ii) Every rational number is a real number. |
|
Answer» |
|
| 1466. |
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic. |
|
Answer» <P> Solution :Given ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawm that it intersect AD at P and BC at QTo PROVE Points P, Q, C and D are con-cyclic. 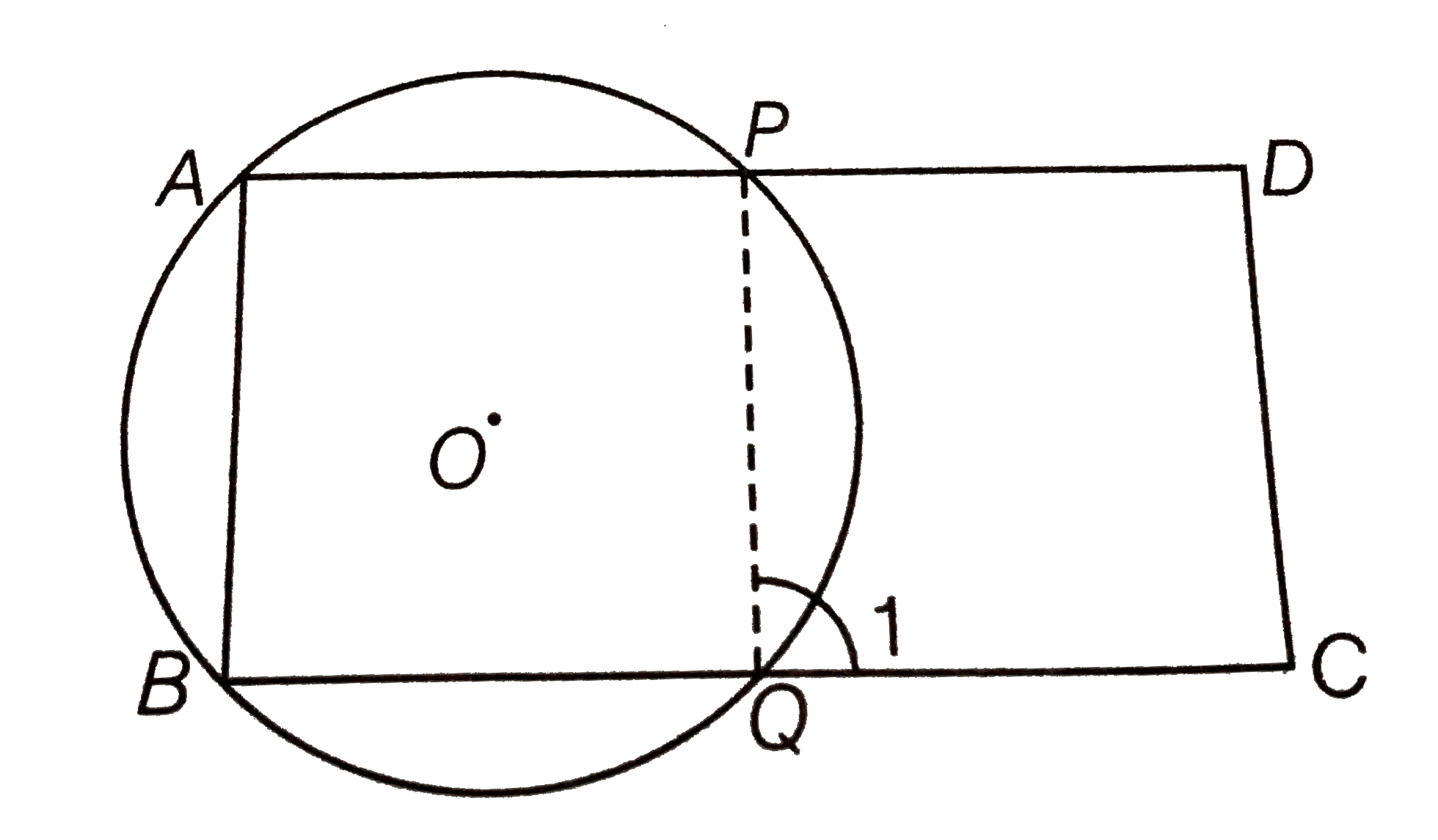 Construction Join PQ Proof `angle1=angleA` [exterior angle PROPERTY of cyclic QUADRILATERAL] But` angleA=angleC` [opposite angles of a parallelogram] `:. angle1=angleC` ...(i) But `angleC=angleD=180^(@)` [sum of cointerior angles on same side is `180^(@)`] `rArr angle1+angleD=180^(@)`[from Eq. (i)] Thus, the quadrilateral QCDP is cyclic. So, the points P, Q ,C and D are con-cyclic. |
|
| 1467. |
If 2 is a zero of the polynomial p (x) = 2x ^(2) - 3x + 7a, then find the value of a. |
|
Answer» |
|
| 1468. |
If sqrt(3)tan2theta=3 and 0^(@) lt theta le 90^(@), find the value of 3sqrt(3)costheta+2sintheta-6tan^(2)theta. |
|
Answer» |
|
| 1469. |
Out of 25 numbers, the mean of 15 numbers is 36 and the mean of the remaining numbers is 26, find the mean of all the 25 numbers. |
|
Answer» |
|
| 1470. |
In the following figure, OAB is a triangle and AB////DC. If the area of DeltaCAD=140cm^(2) and the area of DeltaODC=172cm^(2), find (i) the area of DeltaDBC (ii) the area of DeltaOAC (iii) the area of DeltaODB. |
|
Answer» |
|
| 1471. |
When a polynomial 2x ^(3) + 3x ^(2) + ax + b is divided by (x-2) leaves remainder 2, and (x +2) leaves remainder -2. Find a and b. |
|
Answer» |
|
| 1472. |
The ratio of radii of two cones is 2 : 3 and the ratio of their heights is 9 : 4. Then, the ratio of their volumes is ……… . |
|
Answer» `1:1` |
|
| 1473. |
Anil opened a recurring deposit account with Axis Bank for n year .He deposited Rs 800 in every month.The bank paid him Rs 10784n on maturity The rate of interest was 8% per annum .Find n |
|
Answer» 3 `SI(in RS) =800((12n)(12n+1))/(2)(1/12)(8/100)` `=32n (12n+1) Amount paid by THEBANK (in Rs) =(12n)(800)+32n(12n+1) =960n+32n(12n+1) Given ,9600 n + 32n (12n+1) `RARR 32n(12n+1)=10.784n=1184n` `rarr 12n+1=37rarr n=3` |
|
| 1474. |
Find five rational numbers between 1 and 2. |
|
Answer» |
|
| 1475. |
Assume that a dart will hit the dart board and each point on the dart board is equally likely to be hit in all the three concentric circles where radii of concetric circles are 3 cm, 2 cm and 1 cm as shown in the figure below. Find the probability of a dart hitting the board in the regionA. (The outer ring) |
|
Answer» |
|
| 1476. |
Express 0.bar(5) in the form of (p)/(q). |
|
Answer» |
|
| 1478. |
Ashok bought Rs.135 shares of a company at premium. If the company provides the same premium amount as discount, then its market value will decrease by 50%. Find the premium. (in Rs.) |
|
Answer» 40 |
|
| 1479. |
Classify the following as linear, quadratic and cubic polynomials : 7x^(3) |
|
Answer» |
|
| 1480. |
Find the remainder when x^(3) + 3x^(2) + 3x+1 is divided by : x + pi |
|
Answer» |
|
| 1481. |
Find two irrational numbers between 0.7 and 0.77 |
|
Answer» |
|
| 1482. |
In the given figure, if AB"||"DE, angleBAC=35^(@) and angleCDE=53^(@), find angleDCE. |
|
Answer» |
|
| 1483. |
Factorise : 8a^(3) + 27b^(3) + 36a^(2)b + 54 ab^(2) |
|
Answer» |
|
| 1484. |
Express each of the following decimals in (p)/(q) form where qne0 and p, q are integers 3.25 |
|
Answer» |
|
| 1485. |
Classify the following numbers as rational or irrational. 30.2323342345… |
|
Answer» |
|
| 1486. |
Two sides of a triangle measure 9 cm and 10 cm. If the perimeter of the triangle is 36 cm, then its area is …………..cm^(2) |
|
Answer» 17 |
|
| 1488. |
The population of a town in China inreases by 20% every year If its present popularion is 2,16,000 , find: its population 2 years ago. |
|
Answer» |
|
| 1489. |
Factorise : (1)/(9)a^(2) - (1)/(49)b^(2) |
|
Answer» |
|
| 1490. |
The sides containing right angle of a right angled triangle are 8 cm and 6 cm. It is rotated about the side of 8 cm. Find the total surface area of the formed solid. |
| Answer» | |
| 1491. |
Roja invested Rs 6000 in a bank, which paid compound interest, interest being compounded semi annually. She received Rs 10,368 after 18 months from the bank. Find the rate of interest. (per annum) |
| Answer» SOLUTION :`40%` | |
| 1493. |
Complete the hexagonal and star shaped Rangolies [see figure (1) and (2) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ? |
|
Answer» |
|
| 1495. |
A die is thrown. Find the probability of getting:an even number |
|
Answer» `1/6` |
|
| 1496. |
Find the measure of all the angles of a parallelogram, if one angle is 24^(@) less than the twice of the smallest angle. |
|
Answer» |
|
| 1497. |
Construct a triangle ABC, in which base BC =6 cm, AB+AC=9 cm and angleABC=45^(@) |
|
Answer» Solution :Step 1: Draw `BC = 6 cm.` Step 2: Draw `bar(BX)`, such that `angleCBX=45^(@)`. Step 3: With `B` as the center and the radius as `AB+AC=9` cm, draw an arc to meet `bar(BX)` at `D`. JOIN `CD`. Step 4: Draw the perpendicular bisector of `bar(CD)` to interest `bar(BD)` at A. Join `CA`. `triangleABC` is the required triangle. Proof. As AQ is the perpendicular bisector of `CD`, `ACD` is an ISOSCELES triangle, hence `AD = AC` and `AB+AC=AB+AD=9cm.` 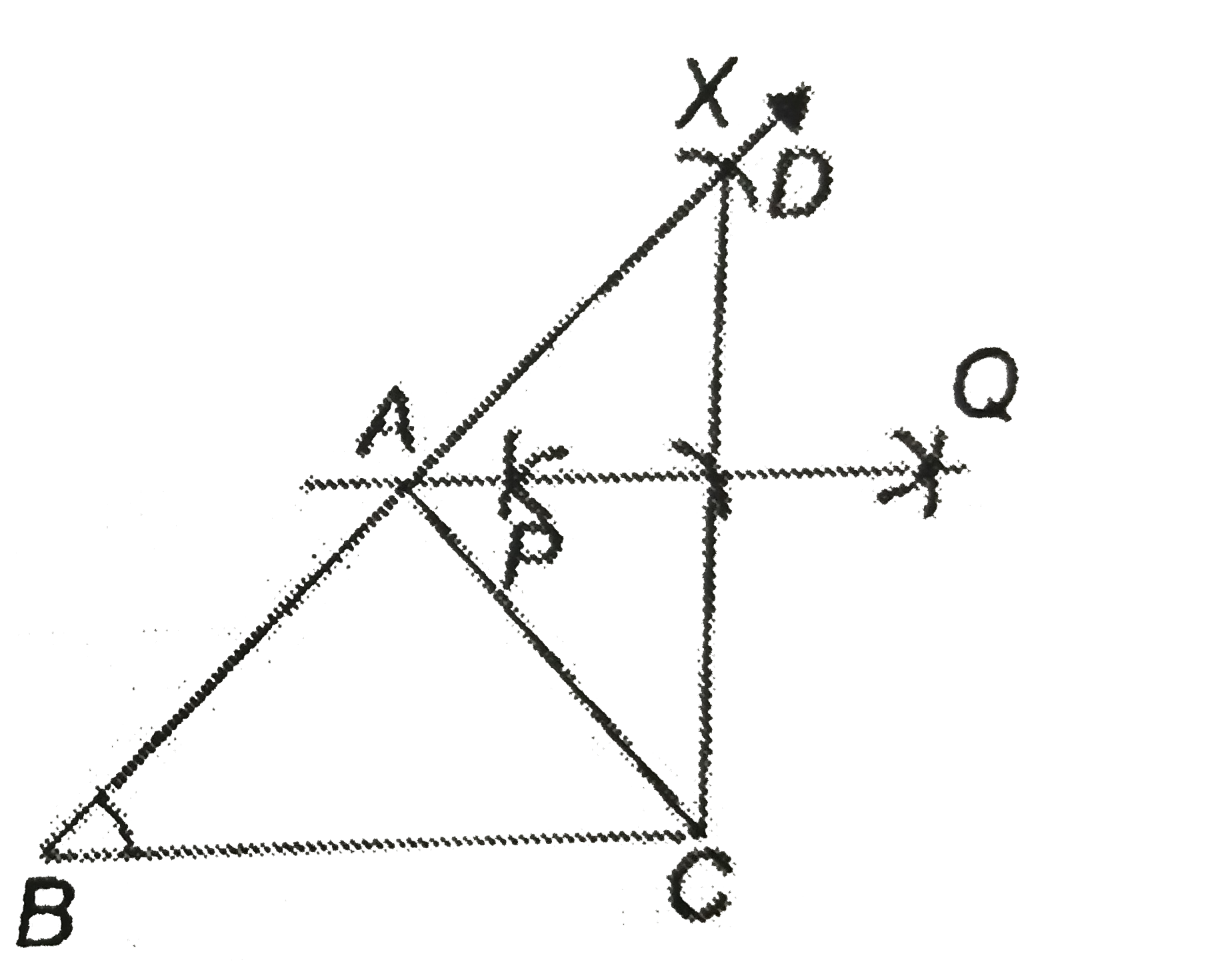
|
|
| 1498. |
In whichquadrantdoes the followingpoint lie ? |
|
Answer» |
|
| 1499. |
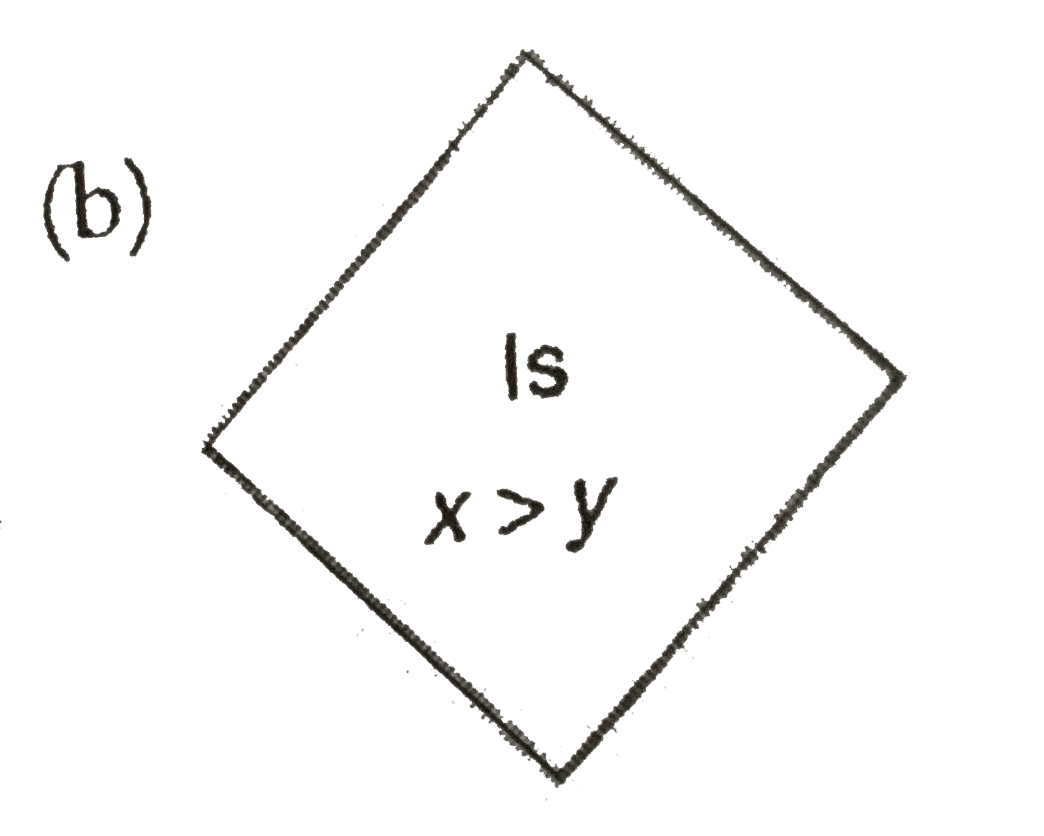
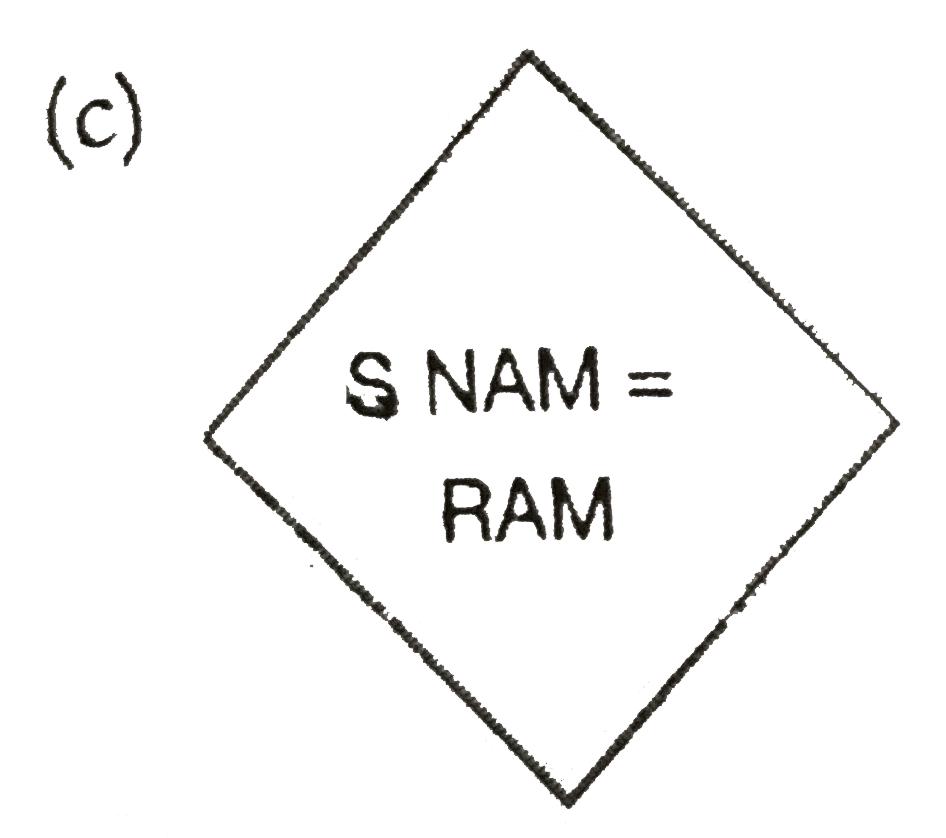
Which of the following is incorrect while writing flowchart? |
|
Answer»
|
|