Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 39901. |
Two point charges +8q and -2q located at x =0 and x=Lrespectively . The location of a point on the x-axis at which the net electric field due to these two point charges is zero is. |
| Answer» Answer :C | |
| 39902. |
Which series of the hydrogen spectrum lies in the visible region? |
| Answer» SOLUTION :BALMER SERIES | |
| 39903. |
A particle moves in the frame K with a velocity v at an angle theta to the x axis. Find the corresponding angle in the frame K^' moving with a velocity V relative to the frame K in the positive direction of its x axis, if the x and x^' axes of the two frames coincide. |
|
Answer» Solution :In the frame `K^'` the components of the velocity of the particle are `v_x^'=(vcostheta-V)/(1-(vVcostheta)/(c^2))` `v_y^'=(vsinthetasqrt(1-V^2//c^2))/(1-(vV)/(c^2)costheta)` HENCE, `TANTHETA^'=(v_y^')/(v_x^')=(vsintheta)/(vcostheta-V)SQRT((1-V^2)//c^2)` 
|
|
| 39904. |
Obtain an expression for the electric field intenstiy at a point on the equatorial line of an electric dipole. |
|
Answer» Solution : CONSIDER an electric dipole of dipole moment `P= qxx2a` placed in VACCUM. Whereq= magnitude of either charge 2a - distance between the charges Let p be the point on the equatorial line of the dipole at a distance r from the centre of the dipole O (fig ) Electric field at P DUE to the charge +q is `vecE_(1)= ((1)/(4piepsilon_(0)))(q)/((r^(2)+a^(2)))hatP` along Ap .... (1) Electric field at p due to the charge - q is `vecE_(2)((1)/(4piepsilon_(0)))(q)/((r^(2)+a^(2)))hatP` along PB.... (2)  Electric fileds `vecE_(1)` and `VecE_(2)` can be resolve into two rectangular components (Fig0 THe components `vecE_(1)` and `sintheta` and `vecE_(2)sintheta` are equal in magnitude but acting in opposite direction , so they cancel each other . The component `vecE_(1)costheta` and `vecE_(2)costheta` are acting parallel to the dipole axis gets at P is `vec = (E_(1)costheta + E_(2)costhat) hatp` `vecE= - 2E_(1)costhetahatP` `thereforeE_(1)=E_(2)` From equation (1) we get `vecE=-2[((1)/(4piepsilon_(0)))(q)/((r^(2)+a^(2)))]costhetahatP` `=-2 [((1)/(4piepsilon_(0)))(q)/((r^(2)+a^(2)))](a)/((r^(2)+a^(2))^(1//2))hatp` ` = - ((1)/(4piepsi_(0))) (2aq)/((r^(2) + a^(2))^(3//2))hatp` `vecE = - ((1)/(4piepsi_(0))) (p)/((r^(2) + a^(2))^(3//2))` If the dipole is short (i.e., a `lt lt` r) n`a^(2)` can be neglected. `vecE = - ((1)/(4piepsi_(0))) (p)/((r^(2))^(3//2)))` `vecE = - ((1)/(4piepsi_(0)))(p)/(r^(3))` |
|
| 39905. |
Intensity of point-like source at 1000 m is I. it is changed to 16I, then required distand will be |
|
Answer» 250 m `I=(phi)/(4 PI r^2)` `therefore I prop (1)/(r^2)` `therefore (I)/(I.)=((r.)/(r))^2` `therefore (I)/(16 I)=(r.^2)/((1000 m)^2)` `therefore r.^2=((1000 m)^2)/(16)` `therefore r.=(1000m)/(4)` `therefore r.=250` m |
|
| 39906. |
An electron travelling horizontally towards west enters into a magnetic field acting vertically down wards. It deflects towards |
|
Answer» South |
|
| 39907. |
An electric dipole is placed at an angle of30^(@)to a non-uniform electric field. The dipole will experience. |
|
Answer» A translational force only in the direction of the field. |
|
| 39908. |
A fixed thermally conducting cylinder has radius R and length L_0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P_0. While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is |
|
Answer» `((2P_(0) pi R^(2))/(pi R^(2) P_(0) + MG)) (2L` |
|
| 39909. |
What kind of p-n junction diode does not require any kind of bias? |
|
Answer» VECTOR diode |
|
| 39910. |
A capacitor consists of two stationaryplates shaped as a semi-circleof radius Radn a movableplate made of dielectricwith permittivity epsilon and capacble of rotoningaboutan axis O betweenthe stationary plates(fig). The thickness of the movables plateis equalto d which is practicallythe separationbetween teh stationaryplates. A potentialdifferenceV is appliedto the capacitor. FInd the magnitudeof the momentof forces relative to the axis O actingon teh movableplate in the position shown in the figure. |
|
Answer» Solution :When the capacitor is kept at a contant potential difference `V`, the WORK performed by the moment of electrostatic forces between the plates when the inner moveable plate is rotatedby an angel`d varphi` equals the increasesin the potential energy of the system. This comes about because when chagres are made, chagres flow from the battery to keep the potentialconstant and the AMOUNTOF the work done by these charges is twice it magnitudeand opposite in sign to the changein the energy of the capacitor Thus `N_(z) = (del U)/(del varphi) = (1)/(2) V^(2) (del C)/(del varphi)` Now the capacitor can be thought of as made up two parts (with and without the dielectric) in parallel. Thus `C = (epsilon R^(2) varphi)/(2d) + (epsilon_(0) epsilon (pi - varphi) R^(2))/(2d)` as the area of a sector of angle `varphi` is `(1)/(2) R^(2) varphi`. Defferenctian then gives `N_(s) = - ((epsilon - 1) epsilon_(0) R^(2) V^(2))/(4d)` The negative sign of `N_(x)` indicates that the moment of the force is acting clockwire (i.e., trying to SUCK in the-dielectric). |
|
| 39911. |
AB is part of a circuit as shown that absorbs energy at a rate of 50W. E is an emf device that has no internal resistance. |
|
Answer» Potential difference across AB is 48V. Resistance ABSORBS energy at the rate of 2 W. Potential difference across AB is VAB. I = 50W. `V_(AB) = 50V` Drop across RESISTOR is `2V`, THEREFORE emf of E is 48 V. As AB is absorbing energy at the rate of 50 W, 48W is being absorbed by E. Thus, E is on charging i.e., current is entering from positive terminal of E. |
|
| 39912. |
Beam expander Assume that a parallel beam is incident on two convex lens of focal length 20cm and 40cm. The beam has a diameter of 2cm. What should be the distance between them so that the final beam emerges parallel to the principal axis( Fig. 34-46) ? |
|
Answer» Solution :Here, again we can see that the image of one will act as an image of another. However , we can also see that for the FINAL beam to be parallel the object for it should be at its first focus. The image of first LENS is formed at its second focus. So, we can say that the distance between them should be equal to sum of their focal LENGTH. Calculation : From Fig. 34-46, it is clear that `d=f_(1)+f_(2)=60cm` Learning : If a parallel beam passes through a series of lens, under suitable arrangement, the width of the beam can be expanded. As can be seen from Fig. 34-46, the RADIUS of the beam is changed. This new radius can be found with the help of similar triangles. Here, we can say that `(R_(i))/(R_(f))=(f_(i))/(f_(f))` 
|
|
| 39913. |
A circular platform is mounted on a frictionless vertical axle. Its radius R=2 m and its moment of inertia about the axle is 200 kg m^2. It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 m s^(-1) relative to the ground. Time taken by the man to complete one revolution with respect to disc is |
|
Answer» `pi s` `L_i=0 , L_f= MVR-I omega`, so , `mvR = I omega` `omega=(mvR)/I=(50xx1xx2)/200=1/2` For ONE complete revolution, `(v+omegaR)t=2piR` `(1+1/2xx2)t=2pixx2 rArr t=2pi s`. |
|
| 39914. |
Obtain the answers (a) to (b) in Exercise if the circuit is connected to a high frequency supply ( 240 V, 10 kHz ) .Hence explain the statement that at very high frequency, an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a dc circuit after the steady state ? |
|
Answer» Solution :(a) From equation (1) of above answer, `I_(m) = ( ( 1.414 ) ( 110))/( sqrt(( 40)^(2) + ( 1)/( ( 4) (3.14 )^(2) ( 12000)^(2) ( 100 xx 10^(-6) )^(2))))` `:. I_(m) = 3.89 A `...(1) Now, in the ABSENCE of capacitor, `I_(m)^(.)= ( V_(m))/( R ) = ( sqrt( 2) V_(rms))/( R )` `:. I._(m) = (( 1.414) ( 110))/( ( 40))` `:. I._(m) = 3.8885A`...(2) `rArr` Equation (1) and ( 2)indicate that `I._(m) ~~ I_(m)` `rArr` At very high frequency of ac, capacitor acts like a simple conductor and hence the circuit becomes short circuit with minimum resistance. For dc supply, `f = 0 rarr X_(C ) = (1)/( 2 pi f C ) =oo` `rArr`Capacitor in a dc circuit will make it open circuit with infinite resistance ( after the steady STATE is reached ) . |
|
| 39915. |
Explain by drawing the energy levels of Si and Ge containing N atoms at 0 K temperature. |
|
Answer» Solution :Atomic number of Si is 14. The ELECTRON configuration of silicon atom is `1s^(2)2s^(2)2p^(6)3s^(2)3p^(2)`hence K and L shells are completely filled and M shell is incomplete and there are `3s^(2)3p^(2)` valence electron in it. And atomic number of Ge is 32. The electron configuration of silicon atom is `1s^(2)2s^(2)2p^(6)3s^(2)3p^(6)3d^(10)4s^(2)4p^(2)` hence K, L and M shells are completely filled and N shell is incomplete and there are `4s^(2)4p^(2)` valence electron in it. Hence both Si and Ge semiconductor are tetravalent. There are total 4 electrons in outermost orbit of Si or Ge crystal. The maximum possible number of electron in the outer orbit is `8(2s+6p` electrons). So, for the 4N valence electrons there are 8N energy states. These 8N discrete energy levels can either form a continuousband or they may be grouped in different BANDS depending upon the distance between the atoms in the crystal. At the distance between the atoms in the crystal lattices of Si and Ge, the energy band of these 8N states is split apart into two which are separated by an energy gap `E_(g)`, which is shown in the figure below.  The energy band positions in a semiconductor at 0 K. The upper band called the conduction band, consists of infinitely large number of closely spaced energy states. The lower band called the valence band, consists of closely spaced completely filled energy states. The lower band which is completely occupied by the 4N valence electrons at temperature of absolute zero is the valence band and there is an upper conduction ban with 4N energy levels, which is completely empty at absolutezero temperature. The lowest energy level in the conduction band is shown as `E_(c )` and highest energy level in the valence band is shown as `E_(v)`. Above `E_(c )` and below `E_(v )` there are a large number of closely spaced energy levels as shown in figure. The gap between the top of the valence band and bottom of the conduction band is called the energy band gap (Energy gap `E_(g)`). It is known as forbidden gap. |
|
| 39916. |
Give physical meaning of electric field. |
|
Answer» Solution :Electric field at a point in the space around a system of charges is the force on a unit positive test charge placed at that point without disturbing the system. Electric field is a characteristic of the system of charges and is independent of the test charge. Field is defined at every point in space and may vary from point to point. Electric field is a vector field, SINCE force is a vector quantity. The accelerated motion of charges produce electromagnetic waves which then propagate with the SPEED c. Thus, electric and magnetic fields can be detected by their effects (forces) on charges. FARADAY gave the IDEA of electric field |
|
| 39917. |
STATEMENT - 1 : If the velocity of centre of mass of a system is zero then the kinetic energy of the system may be greater than zero.and STATEMENT - 2 : Kinetic energy of the system is given by (1)/(2)int v^(2)dm, where dm is mass of element and v is its speed. |
|
Answer» STATEMENT - 1 is True, Statement - 2 is True, Statement - 2 is a correct EXPLANATION for Statement - 1. |
|
| 39918. |
A source contains two phosphorous radio nuclides ._(15)^(32)P (T_(1//2)=14.3d) and ._(15)^(33)P (T_(1//2)=25.3d). Initially, 10% of the decays come from ._(15)^(33)P. How long one must wait until 90% do so ? |
|
Answer» Solution :Suppose INITIALLY the source has 90% `._(15)Pt^(32)` and 10% `._(15)P_(1)^(32)`, say 9x gram of `P_(2)` and x gram of `P_(1)`. After t days, suppose the source has 90% `._(15)P_(2)^(33)` and `10 % ._(15)P_(t)^(32)` i.e., y gram of `P_(2)` and 9y gram of `P_(1)` we have to calculate : from `(N)/(N_(0))=((1)/(2))^(n)=((1)/(2))^(t//T)=2^(-i//T)` `N=N_(0)2^(-t//T)` `y=9x2^(-t//14.3` for `P_(2)` and `9y=x 2^(-t//25.3)` for `P_(1)` Dividing we GET `(1)/(9)=9xx2(t//25.3-t//14.3)` or `(1)/(81)=2^(-11 t//25.3)xx14.3` log 1 - log `81 = (-11 t)/(25.3xx14.3)` log 2 `0-1-9085=(-11 t)/(25.3xx14.3)xx0.3010`. `t=(25.3xx14.3xx1.9085)/(11xx0.3010)=208.5` days. |
|
| 39919. |
Calculate the average atomic mass of chlorine if no distinction is made between its different isotopes? |
|
Answer» Solution :The element chlorine is mixture of 75.77 % of `.."_(17)^(37) Cl` and 24.23 % of `""_(17)^(37) Cl` . So the AVERAGE atomic mass will be `(75.77)/(100) xx 34.96885u + (24.23)/(100) xx 36.96593 u= 35.453u` In fact , the chemist uses the averge atomic mass or SIMPLY CALLED chemical atomic weight (35.453 u for chlorine) of an element . So it must be eremebered that the atomic MAS whichs is MENTIONED in the periodic table is basically averaged atomic mass |
|
| 39920. |
find the tension T at time t developed in the loop as a result of induced current. |
| Answer» SOLUTION :`T=(B_(0)^(2)pir^(3))/(R)t` | |
| 39921. |
C-12 का 1/12 भार होता है |
|
Answer» 3 |
|
| 39922. |
What is the value of capacitive reactance (X_(C)) in DC circuits ? |
|
Answer» SOLUTION :As for DC circuits, V = 0 , therefore, ` X_(C) = (1)/(OMEGA C)` ` X_(C) = (1)/(2 PI vC) = infty ` |
|
| 39923. |
Early sunrise and delayed sunset is due to |
|
Answer» reflection |
|
| 39924. |
We have n identical light bubls, which draw a power P when connected across supply of 220V. If all of them is series are connected to 220V supply then power drawn is P_(1) and when all of them are connected in parallel them power drawn is P_(2), Find P_(2)//P_(1) |
|
Answer» Solution :Let R be the resistance of filament of a SINGLE BULB. USING `P= V^(2)//R`, we can write `P = (220)^(2)//R` …(i) When all of them are connected in series then equivalent resistance becomes nR, hence power drawn becomes `P_(1) = (220)^(2)//nR= P//n`. When all of them are connected in PARALLEL then the equivalent resistance becomes R/n. Hence, power drawn becomes `P_(2)= (220)^(2)//(R//n) = nP` Therefore, `P_(2)//P_(1) = n^(2)` |
|
| 39925. |
A stationary body of mass 3 kg explodes into three equal pieces. Two of the pieces fly off at right angles to each other, one with a velocity of 2 i m/s and the other with a velocity of 3 j m/s. If the explosion takes place in 10^(5)s, the average force acting on the third piece in newton is: |
|
Answer» `(3overset(WEDGE)(i)+3overset(wedge)(j))xx10^(-5)` `mvecupsilon=mxx2hati+mxx3hatj` `:.vecupsilon=2hati+3hatj` Now `veca=(vecupsilon)/(t)=(2hati+3hatj)/(10^(-5))` and`vecF=mveca=1xx(2hati+3hatj)xx10^(5)N` `=-(2hati+3hatj)xx10^(5)N`-ve SIGN because it is in OPPOSITE direction (b) is the choice 
|
|
| 39926. |
(i) If f = 0.5 m for a glass lens, what is the power of the lens? (ii) The radii of curvature of the faces of a double convex lens are 10 cm and 15 cm. Its focal length is 12 cm. What is the refractive index of glass? (iii) A convex lens has 20 cm focal length in air. What is focal length in water? (Refractive index of air-water = 1.33, refractive index for air-glass = 1.5.) |
|
Answer» Solution :(i) Power `= +2` dioptre. (ii) Here, we have `f = +12 cm, R1 = +10 cm, R2 = -15 cm`. Refractive index of air is taken as unity. We use the lens formula of Eq. (9.22). The sign CONVENTION has to be applied for `f, R_(1) and R_(2)` . Substituting the values, we have `(1)/(12)=(n-1)((1)/(10)-(1)/(-15))` This gives `n=1.5`. (iii) For a glass lens in air, `n_(2)=1.5, n_(1)=1, f=+20cm`. Hence, the lens formula gives `(1)/(20)=0.5[(1)/(R_(1))-(1)/(R_(2))]` For the same glass lens in water, `n_(2)=1.5, n_(1)=1.33`. Therefore, `(1.33)/(f)=(1.5-1.33)[(1)/(R_(1))-(1)/(R_(2))]` Combining these two EQUATIONS, we FIND `f=+78.2cm`. |
|
| 39927. |
What is the effect on the interference fringes in a Young' double slit experiment due to each of the following operations. a. the screen is moved away from the plane of the slits. b. the (monolchromatic) source is replaced by another (monochromatic) source of shorter wavelength. c. the separation between the two slits is increased. d. the source slit is moved closer to the double slit plane: e. the width of the source slit is increased. f. The monochromaticsource is replaced by a source of white light? (in each operation, take all parameters, other than the one specified, to remain unchanged). |
|
Answer» Solution :a. Angular separation of the fringes remains constant `(=(lamda)/d)`. The actual separation of the fringes increases in proportion to the distance of the screen from the plane of the two slits. b. The separation of the fringes (and also angular separation) decreases. See the condition mentionedin (d) below . c. The separation of the fringes ( and also angular separation) decreases. See, the condition mentioned in d. below. d. Let s be the size of the source and S its distance from the plane of the two slits.For interference fringes to be seen,the conditioin `s/Slt(lamda)/d` should be satisfied,otherwise, interference PATTERNS produced by DIFFERENT parts of the source overlap and no fringes are seen. Thus,as S decreases(i.e.the source slit is brought closer), theinterference pattern gets less and less sharp, and when the source is brought too close for this condition to be valid, the fringes disappear. Till this happens, the fringe separation remains fixed. e.Same as in d.As the source slit width increases,fringe pattern gets less and less sharp. When the source slit is so wide that the condition`s/Slt(lamda)/d` is not satisfied, the interference pattern disappears. f.The interference patterns due to different component COLOURS of white light overlap (incoherently). The central bright fringes for different colours are the same position. Therefore, the central fringe is white. For a point P for which `S_(2)P-S_(1)P=(lamda_(b))/2` where `lamda_(b) (~~4000Å)` represents the wavelength for the blue colour, the blue component will be absent and the fringe will appear red in colour. Slightly farther away where `S_(2)Q-S_(1)Q=lamda_(b)=(lamda_(r))/2` where`lamda_(r)(~~8000Å)` is the wavelength for the red colour, the fringe will be predominantly blue. Thus, the fringe closest on EITHER SIDE of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen. |
|
| 39928. |
Assertion : Most amplifiers use common emitter circuit configuration. Reason : Its input resistance iscomparatively higher. |
|
Answer» If both ASSERTION and reason are true and reason is the correct explanation of assertion |
|
| 39929. |
Match the corresponding entries of column-1 with column-2. (Where m is the magnification produced by the mirror.) |
|
Answer» (1 - a and C), (2 – a and d), (3 – a and B) (4 – c and d) |
|
| 39930. |
Define work function of a metal. Give its unit. |
| Answer» Solution :The MINIMUM energy NEEDED for an ELECTRON to escape from the metal SURFACE is called work function of that metal. It.s UNIT is electron volt (eV). | |
| 39931. |
Answer the following questions: (d) Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease? |
| Answer» SOLUTION :(d) The APPARENT DEPTH for oblique viewing decreases from its value for near-normal viewing. Convince yourself of this fact by drawing ray diagrams for DIFFERENT positions of the observer. | |
| 39932. |
Obtain the equaitons for constructive and destructive interference for transmitted and reflected waves in thin films. Interference in thin films: |
Answer» Solution :Let us consider a thin film oftransparent material of REFRACTIVE index `mu` (not to consuse with order of fringe n) and thickness d. A parallel bema of light is incident on the film at an angle i. The wave is divided into two parts at the upper surface, one is reflected and the other is refracted. The refracted part, which enters into the film, again gets divided at the lower surface into two parts, one is transmitted out of thefilm and the other is reflected back in to the film. Reflected as well asrefracted waves are sent by the film as multiple reflectins take place inside the film. The interference is produced by both the reflected and transmitted light.  For transmitted light: The light transmitted may INTERFERE to produe a reslultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where spliting occured. The extra path travelled by the wave transmited from D is the path inside the film, BC + CD. If we approximate the incidence to be nearly normal (i = 0), then the POINTS B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is travesed in a medium of refractive index `mu`, the optical path difference is `delta = 2MU d`. Similarly, the condition for destructive interference in transmitted ray is, `2mu d = (2n - 1) (lambda)/(2)` For reflected light: It is experimentally and theoretically proved that a wave while travelling in a rarer medium and getting relfected by a dener medium, undergoes a phase change of `pi`. Hence, an additional path difference of `lambda//2` should be considered. Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film. The additional path travelled by were coming out fromC is the path inside the film, AB + BC. For nearly normal incidence this refractive index `mu` the optical path difference is, `delta = 2mu d`. The condition for `2mud+(lambda)/(2)=nlambda(or)2mud=(2n-1)(lambda)/(2)` The additional path difference `lambda//2` is due to the phase change of `pi` in rarer to denser reflection taking place at A. The condition for destructive interference for reflected rays is, `2mud+(lambda)/(2)=(2n+1)(or)2mud=nlamda.` |
|
| 39933. |
Given below are some famous numbers associated with electromagnetic radiations in different contexts in physics. State the part of the electromagnetic spectrum to which each belongs. (a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space). (b) 1057 MHz (frequency of radiation arising from two close energy levels in hydrogen, known as Lamb shift). (c) 2.7 K [temperature associated with the isotropic radiation filling all space-thought to be a relic of the ‘big-bang’ origin of the universe]. (d) 5890 Å - 5896 Å [double lines of sodium] (e) 14.4 keV [energy of a particular transition in ""^(57)Fe nucleus associated with a famous high resolution spectroscopic method (Mössbauer spectroscopy)]. |
|
Answer» SOLUTION :(a) Radio (short wavelength end) (b) Radio (short wavelength end) (C) Microwave (d) VISIBLE (Yellow) (E) X-rays (or soft `lamda`-rays) REGION |
|
| 39934. |
If in the infinete series circuit C = 9muF and C_(1) = 6muFthen the capacity across AB is in ........ muF |
|
Answer» `3muF` |
|
| 39935. |
Which value of current do you measure with an A.C ammeter? |
| Answer» SOLUTION :RMS VALUE of CURRENT | |
| 39936. |
Rank the electrostatic potential energies for the given system of charges in increasing order ……….. . |
|
Answer» `1=4 lt 2 lt 3` |
|
| 39937. |
In Newton.s corpuscular theory, no attempt was made to explain |
|
Answer» the DIFFERENT COLOURS of light |
|
| 39938. |
When a wave undergoes reflection at a denser medium, what happens to its phase? |
| Answer» SOLUTION :When a undergoes a REFLECTION at a denser medium then it.s crest reflected as through and VICE versa So, its PHASE changes at `180^(@)`. | |
| 39939. |
A solenoid a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 2A. If the number of turns is 1000 per metre, calculate (a) H, (b) B and (c) the magnetising current I_m. |
|
Answer» Solution : a. The field H is dependent of the material of the core, and is `H=nI=1000xx2.0=2xx10^(3)A//m` b. The magnetic field B is given by, `B=mu,mu_0H=400xx4pixx10^(-7)(N//A^2)xx2xx10^3(A//m)=1.0T` c. MAGNETISATION is given by, `M=((B-mu_0H))/(mu_0)=(mu_rmu_0H-mu_0H)/(mu_0)=(mu_r-1)=399xxH` d. The magnetising current `I_M` is the ADDITIONAL current that needs to be passed through the windings of the solenoid in the ABSENCE of the core which would give a B value as in the presence of the core . Thus, `B=mu_(r)n_(0)(I+I_(M))`. USING I = 2A , b = 1T , we get `I_M=794A`. |
|
| 39940. |
How can you measure a high current using a galvanometer? |
| Answer» Solution :The GALVANOMETER can be converted by connecting a SHUNT (or LOW) resistance across its TERMINALS. | |
| 39941. |
A coil of inductance 0.50 H and resistance 100 ohm is connected to 240 V, 50Hz ac supply. What is the peak current in the coil? b) What is the time lag between the peak voltage and the peak current? |
|
Answer» Solution :Here `L=0.50H, R=100ohm` `E_("rms")=240V, v=50Hz` STEP 1. We know `E_(0)=sqrt2E_("rms")=1.414xx240=339.4V` `"Impendance of LR circuit is"` `Z_(L)=sqrt(R^(2)+omega^(2)L^(2))=sqrt(R^(2)+4piv^(2)L^(2))` `sqrt((100)^(2)+4xx(3.14)^(2)xx(50)^(2)xx(0.50)^(2))="186.1 ohm"` `"PEAK CURRENT, "I_(0)=(E_(0))/(Z_(L))=(339.4)/(186.1)=1.82A` In LR circuit the phase difference between current and voltage `phi` which is given by `tan phi=(Lomega)/(R)=(Lxx2piv)/(R)` `tan phi=(0.50xx2xx3.14xx50)/(100)=1.57` `phi=tan^(-1)(1.57)=57^(0)30^(1)=57.5^(0)` `=(57.5xxpi)/(180)=0.3194 pi" radians"` `therefore "Time lag between "E_(0) and I_(0)" is given by"` `t=(phi)/(omega)=(phi)/(2piv)=(0.319pi)/(2pixx50)` `=0.003194s=3.194xx10^(-3)`s`. |
|
| 39942. |
A gamma ray photon of energy 1896 MeV annihilates to produce a proton-antiproton pair. If the rest mass of each of the particles involved be 1.007276 a.m.u approximately, find how much K. E these will carry? |
|
Answer» Solution :WORKING on the same lines as an electron - positron pair production ,we notice that the reaction. `GAMMA rarr` proton + antiproton + antiproton , has the energy balance `E=m_(0("proton"))C^2+K.E._(("proton"))+m_(0("antiproton"))C^2K.E_(("antiproton"))` But `m_(0)C^2`= energy equivalent of 1.007276 a.m.u `~~` 938 MEV. `[ :. 1.007276xx931~~938"MeV"]` THUS K.E of each particle `=1/2` [ 1896 MeV `-2xx938` MeV] = 10 MeV |
|
| 39943. |
Find the equivalent capacitance between A and B (a) (b) . |
Answer» Solution :(a) By Kirchoff's rules (same procedure as in FINDING equivalent resistance) 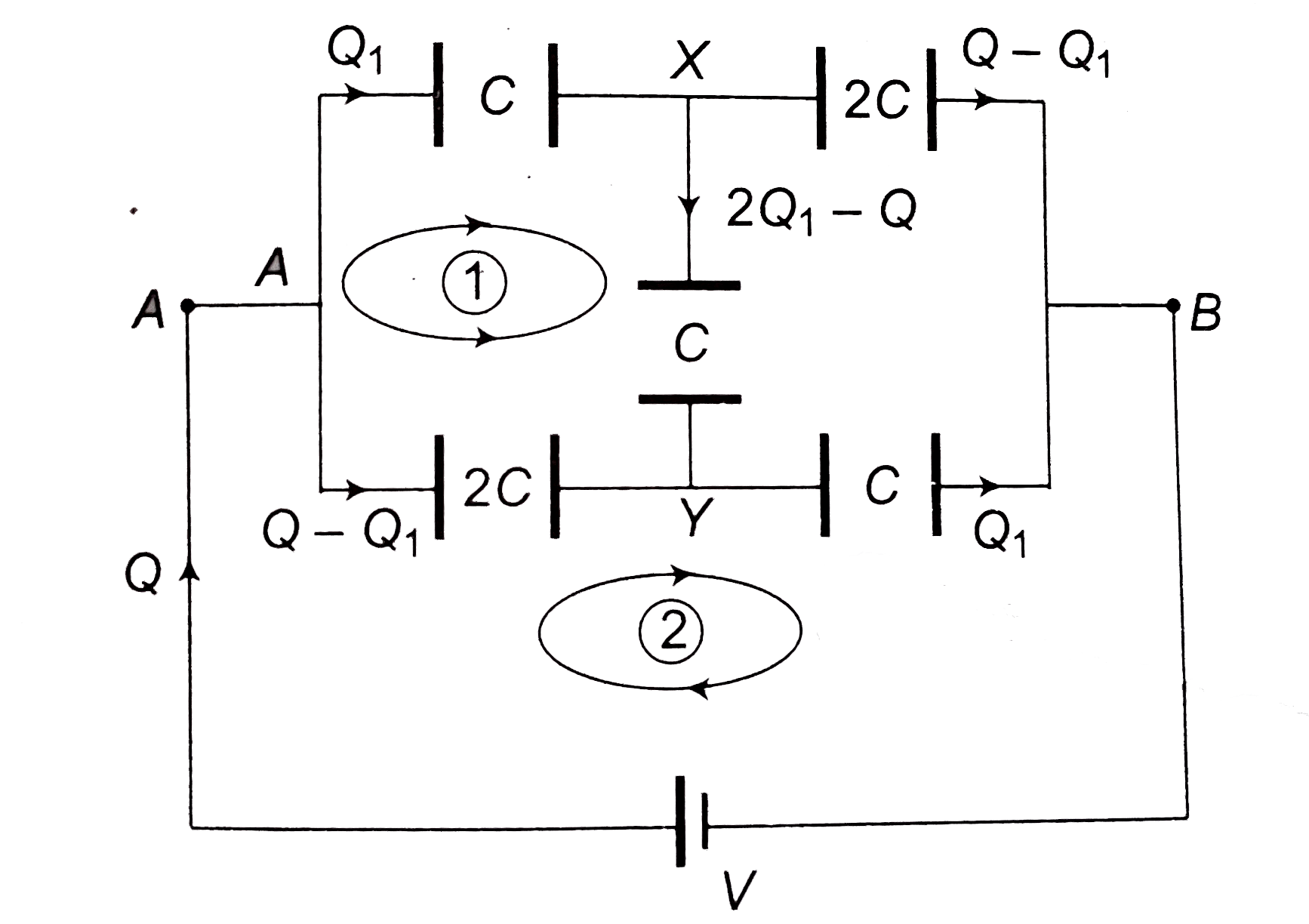 `Lo op ①, A to A , path AXYA` `V_A -(Q_1)/(C) -(2 Q_1 -Q)/(C) +(Q -Q_1)/(2C) = V_A` `-2 Q_1 - 4 Q_1 + 2Q + Q - Q_1 = 0` `7 Q_1 = 3 Q rArr Q_1 = 3 Q//7` `Lo op ②, A to A, path AYBA` `V_A -(Q -Q_1)/(2C) -(Q_1)/(C)+ V = V_A` `(Q -Q_1)/(2 C) + (Q_1)/(C) = V` `(Q_ + Q_1)/(2 C) = (Q + 3 Q//7)/(2 C) = V` `(10 Q)/(14 C) = V rArr (Q)/(V) = (14 C)/(10) = (7C)/(5)` `C_(eq) = (7 C)/(5)` Alternately by Delta-start method :  Replace Delta `APQ` by a star `X = C + 2C + (C . 2C)/(C) = 5 C` `y = C + C + (C.C)/(2 C) = (5 C)/(2)` `z = C + 2C + (C.2C)/(C) = 5 C` 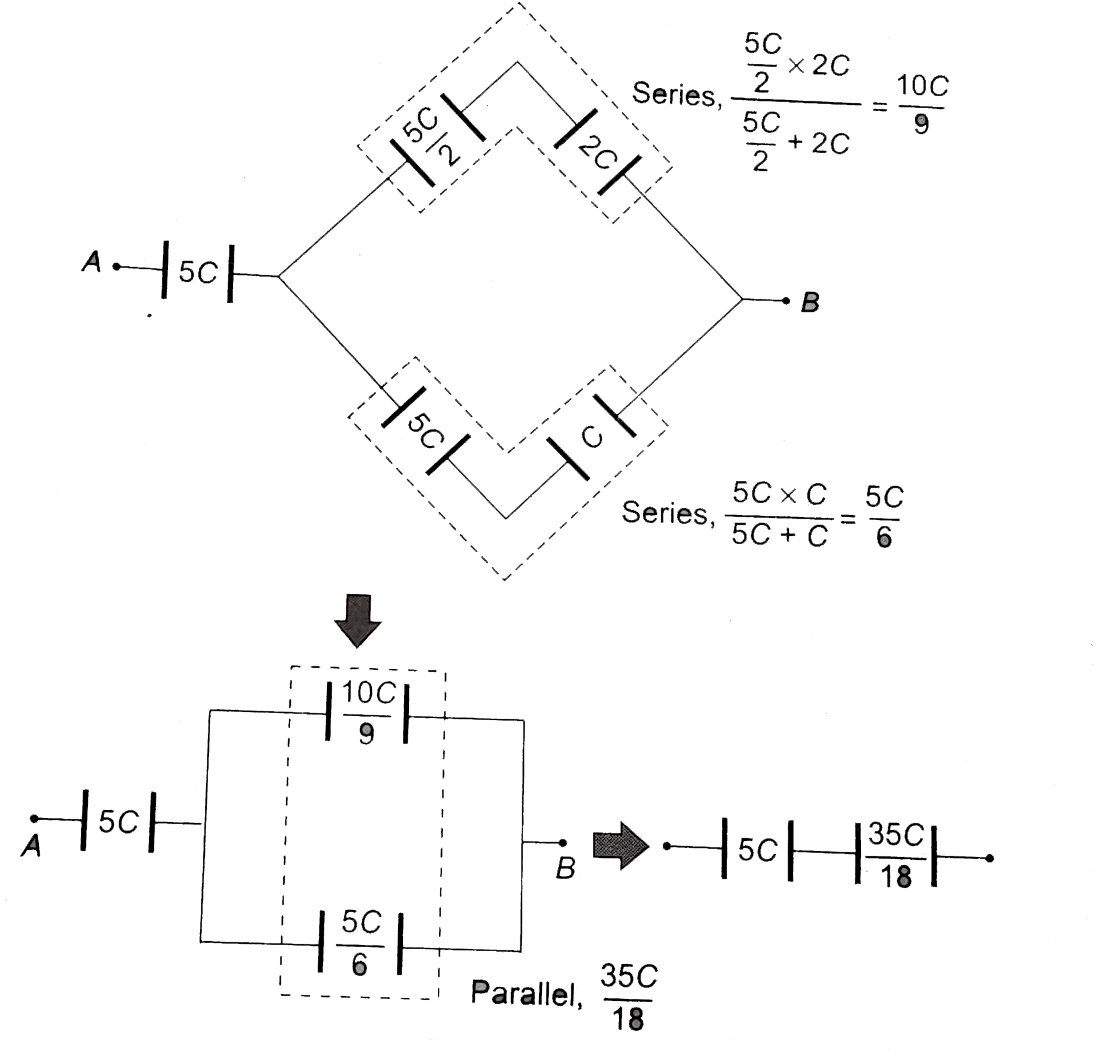 `C_(eq) = (5 C xx (35 C)/(18) )/(5C + (35)/(18)) = (7 C)/(5)` (b)  By symmetry, branches `AXB` and `PXQ` are not CONNECTED. MAKE branch `AXB` as shown. 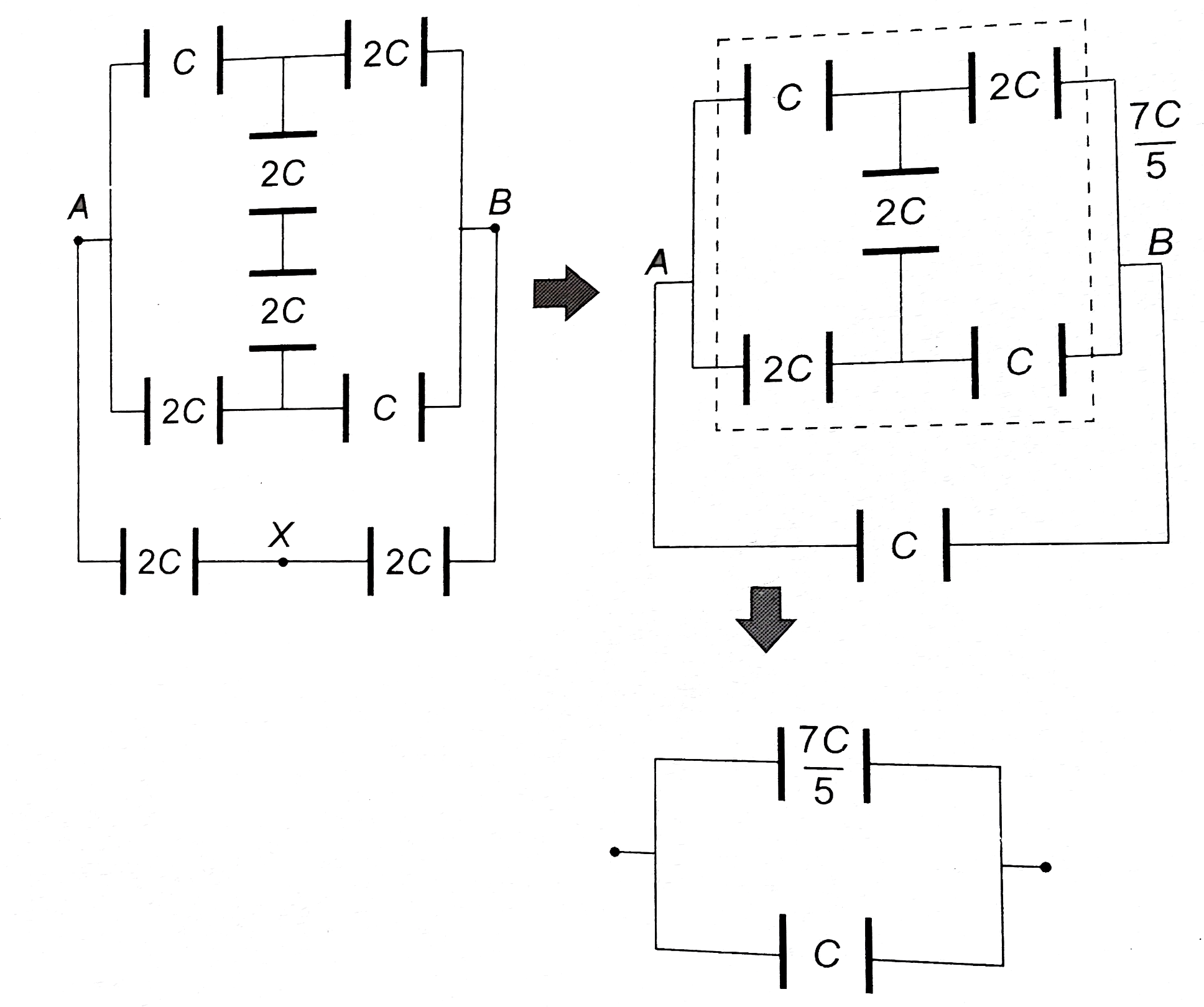 `C_(eq) = (7 C)/(5) + C = (12 C)/(5)`. |
|
| 39944. |
Consider N identical capacitors, each of capacitance 'C'. What is the ratio of maximum capacitance to minimum capacitance using all of them ? |
|
Answer» Solution :When all of them are connected in PARELLEL, the maximum CAPACITANCE is CN.When all of them are connected in SERIES, the minimum capacitance is `C/N`. Then RATIO, maximum capacitance/minimum capacitance=`(CN)/(C/N)=N^2` |
|
| 39945. |
Answer the following questions: A hot piece of iron is immersed in cold water. Has the internal energy of water increased ? Has any work been done by the iron? |
| Answer» Solution :YES, it is increased, the increase is due to transfer of HEAT and not due to any work. | |
| 39946. |
Set the following vectors in the increasing order of their magnitude. (a) 3hati+4hatj ""(b)2hati+4hatj+6hatk (c) 2hati+2hatj+2hatk |
| Answer» Answer :B | |
| 39947. |
Magnetic Induction B at a point well inside the solenoid is B = _____ |
| Answer» SOLUTION :`mu_0` N I | |
| 39948. |
What vector represents at any point in a measure of rate of flow of energy as stated by poynting theorm per unit area at that point ? |
| Answer» SOLUTION :1/mu_0(VECEXXVECB) | |
| 39949. |
Did Margie like her current classroom, teacher,and education? |
|
Answer» Yes |
|
| 39950. |
Three equal charges +q are placed at the three vertices of an equilateral triangle centered at the origin.They are held in equilibrium by a restoring force of magnitude F(r) = kr directed towards the origin, where k is a constant.What is the distance of the three charges from the origin ? |
|
Answer» `[(1)/(6piepsilon_(0))(Q^(2))/(K)]^(1//2)` |
|