Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 45351. |
When NaCl molecule is formed, one electron is transferred from Na atom to CI atom. The equilibrium internuclear distance between Na+ and Cl^(-)ions is 2.75 xx 10^(-10)m. The dipole moment of NaCl molecule is |
|
Answer» `2.75 XX 10^(-19)` cm `=1.6 xx 10^(19) xx 2.75 xx 10^(-10)` `=4.4 xx 10^(-29)` cm |
|
| 45352. |
Prove that the field on the surface of a sphere carrying a uniformly distributed electric charge is equal to that which would have been established, if the entire charge were concentrated in the centre of the sphere. |
|
Answer» Solution :Construct a second sphere AROUND the sphere under consideration and suppose it carries a charge EQUAL in magnitude, but opposite in sign (Fig. 24.14). According to the result OBTAINED in the PREVIOUS problem, the charge of the outer sphere does not create a field inside it. Therefore the field between the spheres is created only by the charge of the internal sphere. If there is LITTLE difference between the radii of these spheres (i.c. if `R_(1)-R lt lt R)` , the field in between will be almost homogeneous, and its strength will be (see 37.5) `E=(sigma)/(epsi_(0))=(Q)/(epsi_(0)S)=(Q)/(4pi epsi_(0)R^(2))` |
|
| 45353. |
A conductor ABCDE has the shape shown. It lies i the yz plane, with A and E on the y-axis . When it moves with a velocity v in a magnetic field B, an emf e is induced between A and E |
|
Answer» `e=0` if `V` is in the `y`-direction and `B` is in the `x`-direction. |
|
| 45354. |
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25cm), and (b) at infinity? What is the magnifying power of the microscope in each case ? |
|
Answer» Solution :`f_(0) cm , f_(e)= 6.25` cm Distance between object lens and eyepiece = 15 cm `therefore (1)/(v_(e)) - (1)/(u_(e)) = (1)/(f_(e))` - `(1)/(u_(e)) = (1)/(f_(e)) - (1)/(v_(e)) = (1)/(6.25) - (1)/((-25)) = (1)/(5) cm "" therefore u_(e) =- 5 ` cm Object is on the left of object lens. Distance of the image from the objective lens = 15 -5 = 10 cm i.e., `v_(0) = 10` cm `(1)/(v_(0)) - (1)/(u_(0)) = (1)/(f_(0)) "" - (1)/(u_(0)) = (1)/(f_(0)) - (1)/(v_(0)) = (1)/(2) - (1)/(10) = (5 - 1)/(10) = (4)/(10)` `u_(0) = -2.5` cm Magnifying power = M = `(v_(0))/(-u_(0)) [ 1 + (D)/(f_(e)) ]= (10)/(+ 2.5) [ 1 + (25)/(6.25) ] ` = 20 B. When final image is at INFINITY , then object must be placed at the focus of the eyepiece. `u_(e)= - f_(e)= - 6.25 ` cm `v_(0) = L - |u_(e)| = 15 - 6.25 = 8.75 ` cm `(1)/(v_(0)) - (1)/(u_(0)) = (1)/(f_(0)) "" - (1)/(u_(0)) = (1)/(f_(0))- (1)/(v_(0)) = (1)/(2) - (1)/(8.75) = (8.75 - 2)/(8.75 xx 2) = (6.75)/(15.50)` `u_(e) = - 2.6 ` cm M = `((-v_(0))/(v_(0))) . (D)/(f_(e)) = (8,75)/(2.6) xx (25)/(6.25) = 13.5` |
|
| 45355. |
A one metre steel wire of negligible mass and area of cross-section 0.01 cm^(-2) is kept on a smooth horizontal table with one end fixed.A ball of mass 1 kg is attached to the other end. The ball and the wire are rotating with an angular velocity of omega. If the elongation of the wire is 2 mm, then omega is (Young's modulus of steel = 2 xx 10^(11) Nm^(-2) ) |
|
Answer» 5 rad `s^(-1)` = `2 xx 10^(-3)` m Mass of the ball, m=1 kg Length of wire, l = 1 m area of cross - sectional of wire, A= 0.01`cm^(2) = 0.01 xx 10^(-4)` m Young.s modulus of steel, R = `2 xx 10^(11) Nm^(-2)` `therefore` TENSION force in wire , T = m `OMEGA^(2)`l `therefore ` Stress = `("Tension")/("Area") = (m omega^(2)l)/(A )` Strain = `( Delta l)/(l ) = ("stress")/("Young.s modulus")` ` Delta l=(m omega^(2) l^(2))/(YA)` or`omega = sqrt((YA Delta)/(ML^(2))` putting the given values, we get `=sqrt((2 x 10^(11) xx 0.01 xx 10^(-4) xx 2 xx 10^(-3))/(1 xx (1)^2))` `omega = 20 rad/"sec"^(-1)` |
|
| 45356. |
The magnetic field at the center of a current carrying loop of radius 0.1 m is 5sqrt( 5) times that at a point along its axis. The distance of this point from the centre of the loop is |
|
Answer» 0.2 m `(B_("centre"))/(B_("axis"))=(1+(x^(2))/(r2))^(3//2)` Given that, `B_("centre")=5sqrt(5)B_("axis")` `(B_("centre"))/(B_("axis"))=5sqrt(5)` `therefore 5sqrt(5)=[1+(x^(2))/((0.1)^(2))]^(3//2)` On squaring both sides, we get `25xx5 = [1+(x^(2))/((0.1)^(2))]` `root(3)(125)=1+(x^(2))/((0.1)^(2))` `RARR 0.01 + x^(2)=0.05` `rArr x^(2)=0.005 - 0.01` `rArr x^(2)=0.04` `rArr x = 0.2 m` |
|
| 45357. |
When a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s) |
|
Answer» 33.3 HZ |
|
| 45358. |
A thin prism of crown glass (m_r=1.515, m_v=1.525)and a thin prism of flint glass (mu_r=1.612, mu_v=1.632) are placed in contact with each other. Their refracting angles are 5.0^@ each and are similarly directed. Calculate the angular dispersion produced by the combination. |
|
Answer» |
|
| 45359. |
A long round conductor of cross- sectional area S is made of material whose resistivity depends only on distance r from the axis of the conductor as rho = (alpha)/(r^2) , where alpha is a constant. Find (a) the resistance per unit length of such a conductor. (b) the electric field strength in the conductor due to which a current i flows through it . |
Answer» Solution :Consider a CYLINDRICAL element of radii between r and (r+ DR) . Its resistance  `dR = (rhol)/(2pi dr) ` (or)` 1/(dR) = (2pi r dr)/(rhol)""……(i)` `THEREFORE 1/R = int_0^a 1/(dR) = int_0^a (2pi)/(rhol)r dr` (where a is the radius of the conductor ) `int_0^a (2pir dr)/(((alpha)/(r^2))l) = (2pi)/(alphal) int_0^a r^3 dr = (2pi)/(alpha l) ((a^4)/(4)) = ((pia^2)^2)/(2pialphal) = (S^2)/(2pi alpha l)` `R = (2pi alpha l)/(S^2) "".....(ii)` The resistance per unit length of wire `R= (2pi alpha)/(S^2)` (b) Equation (ii) can be written as `R= ((2pialpha)/(S)) ((l)/(S))` COMPARE with `R = (rhol)/(S) , ` we get `rho = (2pi alpha)/(S)` By Ohm.s law `E= jrho = i/S xx (2pi alpha)/(S) = (2pi alpha i)/(S^2)` |
|
| 45360. |
Radius of the nucleus of the atom with A=216 is (R_0 =1.3fm) |
|
Answer» 7.2 fm |
|
| 45361. |
(A): When a battery is short-circuited the terminal voltage is zero (R): In the situation of short circuit, current is zero |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the correct explanation of 'A' |
|
| 45362. |
An oil droplet of 0.01 mm diameter floats in equilibrium between two horizontal plates the distance between which is 25 mm. What is the charge of the droplet, if the equilibrium corresponds to a voltage of 3.6 xx 10^(4)V across the plates? |
Answer» Solution :A force of gravity directed DOWNWARDS and equal to `mig=4//6pi D^(8)rhog`ACTS on the DROPLET. It is countorboloncod by on blootrio force `F=qE=q varphi//d` (FIG. 24.4). The charge of the droplet is found from the balance of forces. 
|
|
| 45363. |
The current in a coil changes from +10A to -2A in 3 millisecond. hat is the induced e.m.f. in the coil ? The self-inductance of the coil is 2 mH. |
|
Answer» 8V |
|
| 45364. |
State de-Broglie hypothesis. |
| Answer» SOLUTION :De-Broglie hypothesis STATES that atomic particles of matter moving with a GIVEN VELOCITY, (or momentum) can display wave like properties. | |
| 45365. |
The kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is - |
|
Answer» zero |
|
| 45366. |
Calculate the ratio of electric and gravitational force between two protons. Charge of each proton is 1.6 xx 10^(-19)C,mass is 1.672 xx 10^(-27) kg and G = 6.67 xx 10^(-11) Nm^(-2)kg^(-2)? |
|
Answer» SOLUTION :`Q_1 = 1.6 xx 10^(-19) C, Q_2 = 1.6 xx 10^(-19) C` r is the distance between the two protons ELECTROSTATIC force between two protons `F_1 = 9 xx 10^(9) (Q_1Q_2)/(r^2) m_1 = m_2 = 1.672 xx 10^(-27) kg` `G = 6.67 xx 10^(-11) NM^(2)//kg^(2)` Gravitational force between them `F_2 = G(m_1 m_2)/(r^2) :. (F_1)/(F_2) = (9 xx 10^9 Q_1Q_2)/(G.m_1 m_2)` `= (9 xx 10^(9) xx 1.6 xx 10^(-19) xx 1.6 xx 10^(-19))/(6.67 xx 10^(-11) xx 1.672 xx 10^(-27) xx 1.672 xx 10^(-27)) = 1.23 xx 10^(36)` |
|
| 45367. |
The magnetic field of earth can be modelled by that of a pointplaced at the centre of the earth the dipole axis makesan angle of 11.3^(@)with the axis ofearth at mumbaideclination is nearly zero then |
|
Answer» the declination variis between `11.3^(@)` w to `11.3^(@)` e |
|
| 45368. |
A monochromatic light source is placed at a distance d from a metal surface. Photo electrons are ejected at a rate n, kinetic energy is being E. If the source is brought nearer to distance d/2, the rate and kinetic energy of emitted photo electrons becomes nearly |
|
Answer» 2N and 2E |
|
| 45369. |
In Young's double slit experimentt. When a glass plate (mu = 1.5) of thickness is introduce path of one of the interfering beams (wavelength = lambda) the intensity at the position where centre maxima occurred previous remains unchanged. The minimum thickness |
|
Answer» `2 LAMBDA` |
|
| 45370. |
The ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person. A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm. A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina. The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100//3cm ), then number of lens will be +3. For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens. Q. A personcan see objects clearly fromdistance 10cm to oo. Then, we can say that the person is |
|
Answer» normal sighted PERSON |
|
| 45371. |
Solve a similar problem for the case of a tungsten ball. The magnetic susceptibility of tungsten is chi_(m)=1.76 xx 10^(-4). |
|
Answer» |
|
| 45372. |
The wavelength of de-Broglie wave associated with a thermal neutron of mass m kg at 27^⋅C is (KB is the Boltzmann constant and all quantities are in SI units) |
|
Answer» `H/(sqrt100mK_B) METRE` |
|
| 45373. |
A concave lens always produces _____ images. |
|
Answer» real |
|
| 45374. |
A ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium A is .... |
|
Answer» `sin^(-1)((16)/(15))` `n_(AB)=(n_A)/(n_B)` `SINC=(1)/(n_(AB))=(n_B)/(n_A)` `THEREFORE C=sin^(-1)((n_B)/(n_A))` `=sin^(-1)((1.5)/(1.6))=sin^(-1)((15)/(16))` |
|
| 45375. |
Draw a diagram of an illuminated p-n junction solar cell. |
| Answer» SOLUTION :The diagram of an illuminated p-n JUNCTION SOLAR cell is GIVEN in. | |
| 45376. |
Nuclear binding energy is equivalent to |
|
Answer» MASS of proton |
|
| 45377. |
Assertion:Isotopes of an element can be separated by using a mass spectrometer. Reason: Separation of isotopes is possible because of difference in electronnumber of isotopes . |
|
Answer» If both assertion and reason are true and reason is the correct explanation of assertion . |
|
| 45378. |
Explain the determination of the internal resistance of a cell using voltmeter. |
Answer» Solution :Determination of internal RESISTANCE: The emf of cell `xi` is measured by connecting a high resistance voltmeter across it without connecting the external resistance R. Since the voltmeter draws verylittle current for DEFLECTION, the circuit may be considered as open. Hence, the voltmeter READING gives the emf of the cell. Then external resistance R is included in the circuit and current I is extablished in the circuit. The potential differenceacross R is equal to the potential difference across the cell (V).  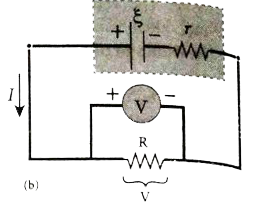 The potential drop across the resistor R is `V=IR "" ...(1)` Due to internal resistance r of the cell, the voltmeter reads a value V, which is less than the emf of cell `xi`. It is because, CERTAIN amount of voltage (Ir) has dropped across the internal resistance r. Then`V=xi-Ir` `Ir=xi-V "" ...(2)` DIVIDING equation (2) by equation (1), we get `(Ir)/(IR)=(xi-V)/(V)` `r=|(xi-V)/(V)|R"" ...(3)` Since `xi, V and R` are known, internal resistance r can be determined. |
|