Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

45301.

An ammeter and a voltmeter of resistance R are connected in series to a cell of negligible internal resistance. Their readings are A and V respectively. If an other resistance R is connected in parallel with the voltmeter

Answer»

Both A and V increases
Both A and V DECREASES
A decreases but B increases
A INCREASE but V decreases

Answer :D
Discussion
45302.

A substance is dipped in liquid, then due to which reason, substances will be invisible ?

Answer»

When SUBSTANCE REACTS as perfect reflector.
When it absorbs the LIGHT completely.
When its refractive index is 1.
When refractive indices of substance and liquid are same.

Solution :When both have same refractive indiccs, then SURFACE doesn.t reflect or refract, hence it will be visible.
Discussion
45303.

In a series LCR circuit R = 10 Omega and the impedance Z = 20 Omega. Then the phase difference between the current and the voltage is

Answer»

`60^(@)`
`30^(@)`
`45^(@)`
`90^(@)`

ANSWER :A
Discussion
45304.

If a current of 3A, flowing in the primary coil is reduced to zero in 10^-3s, the induced e.m.f. in the secondary coil is 15000V. The mutual inductance between the two coils is?

Answer»

SOLUTION :`e_s = M(dI_p)/DT`
`THEREFORE 15000 = Mxx3xx10^3`
`therefore M = 5H`
Discussion
45305.

What do you mean by terms 'in phase' ?

Answer»

Solution :Let `I_1` and `I_2` be the INTENSITIES of TWO BEAMS having AMPLITUDES `a_1` and `a_2.`
`I_1/I_2=9/1`
But,`I_1/I_2=a_1^2/a_2^2 `
` therefore a^2_1/a_2^2=9/1` or, `a_1/a_2=3/1`
If `a_max` and `a_min` are the amplitudes are maxima and MINIMA.
`a_max/a_min =a_1+a_2/a_1-a_2=3+1/3-1=4/2=2/1`
`I_max/I_min=a^2_max/a^2_min=4/1`
Discussion
45306.

Figure shown plane waves refracted for air to water using Huygen.s principle a,b,c,d ,e are lengths on the diagram . The ratio of refractive index of water w.r.t air is

Answer»

a/e
b/e
b/d
d/b

Answer :C
Discussion
45307.

An a.c. circuit has a chock coil L and resistance R. The potential difference across the chocke is v_(L) = 160 V and that across the resistance v_(R) = 120V. Find the virtual value of the applied voltage. If the virtual current in the circuit be 1.0 A, then calculate the total impedance of the circuit. If a direct current be passed in the circuit, then what will be the potential difference in the circuit ?

Answer»


Answer :`E = 200 V, Z = 200 OMEGA, V_(R) = 120 V`
Discussion
45308.

Electric field due to an infinite sheet of charge having surface charge density sigma is E. Electric field due to an infinite conducting sheet of same surface density of charge is

Answer»

E/2
E
2E
4E

Answer :C
Discussion
45309.

A radioactive element has half life period 800 years. After 6400 years what amount will remain ?

Answer»

`1/2`
`1/16`
`1/8`
`1/256`

ANSWER :D
Discussion
45310.

A wheel of mass 1000kg has M,I. of 160 kgm^2 about its own axis . the radius of gyration is

Answer»

0.24 m
0.34 m
0.4 m
0.45 m

Answer :A
Discussion
45311.

Unpolarised light is incident on a plane surface heaving refractive index sqrt3. The angle of incidence at which reflected and refracted rays would become perpendicular to each other is

Answer»

<P>`15^(@)`
`30^(@)`
`45^(@)`
`60^(@)`

SOLUTION :Hint : REFLECTED and refracted rays are mutually perpendicular when ANGLE of incident is the polarizing angle i.e., `i=i_(p)=tan^(-1)(n)=tan^(-1)(sqrt3)=60^(@).`
Discussion
45312.

Figure shows the variation of intensity of magnetisation vecM versus the applied magnetic field intensity vecH for two materials A and B: (a) Identify the materials A and B. (b) Why does the material B, have a larger susceptibility than A for a given field at constant temperature ?

Answer»

Solution :(a) Material A is DIAMAGNETIC because its magnetisation is negative
Material B is PARAMAGNETIC having positive magnetisation .
(b) Magnetic susceptibility ` x = M/H` and its VALUE is given by slope of M - H CURVE. As slope of curve for material B is greater, hence B has a large susceptibility than A for a given FIELD at constant temperature.
Discussion
45313.

The position of an object moving along x-axis is given by x=a+bt^(2) where a =8.5 m, b=2.5 ms^(-2) and t is measured in seconds.Then which of the following is true ?

Answer»

VELOCITY at t=2 SEC is zero
Average velocity between t=2,t=4 sec is 15 m/s
Velocity at t=4 sec is 10 m/s
All the above are true

Answer :B
Discussion
45314.

In the study of transistor as an amplifier alpha=I_C/I_E and beta=I_C/I_B where I_C,I_E and I_Bare the collector, emitter and base currents respectively. The correct relation between’ alpha and betais given by

Answer»

`BETA=(1-ALPHA)/alpha`
`beta=alpha/(1-alpha)`
`beta=(1+alpha)/alpha`
`beta=alpha/(1+alpha)`

ANSWER :D
Discussion
45315.

A car moving on a straight road accelerates from a speed of 4.1 m/s to a speed of 6.9 m/s in 5.0 s.What was its average acceleration?

Answer»

`0.56 m//s^(2)`
`1.56 m//s^(2)`
`5.6 m//s^(2)`
`1.2 m//s^(2)`

ANSWER :A
Discussion
45316.

Who are the pioneers in the field of electromagnetic waves ?

Answer»

SOLUTION :MAXWELL (1865),HERTZ (1887),MARCONI(1896,1899).
Discussion
45317.

The C.G.S, unit of universal gravitational constant is

Answer»

`6.67xx10^-11Nm^2//kg^2`
`66.73xx10^-11Nm^2//kg^2`
`6.67xx10^-8Nm^2//kg^2`
`6.673xx10^-13Nm^2//kg^2`

ANSWER :A
Discussion
45318.

Three is another useful system of units, besides the SI/mksA system, called the cgs (centimeter-gram -second) system, Coulumb's law is givenby F = (Qq)/(r^(2)) hat(r ) where the distance r is measured in cm (=10^(-2)m), F in dynes (=10^(-5) N) and the charges in electrostatic units (es units), where1 esunit of charge =(1)/([3]) xx 10^(-9) C The number [3] actually ariesfrom the speed of light in vacumm which is now taken to be exactly given by c = 2.99792458xx10^(8) m//s. An approximatevalue of c thenis c = [3] xx10^(8) m//s. (i) Show that the coulomb law in cgs units yields 1 esu of charge = 1 (dyn e)^(1//2)cm. Obtain the dimensious of units of charge in terms of mass M, length L and time T. Show that it is given in termsof fractional powers of M and L. (ii) Write 1 esu of charge = xC, wherex is a dimenionless number. Show that this gives (1)/(4pi in_(0)) = (10^(-9))/(x^(2)) (N.m^(2))/(C^(2)) Withx = (1)/([3]) xx10^(-9), we have (1)/(4pi in_(0)) = [3]^(2) xx10^(9) (Nm^(2))/(C^(2)) or (1)/(4pi in_(0)) = (2.99792458)^(2) xx 10^(9) (Nm^(2))/(C^(2)) (exactly).

Answer»

Solution :(i) From`F = (Qq)/(r^(2))`
`1 DYN e = ((1" esu of charge")^(2))/((1 CM)^(2))`
`:.` 1 esu of charge`= (1 dyn e)^(1//2) XX 1cm = F^(1//2). L = (MLT^(-2))^(1//2)` L or 1 esu of charg e ` = M^(1//2) L^(3//2) T^(-1)`.
Thus esu of charge is represented in terms of fractional powers`: (1)/(2) of M and (3)/(2) of L`
(ii) Let 1 esu fo charge = x C, where x is a dimenionless number
Coulomb forceon two charges, each of magnitude1 esu separatedby `1 cm is 1 dyne = 10^(-5) N`.
This situation is equivalent to two charges of magnitude x C separated by `10^(-2)m`.
`:. F = (1)/(4pi in_(0)) (x^(2))/((10^(-2))^(2)) = 1 dyne = 10^(-5) N :. (1)/(4pi in_(0)) = (10^(-9))/(x^(2)) (N m^(2))/(C^(2))`
Taking`x = (1)/(|3| xx10^(9))`, we get, `(1)/(4pi in_(0))= 10^(-9)xx |3| xx10^(18) (Nm^(2))/(C^(2)) = 9xx10^(9) (Nm^(2))/(C^(2))`
If `|3| rarr 2.99792458`, we get`(1)/(4pi in_(0)) = 8.98755xx10^(9) Nm^(2) C^(-2)`
Discussion
45319.

Two rods of lengths L_1 and L_2 are made of materials whose co-efficient of linear expansion arealpha _1 and alpha_2,If the difference between two lengths is independent of temperature , then

Answer»

a)`(L_1//L_2) = alpha_1/alpha_2`
B)`(L_1/L_2)= alpha_2/alpha_1`
C)`L_1^2alpha_1=L_2^2alpha_2`
d)`alpha_1^2L_1 =alpha_2^2L_2`

ANSWER :B
Discussion
45320.

A coil of N turns and area A is placed in a uniform transverse magnetic field B in such a way that vecA and vecB are parallel. If the plate in turned through 180^@ about its one of the diameter in 2 seconds then the (i) change of magnetic flux through the coil is ? (ii) rate of change of flux is the coil is ?

Answer»

SOLUTION :`Deltaphi=phi_2-phi_1`
`=NBA (COS theta_2-costhata_1)`
`= NBA(cos180^@-cos0)`
=NBA[-1-1]
=-2NBA
(ii)Rate of charge of flux is
`(Deltaphi)/(Deltat)=(-2NBA)/(2)`
=-NBA
Discussion
45321.

A cannon fires successively two shells with velocity v_(0) = 250 m//s, the first at the angle therefore= 60^(@) and the second at the angle q_(2) = 45^(@)to the horizontal, the azimuth being the same. Neglecting the air drag, find the time interval between firings leading to the collision of the shells.

Answer»

SOLUTION :Let the first shell travel for time `t_(1)` and second fortime `t_(2)` , before they collide .
Both the shells must travel equal horizontal and VERTICAL distances to collide.
For horizontal motion `v_(0) cos theta_(1) .t_(1) = v_(0) cos theta_(2) t_(2)`
`i.e., (t_(1))/(t_(2)) =(cos theta)/(cos theta_(2)) , (t_(1))/(t_(2)) = (cos 45^(@))/( cos 60^(@)) = (1//sqrt(2))/(1//2)t_(2)`
`i.e.,(t_(1))= sqrt(2) t_(2)`
For vertical motion ,
`v_(0) sin theta_(1). t_(1)- (1)/(2) "gt"_(1)^(2) = v_(0) sin theta_(2) . t_(2) = (1)/(2) "gt"_(2)^(2) (or) v_(0) sin 60^(@),t_(1) - (1)/(2)"gt"_(1)^(2) = v_(0) sin 45^(@) .t_(2) - (1)/(2) "gt"_(2)^(2)`
(or) `v_(0) ( sin 60^(@) t_(1) - sin 45^(@)t_(2)) = (g)/(2) (t_(1)^(2) -t_(2)^(2))`
Puttingvalues`250((sqrt(3))/(2)sqrt(2)t_(2)- (1)/(sqrt(2))t_(2)) = (9.8)/(2)(2t_(2)^(2) - t_(2)^(2))RARR 250((sqrt(6) - sqrt(2))/(2)) t_(2)= 4.9 t_(2)^(2)`
`t_(2) = (250(2.45-1.41))/(2 xx 4.9) (or) t_(2) = (250xx 1.04)/(9.8)= 26.7 s rArr t_(1) = sqrt(2) t_(2) = 1.414 xx 26.7= 37.8s`
Timeinterval `t_(1) - t_(2) = 37.8s - 26.7 s = 11.1 s`
Discussion
45322.

What amount of inpurity of atomic density in added toform N-type semiconductor in Ge semiconductor of conductivity sigma is 5Omega^(-1)cm^(-1) Mobility of electron in N-type semiconductoris 3900 cm^(2)V^(-1)s^(-1). Ignore conductivitydue to hole. (e=1.6xx10^(-19)C)

Answer»

`2.25xx10^(21)m^(-3)`
`4.007xx10^(21)m^(-3)`
`8013xx10^(21)m^(-3)`
`8.013xx10^(21)m^(-3)`

Solution :`8.013xx10^(21)m^(-3)`
`sigma=5Omega^(-1)cm^(-1)=500Omega^(-1)m^(-1)`
`mu_(e )=3900cm^(2)V^(-1)s^(-1)=0.39m^(2)V^(-1)s^(-1)`
Now `sigma=en_(e )mu_( e)`
`therefore n_(e )=(sigma)/(emu_(e ))`
`therefore n_(e )=(500)/(1.6xx10^(-19)xx0.39)`
`therefore n_(e )~~8.013xx10^(21)m^(-3)`
Discussion
45323.

All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly 0.6 But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) (hc=1250 eV-nm) What is the approximate temperature of the filament?

Answer»

500 k
350 k
2500 K
10000 K

Answer :C
Discussion
45324.

Name the pd between terminals of the cell when (i) key K is open(i) K is closed

Answer»

emf
lost voltage
terminal voltage
induced voltage

Answer :A
Discussion
45325.

The ground state energy of hydrogen atom is - 13.6 eV. If an electron makes a transition from an energy level - 0.85 eV to -3.4 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong?

Answer»

Solution :The groundstateenergy of hydrogen `E_(1)`= 13.6 eV .
`therefore ` Energy `E_(i) = -0.85e V` CORRESPONDS to a level `n_(i)`where ` - 0.85 = (-13.6)/(n_(i)^(2)) rArr n_(i) = 4`
Againenergy `E_(f) = - 3.4` eV correspondsto a level `n_(f)`suchthat ` -3.4 = - (13.6)/(n_(f)^(2))`, which leads us totheresult `n_(f) = 2`
As transition is takingplace from `n_(i) = 4`level to `n_(f) = 2` levelthewavelenghtbelongs to Balmer series of hydrogen SPECTRUM .
The wavelenghtof spectrall lineis given by therelation.
`hv = (HC)/(lambda) = E_(i) = E_(f) =- 0.85 eV - (-3.4 eV) = + 2.55 eV`.
`therefore "" lambda = (hc)/(2.55ev) = (6.63 xx 10^(-34) xx 3 xx 10^(8))/((2.55 xx 1.60 xx 10^(-19))J)= 4.875 xx 10^(-7) m = 487.5` nm
Discussion
45326.

All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly 0.6 But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) (hc=1250 eV-nm) Which of the following resistances would have maximum surface temperature. All of them have a surface area of10mm^(2)and same emissivity

Answer»

<P>`1 Omega`
`2 Omega`
`3 Omega`
`4 Omega`

Solution :`(dQ)/(dt)=eAsigma(T^(4)-T_(0)^(4))`
`T_(max)Rightarrow(dQ)/(dt) max`
`P_(4)=100^(2)/4 P_(1)=(100/2.2)^(2)xx1`
`P_(2)=(100/2.2xx3/5)^(2)xx2`
`P_(3)=(100/2.2xx2/5)^(2)xx3`
Discussion
45327.

All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly 0.6 But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) (hc=1250 eV-nm) If we want of increase the number of photons emitted by the bulb in the visible region without changing the wattage, which method would be most appropriate?

Answer»

INCREASING emissivity by a factor of 2
increasing the radius of the FILAMENT by a factor of 2 and the length by a factor of 4.
decreasing the radius of the filament by a factor of 2 and the length by a factor of 4
doubling the VOLTAGE and decreasing the length of the filament by a factor of 2.

Solution :`(dN)/(DT)uparrowifTuparrow`
`(DQ)/(dt)=eAsigmaT^(4) TuparrowRightarrowAdownarrow`
Discussion
45328.

The intrinsic semiconductor becomes an insulator at

Answer»

`0^(@)`C
`-100^(@)`C
300 K
0 K

Solution :At 0 K an INTRINSIC semiconductor behaves as an insulator.
Discussion
45329.

A 150 W lamp emits light of mean wavelength of 5500Å. If the efficiency is 12% , find out the number of photons emitted by the lamp in one second.

Answer»

SOLUTION :`{:("NUMBER of photons emitted per second n" = (P lambda)/(HC),,P = 150 W),(,,lambda 5500Å),("If the efficiency is 12%," eta = (12)/(100) = 0.12,,h = 6.6 XX 10^(-34)Js),(n = (P eta lambda)/(hc),,c = 3 xx 10^(8) ms^(-1)):}`
`= (150 xx 0.12 xx 5500 xx 10^(-10))/(6.6 xx 10^(34) xx 3 xx 10^(8)) = (99000 xx 10^(-10))/(19.8 xx 10^(-26)) = 5000 xx 10^(16)`
`n = 5 xx 10^(19)`
Discussion
45330.

The frail woman in Mukesh's house is his

Answer»

mother
elder BROTHER's wife
wife
niece

Answer :B
Discussion
45331.

Ionosphere can reflect which type of waves ?

Answer»

MICROWAVES
Radiowaves
X-rays
y-rays

Answer :B
Discussion
45332.

Which one of the following has the dimensions of[ML^(-1)T^(-2)]:

Answer»

torque
surface tension
viscosity
stress

Solution :stress `=("Force")/("area")=(MLT^(-2))/(L^(2))=[ML^(-1)T^(-2)]`
So CORRECT ANSWER is `(d)`
Discussion
45333.

A step down transformer has 50 turns on secondary and 1000 turns on primary winding. If a transformer is connected to 220 V 1 A A.C. source, what is output current of the transformer ?

Answer»

`1//20 A`
20 A
100 A
`2 A`

SOLUTION :`(N_(s))/(N_(p)) = (V_(s))/(V_(p))`
`(50)/(1000) = (V_(s))/(220)`
`V_(s) = 11 V`
`V_(s)I_(s) = V_(p)I_(p)`
`11 xx I_(s) = 220 xx 1`
`I_(s) = 20 A`
Discussion
45334.

A tall man of height 6 feet, want to see his full image. Then required minimum length of the mirror will be:

Answer»

12 FEET
3 feet
16 feet
Any length

ANSWER :B
Discussion
45335.

What is the magnetic field along the axis and equatorial line of a bar magnet ?

Answer»

Solution :Magnetic field at a point along the equatorial line due to a magnetic DIPOLE (bar magnet)
Consider a ber magnet. NS. Let N be the north pole and S be the south pole of the bar magnet, each with pole strength `q_(m)` and separated by a distance of 2l. The magnetic field at a point C (lies along the equatorial line ) at a distance r from the geometrical center O of the bar magnet can be computed by keeping unit north pole `(q_(m) C = 1 A m )` at C. The force e`xx`perienced by the unit north pole at C due to pole strength N-S can be computed using Coulomb.s law of magnetism as follows ,
the force of repulsion between North Pole of the bar magnet and unit north pole at point C (in free space ) is
`vec(F_(N)) = - F_(N) cos theta hat(i) + F_(N) sin theta hat(j) `
Where `F_(N) = (mu_(0))/(4pi ) (q_(m))/(r.^(2))` The force of attraction ( in free space ) between southpole of the bar magnet and unit north pole at point C is
`vec(F_(S)) = - F_(S) cos theta hat(i) - F_(S) sin theta hat(j)`
where , `vec(F_(S)) = (mu_(0))/(q_(m))(q_(m))/(r.^(2))`
From equation (1) and equation (2) , the net force at poin C is `vec(F) = vec(F_(N)) + F_(S)`. This net force is equal to the magnetic field at the point C .
`vec(B) - (F_(N) + F_(S)) cos theta hat(i)`
since, `F_(N) = F_(S)`
`vec(B) = - (2mu_(0))/(4pi) (q_(m))/(r.^(2)) cos theta hat(i) = (2 mu_(0))/(4pi ) ( q_(m))/((r^(2) + l^(2))) cos theta hati`
In a right angle TRIANGLE NOC as shown in the Figure l
cos `theta= ("adjacent")/("hypotenuse") = (l)/(r.) = (l)/((r^(2) + l^(2))^((1)/(2)))`
Substituting equation 4 in equation 3 we get
`vec(B) = - (mu_(0))/(4pi) (q_(m) xx (2l))/((r^(2) + l^(2))^((3)/(2)) )`
Since, magnitude of magnetic dipole moment is `|vec(P_(m))| = P_(m) = q_(m). 2l` and substituting in equation (5 ). The magnetic field at a point C is
`vec(B)_("equatorial") = - (mu_(0))/(4pi) (P_(m))/((r^(2) + l^(2))^((3)/(2)) )`
If the distance between two poles in a bar magnet are small (lools like short magnet ) when compared to the distance between geometrical center O of bar magnet and the location of point C i.e., r `gt gt ` l, then ,
`(r^(2) + l^(2))^((3)/(2)) approx r^(3)`
Therefore, using equation (7) in equation (6), we get
`vec(B)_("equatorial") = - (mu_(0))/(4 pi ) (P_(m))/(r^(3)) hat(i)`
Since, `P_(m) hat(i) = vec(P_(m)) . ` in general, the magnetic field at equatorial point is GIVEN by
`vec(B_("equatorial")) = - (mu_(0))/(4 pi ) (P_(m))/(r^(3))`
Note that magnitude of `vec(B_("axial")) `is twice that of magnitude of `B_("equatorial")` and the direction of `B_("axial ")and B_("equantorial") ` are opposite .
Discussion
45336.

A lamp is connected in series with a capacitor. Predict your observations for dc and ac connections. What happens in each case if the capacitance of the capacitor is reduced ?

Answer»

SOLUTION :When DC source is connected bulb will glow gradually more and more . When AC source is connected , bulb will glow with LESS brightness. When inductance is decreased, this brightness will INCREASE.
Discussion
45337.

Consider an equilateral triangle ABC of side 2a in the plane of the paper as shown. The centroid of the triangle is O. Equal charges (Q) are fixed at the vertices A, B and C In what follows consider all motion and situations to be confined the plane of the paper. (a) A test charge (q), of same sign as Q is placed on the median AD at a point at a distance delta below O. Obtain the force (vec(F)) felt by the test charge. (b) Assuming delta lt lt a discuss the motion of the test charge when it is released. (c) Obtain the force (vec(F)_(D)) on this test charge if it is placed at the point D as shown in the figure. (d) In the figure below mark the approximate locations of the equilibrium point (s) for this system. Justify your answer. (e) Is the equilibrium at O stable or unstable if we displace the test in the direction of OP ? The line PQ is parallel to the base BC. Justify your answer. (f) Consider a rectangle ABCD. Equal charges are fixed at the vertices A, B, C and D. O is the centroid. In the figure below mark the approximate locations of all the neutral points of the system for a test charge with same sign as the charges on the vertices. Dotted lines are drawn for the reference. (g) How many neutral points are possible for a system in which N charges are placed at the N vertices of a regular N sided polygon ?

Answer»

Solution :(a) `vec(F)=(2KQq(a/sqrt(3)-delta))/((a^(2)+(a/sqrt(3)-delta)^(2))^(3//2))-(KQq)/(((2a)/sqrt(3)+delta))` Here `K=1//4 pi epsi_(0)` and direction is upward (towards A)
(B) Using binomial approximation, `vec(F)=KQq (9 sqrt(3))/16 delta/a^(3)` (upward) which is linear in`delta`. Hence charge will oscillate simple harmonically about O when relaesed.
(c) `vec(F)_(D)=(KQq)/(3a^(2))` (downward)
(d) For small `delta` force on the test charge is upwards while for LARGE `delta` (eq. at D) force is downwards. So there is a neutral point between O and D. By symmetry there will be neutral points on other medians also. In figure x. Below all possible (4) neutral points are shown by.

(e) Let the distance along P be x and O to be at (0, 0). electric potential of a test charge along OP can be written as `V(x)=(Kq)/sqrt(x^(2)+(4//3))+(KQ)/sqrt((x+1)^(2)+(1//3))+(KQ)/sqrt((x-1)^(2)+(1//3))~~KQ sqrt(3/4) (3+9/16 x^(2))`
We can see that `V(x) prop x^(2)`, hence it is STABLE equilibrium.
(f) Equilibrium points are INDICATED by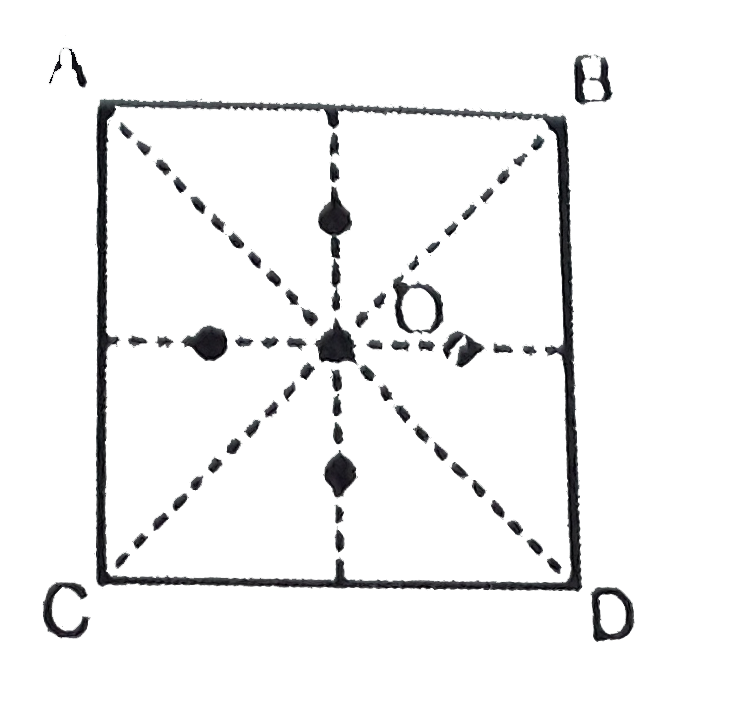

(g) `N+1`
Discussion
45338.

Both in interference and diffraction phenomena, alternate dark and bright fringes are obtained on screen I) generally fringe width is same in interference and not same in diffraction II) the central fringe in interference has maximum brightness and the intensity gradually decreases on either side III) in interference the intensity of all bright fringes is same IV) both the phenomena are produced from same coherent sources.

Answer»

I only
I and II
I, II and IV
I, III and IV

Answer :D
Discussion
45339.

Calculate the potential difference and the energy stored in the capacitor C_2 in the circuit shown in the Fig. Given potential at A is 90 V , C_1 = 20 mu F , C_2 = 30 mu Fand C_3 = 15 mu F

Answer»

Solution :Let as SHOWN in Fig `V_1 , V_2` and `V_3` be the respective potential differences across the capacitors `C_1 , C_2` and `C_3` respectively . In series combination same charge Q exists on each capacitor and `V_1 : V_2 : V_3 = (1)/(C_(1)) : (1)/(C_(2)) : (1)/(C_(3))`
`implies V_(1)= (C_(2))/(C_(1)) V_(2) = (30)/(20) V_(2)` and `V_(3) = (C_(2))/(C_(3)) V_(2) = (30)/(15) V_(2)`
But `V_(1) + V_(2) + V_(3) = 90 V` , hence we have
`(30)/(20) V_(2) + V_(2) + (30)/(15) V_(2) = 90 V implies 45 V_(2) = 90 V implies V_(2) = 20 V `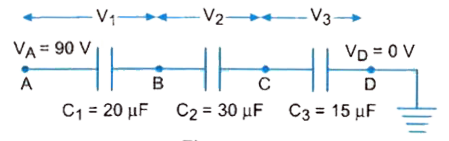

Moreover , energy stored in capacitor `C_2` is `V_2 = (1)/(2) C_(2) V_(2)^(2) = (1)/(2) xx (30 mu F) xx (20 V)^(2) = 6000 mu J = 6.0 mJ`
Discussion
45340.

A circuit shown in the figure has resistances 20 Omega and 30 Omega. At what value of resistance R_(x) will the thermal power generated in it be pracitcally independent of small variations of that resistance? The voltage between points A and B is supposed to be constant in this case.

Answer»

`3 OMEGA`
`7 Omega`
`12 Omega`
`20 Omega`

Answer :C
Discussion
45341.

Blood is flowing at a rate of 200 (cm)^3/sec in a capillary of cross sectional area 0.5 m^2. The velocity of flows in (in mm/sec)

Answer»

a)0.1
b)0.2
c)0.3
d)0.4

Answer :D
Discussion
45342.

Explain electric field and also electric field is point charge.

Answer»

Solution :Suppose, charge Q is placed at origin .O. in free SPACE. If another charge q is placed distance r at point P (OP =r), then Coulomb force acts on q.
`vecF = 1/(pi epsilon_(0)).(Qq)/r^(2)hatr`
If Q = 1C, then force acting on unit charge is called electric field E.
`therefore vecF/q = 1/(4PI epsilon_(0)).Q/r^(2) hatr`
`therefore vecE = 1/(4pi epsilon_(0)).Q/r^(2)hatr` or `E = (kQ)/r^(2)`
Definition of electric field : The region around the charge in which the effect of electric charge is PREVAILING is called the electric field of the charge.
Electric field `vecE` is also called electric fielt intensity. Force acting on charge q of position vector `vecr` is `vecF(vecr) =qvecE(vecr)`
Electric field `vecE` is also called electric field intensity.
Definition of Electric field : .The force acting on a unit positive charge at a given point in an electric field of a point charge of the system at charge is called the electric field or intensity of electric field `vecE`at that point.
SI unit of electric field intensity is `NC^(-1)` or `VM^(-1)`and DIMENSIONAL formula is `[M^(1)L^(1) T^(-3) A^(-1)]`
Discussion
45343.

Four equal point charges of 16 muCare kept at vertices of square of side 0.2 m. Find force acting at any one charge.

Answer»


ANSWER :`F = 110.3 N`
Discussion
45344.

In the Q. 122 what will be the velocity of the particle when it returns to the starting point?

Answer»

`vecr_(0)`
`-vecr_(0)`
`2vecr_(0)`
`-2vecr_(0)`

SOLUTION :`vecr=vecr_(0)t-vecr_(0)at^(2)`
`RARR VECV=(dvecr)/(dt)=vecr_(0)-vecr_(0)a2t`
Returning at `t=(1)/(a)`
`rArr vecv_(1//a)=vecr_(0)-2vecr_(0)axx(1)/(a)`
`rArr vecv=-vecr_(0)`
Discussion
45345.

In a common emitter amplifier , output resistance is 500Omega and input resistance is 2000 Omega . If peak value of signal voltage is 10 mV and beta =50 , then the peak value of output voltage is :

Answer»

`5 xx10^(-6)V`
`2.5 xx10^(-4)V`
1.25 V
125 V

Answer :C
Discussion
45346.

The current in resistance R_(3) in the given circuit is (2)/(x)A Find the value of x.

Answer»


ANSWER :3
Discussion
45347.

Magnetic flux passing through a coil varies with time as, phi=(2t^(2)-4) weber, Resistance of the coil is 10Omega.

Answer»

At time t=2s, induced CURRENT in the COIL is 0.8A
Induced current increases lineralu with time
From t=0 to t=2s,0.8C charge has flown in the coil
in the above time interval net flow of charge is zero

Answer :A::B::C
Discussion
45348.

Two polaroids are placed 90^(@) to each other and the transmitted intensity is zero. What happens when one more polaroid is placed between these two bisecting the angle between them?

Answer»


ANSWER :`1/4`
Discussion
45349.

Draw the voltage-current characteristic of a Zener diode.

Answer»

SOLUTION :
Discussion
45350.

A narrow slit illuminted by light of wavelength 0.64 mu is placed at a distance of 3 m from a straight edge. If the distance between the straight edge and the screen is 6 m calculate the ditance between the first and fourth dark bands.

Answer»

SOLUTION :`4.8xx10^(-3) m`
Discussion