Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 45201. |
Assertion:Naturally , thermonuclear fusion reaction is not possible on earth. Reason : For thermonuclear fusion to take place, extreme condition of temperatureand pressure are required . |
|
Answer» If both assertion and reason are TRUE and reason is the correct EXPLANATION of assertion . |
|
| 45202. |
What is the total change in energy when a positive charge is taken round a closed loop in an electrical network ? |
| Answer» Solution :ZERO. This is KIRCHHOFF's VOLTAGE law or LOOP law. | |
| 45203. |
For protecting a sensitive equipment from external magnetic field, it should be |
|
Answer» PLACED inside an ALUMINIUM can |
|
| 45204. |
(A): If a current flows through a wire of non uniform cross-section,potential difference per unit length of wire in direction of current is same at different points (R): ohms law V = iR is not valid for a wire of non-uniform cross-section |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the correct EXPLANATION of 'A' |
|
| 45205. |
Fig. Shows a concavo-convex lens. What is the condition on the refractive indices so that the lens is diverging ? |
|
Answer» `2mu_3 LT mu_1+ mu_2` |
|
| 45206. |
In a large building, there are 15 bulbs of 40W, 5 bulbs of 100 W, 5 fans of 80 W and 1 heater of 1 kW. The voltage of the electric mains is 220 V. The minimum capacity of the main fuse of the building will be |
| Answer» Answer :B | |
| 45207. |
Infrared radiations are detected by: |
|
Answer» Spectrometer |
|
| 45208. |
Two particles of masses m and 2m are placed on a smooth horizonttal table. A string, which joins these two masses, hangs over the edge supporting a pulley, which suspends a particle of mass 3m, as shown in Fig. 5-40. The pulley has negligible mass. The two parts of the string on the table are parallel and perpendicular to the edge of the table. The hanging parts of the string are vertical. Find the acceleration of the particle of mass 3m. |
| Answer» SOLUTION :`5.2" m"//"s"^(2)` | |
| 45209. |
A triangular wedge of mass M is moving with uniform velocity v_(0) along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m. |
|
Answer» Solution :LINE of impact is a STRAIGHT line perpendicular to the incline. Normal reaction force between the body and the wedge acts along the impact line. This normal force becomes internal force when we consider (wedge + body) as a total system. But normal reaction is considerable in MAGNITUDE because the impact force during collision has contribution towards making of the normal force. Momentum of the system is conserved along the line perpendicular to this normal force.....(i) Momentum of the system is conserved along horizontal.....(ii) Momentum of the particle is conserved along the common tangent at the point of impact......(iii) As this is an elastic collision, relative velocity of separation along the impact line = Relative velocity of approach......(IV) If the wedge were at rest then the particle would deflect along the horizontal after collision because it is an elastic collision.....(v) As, in this case, wedge is moving, the OBJECT would not be deflected horizontal, but at an angle `.alpha.` to the line of impact....(vi) Velocity of particle before impact `u=sqrt(2gh)` along `vec(PO)` Velocity of particle after collision `= v_(1)` along `vec(OQ)` Velocity of wedge before collision `= v_(0)` along `vec(RO)` Velocity of wedge after collision `= v_(2)` along `vec(RO)` Velocity of approach = velocity of separation `v_(0)cos 45^(@)-ucos 45^(@)=-v_(1)cos alpha - v_(2)cos 45^(@)` `rArr v_(1)cos alpha + (v_(2))/(sqrt(2))=(u)/(sqrt(2))-(v_(0))/(sqrt(2))` `sqrt(2)v_(1)cos alpha + v_(2)=u-v_(0) "" ....(A)` Conserving momentum along the horizontal `Mv_(0)=Mv_(2)-mv_(1)cos (45^(@)-alpha)` `rArr 2v_(0)=2v_(2)-v_(1)cos (45^(@)-alpha)` `rArr 2v_(2)-v_(1)cos(45^(@)-alpha)=2v_(0) ""`....(B) Conserving momentum along the common tangent `mu sin 45^(@)=mv_(1)sin alpha` `rArr v_(1)sin alpha = u ""`....(C ) On solving (A), (B) and (C ) `v_(1)=sqrt(u^(2)[(u(4-sqrt(2))-6v_(0))/(20)]^(2))` and `v_(2)=(v_(0)+(sqrt(2)+1)u)/(5)` 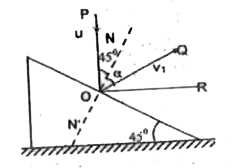
|
|
| 45210. |
A galvanometer having a coil of resistance 12 Ωgives full scale deflection for a current of 4 mA. How can it be converted into a voltmeter of range 0 to 24V. |
|
Answer» Solution :`G= 12 OMEGA I_(g) =4A ,V =24 V` `R=(I)/(I_(g))-G` =6000-12 =5988 R=5988 `omega`By CONNECTING this high resistance in SERIES with the GALVANOMETER we can convert galvanometer into a voltmeter. |
|
| 45211. |
A stretched string has a mass per unit length of 5.00 g/cm and a tension of 10.0 N A sinusoidal wave on this string has an amplitude of 0.16 mm and a frequency of 100 Hz and is traveling in the negative direction of an x axis. If the wave equation is of the form y(x,t)= y_m sin(kx pm omegat), what are (a) y_m (b) k. (c) omega, and (d) the correct choice of sign in front of omega? |
|
Answer» |
|
| 45212. |
Which of the following is regarding mutual inductance? |
|
Answer» UNIT of M is henry |
|
| 45213. |
A heat conducting piston can move freely inside a closed, thermally insulated cylinder with an ideal gas (gamma= 5/3). At equilibrium, the piston divides the cylinder into two equal parts, the gas temperature being equal to 300 K. The piston is slowly displaced by an external agent. Find the gas temperature when the volume of the greater section is seven times the volume of the smaller section. |
|
Answer» |
|
| 45214. |
Two gases O_2 and H_2 are at the same temperature . If E_o is the average kinetic energy of a molecule of oxygen sample , and E_H is the average kinetic energy of a molecule of hydrogen sample , then |
|
Answer» `E_o=1/16E_H` |
|
| 45215. |
An electron and a photon each have a wavelength of 1.00 nm. Find (a) their momenta, (b) the energy of the photon, and (c) the kinetic energy of electron. |
|
Answer» Solution :Here `lamda=1.00nm=1.00xx10^(-9)m` (a) Momentum of electron momentum of photon `p=(h)/(lamda)=(6.63xx10^(-34))/(1.00xx10^(-9))=6.63xx10^(-25)KG" "MS^(-1)`. (B) Energy of photon `E=(HC)/(lamda)p*c=6.63xx10^(-25)xx3xx10^(8)=1.989xx10^(-16)J` `=(1.989xx10^(-16))/(1.6xx10^(-19))eV=1.24xx10^(3)eV or 1.24keV`. (c) Kinetic energy of electron `K=(p^(2))/(2m)=((6.63xx10^(-25))^(2))/(2xx9.11xx10^(-31))=2.413xx10^(-19)J` `=(2.413xx10^(-19))/(1.6xx10^(-19))eV=1.51eV`. |
|
| 45216. |
The penetrating powers of alpha and betaand radiations, in decreasing order, are |
|
Answer» `GAMMA, ALPHA , BETA` |
|
| 45217. |
In a two dimensional x – y plane, the magnetic field lines are circular, centred at the origin. The magnitude of the field is inversely proportional to distance from the origin and field at any point P has magnitude given by B = k /r, where k is a positive constant. A wire carrying current I is laid in xy plane with its ends at point A (x_(1), y_(1) and point B (x_(2)), y_(2)). Find force on the wire. |
|
Answer» |
|
| 45218. |
Resistivity of material does not depend on ...... of conductor |
|
Answer» TEMPERATURE |
|
| 45219. |
Two bulbs are rated (P_1, V)"and"(P_2, V) . If they are connected (i) in series and (ii) in parallel across a supply V, find the power dissipated in the two combinations in terms of P_1 and P_2. |
|
Answer» Solution :Resistance of given bulbs are `R_1 = (V^2)/(P_1) " and " R_2 = (V^2)/(P_2)` (i) In series grouping net resistance `R_s = R_1 + R_2`. If `P_s` be the power dissipated in series arrangement then `R_s = (V^2)/(P_s)` `rArr (V^2)/(P_s) = (V^2)/(P_1) + (V^2)/(P_2) rArr (1)/(P_s) = (1)/(P_1) + (1)/(P_2) rArr P_s = (P_1 P_2)/(P_1 + P_2)` (II) In PARALLEL grouping EQUIVALENT resistance `R_P = (V^2)/(P_P)` is given as PER relation : `(1)/(R_P) = (1)/(R_1) + (1)/(R_2) rArr (P_P)/(V^2) = (P_1)/(V^2) + (P_2)/(V^2) rArr P_P = P_1 + P_2` |
|
| 45220. |
Complete the following statement about photo electric effect. The radiations having minimum frequency called............... falls on a metallic surcace, electrons are emitted from it. The metal which emits photoelec trons are called........... The kinetic energy of pho toelectrons emitted by a metal depends on of.......... the radiations. |
| Answer» Solution :THRESHOLD FREQUENCY, PHOTOSENSITIVE frequency NUMBER of photons | |
| 45221. |
Moving particles of matter should display wavelike properties under suitable conditions. A photon and electron have got the same wavelength. Explain which has got greater energy? |
| Answer» SOLUTION :Energy of PHOTON `E_1=HV=(hv)/lambda` Energy of electron `E_2=mc^2=(hc^2)/(lambdav^2 ` i.e`E_2>E_1` or electron has greater energy | |
| 45222. |
The length of the antenna (a) limits the frequency of EM waves to be radiated (b) makes the users to opt for Higher frequency transmission © is insignificant during transmission. |
|
Answer» a & b are true |
|
| 45223. |
How can you detect a polarized light? |
Answer» Solution :Take two tourmaline CRYSTALS `T_(1)` and `T_(2)` cut with their FACES PARALLEL to the axis of the crystal. A FINE beam of light from the source S is passed through `T_(1)` and light is observed by placing eye behind `T_(2)`. 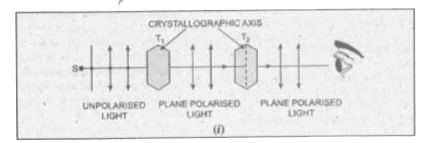 When the axis of `T_(1)` and `T_(2)` are parallel, maximum light is observed [Fig. (i)] but when the axis of `T_(1)` and `T_(2)` are crossed (PERPENDICULAR), then practically no light is observed. This phenomenon can only be explained if light waves are transverse. Light falling on `T_(1)` has transverse vibrations lying in all possible directions. `T_(1)` allows only vibrations which are parallel to the axis of `T_(1)` . If second crystal `T_(2)` is placed parallel to `T_(1)` as in first figure, then vibrations transmitted by `T_(1)` are also transmitted by `T_(2)`. If `T_(2)` is perpendicular to `T_(1)`, the vibrations from `T_(1)` are perpendicular to the axis of `T_(2)`. Hence `T_(2)` will not allow these vibrations to pass [Fig. (ii)]. Longitudinal vibrations can however pass through slits irrespective of their orientations. This is the reason as to why the sound waves cannot be polarised. Due to the change of the intensity of polarised light as a result of relative orientation of their crystallographic axis, it is concluded that the light waves must be transverse in nature. |
|
| 45224. |
Luminous intensites of two sources of light are compared using a |
|
Answer» POLARIMETER |
|
| 45225. |
Derivesigma=("ne"^2 tau)/m, where the symbols have their usual meaning. |
|
Answer» Solution :Let .n. be the numberdensityof electrons , .L. be the lengthof the CONDUCTORA and .A.be the areaof cross -sectionof the conductor . Let `v_d` be the drift VELOCITYOF the electrons and Dx be a small length . Electrons drift in a directionoppositeto the electric field. Number ofelectronsin .Dx.and area of cross -section .A.is equal to (ADx) n. Charge on the theseelectrons =(nADx)e. If Dt is the time taken for effectivedisplacementof electronsthen rate of flow charge = `nAe ((Deltax)/(Deltat))` . By DEFINITION,electric current I=rate of flowof charge i.e.,`I=nAev_d`...(1) where , average velocityof electrons with whichit drifts againstthe directionof electric field is known as drift velocity`(v_d)`. Let .a. be the accelerationof electrons. Let .E.be the electricfieldintensity . Force on electrons, F=ma i.e., eE=ma But = `a=v_dt` where .t.is the relaxationtime . Relaxationtime representsthe average timetaken for two successivecollisionsof electronsand ionsin the lattice. 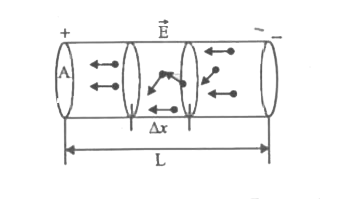 Hence ,`eE=mv_dt` or `v_d=(eE)/(mtau)` ...(2) We alsoknow that electricpotentialdifferencebetween the ends of the conductorV=EL `v_d =(eV)/(mtauL)` substitutingthis is the expression (1) We write, `I=nAe ((eV)/(mtauL))` i.e., `I=((nAe^2)/(mtauL))V` `R=(mtau L)/(nAe^2)`is called the electricalresistanceof a conductor . and `K=((nAe^2)/(mtauL))` is called the electric conductance of a conductor . the expression `sigma =("NE"^2)/(mtau)` is called the electricalconductivityand `1/sigma=(mtau)/("ne"^2)` is called electricalresistivity . |
|
| 45226. |
In a head-on collision between an alpha-particle and a gold nucleus, the distance of closest approach is 39.5 fermi. Calculate the energy of alpha-particle. For gold Z=79. |
|
Answer» As `E=(Ze(2e))/(4 pi epsilon_(0)R)=(2 Ze^(2))/(4 pi epsilon_(0)r)` `=(9xx10^(9)xx79xx2xx(1.6xx10^(-19))^(2))/(39.5xx10^(-15))` `=(9xx79xx2xx1.6xx1.6xx10^(-14))/(39.5)J` or `E=(18xx79xx1.6xx1.6xx10^(-14))/(39.5xx1.6xx10^(-13))` `=5.76` M eV. |
|
| 45227. |
If an earth satellite is put in orbit at a height where resistance due to the atomosphere cannot be neglected, how will the motion of a satellite be affected ? |
| Answer» Solution :For a satellite, moving in a circular ORBIT of RADIUS r orbital velocity `V_0=sqrt((GM)/r)THEREFORE Its K.E.=1/2mV_0^2=^1//_2m(GM)/r=^1//_2(GMM)/(2.r)and it's ` PE(GMm)/rxxr/(GMm)=^1//_2` | |
| 45228. |
There is no charge on 3F capacitor when .S. is open. Much heat (in Joule) is developed in circuit after .S. is closed ? |
|
Answer» |
|
| 45229. |
In the circuit shown in the figure, if both the bulbs B_(1) and B_(2) are identical |
|
Answer» their brightness will be the same |
|
| 45230. |
A rectangular coil of 20 turns and area of cross-section 25 square cm has a resistance of 100 ohm. If a magnetic field which is perpendicular to the coil change at a rate of 100 tesla per sec,the current in the coil is : |
|
Answer» 1.0 AMPERE |
|
| 45231. |
Watt is the unit of |
|
Answer» force |
|
| 45232. |
What is the shape of the wavefront in each of the following cases: (a) Light diverging from a point source. (b) Light emerging out of a convex lens when a point source is placed at its focus. (c) The portion of the wavefront of light from a distant star intercepted by the Earth. |
| Answer» Solution :Wavefronts emitted from distant star and then PROPAGATING in three dimensional HOMOGENEOUS and isotropic medium are found to be plane locally at very large distance from that star (i.e, on the EARTH). HENCE small portion of such wavefronts OBSERVED from Earth will be "Plane Wavefronts". | |
| 45233. |
Wavelength of radiations emitted, when an electron jumps from a state A to C is 2000 Å and it is 6000 Å, when the clectron jumps from state B to state C. Wavelength of the radiations emitted, when an electron jumps from state A to B will be: |
|
Answer» 2000 Å Here `lambda_(3)=2000Å, lambda_(1)=6000Å," then "lambda_(2)=3000Å` |
|
| 45234. |
Large band width for higher data is achieved by using |
|
Answer» high FREQUENCY carrier WAVE |
|
| 45235. |
A uniform rectangular block has length twice as large as the breath. It is lying on the horizontal plane, which is gradually being raised so as to be inclined to the horizontal at an angle theta. For what value theta, the block be at the point of toppling? |
|
Answer» `70.6^(@)`  `therefore TANTHETA=((a)/(2))/(a)=0.5impliestheta=26.6^(@)` |
|
| 45236. |
For series combination total resistance R will be: |
|
Answer» `(1)/(R)=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))+ . . .. ` |
|
| 45237. |
A 10 kg box is placed on a surface. Coefficient of friction between surface and box is u = 0.5. Horizontal force of 100N is applied. Acceleration of block will be : |
|
Answer» `2.5 m//s^(2)` |
|
| 45238. |
A block A of mass 6kg is applied on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 4kg at the other end. Find the acceleration of the system and tension in the thread (given g=10ms^(-2)) |
|
Answer» |
|
| 45239. |
Change in temperature |
|
Answer» increases FORWARD resistance |
|
| 45240. |
An isolated nucleus which was initially at rest, disintegrates into two nuclei due to internal nuclear forces and nogamma rays are produced. If the ratio of their kinetic energy is found to be |
|
Answer» <P>RATIO of their de-broglie wavelength is `(sqrt(64))/(sqrt(27))` respectively `m_(1)v_(1)=m_(2)v_(2)` `((P^(2))/(2m_(1)))//((P^(2))/(2m_(2)))=64/27` `(m_(2))/(m_(1))-64/27 =(v_(1))/(v_(2))` `(lambda_(1))/(lambda_(2))=(h//P_(1))/(h//P_(2))=1:1` `(R_(1))/(R_(2))=((A_(1))/(A_(2)))^(1//3)=3/4` |
|
| 45241. |
A shell, which is initially located at a distance of 40.4 m above a horizontal plane, is fired horizontally with a muzzle velocity of 285 m/s to strike a target on the horizontal plane. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does the shell strike the plane? What are the magnitudes of the (c ) horizontal and (d) vertical components of its velocity as it strikes the ground? |
| Answer» SOLUTION :(a) `~~2.87s`, (B) 818 m, ( C) 285 m/s, (d) 28.1 m/s | |
| 45242. |
Is the dispersive power independent on the angle of the prism? Give reason. |
| Answer» Solution :Yes, it is. The DISPERSIVE POWER of the material of a PRISM DEPENDS only on the NATURE of the material. | |
| 45243. |
Three point charge have been placed along the x axis at points A, B and C. Distance AB = BC. The field lines generated by the system is shown in figure. (a) Plot the variation of electric potential along x axis. Show potential on y axis of your graph. (b) Plot the variation of electric potential along y axis with B as origin. Shows potential on x axis in your graph. |
|
Answer» (b). `(d)/(sqrt(3)-1)` (C). `(2KQ)/(d)(2-sqrt(3))` (d) `(-Q)/(in_(0))` |
|
| 45244. |
The work function of a metal is 3.0 V. It is illuminated by a light of wave length 3xx10^(-7)m.Calculate i) threshold frequency, ii) the maximum energy of photoelectrons, iii) the stopping potential. (h=6.63xx10^(-34)Js and c=3xx10^(8)ms^(-)). |
|
Answer» Solution :`W=hv_(0)=3.0eV=3xx1.6xx10^(-19)J` THRESHOLD frequency `v_(0)=(W)/(H)=(3xx1.6xx10^(-19))/(6.63xx10^(-34))=0.72xx10^(15)Hz` (ii) Maximum kinetic energy `(E_(max))=h(v-v_(0))` `lamda-3XX10^(-7)m,v=(c)/(lamda)=(3xx10^(8))/(3xx10^(-7))=1xx10^(15)Hz` `K_(max)=h(v-v_(0))` `=6.63xx10^(-34)(1-0.72)xx10^(15)J=1.86xx10^(-19)J`. (III) `K_(max)=eV_(0)` where `V_(0)` is stopping potential in volt and e is the charge of electron `V_(0)=(K_(max))/(e)`. Here `K_(max)=1.86xx10^(-19)J` and `e=1.6xx10^(-19)C" "V_(0)=(1.86xx10^(-19)J)/(1.6xx10^(-19)C)=1.16V` |
|
| 45245. |
A: Diamond glitters.R: Diamond doesn.t absorb sun light. |
|
Answer» Both ASSERTION and REASON are TRUE and the reason is CORRECT EXPLANATION of the assertion. |
|
| 45246. |
A plane progressive wave of frequency 25Hz amplitude 2.5 xx 10^(-5) m and initial phase zero propagates along negative x-direction with a Velocity of 300 m/s. At any instant, the phase difference between the oscillations at two points 6m apart along the line is phi and the corresponding amplitude difference is A. |
|
Answer» A=0 |
|
| 45247. |
Find the value of magnetic dipole moment (in Am^(2)) of the following circuit the current distribution is shown in the diagram. |
Answer» SOLUTION :`vecM_(1)+vecM_(2)=M=4r^(2)HATI` 
|
|
| 45248. |
In Figure, two isotropic point sources S_(1) and S_(2) emit light in phase at wavelength lambda and at the same amplitude. The sources are separated by distance 2d = 6.00 lambda. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance D = 20.0 lambda. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position x_(P). (a) At what value of x_(P) do the rays have the minimum possible phase difference? (b) What multiple of lambda gives that minimum phase difference? (c) At what value of x_(P) do the rays have the maximum possible phase difference? What multiple of lambda gives (d) that maximum phase difference and (c) the phase difference when x_(P)=6.00 lambda? (f) When x_(P)=6.00 lambda, is the resulting intensity at point P maximum, minimum, intermediate but closer to maximum, or intermediate but closer to minimum? |
| Answer» SOLUTION :(a) 0, (B) 0, (C) `infty`, (d) 12p, (e) 3.6p, (F) “intermediate” but CLOSER to a MINIMUM than to a maximum | |
| 45249. |
If sound waves of frequency 20 KHz are to transmitted directly, then the length of the anternna required is : |
|
Answer» 3.75 km |
|
| 45250. |
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire? |
| Answer» SOLUTION :`3.5 XX 10^(-5) T` | |