Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 45101. |
The earth magnetic field at the equator is approximately 04.G. Estimate the earth's dipole moment. |
|
Answer» Solution :From Eq (5.7), the equatorial magnetic field is `B_(E)=(mu_(0)m)/(4pi R^(3))` We are given that `B_(E)-0.4G=4 xx 106(-5)T.` For r we take the radius of the earth `6.4 xx 10^(6) m`. Hence `m=(4 xx 10^(-5) xx (6.4 xx 10^(6))^(3))/(mu_(0)//4pi)=4 xx 10^(2) xx (6.4 xx 10^(6))^(3) (mu_(0)//4pi=10^(-7))` `=1.05 xx 10^(23) Am^(2)` This is close to the VALUE of `8 xx 10^(22) A m^(2)` quoted in geomegnetic TEXTS. |
|
| 45102. |
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 "cm s"^(-1)in a direction normal to the (a) longer side, (b) shorter side of the loop ? For how long does the induced voltage last in each case ? |
|
Answer» SOLUTION :`(1) 2.4xx10^(-4) V , ` lasting 2S (2) `0.6xx10^(-4) V, ` lasting 8s |
|
| 45103. |
The resistivity of indium arsenide is 2.5xx10^(-3) ohm m, its Hall constant is 10^(-2)m^(3)//C. Assuming the conductivity to be due to carriers of one sign only, find the concentration and the mobility of the charge carriers. . |
|
Answer» |
|
| 45104. |
Show graphically, the variation of the de-Broglie wavelength (lambda) with the potential (V) through which an electron is accelerated from rest. |
Answer» SOLUTION :
|
|
| 45105. |
A projectile of mass m is thrown with a velocity v making an angle 60° with the horizontal. Neglecting air resistance, the change in momentum from the departure A to its arrival at B, along the vertical directions : |
|
Answer» 2mv HENCE `Deltap = mv sin 60° - (- mv sin 60°)` `2mv=sqrt(3)/2=sqrt(3)mv` |
|
| 45106. |
If the number of turns of a solenoid is doubled, keeping the other factors constant, how does the self-inductance of the solenoid change? |
|
Answer» |
|
| 45107. |
Ratio of number density of holes is (7)/(5) and ratio of their current is (7)/(4) in a semiconductor. The ratio of their drift velocity is ……. |
|
Answer» `(4)/(7)` CURRENT in semiconductor `I=nAv_(d)e` `THEREFORE v_(d)=(I)/(nAe)` `therefore v_(d ) prop (I)/(n) [because "A, e constant"]` `therefore ((v_(d))_(e))/((v_(d))_(h))=(I_(e ))/(I_(h))xx(n_(h))/(n_(e ))` `=(7)/(4) xx (5)/(7)=(5)/(4)` |
|
| 45108. |
Deuteron and a-particle are put 1A apart in air. Magnitude of intensity of electric field due to deuteron at a particle is : |
|
Answer» ZERO |
|
| 45109. |
An inductor of 5H inductance carries a steady current of 2A. How can a 50V self-induced emf to made to appear in the inductor? |
|
Answer» SOLUTION :L= 5H, |e| = 50V Let US produce the required emf by reducing current to zero. Now `|e|= L (dI)/(dt) or dt= (LdI)/(|e|)= (5 xx 2)/(50)s` `=(10)/(50)s= (1)/(5)s= 0.2s` So, the desired emf can be produced by reducing the given current to zero in 0.2 second. |
|
| 45110. |
The S.I. unit of inductive reactance is |
|
Answer» Henry |
|
| 45111. |
The strong neutron excess (defined as N - Z) of high- mass nuclei is illustrated by noting that most high-mass nuclides could never fission into two stable nuclei without neutrons being left over. For example, consider the spontaneous fission of a ""^(235)U nucleus into two stable daughter nuclei with atomic numbers 39 and 53. From Appendix F, determine the name of the (a) first and (b) second daughter nucleus. From Fig. 40-6, approximately how many neutrons are in the (c) first and (d) second? (e) Approximately how many neutrons are left over? |
|
Answer» |
|
| 45112. |
Select the correct answer out of the options given against each question and write in the box provided on rigth hand side bottom: The process in which the amplitude of the carrier wave is made proportional to the instantnaeous amplitude of the signal wave is called |
|
Answer» AMPLITUDE modulation |
|
| 45113. |
In a noiseless transformer, an alternating current of 2A is flowing in primary coil. The number of turns in primary and secondary coil are 100 and 20 respectively the secondary current is ......... |
|
Answer» Solution :`I_1`=2A , `N_1` = 100, `N_2`= 20 , `I_2`= ? `I_2/I_1=N_1/N_2` `therefore I_2=I_1 N_1/N_2 = (2xx100)/20`= 10 A |
|
| 45115. |
L is a long conducting thread and there is a small plate p which is earthed through C. Some amount of electricity will flow through C |
|
Answer» if a CURRENT fluctuates in the L |
|
| 45116. |
The dimensional formula of pressure is (1990) |
|
Answer» `[MLT^(-2) ]` |
|
| 45118. |
A beam of monochromatic light entering a glass window pane from the air will experience a change in |
|
Answer» FREQUENCY nad wavelength |
|
| 45119. |
In a plane electromagnetic ware the electric field oscillates sinusoidally at frequency of 2.0xx10^10 Hz and amplitude 48Vm^(-1).What is the amplitude of the oscillating magnetic field? |
| Answer» Solution :Amplitude of MAGNETIC FIELD `B_0=(E_0)/C=(48)/(3xx10^8)=1.6xx10^(-7).` | |
| 45120. |
In a plane electromagnetic ware the electric field oscillates sinusoidally at frequency of 2.0xx10^10 Hz and amplitude 48Vm^(-1).What is wagelength of the wave ? |
| Answer» Solution :Here `epsilon=48 Vm^(-1), f=2.0xx10^10 Hz C=3xx10^8 MS^(-1)` (i) Wavelength of the WAVE `lambda=C/f=(3xx10^8)/(2.0xx10^10) = 1.5xx10^(-2) m.` | |
| 45121. |
A particle executes S.H.M. with an amplitude of 2 cm. When the particle is at 1 cm from the mean position the magnitude of tis velocity is equalto that of its acceleration. Then its time periodin second is : |
|
Answer» `(1)/(2pi sqrt(3))` `sqrt(r^(2)-y^(2))=omega y=(2pi)/(T)y` `T=(2pi y)/(sqrt(r^(2)-y^(2)))=(2pi XX1)/(sqrt(2^(2)-1^(2)))=(2pi)/(sqrt(3))`second. Correct choice is ( c ). |
|
| 45122. |
Match the following |
|
Answer» Solution :a. is directlyproportional to CURRENT B. no battery is required C. shorter the de-Broglie WAVELENGTH d. electron volt |
|
| 45123. |
A telescope is an optical instrument used to increase the visual angle of distant objects such as stars, planets etc. An astronomical telescope consists of two converging lenses. The one facing the object is called objective and the lens close to the eye is called an eyepiece. It can be adjusted by displacing relative to the objective. The angular magnification is defined as the ratio of focal length of objective and eyepiece. One can see the image with unstrained eye if it forms at infinity. An astronomical telescope has an objective of focal length 50 cm and a magnification of 20. Q Focal length, of the eyepiece is |
|
Answer» 2.5 cm |
|
| 45124. |
Power factor in an L-C-R circuit is …….. |
|
Answer» 0 `COS delta=R/sqrt(R^2+(omegaL-1/(omegaC)^2)` but when RESONANCE occurs `omegaL=1/(omegaC.)` `therefore cos delta =R/R=1` |
|
| 45125. |
Two insulating plates are both uniformly charged in such a way that the potential difference between them is V_(2)-V_(1)=20V. (i.e., plate 2 is at a higher potential). The plates are separated by d = 0.1 m and can be treated infinitely large. An electron is released from rest on the inner surface of plate 1. What is its speed when it hits plate 2? |
|
Answer» |
|
| 45126. |
Figure shows a soap film formed between two square figures made of a uniform wire. The bigger square is held while keeping it in a horizontal plane and the smaller square is slowly allowed to droip vertically. It reaches an equilibrium state after dropping a height h. Let surface tension of soap =T. Mass per unit length of wire =lamda. Acceleration due to gravity =g Given that h=(nlamdaga)/(2sqrt(4T^(2)-lamda^(2)g^(2))), find the integer value n. |
|
Answer» `2xx4aTxxcostheta=4alamdag` `costheta=(lamdag)/(2T)` `impliesh=(3lamda GA)/(2sqrt(4T^(2)-LAMDA^(2)g^(2)))` 
|
|
| 45128. |
Find the ratio of magnetic moment of an electron to its angular momentum is an atomic orbit. |
|
Answer» SOLUTION :`(M)/(L)=(EVR)/(2xx m V r)` `(M)/(L)=( e )/(2m)`. |
|
| 45129. |
An air bubble of volume 15 cm is at the bottom of a lake 40 m deep, where the temperature is 4.0^@ C. The bubble rises to the surface, which is at a temperature of 20^@ C Take the temperature of the bubble's air to be the same as that of the surrounding water. Just as the bubble reaches the surface, what is its volume? |
| Answer» SOLUTION :`77 cm^3` | |
| 45130. |
In the pervious question ,what is the average velocity of the particle? |
|
Answer» ` 1 MS ^(-1)` Average velocity `=("TOTAL displacement ")/("Totaltime")=(2)/(4) =0.5 ms^(-1) ` |
|
| 45131. |
A telescope is an optical instrument used to increase the visual angle of distant objects such as stars, planets etc. An astronomical telescope consists of two converging lenses. The one facing the object is called objective and the lens close to the eye is called an eyepiece. It can be adjusted by displacing relative to the objective. The angular magnification is defined as the ratio of focal length of objective and eyepiece. One can see the image with unstrained eye if it forms at infinity. An astronomical telescope has an objective of focal length 50 cm and a magnification of 20. If object is at a distance 600m from the telescope to see the image with unstrained eye separation between two lenses should be ( in cm ) |
|
Answer» 46.65 |
|
| 45132. |
A telescope is an optical instrument used to increase the visual angle of distant objects such as stars, planets etc. An astronomical telescope consists of two converging lenses. The one facing the object is called objective and the lens close to the eye is called an eyepiece. It can be adjusted by displacing relative to the objective. The angular magnification is defined as the ratio of focal length of objective and eyepiece. One can see the image with unstrained eye if it forms at infinity. An astronomical telescope has an objective of focal length 50 cm and a magnification of 20. To view remote object by an unstrainednormal eye separation between two lenses will be |
|
Answer» 55 cm |
|
| 45133. |
A block of mass 10 kg is moving horizontally with aspeed of 1.5 m s^(-1)on a smooth plane. If a constant vertical force 10 N acts on it, the displacement of the block from the point of application of the force at the end of 4 second is |
|
Answer» 5 m The situation is as shown in the figure . Acceleration along VERTICAL DIRECTION `a_y=F/m ="10 N"/"10 kg" = 1 m s^(-2)` Distance travelled by the block in 4 s in vertical direction is `s_y=1/2a_yt^2=1/2xx(1 m s^(-2) )(4 s)^2`= 8 m Distance travelled by the block in 4 s in horizontal direction is `s_x=(1.5 m s^(-1))(4 s)`=6 m The displacement of the block at the end of 4 s is `=sqrt(s_x^2+s_y^2)=sqrt((8 m)^2 + (6 m)^2)`= 10 m 
|
|
| 45134. |
किसी बिंदु-वस्तु (point object) से निकलकर किरणें किसी लेंस से अपवर्तित होकर जिस बिंदु पर मिलती है, उसे कहते हैं |
|
Answer» फोकस |
|
| 45135. |
The electric field at (30, 30) cm due to a charge of -8nC at the origin in NC^(-1) is |
|
Answer» `-400 (BAR(i) + bar(J))` |
|
| 45136. |
In the circuit shown, r = 4 Omega, C = 2mu F (a) Find the current coming out of the battery just after the switch is closed(b) Find charge on each capacitor in the steady state condition |
|
Answer» Solution :(a) Due to symmetry. the points of equal potential are joined together, and the circuit may be reducedas `R_(13)=(r)/(2)+(r)/(4)+(r)/(4)+(r)/(2)=(3)/(2)r` `Here,r=4Omega,R_(13)=(3)/(2)(4)=6omega` THUS,`I=(24)/(R_(13)=(24)/(6)=4A` (b) in the steady-state condition, the circuit may be reduced as,` R_(13) = 2r = 2(4)Omega = 8Omega` `I=(24)/(8)=3A``V_(56)=(2r)(1)/(2)=Ir=(3)(4)=12V` Equivalent capacitance between 5 and 6 is `C_(56)=(C)/(2)=1muF` `thereforeq1_(56)=C_(56)V_(56)=12muC` NOW,`V_(97)=V_(17)-V_(19)` `=-r(1)/(2)+2(rl)/(2)=(rl)/(2)=((4)(3))/(2)=6V` therefore`q_(97)=(2)(6)=12muC` Similarly, `q_(89) = 12muC` 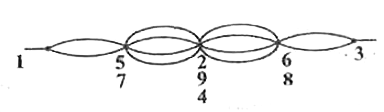 
|
|
| 45137. |
प्रथम 200 प्राकृत संख्याओं का योगफल है |
|
Answer» 303600 |
|
| 45138. |
An electromagnetic wave travels in xy plane making an angle theta with x-axis. Then the equation of the wave is |
|
Answer» `E=E_(0)sin(omegat-kxcos THETA+ky sin theta)` |
|
| 45139. |
If speed of electron emitted becomes double change in wavelength will be ……. |
|
Answer» increased by `(lambda)/(2)` Kinetic energy of electron `E_(1)=(1)/(2)mv_(1)^(2)` `E_(2)=(1)/(2)mv_(2)^(2)=(1)/(2)m(2v_(1))^(2)=(1)/(2)m(4v_(1)^(2))` `therefore E_(2)=4[(1)/(2)mv_(1)^(2)] therefore E_(2)=4E_(1)` Now `lambda=(h)/(sqrt(2ME))` `therefore lambda prop (1)/(sqrt(E))` `therefore (lambda_(2))/(lambda_(1))=sqrt((E_(1))/(E_(2)))=sqrt((E_(1))/(4E_(1)))=(1)/(2)therefore lambda_(2)=(lambda_(1))/(2)` `therefore` Decrease in wavelength `lambda_(1)-(lambda_(1))/(2)=(lambda_(1))/(2)`. |
|
| 45140. |
Light with an energy flux of 18 W//cm^(2) falls on a nonreflecting surface at normal incidence. If the surface has an area of 20 cm^(2), find the average force exerted on the surface during a 30 minute time span. |
|
Answer» Solution :The TOTAL energy falling on the surface is `U=(18 W//cm^(2))xx(20 cm^(2))xx(30xx60 s)` `=6.48 xx10^(5) J` Therefore, the total momentum DELIVERED (for complete absorption) is `p=(U)/(c )=(6.48xx10^(5) J)/(3xx10^(8) m//s)=2.16 xx10^(-3) kg m//s` The AVERAGE force exerted on the surface is `F=(p)/(t) =(2.16 xx10^(-3)/(0.18xx10^(4))=1.2xx10^(-6) N` How will your result be modified if the surface is a perfect reflector? |
|
| 45142. |
Write a note on radioactivity. |
|
Answer» Solution :LAW of radioactive decay : At any instant t , the number of decays per unit time, called rate of decay `((dN)/(dt))` is proportional to the number of nuclei (N) at the same instant. `(dN)/(dt) infty N` By introducing a proportionality constant, the relation can be written as `(dN)/(dt) = lambda N` Here proportionality constant `lambda` is called decay constant which is different for differentradioactive sample and the negative sign in the equation implies that the N is decreasing withtime. By rewriting the equation (1) we get `dN = lambda Ndt`...(2) Here dN represents the number of nuclei decaying in the interval dt. Let US assume that at time `t = 0` s, the number of nuclei PRESENT in the radioactive sample is `N_(0)`. By integratingthe equation (2), we can calculate the number of underdecayed nuclei N at any time t. From equation (2) we get, `(dN)/(N) = - lambda dt` ....(3) `int_(N_(0))^(N) (dN)/(N) = - int_(0)^(t) lambdadt` `[In N]_(N_(0))^(N) = - lambda t` `In [(N)/(N_(0))] = - lambdat` Taking exponentials on both SIES, we get `N = N_(0)e^(-lambda t)` ...(4) ` [Note : e^(Inx) = e^(y) Rightarrow x = e^(y)]`  Equation (4) is called the law of radioactive decay. Here N denotes the number of underdecayednuclei present at any time t and `N_(0)` denotes the number of nuclei at initial time t = 0. Note that the number of atoms is decreasing exponentially over the tie. This implies that the time taken for all the radioactive nuclei to decay will be infinite. Equation(4) is plotted. We can also define another useful quantity called activity (R) or decay rate whichnumber of nuclei decayed per second and it is denoted as `R = |(dN)/(dt)|` Note : that activity R is a positive quantity. From equation (4), we get `R = |(dN)/(dt)| = lambda N_(0)e^(-lambdat)` ....(5) `R = R_(0)e^(-lambdat)` ...(6) where `R_(0) = lambda N_(0)` The equation (6) is also equivalent to radioactive law of decay. Here `R_(0)` is the activity of thesample at `t = (0) ` and R is the activity of the sample at any time t. From equation(6), activityalso shows exponential decay behavior. The activity R also can be expressed in terms of number of undecayed atoms present at any time t, From equation(6), since `N = N_(0)e^(-lambdat)` wewrite ` R = lambda N`...(7) Equation (4) implies that the activity at any time t is equal to the product of decay constant and number of undecayed nuclei at the same time t. Since N decreases over time, R also decreases. |
|
| 45143. |
Standard atmosphere pressure is |
|
Answer» a)`76xx13.6xx980cm `of mercury |
|
| 45144. |
A student makes a short electromagnet by winding 200 turns of wire around a non conducting cylinder of diameter, d= 4 cm . A current of 5 A is passed through the wire . Find the magnetic dipole moment of the device x, xgt gt d , on its axis the magnetic field of the dipole is 4 mu T ? |
| Answer» Solution :Dipole MOMENT = m = NI A.] AXIAL line , `B = (mu_0 2M)/(4PI x^3)` | |
| 45145. |
A coil of wire of radius r has 600 turns and a self inductance of 108 mH. The self inductance of a coil with same radius and 500 turns is |
|
Answer» 80mH `L=(mu_(0)N^(2)pir)/2` `LpropN^(2)r` `L_(1)/L_(2)=(N_(1)/N_(2))^(2)(r_(1)/r_(2))` `implies (108)/(L_(2))=((600)/(500))^2((r)/(r))` `thereforeL_(2)=75mH.` |
|
| 45146. |
Hot wire ammeters and voltmeters can be used to measure : |
|
Answer» only ALTERNATING CURRENTS and voltages |
|
| 45147. |
A cylinder of radius r and length L is placed in a uniform electric field in such a way that its axis remains parallel to the electric field. The electric flux passing through the surface of cylinder is |
|
Answer» ZERO `=Eacostheta =EA cos90^(@)=0` |
|
| 45148. |
What changes in the current in the range below saturation will take place, if the electrodes of an ionization chamber are brought closer? How will the saturation current change? Plot the current-voltage characteristics for some inter-electrode distance d, and for d_(2)ltd_(1). Assume the other parametersto remain constant. |
Answer» 
|
|
| 45149. |
If r the distance from the centre of the earth, then what is the nature of the graph of gravitational acceleration versus r for point below the earth's surface? |
| Answer» SOLUTION :A straight line. (For R LESS than the radius of the Earth, g PROP r.) | |
| 45150. |
What is Dopper effect ? Obtainan expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest. |
|
Answer» Solution :Doppler effect `:` The apparent change in the frequency heard by the observer due to the relative motion between the observer and the SOURCE of sound is calleddopplerd effect. When a whistling railway engine APPROACHES an observer standing on the platform, the frequency of sound appears to increase. When it moves away the frequency appear to decrease.  Expression for apparent frequency when source is in motion and listener at rest `:` Let S = Source of sound O = Listener Let 'S' be the source, moving with a velocity `'upsilon_(s)'` to wards the stationary listener. The distance TRAVELLED by the source in time period `'T' = upsilon _(s). T ` Thereforethe successive compressions and rarefactions are drawn closer to listener. `:. ` Apparent wavelength ` lambda' = lambda - upsilon_(s) T `. `lambda' = lambda- ( upsilon_(s))/(v) [ :' v = (1)/(T)]` `= ( lambdav =- upsilon_(s))/( v)= (upsilon-upsilon_(s))/(v)``[ :' v = v lambda ]` If" v' " is apparent frequency heard by the listener. then `v'= (upsilon)/( lambda')`where `'upsilon'` is velocity of sound in air. `v' = (upsilon.v )/( upsilon-v_(s))` Therefore the apparent frequency is greater than the actual frequency . Similary , if the sourceis away from the stationary listener thenapparent frequency`v' = ( upsilon.v)/( upsilon+ upsilon_(s))` , which is less than the actual frequency. LIMITATION `:` Doppler effectis applicable when the VELOCITIES of the source and listener are much less than that of sound velocity. |
|
