Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 353. |
(a) State the law of conservation of energy. (b) Name two forms of mechanical energy. (c ) Give three examples on transformation of energy to show that solar energy provides different forms of energy. |
|
Answer» Solution :(b) Two forms of mechanical energy : Potential energy `E_(p)` and Kinetic energy `E_(k)`. (c ) (i) The sun.s heat evaporates moistures so that it falls back to the earth as rain. Hydroelectric power PLANTS harness the energy of moving water. (ii) The sun powers the air CURRENTS that cause the wind to blow. This wind energy is used in WINDMILLS to generate electricity. (III) Fossil FUELS are the transformation of solar energy. (iv) Solar energy can be converted into electric power through photovoltaic conversion. |
|
| 354. |
Suppose a boy is enjoying a ride on a marry-go-round which is moving with a constant speed of 10 m/s. It implies that the boy is: |
|
Answer» at rest |
|
| 355. |
How does change in velocity happen in uniform circular motion ? Due to change in speed / change in direction/ due to change in both speed and direction. |
|
Answer» |
|
| 356. |
You find your mass to be 42 kg on a weighing machine. Is your mass more or less than 42 kg ? |
| Answer» Solution :When we weigh our body an upward force acts on it. This upward for the buoyant force As a result the body GETS pushed slightly UPWARDS, causing the weighing machine to SHOW a reading less than the actual value. | |
| 357. |
Towards which electrode, do the canal rays deflect ? |
| Answer» | |
| 358. |
A force of 7 N acts on an object. The displacement is, say 8m in the direction of the force (Fig 11.3) Let us take it that the force acts on the object through the displacement. What is the work alone in this case? |
|
Answer» Solution :When a force F acts on an object to displa CE it through a distance S in its DIRECTION, then the work done W on the body by the force is given by : Work done = Force X displacement W = `F XX S`Where F = 7N S = 8m `:.` Work done = W = `7xx8 = 56` Nm = 56 J |
|
| 359. |
Complete the following sentence : Sound is produced by a .............. body. |
| Answer» SOLUTION :VIBRATING | |
| 360. |
The centre of gravity and the centre of buoyancy of a floating body, in stable equilibrium, (i) are always same. (ii) are always along a same vertical line. |
|
Answer» Only (i) is TRUE |
|
| 361. |
the bats can fly in the darkness of night without colliding with the other objects by emitting special sounds while flying. Which characteristic of sound is used by the bats to navigate? |
|
Answer» ultrasound |
|
| 362. |
A Solid weighs 50 gf in air and 44 gf when completely immersed in water. Calculate: (i) the upthrust, (ii) the volume of the solid, and (iii) the relative density of the solid. |
|
Answer» Solution :Given weight of solid in air `W_(1)=50gf` and weight of solid in water `W_(2)=44gf`. (i) Upthrust= LOSS in weight when immersed in water `=W_(1)-W_(2)=50-44=6gf` (II) Weight of water displaced = upthrust =6 gf SINCE density of water is `1 g cm^(-3)`, THEREFORE volume of water displasced `=6cm^(3)` But a solid displaces water equal to its own volume, therefore volume of solid `=6cm^(3)` (iii) R.D. of solid `=("Weight of solid air")/("Weight in air -Weight in water")` `=(W_(1))/(W_(1)-W_(2))=50/(40-44)=50/6=8.33` |
|
| 363. |
A stone is thrown vertically up from the tower of height 25m with a speed of 20 m/s What time does it take to reach the ground ? (g=10 m//s^(2)) |
|
Answer» Solution :Sign convention must be used to solve this problem. It is shown in figure. We consider the UPWARD direction as POSITIVE and downward direction as NEGATIVE with respect to a point of reference. In the above example the point of projection is considered as the point of reference. Then, u=20 m/s `a=g=-10 m//s^(2)` `s=h=-25 m` From equation of motion `s=ut + 1//2 at^(2)` `-25 =20 t-1//2 X 10 x t^(2)` `-25=20t -5 t^(2)` `-5=4t -t^(2)` `rArr t^(2)-4t-5=0` Solving this equation, We get, (t-5) (t+1)=0 t=5 or -1 t=5s |
|
| 364. |
(a) How many millimeter (mm) are there in a kilometer (km) ? (b) How much larger than a nanosecond (ns) is a millisecond (ms)? (c) A microwatt (muW) is what fraction of a kilowatt (kW)? (d) A gigaparsec (GPsc) is how many kiloparsec (kpsc)? (e) What fraction of a kilovolt (kV) is a millivolt (mV)? |
|
Answer» SOLUTION :(a) `10^(6)` (b) `10^(6)` (c) `10^(-9)` (d) `10^(6)` (d) `10^(6)` |
|
| 365. |
In your everyday life you come across a range of motions in which (a) acceleration is in the direction of motion. (b) acceleration is against the direction of motion. (c) acceleration is uniform. (d) acceleration is non-uniform. Can you identify one example each of the above type of motion ? |
|
Answer» Solution :(a) A vehicle moving ALONG a straight road. (b) A ball thrown upwards. (C) A ball falling freely from a CERTAIN height. (d) MOTION of a vehicle on road with traffic. |
|
| 366. |
What is sound and how is it produced ? |
|
Answer» |
|
| 367. |
A Sonar device on a submarine sends out a signal and receive an eeho 5s later. Calculate the speed of sound in water if the distance of the object from the submarine is 3625m. |
|
Answer»
Total distance travelled by the sonar waves during the transmission and RECEPTION in water `=2D`. VELOCITY of SOUND in water, `upsilon=2d//t=2xx3625//5=1450m//s`. |
|
| 368. |
A body moving with uniform acceleration travels 84 m in the first 6 s and 180 m in the next 5 s. Find : (a) the initial velocity, and (b) the acceleration of the body. |
|
Answer» Solution :Let u be the initial velocity and a be the ACCELERATION of the body. Given, `S_(1), = 84` m, `t_(1), = 6` s, `S_(2), = 84 + 180` = 264 m and `t_(2), = 6 + 5 = 11` s From relation `S = UT +(1)/(2) at^(2)` Distance travelled in 6 s. `84 = u xx6+(1)/(2) a xx (6)^(2)` or 6u +18 a = 84 or u +3a= 14 Distance travelled in 11 s . `264 =u xx11+(1)/(2) a xx (11)^(2)` or 11 u +`(121)/(2)a = 264` or u `+(11)/(2) a = 24` On solving eqns. (i) and (ii) . Initial velocity of body u = 2 `m s^(-1)` and acceleration ` a =4 m s^(-2)`. |
|
| 369. |
The drawing shows a ship 800 m from a cliff. A gun is fired on the ship. After 5 seconds the people at the front of the ship hear the sound of the gun again. (a) What is the name of this effect? (b) What happens to the sound at the cliff? (c) How far does the sound travel in 5 seconds? (d) Calculate the speed of sound. |
|
Answer» |
|
| 370. |
Explain the principle, construction and working of a DC motor. |
|
Answer» Solution :A motor is an electrical machine which CONVERTS electrical energy into mechanical enerry. The PRINCIPLE of WORKING of a DC motor according to Faraday.s laws of electromagnetic induction is that whenever a current carrying conductor is placed in a magnetic field, it experiences a mechanical force. The various parts of a DC motor are: Permanent magnets onboth sides of a coil which consists of carbon brush and commutator as shown in 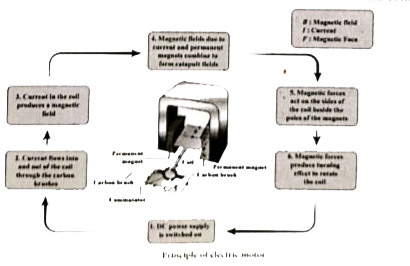 Working of electric motor is primarily dependent upon the interaction between magnetic field and current. The direction of this force is given by Fleming.s LEFT hand rule nad it.s magnitude is GIVNE by F=BIL. Where B = magnetic flux, density, I = current and L=length of the conductor withing the magnetic field. |
|
| 371. |
A train travels at a speed of 60 km h^(-1) for 0.5 h, 24 km h^(-1) for the next 0.25 h and then 72 kmh^(-1) for the next 0.75 h. Calculate the total distance covered by the train and its average speed. |
|
Answer» Solution :Average speed `= ("Distance")/("Time")` `therefore` Distance = Average SPEEC `xx` Time `= 60 km h ^(-1) xx 0.5 h = 30 km …(1)` `therefore ` Distance = Average speed `xx` Time `= 24 km h ^(-1) xx 0.25 h = 6 km …(2)` `therefore` Distance = Average speed `xx` Time `= 72 km h ^(-1) xx 0.75 h = 54 km ...(3)` From (1), (2) and (3), the total distance COVERED `= (30 + 6 + 54) km = 90 km` Total time take `= (0.5 + 0.25 + 0.75) h = 1. 50 h ` Average speed `= ("Total distance covered")/("Total time taken")= (90 km)/(1.50 h) = 60 km h ^(-1)` The total distance covered by the train `= 90 km.` |
|
| 372. |
When a cylindrical wooden piece weighing 75 gwt is made to float in water, 25% of the total volume of the water. Find the extra force in gwt required to be applied on the piece downwardsso that the piece gets immersed in water completely |
|
Answer» Solution :According to the law of floatation, weight of the floating body = weight of the LIQUID displaced `rArr("density of the body")/("density of the liquid")` `=("volume of the body inside liquid")/("total volume of the body")` Given `25%` of the body is above the water surface `rArr` FRACTION of the body inside water = `75%` `:.("Pwooden piece")/("Pwater")=75%` `rArr" Pwooden piece"=0.75" g cm"^(-3)` Given weight of the wooden piece = 75 gwt `:.` volume of the wooden piece `("75 gwt")/("0.75 g cm"^(-3))=100cm^(3)` volume of water displaced by the body = fraction of the body inside water X volume of the woodent piece `=0.75xx100=75cm^(3)` `:." remaining volume"=25cm^(3)` If the body has to be completely IMMERSED in water, the extra force required = weight of `25cm^(3)` of water = 25 gwt |
|
| 373. |
Two satellites of one metric ton and twelve metric tons masses are revolving around the Earth. The heights of these two satellites from the Earth are 1600 km and 25600 km, respectively. What is the ratio of their time periods and what is the ratio of the accelerations due to gravity at those heights? (Radius of the Earth = 6400km) |
|
Answer» Solution :(i) Find the radius of the Earth from the given DATA. Find the HEIGHTS of the two satellites from the Earth. What is Kepler's law of time periods ? Is `T^(2) prop R^(3)`? Find the RATIO of the time periods of the two satellites by the FORMULA `(T_(1)^(2))/(T_(2)^(2))=(r_(1)^(3))/(r_(2)^(3))` (ii) `T_(1) : T_(2) = 1 : 8` `g_(1) : g_(2) = 16 : 1` |
|
| 374. |
Find the height from the surface of the moon where the value of 'g' is equal to the value of 'g' at a height of 57,600 km from the surface of the Earth. (Take, mass of the Earth, M_(E) = 6 xx 10^(24) kg, Mass of the moon, M_(m) = 7.3 xx 10^(22) kg, radius of the Earth, R_(E) = 6400 and radius of the moon, R_(m) = 1740 km) |
|
Answer» Solution :(i) (1.) The VALUE of acceleration due to GRAVITY at a height 'h' is given by, `g^(1)` `= (GM_(m))/((R + h)^(2))` (2.) The value of `g^(1)` is equal height `h_(E)` from the SURFACE of the EARTH `h_(m)` from the surface of the moon. `rArr g^(1) = (GM_(E))/((R_(E) + h_(E))^(2)) = (GM_(m))/((R_(m) + h_(E))^(2))` Substitute the values of `M_(E), M_(m), R_(E), h_(E), R_(m)` and find the value of `h_(m)` from equation (2). (ii) 5300 km |
|
| 375. |
A simplependulumdesigned on themoon as aseconds pendulum istaken to a planet wheretheacceleration due to gravity on thesurfaceis twicethat on theEarth . If g_("earth") : g_("moon") =6 :1 find theperiodof oscillation of thependulum on theplanet mentionedabove. |
|
Answer» Solution :(i) Express1 m.s.din thedifferent portions ofthescale as a fraction of an INCH andconvertinto cm . Countthe totalnumber of divisions andconvert into cm toarrive at thelengthofobject in cm. Alternately FIND thelengthin inches and convert into cm (II) Countthenumberof M.S.D. 's fromleftblockto2 say x `1 M.S.D. =(1)/(16) inch` Countthe numberof M.S.D.'s from2 to rightblocksay y here ` 1 M.S.D.=(1)/(8)`inch Lengthof the object`=(x xx (1)/(16) +yxx(1)/(8) ) `inch `=((x+2y)/(16))` inch Convert this value tocm (III) 5.87 cm |
|
| 376. |
Name the instrument which can measure accurately the following the thickness of a paper |
| Answer» SOLUTION :SCREW GAUGE | |
| 377. |
The density of ice is 0.92gcm^(-3) and that of sea water is 1.025gcm^(-3) Find the total volume of an iceberg which floats with its volume 800cm^(3) above water. |
|
Answer» |
|
| 378. |
It is well known that there exists a gravitational force of attraction between the Earth and the sun. Then, why does the Earth not collide with the sun? Is it possible for three bodies of equal mass to be at rest relative to each other? Explain. |
| Answer» Solution :What is CENTRIPETAL and centrifugal FORCE? What are the directions of the forces of attraction possible for three bodies of EQUAL masses to be at rest relative to each other and revolving around a given centre. What is the DIRECTION of the net force acting on each mass? Will this net force produce centripetal force? | |
| 379. |
As the altitude from the surface of the Earth increases, the atmospheric temperature falls. Explain. |
|
Answer» Solution :Mass of substance, `(m)=0.1` kg The heat produced by COMBUSTION, (Q) = heat utilized in melting ice, `(Q_(1))`+ heat utilized in RAISING the temperature of water `(Q_(2))` `Q_(1)=(1 kig ) (336000 J kg^(-1))=3,36,000 J.` `Q_(2)=(1 kg) (4200 J kg^(-1)K^(-1)) (50 K) =210000 J`. `therefore Q=546 kJ` The calorific value of the substance `=(Q)/(m)=(546 kJ)/(0.1 kg)` `=5.46 MJ kg^(-1)` |
|
| 380. |
What is the full form of SI system? |
| Answer» SOLUTION :The FULL FORM of S . I . SYSTEM is International System of Units . | |
| 381. |
You have a block of a mystery material, 12 cm long, 11 cm wide and 3.5cm thick. Its mass is 1155 grams. (a) What is its density? (b ) Will it float in a tank of water, or sink? |
|
Answer» Solution :(a) `"Density" = "Mass"/"Volume" = (1155g)/(12 cm xx 11 cm xx 3.5 cm) = (1155g)/(462 cm^(3)) = 2.5 G cm^(-3)` (B)The mystery material is DENSER than the water, so it SINKS. |
|
| 382. |
A car travels with a uniform velocity of 20 m s^(-1) for 5 s. The brakes are then applied and the car is uniformly retarded. It comes to rest in further 8 s. Draw a graph of velocity against time. Use this graph to find : (i) the distance travelled in first 5 s, (ii) the distance travelled after the brakes are applied, (iii) total distance travelled, and (iv) acceleration during the first 5 s and last 8 s. |
Answer» Solution :The graph of VELOCITY against time is shown in FIG. 2.27.  m (i) The DISTANCE TRAVELLED in first 5 s = area of rectangle OABD = `OD xx OA = 5 s xx 20 m s^(-1) = 100 m` (ii) The distance travelled by car after the brakes are applied = area of `Delta BDC =(1)/(2)xxDCxxDB` `= (1)/(2) xx(13-5) s xx 20 m s^(-1) = 80 m`. (iii) Total distance travelled = area of rectangle OABD + area of triangle BDC = 100 + 80 = 180 m (iv) Acceleration in the first 5 s (in part AB) = 0 (since straight line AB is parallel to the time axis, so slope = 0). Acceleration in the last 8 s (in part BC) = Slope of the line BC `= (BD)/(DC) = ((0-20)m s^(-1))/((13-5)s)=(-20 m s^(-1))/(8 s )` `=- 2.5 m s^(-2)` Since acceleration is negative so retardation = `2.5 m s^(-2)` . |
|
| 383. |
The fundamental frequency of an open is 450 Hz and that of a closed pipe is 350 Hz . The two pipes are joined together to form a longer pipe . Find the fundamental frequency of this new pipe . Take velocity of sound are 330 m s^(-1). |
|
Answer» Solution :(i) SUM of lengths of open pipe and closed pipe gives length of longer pipe (ii) `n_(o) = (V)/(2 l_(o)) , n_(c) = (v)/(4l_(c))` `n_("long") = (v)/(4(l_(o) + l_(c)))` |
|
| 384. |
Essentially, a Coolidge tube is a discharge tube. How is it different from the Crookes tube used to study the cathode rays ? What is the function of the additional components? |
| Answer» | |
| 385. |
If the distance between two bodies that attract each other is trebled, how many times will their mutual force of attraction be? (9 time, 3 times, 1/3, 1/9) |
|
Answer» |
|
| 386. |
What is the wavelength of a sound wave in air at 20^(@)C with a frequency of 22 Mhz? |
|
Answer» SOLUTION :`lambda=v//n` Here, `v=344 MS^(-1)` `n=22MHz=22xx10^(6)Hz` `lambda=344//22xx10^(6)=15.64xx10^(-6)m=15.64 MU m`. |
|
| 387. |
A ball thrown up vertically returns to the thrower after 6s. (a) The velocity with which it was thrown up, The maximum height it reaches, and © Its position after 4s |
|
Answer» Solution :Time ascent is equal to the time of descent. The ball TAKES a total of 6s for its upward and downward journey. Hence, it has TAKEN 3s to attain the maximum height. Final velocity of the ball at THA maximum height, v=o. Acceleration due to gravity, `g=-9.8ms^(-2)` Equation of motion, v=u+gt will give `o=u+(-9.8xx3)` `u=9.8xx3=29.4ms^(-1)` Hence, the ball was thrown upwards with a velocity of `29.4ms^(-1)` Let the maximum height attained by the ball be .H. Initial velocity during the upward journey `u=29.4ms^(-1)` Final velocity, v=o Acceleration due to gravity, `g=-9.8ms^(-2)` From the equation of motion, `s=ut+1//2at^(2)` `h=29.4xx3+1//2xx-9.8xx(3)^(2)=44.1m` Ball attains the maximum height after 3s. After attaining this height will start falling downwards. In this case, Initial velocity u=o Position of the ball after 4s of the throw is given by the distance travelled by it during its downward journey is `4s-3s=1s`. Equation of motion, `s-ut+1//2g""t^(2)` will give. `S=Oxt+1//2xx9.8xx12=4.9m` Total height =44.1m This means that the ball is 39.2m (44.1m -4.9m) above the ground after 4 seconds. |
|
| 388. |
Speed of light in glass is 2xx 10^(8) ms^(-1) . Find the refractive index of glass. |
| Answer» Solution :`""_(a) mu_(G) = (3 XX 10^(8) )/(2 xx 10^(8) ) = (3)/(2) = 1.5` | |
| 389. |
A sound wave causes the density of air at a place to oscillate 1200 times in 2 minutes. Find the time period and frequency of the wave. |
|
Answer» Time PERIOD = ?Frequency `=1//T` `T=(1)/("Frequency")=1/10=0.1s` |
|
| 390. |
What is speed of light in vacuum? |
|
Answer» Solution :The speed of LIGHT in vacuum is known to be almost exactly 300,000 km per second. In 1665 the DANISH astronomer of Roemer first ESTIMATED the speed of light by observing ONE of the TWELVE moons of the planet Jupiter. |
|
| 391. |
A body of density rho sinks in a liquid of density rho_(L).The densities rho and rho_(L) are related as: |
|
Answer» `rho=rho_(L)` |
|
| 392. |
What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis ? |
| Answer» SOLUTION :The OBJECT MOVES with a UNIFORM SPEED. | |
| 393. |
The volume of a 500g sealed packet is 350cm^(3). Will the packet float or sink in water if the density. |
|
Answer» Solution :Density of the 500g SEALED packet = MASS of the packet/volume of the packer. `=500//350=1,428gcm^(-3)` The density of the SUBSTANCE is more than the density of water `(1gm^(-3))`. HENCE it will SINK in water. The mass of water displaced by the packet is equal to the volume of packet i.e., 350g. |
|
| 394. |
Compare approximately the speed of sound in air, water and steel |
| Answer» SOLUTION :`1:4:15` | |
| 395. |
A small stone of mass m(=200g) is held under water in a jar and is allowed to fall as shown in fig. the forces acting on stone are also shown. (i) What does F_(2) represent? (ii) What does m_(1) represent? (iii) What is the net force acting on stone? (iv) What is the acceleration of stone as it falls through water? Neglect the force due to viscosity. Assume that the volume of stone =80cm^(3), density of water =1.0gcm^(-3) and acceleration due to gravity g=10ms^(-2) |
|
Answer» Solution :(i) `F_(2)` represents the upthrust on STONE due to water. (ii) `m_(1)` represents the MASS of water displaced by stone (III) Net force acting on stone `=F_(1)-F_(2)` (downwards) (iv) Given `V=80cm^(3),rho=1 G cm^(-3), g=10ms^(-2)`, `m=200g=200/1000kg=0.2kg` `:.` weight of stone `F_(1)=mg=0.2kgxx10ms^(-2)=2N` Mass of water displaced `m_(1)=v rho =80xx1=80g` `=80/1000kg=0.08kg` upthrust `F_(2)=m_(1)g=0.08kgxx10ms^(-2)=0.8N` Hence net downward force on stone `=F_(1)-F_(2)` `=2-0.8=1.2N` `:.` ACCELERATION`=("Force")/("Mass")=(1.2N)/(0.2kg)=6m^(-2)` |
|
| 396. |
A conductor of length 50 cm carrying a current of 5A is placed perpendicular to a magnetic fieldof induction 2xx10^(-3) T. Find the force on the conductor. |
|
Answer» SOLUTION :Force on the conductro `=ILB` `=5x50xx10^(-2)xx2xx10^(-3)` `=5XX10^(-3)N` |
|
| 397. |
A car starting from rest, accelerates at a rate of 2 m s^(-2) for 5 s. For this journey, (a) draw the velocity-time graph (b) draw the displacementtime graph using the velocity-time graph in part (a). |
|
Answer» Solution :(a) Given, u = 0, a = 2 m `s^(-2)`. The velocity of car at different instants is given in the table below:  Fig . 2.30 SHOWS the velocity time graph.  (b) From Fig. 2.30, the displacement of car at any instant can be obtained by FINDING the area enclosed by the straight line with the time axis up to that instant. At t= 1 s, displacement `S= (1)/(2) xx1 xx2=1 ` m At t= 2 s, displacement `S= (1)/(2) xx2xx4 =4 `m At t=3, s displacement `S= (1)/(2) xx4xx8 = 16 m` At t = 4 displacement `S=(1)/(2)xx4xx8 = 16 m ` At t = 5 displacement `S= (1)/(2) XX5 xx10 = 25` m  The displacement time graph i show in Fig 2.31 
|
|
| 398. |
You are given two similar bars. One is a magnet and the other is of soft iron. How will you distinguish and identify them? |
| Answer» SOLUTION :A MAGNET when suspended FREELY will REST only in north-south direction, but soft iron bar will rest in any direction | |
| 399. |
In the figure shown below, cylinder A has pump piston, whereas B and C cylinder have lift pistons. If the maximum weight that can be placed on the pump piston is 50 kgwt, what is the maximum weight that can be lifted by piston in the cylinder B? Find the total mechanical adventage. ("Take g 10 m s"^(-2)). |
|
Answer» SOLUTION :Is the pressure exerted on cylinder 'A' (pump piston) equal to the pressure EXPERIENCED by lift pistons in B and C cylinders ? FIND the area of cross sections of the pistons in cylinders 'A' and 'B'. Then, find the pressure on the liquid in cylinder 'A' by `50" KG"_(wt)`. Use formula, `P=(F)/(A)`.(1) The same pressue is exerted on lift piston in cylinder 'B'. Find the maximum weight that can be lifted by the piston in the cylinder 'B' by using the formula, `W=PxxA=Pxxpi((1)/(4)m)^(2)`. (2) Put value of P from (1) into (2). Here, TOTAL mechanical advantage `=("Total load")/("Total effort")`. (3) Find the value of total mechanical advantage. |
|
| 400. |
The speeds of sound in four different media are given below. Which of the following is the most likely speed in m/s with which the two under water whales in a sea talk to each other when separated by a large distance? |
|
Answer» 340 |
|