Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

90001.

a. Describe the following giving linked chemical equations: (i) Cannizzaro reaction, (ii) Decarboxy lation. b. Complete the following chemical equations:

Answer»

Solution :a. Cannizzaro reaction: Aldehydes which do not have an `alpha`- hydrogen atom, undergo self concentrated alkali.
In this raction, one molecule of the aldehyde is REDUCED to ALCOHOL while another is oxidised to CARBOXYLIC acid salt.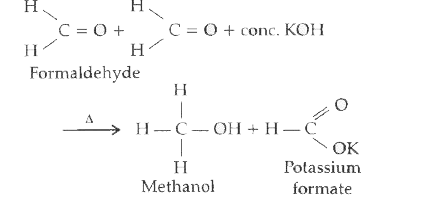

(ii) Decarboxylation: Carboxylic acid LOSE `CO_(2)` to form hydrocarbons when their sodium or potassium salts are heated with sodalime. The reaction is known as de-carboylation.
`R-COONa underset(Delta)overset(NaOH+CaO)(to) R -H+Na_(2)CO_(3)`
Discussion
90002.

(a) Describe the general trends in the following properties of the first series of the transition elements: (i) Stability of +2 oxidation state ""(ii) Formation of oxometal ions (b) Assign reason for each of the following: (i) Transition elements exhibit variable oxidation states. Transition metal ions are usually coloured

Answer»


SOLUTION :N//A
Discussion
90003.

(a) Describe the following characteristics of the first series (Sc to Zn) (i) Atomic radil, (ii) Oxidation states (iii) Ionisation enthalpies. (b) Name an important alloy which contains some of the lanthanoid metals. Mention its two uses.

Answer»

Solution :(a) (i) Atomic radii : From scandium to chromium atomic size decreases, increases in manganese and remains constant in Fe, Co, Ni, then increases in Cu and Zn.
The atomic radius decreases in a period in the begining because with INCREASE in atomic number, the nuclear charge goes on increasing progressively. The shielding effect of d-electrons is so small so that the net electrostatic attraction between the nuclear charge and the outermost e-increases consequently the atomic radius decreases, as the number of d-electrons increases. This neutralizes the effect of increased nuclear charge due to increase in atomic number and consequently atomic radius remain almost unchanged after chromium Towards the end of the series there is increased electron-electron replusion between the added electrons in the same orbital which exceed the attractive forces due to increased nuclear charge and their size increases.
(ii) Oxidation states: The transition elements exhibit a variety of oxidation states in their compounds. This is due to the fact that (n-1)d-orbitals are of comparable energy to rs orbitals and therefore some or all of the (n - 1)d electrons can be used along with as electrons in COMPOUND formation. Some common oxidation states exhibited by elements of first transition series are listed below: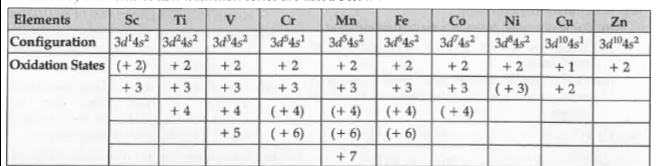

(The VALUES in parentheses are less common oxidation states)
(iii) Ionisation enthalpy. The ionisation enthalpy of transition elements lie between those of s-block and p-block elements. They are higher than those of s-block elements and lower than those of p-block elements.
(b) Lanthanoids find special use for the production of alloy steel for plates and pipes called misch metals. Misch metal CONTAINS lanthanoid metal (95%) + iron (5%) and traces of S, C, Ca, Al. It is used in magnesium based alloy to produce bullets, shells, lighter FLINT.
Discussion
90004.

(a) Describe electrophoresis with the help of a diagram. (b) What is meant by shape selective catalysis ? Give an example of shape selective catalyst.

Answer»

Solution :(a)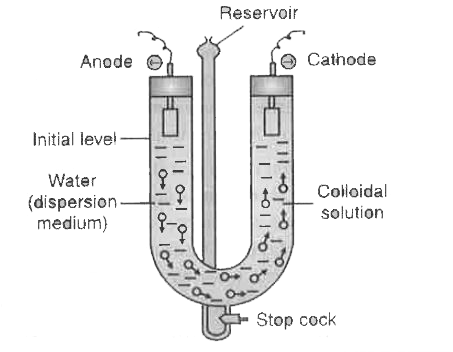
EXPLANATION : Movement of colloidal particles towards their oppositely charged electrode INDICATES that they are charged.
The catalytic reaction that depends upon the pore structure of the CATALYST and the size of the reactant and product molecules is called shape SELECTIVE CATALYSIS. Example : Zeolites
Discussion
90005.

Describe electrophoresis with the help of a diagram.

Answer»

SOLUTION : The movement of electrically charged colloidal particles towards either cathode or anode, under the influence of an electric field is CALLED electrophoresis.
For example : Arsenious SULPHIDE sol is TAKEN in a U-shaped tube, two platinum electrodes are dipped in it and an electric field is applied using a battery. The colloidal particles being negative, move to the positive electrode.
Discussion
90006.

(a) Derive the integrated rate equation for the rate constant of a first order reaction. (b) What is pseudo first order reaction?

Answer»

SOLUTION :(a) Consider a first order reaction,Rtoproducts.
Rate of reaction is given by.
`rate=(d[R])/([dt])=k[R]` where k is the rate constant.
on rearranging. `(d[R])/([R])=-K dt`
INTEGRATING both SIDES,
we get in [R] =- kt + L….(1)
where l is the constant of integration when time, `t = 0, [R] = [R]_(0)`, the equation becomes, `I = In [R]_(0)`,
substituting the value of I in equation (1), we have In`[R]=-kt+In[R]_(0)`
Rearranging the above equation,
In `[R]_(0) – In [R] = kt`
`K=(1)/(t)In ([R]_(0))/([R])`
`K=(2.303)/(t)"log"([R]_(0))/([R])`
(b) Order of reaction is ONE and molecularity is two or more than two are called pseudo first order reactions.
Discussion
90007.

(a) Derive the general form of the expression for the half-life of first order reaction. (b) The decomposition of NH_(3) on platinum surface is a zero order reaction. What are the rates of production of N_(2)" and "H_(2)" if "k=2.5xx10^(-4)" mol"^(-1)" L s"^(-1) ?

Answer»

Solution :`"["(b)(Delta[N_(2)])/(DELTAT)=2.5xx10^(-4)"MOL L"^(-1)s^(-1),(Delta[H_(2)])/(Deltat)=7.5xx10^(-9)"mol L"^(-1)s^(-1)"]"`
Discussion
90008.

Derive an integrated rate equation for the rate constant of a zero order reaction.

Answer»

Solution :(a) Consider a REACTION which is of zero order, `Rrarr P`
`Rate = -d[R]/dt = K[R]^(0) = -d[R]/dt = K`
`d[R] = -kdt`
integrating both sides we get,
`int d[R] = int-kdt`
[R] = -kt + 1
where, I is the constant of integration.
When t = 0, [R] = [R]0, where [R]0 is initial concentration of the REACTANT. Substituting in equation (i) we get,
`[R]0 = -k XX 0 + 1`
[R]0 = 1: Substituting the VALUE of I in equation (i), we get, `[R] = -kt + [R]^(0)`
`kt = [R]^(0) - [R]`
`k = ([R]^(0) - [R])/t`
(b)
Discussion
90009.

(a) Derive an integrated rate equation for the rate constant of a first order reaction.(b) The specific reaction rate of a reaction quadruples when temperature changes from 30^(0) to 50^(0).Calculate the energy of activation of the reaction.[Given:R = 8.314 JK^(-1)mol^(-1)].

Answer»

SOLUTION :(a)Consider a zero order reaction
`R to P`
`-d[R]/dt= -k.dt`
where k is the velocity constant of the FIRST order reaction
`-d[R]/[R]= -k.dt`
Integrating the equation
`intd[R]/[R] = -INT k.dt`
In[R]=-kt+I…..(1)
I is constant of integration when t=0 [R]=`[R]_(0)` where `[R]_(0)` is initial concentration of the reactant .
`In[R]_(0)= -Kxx0 +1`
I = `In[R]_(0)`
Substituting I in equation..(1)
`ln[R] = -kt + ln[R](0)`
`k=2.303/t log[R](0)/[R]`
(b)`logk_(2)/k_(1)=E_(a)/2.303 xx R[T_(2)-T_(1)/T_(1)xxT_(2)]`
`log4=E_(a)/2.303 xx 8.314[323-303/(303)(323)]`
`0.6021 = E_(a)/(2.303 xx 8.314) xx 20/303xx323`
`E_(a) = (0.6021 xx 2.303 xx 8.314 xx 303 xx 323)/20`
Discussion
90010.

The specific reaction rate of a reaction quadruples when temperature changes from 30°C to 50°C. Calculate the energy of activation of the reaction [Given : R = 8.314 "JK"^(-1) "mol"^(-1) ]

Answer»

<P>

Solution :(a) In first order reaction the rate of the reaction is proportional to first power of the concentration of the reactants.
Let us CONSIDER the FOLLOWING first order reaction :
`R to P`
The rate is given by :
`(-d[R])/(dt) prop [R]`
`(-d[R])/(dt) = k[R]`
where k is rate constant
`(-d[R])/([R]) =kdt`
multiply is given by -ve sign
`(d[R])/([R]) = - kdt`
on integration `int(d[R])/([R]) = -k int dt`
`In [R] = -kt + I`
Whent `t = 0, R = [R]_(0)`, where `[R]_0` = INITIAL concentration of the reactant
`:. [R]_(0) = -k(0) + I "" .......(1)`
`I = ln [R]_(0)`
Substituting the value of I in the above eqn,
`ln [R] = -kt + In [R]`
`kt = In[R]_0 - In [R]`
`kt-ln [R]_(0) - ln [R]`
`kt = ln ([R]_0)/([R])`
`k = 1/t ln ([R]_0)/([R])`
Changing into common log
`k = (2.303)/(t) "log" ([R]_0)/([R])"".........(2)`
(b) `"log" (k_2)/(k_1) = (E_a)/(2.303 R) [(T_2 - T_1)/(T_1T_2)]`
Given : `(k_2)/(k_1) = 4, T_1 = 30^@C = 30 + 273 = 303 K, T_2 = 50^@C = 50 + 273 = 273 = 323 K , R = 8.314 K^(-1) mol^(-1)`
`"log" 4 = (E_a)/(2.303 xx 8.314) [(323 - 303)/(303 xx 323)] `
`E_a = ("log " 4 xx 2.303 xx 8.314 xx 303 xx 323)/(20 ) = 56,414 J//mol = 56.414 KJ//mol` .
Discussion
90011.

Derive an integrated rate equation for rate constant of a zero order reaction.

Answer»

Solution :(a) `{:("LET us consider the following reaction which is of zero order."),(""R to P),("The rate is GIVEN by "),(""(-d[R])/(dt) = K[R]^(0)),(""(-d[R])/(dt) = k),(""-d[R] = kdt),(""d[r} = -kdt),("On integration"),(""int d[R] = -k int dt),(""[R] = -kt + I):}}......(i)`
`{:("Where , I is integration constant"),("When t = 0"),([R] = [R_0]"where " R_0 "is initial concentration of the reactant"),(""[R_0] = - k xx 0 + I),(""[R]_0 = I):}}`
`:. ` EQUATION (i) becomes
`{:([R] = -kt + [R]_(0)),(kt = [R]_(0) - [R]),(k = ([R]_(0) - [R])/(t)):}}.......(ii)`
(b) (i) `k = Ae (-E a)/(RT) ` OR Any other suitable form of equation.
(ii) `t_(1//2) = ([R]_(0)]/(2k)`.
Discussion
90012.

(a) Derive an integrated rate equation for rate constant of a zero order reaction. (b) Write (i) Arrhenius equation (ii) The formula to calculate half life period of zero order reaction.

Answer»

Solution :Consider a reaction, where `R to P`
Applying law of mass action
`r prop[R]^(@)`
`r=K[R]^(@)`But `r = -d[[R]]/(dt)`
`(-d[R])/(dt)=K[R]^(@) ,``[R]^(@) = 1`
`-d[R] = Kdt , d[R] = - Kdt.`
INTEGRATING on both sides
`intd[R]= - K int dt`
`[R] = -Kt+C .......(1)`
put `[R]=[R_(0)] and t=0`
`[R_(0)]= -K(0)+C`
`C=[R_(0)]`........... (2)
Substituting in eqn(1)
`[R] =-Kt + [R_(0)]`
`Kt=[R_(0)] - [R],`
`K=[[R_(0)]-[R]]/(t)`
(i) `K=Ae^((-Ea)/(RT))`
(ii) `t_(1/2)=[[R_(0)]]/(2K)`
Discussion
90013.

Derive an intergrated rate for the first order reaction.

Answer»

Solution :(a) Reaction in which the rate of the reaction is proportional to the first power of the concentration the reactant, R is called first order reaction.
For EXAMPLE : `R rarr P`
Rate `= -(d[R])/(d t) = k[R]`
`(d[R])/([R]) = -kdt`
Integrating the above EQUATION, ln [R] = -kt + I
Where I is the constant of integration
When t = 0, `R = [R]_(0)`
Where `[R]_(0)` is the initial concentration of the reactant
Therefore, equation (1) can be written as,
`ln[R]_(0) = k xx 0 + I`
`ln [R]_(0) = I`
Substituting the value of I in equation (1)
`ln [R] = kt + ln [R]_(0)`
Rearranging this equation
`ln.([R])/([R]_(0)) = -kt`
`k = (1)/(t)ln.([R]_(0))/([R])`
`k = (2.303)/(t)log.([R]_(0))/([R])`
(b) According to collision theory
(i) Reactant molecules most collide with sufficient kinetic energy known as activation energy or THRESHOLD energy.
(ii) Reactant molecules must collide with proper orientation.
(a) First order integrated rate equation :
`K = (2.303)/(t)log_(10).(a)((a-x))`
Where, K = rate constant
a = initial concentration
a - x = concentration at time (t).
t = time
x = concentration ion summed during time (t).
Derivation : For a reaction
`A rarr "products"`
A = reactant with initial concentration a.
Then, according to first order rate equation.
`(dx)/(d t) = K.d t`
On integration :
`int(dx)/((a-x)) = K int d t`
where, .C. is integration constant.
When `t = 0`
`C = -log_(e)a`.
Putting value of .C. in EQ. no. (2)
`-log_(e)(a-x) = Kt - log_(e)a`
Or, `log_(e)a - log_(e)(a-x) = Kt`
Or `K = (2.303)/(t)log_(10).(a)/((a-x))`
Discussion
90014.

According to collision theory, what are the two factors that lead to effective collisions

Answer»

SOLUTION :(a) Reaction in which the rate of the reaction is proportional to the first power of the concentration the reactant, R is called first order reaction.
For example : `R rarr P`
Rate `= -(d[R])/(d t) = k[R]`
`(d[R])/([R]) = -kdt`
Integrating the above equation, LN [R] = -kt + I
Where I is the constant of integration
When t = 0, `R = [R]_(0)`
Where `[R]_(0)` is the initial concentration of the reactant
Therefore, equation (1) can be written as,
`ln[R]_(0) = k xx 0 + I`
`ln [R]_(0) = I`
Substituting the value of I in equation (1)
`ln [R] = kt + ln [R]_(0)`
Rearranging this equation
`ln.([R])/([R]_(0)) = -kt`
`k = (1)/(t)ln.([R]_(0))/([R])`
`k = (2.303)/(t)log.([R]_(0))/([R])`
(b) According to collision theory
(i) Reactant molecules most collide with sufficient kinetic energy known as activation energy or threshold energy.
(ii) Reactant molecules must collide with proper orientation.
(a) First order integrated rate equation :
`K = (2.303)/(t)log_(10).(a)((a-x))`
Where, K = rate constant
a = initial concentration
a - x = concentration at TIME (t).
t = time
x = concentration ion summed during time (t).
Derivation : For a reaction
`A rarr "PRODUCTS"`
A = reactant with initial concentration a.
Then, according to first order rate equation.
`(dx)/(d t) = K.d t`
On integration :
`int(dx)/((a-x)) = K int d t`
where, .C. is integration constant.
When `t = 0`
`C = -log_(e)a`.
Putting value of .C. in eq. no. (2)
`-log_(e)(a-x) = Kt - log_(e)a`
Or, `log_(e)a - log_(e)(a-x) = Kt`
Or `K = (2.303)/(t)log_(10).(a)/((a-x))`
Discussion
90015.

What is the effect of positive catalyst on the energy of activation?

Answer»

SOLUTION :(a) Consider a first order reaction RTOP Rate = `-d[R]/dt=k[R](d[R])/[r]`=-kdt
Integrating the above equation In[R] =-kt +1
When t = 0, [R] = [R]
Equation (1) becomes In[R] = 1 Therefore equation (1) becomes
in[r]=-kt+in[R]
`k=1/(t) In[R]/[R] `
`k= 2.303/(t) “LOG” [R]_(0)/[R]`
(b) Energy of activation decreases
Discussion
90016.

(a) Derive a relationship between relative lowering of vapour pressure and mole fraction of thevolatile liquid. (b) (i) Benzoic acid completely dimerises in benzene. What will be vapour pressure of a solutioncontaining 61 g of benzoic acid per 500 g of benzene when the vapour pressure of purebenzene at the temperature of experiment is 66.6 torr ? (ii) What would have been the vapour pressure in the absence of dimerisation ? (iii) Derive a relationship between mole fraction and vapour pressure of a component of an ideal solution in the liquid phase and vapour phase.

Answer»

SOLUTION :64.19 TORR
Discussion
90017.

Derive an expression for half life period of a first order reaction.

Answer»

Solution :We know that
`K=(2.303)/(t)log_(10)""([R]_(0))/([R])"…(1)"`
where, K = Rate constant t = TIME
`[R]_(0)=` Initial concentration
`[R]=` Concentration at any time
`"when"t=t_(1//2)" then"[R]=([R]_(0))/(2)`
Substitute these values in equation (1) we get
`K=(2.303)/(t_(1//2))LOG""(cancel([R]_(0)))/(cancel([R_(0)]_(0))/(2))`
`K=(2.303)/(t_(1//2))log2"[log 2 = 0.3010]"`
`K=(2.303)/(t_(1//2))xx0.3010`
`K=(0.693)/(t_(1//2))""rArr t_(1//2)=(0.693)/(K)`
For the FIRST order reaction, half life periodis independent of initial concentration of the reactants
i.e., `t_(1//2)alpha(0.693)/(K)`
Discussion
90018.

(a) Derive a relationship between molality & molarity of a solution in which w g of solute of molar mass M g/mol is dissolved in W g solvent & density of resulting solution = 'd' g/ml. (b) Calculate molality of 1.2 M H_2SO_4 solution ? If its rho = 1.4 g/mL

Answer»

Solution :(a)SAY 1 L solution taken,
mass of 1 LIT solution = (1000 d) g
moles of solute = (molarity)
mass of solute = (molarity) `xx` m
mass of solvent = W = 1000 d – (molarity) `xx` m
`:.``"molarity"=(("molarity")xx1000)/(1000d-"molarity"xxM.Wt)`
[Where no.of moles of solute = molarity]
(B)`"Molarity"=(1.2xx1000)/(1000xx1.4-1.2xx98)=0.936`
Discussion
90019.

A depolarizer used is dry batteries is

Answer»

KOH
`NH_2OH`
`MnO_2`
`Na_3PO_4`

ANSWER :C
Discussion
90020.

A depolarizer used in dry cell batteries is

Answer»

Ammonium chloride
Manganese dioxide
Potassium hydroxide
Sodium phosphate

Solution :`MnO_(2)` is used in DRY BATTERIES CELL.
Discussion
90021.

A depolariser chloride

Answer»

Sodium Carbonate
Lead SULPHATE
Manganese DIOXIDE
NONE ofthese

Solution :D epolarimer used indry cell is MAGNESE dioxide `(MnO_(2))`.
Discussion
90022.

A depolariser used in dry cell batteries is :

Answer»

A mmonium chloride
Managanese dioxide
Potassium hydroxide
Sodium phosphate

Answer :B
Discussion
90023.

(A) Density of nitrogen obtained in chemical methods is more than that nitrogen separated from liquid air(R) Density of atmospheric nitrogen is different than expected mainly because of water vapour.

Answer»

Both (A) and (R) are true and (R) is the CORRECT EXPLANATION of (A)
Both (A) and (R) are true and (R) is not the correct explanation of (A)
(A) is true but (R) is false
Both (A) and (R) are false

Answer :D
Discussion
90024.

A dental disease characterised by mottling of teeth is due to presence of a certain chemical clement in drinking water.Which is that element

Answer»

Boron
Chlorine
Fluorine
Mercury

Solution :The excess of fluorine in water CAUSES fluorosis. The symptoms of fluorosis are motting of teeth (YELLOWISH streaks ) and ABNORMAL bones LIABLE to FRACTURE etc. It is an example of endemic disease.
Discussion
90025.

A delta is formed at the meeting point of sea water and river water. Why ?

Answer»

SOLUTION :River water is a COLLOIDAL solution of clay. Sea water CONTAINS a number of electrolytes. When river water MEETS sea water, the electrolytes in sea water coagulate the colloidal solution of clay RESULTING in deposition with the formation of delta.
Discussion
90026.

(A): Dehydration of alcohols can be carried out with conc H_(2)SO_(4) but not with conc. HCI. (R): H_(2)SO_(4) is dibasic while HCl is monobasic.

Answer»

Both A & Rare TRUE, R is the correct EXPLANATION of A
Both A & Rare true, R is not correct explanation of A
A is true, R is FALSE
A is false, R is true

Answer :B
Discussion
90027.

A definite volume of H_(2)O_(2) under going spontaneous decomposition required 22.8 cc. of standard permanganate solution for titration. After 10 and 20 minutes respectively the volumes of permanganate required were 13.8 and 8.25 c.c. (a) Find order of reaction. How many the result be explained ? (b) Calculate the time required for the decomposition to be half completed. (c) Calculate the fraction of H_(2)O_(2) decomposed after 25 minutes.

Answer»

SOLUTION :(a) first order, (B) 13.75 minutes, (C ) 0.716
Discussion
90028.

A degenerate gas is

Answer»

He
He I
He II
`._(2)^(3)He`.

ANSWER :C
Discussion
90029.

(a) Define the term 'chemotherapy'. (b) While antacids and anti allergic drugs interfere with the function of histamines, why do these not interfere with the function of each other?

Answer»

Solution :(a) Chemotherapy : The branch of chemistry which deals with the treatment of diseases using suitable chemicals is known as chemotherapy.
(b) Drugs designed to cure some ailment in ONE organ in the body do not affect the other because they work in different receptors. For example, secretion of histamine CAUSES allergy as WELL as acidity in stomach. Since anti allergic and ANTACID drugs work on different receptors, THEREFORE, antihistamines cure allergy while antacids remove acidity.
Discussion
90030.

Howthe weak and strong electrolytes are distinguished?

Answer»

Solution :(a) Weak ELECTROLYTE : The substance which partially ionized in solution is known as weak electrolyte. Example : `NH_(4)OH.`
STRONG electrolyte : The substance which completely ionized in solution is known as strong electrolyte. Example : `NACL`.
Discussion
90031.

(a) Define the following terms : {:((i)"Ideal solution",(ii)"Osmitic pressure"):} (b) Calculate the boiling point elevation for a solution prepared by adding 10g CaCl_(2) to 200g of water, assuming that CaCl_(2) is completely dissociated. (K_(b)"for water"=0.512Kg mol^(-1),"Mole mass of "CaCl_(2)=111g mol^(-1))

Answer»

Solution :(a) (i)Ideal solution : An idealsolution of the components A and B is defined as the solution in which the intermolecular interactions between A-B are of the same magnitude as theintermolecular interactions found in the pure coponent (A-A and B-B). Example: Benzene + Toluene
(ii) OSMOTIC Pressure : The minimum execess pressure that has to be applied on the solution to prevent the entry of the solvent into the solution through the semipermeable membrane is CALLED the osmotic pressure.
(b) `DeltaT_(b)=K_(b)m`
`T_(S)-T_(A)^(@)K_(b)xx(wB)/(M_(B)xxwA(kg))`
`T_(A)^(@)=100^(@)C`
`{:(w_(B)=10g,M_(B)=111g//mol),(w_(A)=10g,K_(b)=0.512kg//mol):}`
As, `CaCl toCa^(2+)+2CL^(-)`
i = 3 [Completely DISSOCIATES]
`T_(S)-T_(A)^(@)=ixx(Kfxxw_(B))/(M_(B)xxw_(A)(kg))`
`T_(S)100=(3xx0.512xx10^(5)xx1000)/(111xx200)=0.692`
`T_(S)=100.692^(@)C`
Discussion
90032.

(a) Define the following terms : (i) Molarity (ii) Molal elevation constant (K_(b)) (b)A solution containing 15 g urea (molar mass = 60 g mol^(-1)) per litre of solution in water has same osmotic pressure (isotonic) as a solution of glucose (molar mass = 180 g mol^(-1)) in water. Calculate the mass of glucose present in one litte of its solution.

Answer»

Solution :(a) (i) Molarity is defined as NUMBER of moles of solute dissolved in one litre of solution.
(ii) lt is equal to elevation in boiling point of 1 molal solution.
(b) For ISOTONIC solutions :
`pi_("urea") = pi_("glucose")` `(W_("urea"))/(M_("urea" xx V_(S)))= (W_("Glucose"))/(M_("Glucose" xx V_(s)))`
(As volume of solution is same
`(W_("urea"))/(M_("urea")) = ("glocose")/("glocose")`
or `(15 g)/( 60 g" mol"^(-1)) = (w_("Glucose"))/(180 g "mol"^(-1))`
`W_("glucose")= (15 g xx 180 g "mol"^(-1))/(60 g "mol"^(-1))`= 45 g
Discussion
90033.

(a) Define the following terms: (i) Limiting molar conductivity (ii) Fuel cell. (b) Resistance of a conductivity cell filled with 0.1 mol L^-1 KCl solution is 100 Omega. IF the resistance of the same cell when filled with 0.02 mol L^-1 KClsolution is 520 Omega, calculate the conductivity and molar conductivity of 0.02 mol L^-1 KCl solution. The conductivity of 0.1 mol L^-1 KCl solution is 1.29 times 10^-2 Omega^-1 cm^-1.

Answer»

Solution :(a) (i) Limiting molar conductivity: When concentration approaches zero the conductivity is known as limiting molar CONDUCITIVITY.
(ii) Fuel cell: A fuel cells which convert the energy of COMBUSTION of fuels to electrical energy.(b) Given, cell constant =`G^@`
`= conductivity times Resistance `
`thereforeG^@=1.29S//m times 100 OMEGA`
`=129 m^-1=1.29 cm^-1`
Conductivity of `0.02 mol L^-1`, KCl solution = cell constant/resistance
`K=G^*/R=(129 m^-1)/(520 Omega)=0.248 S m^-1`
`=0.248 times 10^-2 Scm^-1`
Concentration =`0.02 mol L^-1`
`=1000 times 0.2 mol m^-3`
`=20 mol m^-3`
Molar conductivity =`A_m=K/C`
`=(248 times 10^-3 Sm^-1)/(20 mol m^-3)`
`=124 times 10^-4 S m^2 mol^-1`
`=124 S cm^2 mol^-1`
Discussion
90034.

(a) Define the following terms : (i) Ideal solution (ii) Azeotrope (iii) Osmotic pressure (b) A solution of glucose (C_(6)H_(12)O_(6)) in water is labelled as 10% by weight. What would be the molality of the solution? (Molar mass of glucose= 180 g mol^(-1))

Answer»

Solution :(a) (i) Ideal Solution : The solutions which OBEY raoult' s law over the entire range of concentration are known as ideal solution.eg-n-hexane and n-heptan
`DeltaH(mix)=0, Delta.V (mix)=0`
(ii) AZEOTROPE : These are constant boiling mhtures which dishll out unchanged in their composition eg. ethanol and water.
(iii) Osmotic pressur: It is extra PRESSURE which is applied on the solution to just prevent the FLOW of solvent into the solution through a semi permeable membrane
(b) 10% by weight : 10 gm of glucose in 100 gm of solution
`therefore""WB=10gm, WA=90g, m ws = 100g`
`MB(C_(6)H_(12)O_(6))=180 g`
`"MOLALITY (m)"=(WB)/(MBxxWA(kg))=(10xx1000)/(180xx90)=0.617 m`
Discussion
90035.

(a) Define the following terms : (i) Ideal solution (ii) Azeotrope (iii) Osmotic pressure (b) A solution of glucose (C_(6)H_(12)O_(6))in water is labelled as 10% by weight. What would be the molality of the solution ? (Molar mass of glucose = 180 g mol^(-1))

Answer»

SOLUTION :(a) (i) IDEAL solution : Refer S.A. T.Q. 7 (ii).
(ii) Azeotrope : A liquid mixture which distills at constant temperature without under going any changes in composition is called Azeotrope.
(iii) Osmotic presslll.e : Refer V.S.A.T.Q. 2. (b) Given MOLECULAR mass of glucose = 180 G `mol^(-1)` % by weight = 10%
`m=(100-WT%)/((100-wt%)xx"molecular wt. solute")`
or `m = (wxx1000)/(MxxW)`
`m=(1000xx10)/((100-10)xx180)`
`=(1000)/(90xx180)`
m = 0.617 m
Discussion
90036.

Answer any three of the following questions. b. What is Peptisation ? Give an Example

Answer»

Solution :(a) The catalytic reaction that depends upon the PORE STRUCTURE of the catalyst and the size of the reactant and product molecules is called shape selective catalysis. ZSM-5
(b) The process of conversion of precipitate (FRESHLY prepared) into colloidal sol by the addition of small amount electrolyte (which have a common ion of the precipitate).
Example: When a freshly prepared ferric hydroxide ppt is treated with ferric chloride electrolyte, it gives ferric hydroxide sol. Any one OR Any other suitable example
(c) `x/m = k p^(1//n)` Detailed Answer:
(c) It gave an empirical relation between the quantity of gas adsorbed by unit MASS of solid adsorbent and pressure at a particular TEMPERATURE. It is given by the equation:
`x/m = k.p^(1/n)`
where, x is the mass of the gas adsorbed on mass m of the adsorbent at pressure p. k and n are constants which depend on the nature of the adsorbent and the gas at a particular temperature,
Discussion
90037.

Answer any three of the following questions. a. Define Shape Selective catalysis. Name the Zeolite Catalyst used to convert alcohols to gasoline in petroleum industry

Answer»

Solution :(b) Zeolite CATALYST is ZSM -5.
(b)The process of conversion of freshly prepared precipitate into a colloidal solution by adding an electrolyte containing the common ion is called peptisation.
Example: Ferric hydroxide SOL `[Fe(OH)_(3)]`,
is prepared by adding ferric chloride to freshly prepared precipitate of `Fe(OH)_(3)`.
(C) `X/m=K.p^(1/(n))`
x is MASS of the gas adsorbed.
m is mass of the adsorbent.
p is pressure.
`K_(1)` and n are constants.
Discussion
90038.

(a) Define ligand. (b) Give two examples for monodentate and bidentate ligands.

Answer»

Solution :Ligand. It is an atom or ion or molecule which can donate at least one lone pair of electron to a metal atom/ion forming coordinate BOND.
MONODENTATE LIGANDS : `F^(-),H_(2)O`
Bidenate ligands :
Ethylene diamine `""` Oxalate
`UNDERSET(CH_(2)-NH_(2)) underset(|)(CH_(2)-NH_(2)) underset(O= C-O^(Ɵ)) underset(|)(O=C-O^(Ɵ))`
Discussion
90039.

(a) Define peptisation. (b) Explain why bleeding is stopped when alum is applied on a fresh cut.

Answer»
Discussion
90040.

(a) Define molar conductivity of a solution and explain how molar conductivity changes with change in concentration of solution for a weak and a strong electrolyte. (b) The resistance of a conductivity cell containing 0.001 M KCl solution at 298 K is 1500 Omega.What is the cell constant if the conductivity of 0.001 M KCl solution at 298 K is 0.146 xx 10^(-3) S cm^(-1)?

Answer»

Solution :(a) MOLAR conductivity is the conductivity of all the ions produced by ionisation of 1 G mol of an electrolyte when present in V mL of solution. It is denoted by `Lambda_(m)`.
where V = volume in mL containing 1 g mol of the electrolyte
`Lambda_(m) = k xx 1000/C`
where C = concentration of the solution in g mol/L.
Variation of molar conductivity with concentration for strong electrolytes - Molar conductivity increases slowly with dilution. It approaches a limiting value when the concentration approaches zero. This value is called molar conductivity at infinite dilution `Lambda_(m)^(@)`. Variation of conductivity with concentration may be given by:
`Lambda_(m)= Lambda_(m)^(@) =AC^(1//2)`, where A is a constant and C is concentration.
Variation of molar conductivity with concentration for weak electrolytes - Variation of `Lambda_(m)`with concentration is very large to the EXTENT that we cannot obtain molar conductance at infinite dilution `Lambda_(m)^(@)`by extrapolation of `Lambda_(m)` VS `C^(1//2)` plots.
(b) Conductivity `K = 0.146 xx 10^(-3) S cm^(-1)`
Resistance = R= 1500 ohm
Cell constant = Conductivity (k) `xx` Resistance (R)
`=0.146 xx 10^(-3) S cm^(-1) xx 1500 Omega`
`=0.219 cm^(-1)`
Discussion
90041.

(a) Define Ideal and Non-ideal solutions and give one example of each. (b) Define Henry's law. Give two applications of Henry's law.

Answer»

Solution :(a) Ideal solution. A solution is said to be ideal if it satisfies the following conditions : (i) It obeys Raoult.s law at all temperatures and concentrations.
(ii) `Delta V_("(mix)") = 0 `
(ii) `Delta H_("(mix)") = 0`
For example, Benzene + Toluene
Non-ideal solution. A solution is said to be non-ideal if (i) it does not obey Raoult.s law at all temperatures and concentrations.
(ii) `Delta V_(" (mix)")ne0 `
(iii) `Delta H_("( mix)")ne0`
For example, Water + ETHYL alcohol
(b) Henry.s law. It states that the MASS of the gas (m) dissolved in a given volume of the liquid at constant temperature is directly proportional to the pressure (P) of the gas in equilibrium with the liquid.
`m prop P`
(i) In preparing soda water drinks, carbon dioxide is dissolved in water under pressure and BOTTLE is SEALED under pressure.
(ii) Deep divers use cylinder CONTAINING `O_2, N_2,` and He for respiration. ·
Discussion
90042.

(a) Define electrode potential.

Answer»

Solution :(a) For ANSWER, consult SECTION 4.
(b) For answer, consult section 5.
Discussion
90043.

(a) Define coagulation or flocculation. (b) What is the difference between lyophilic and lyophobic sols ?

Answer»
Discussion
90044.

(A) Decomposition of Ammonia on platinum surface at high pressure is a zero order reaction (R ) At high pressure, metal surface gets saturated with gas molecules

Answer»

Both (A) and (R ) are TRUE and (R ) is the CORRECT explanation of (A)
Both (A) and (R ) are true and (R ) is not the correct explanation of (A)
(A) is true but (R ) is false
Both (A) and (R ) are false

Answer :A
Discussion
90045.

(A) Deep sea divers use helium-oxygen mixture for respiration(R) Unlike nitrogen, helium is not soluble in blood even under high pressure.

Answer»

Both (A) and (R) are true and (R) is the CORRECT EXPLANATION of (A)
Both (A) and (R) are true and (R) is not the correct explanation of (A)
(A) is true but (R) is false
Both (A) and (R) are false

Answer :A
Discussion
90046.

(a) Deficiency of which vitamin leads to night blindness? (b) Which hormone is responsible for the hyperthyroidism? (c) What is a Zwitter ion of an amino acid? Give its general formula.(d) What is a nucleotide?

Answer»

Solution :(a) Vitamin A(b) Thyroxin
(c) The AMINO ACID forms dipolar ION called ZWITTER ion in aqueous solution.
(d) Basic unit of NUCLEI acid containing one sugar unit, heterocyclic base and phosphoric acid. is called nucleotide.
Discussion
90047.

A decinormal calomel electrode contains

Answer»

N/10 SOLUTION of `Hg_(2) Cl_(2)`
1 N solution of HCl
1 N solution of `Hg_(2) Cl_(2)`
N/10 solution of KCL

Solution :DECINORMAL i.e.` (N)/(10)` KCl solution .
Discussion
90048.

A decimolar solution of potassium ferrocyanide K_4Fe(CN)_6is 50% dissociated at 300 K. Calculate the value of van't Hoff factor for potassium ferrocyanide.

Answer»

SOLUTION :`ALPHA = 50% = 0.50`
`i= 1+ 2 alpha`
`=1 + (2 xx 0.50) = 1 + 1 = 2 `
Discussion
90049.

A decimolar solution of potassium ferrocyanide is 50% dissociated at 300K. Calculate the osmotic pressure of the solution. (R="8.314 J K"^(-1)"mol"^(-1)).

Answer»


SOLUTION :`{:(K_(4)[FE(CN)_(6)],hArr,4K^(+),+,[Fe(CN)_(6)]^(4-),),(1-alpha,,4alpha,,""alpha.,"TOTAL "=1+4alpha):}`
`i=1+4alpha=1+4xx0.5=3`
Apply `pi=iCRT`
Discussion
90050.

A decimolar solution of potassium ferrocyanlde K_(4) [Fe(CN)_(6)] is 50% dissociated at 3001K. Calculate the value of Van't Hoff factor for postuslum ferrocyanide.

Answer»

Solution :Vant HOFF factor `"" (i) = ("Normal MOLAR MASS ")/("Abnormal molar mass") `
`alpha = (i-1)/(n-1)`
`(50)/(100) = (i-1)/(5-1)`
`i-1 = 4 XX 0.5 `
`i-1 = 2`
i=3
Discussion