94420 + Interview Questions in Chemistry in Class 12 Page 1803 InterviewSolution

90101.	A current of 9.65 ampere folwing for 10 minute depostits 3.0 g of a metal. The equivalent weight of the metal is :
Answer» 10 30 50 `96.5` ANSWER :C

Discussion

90102.	A current of 9.65ampere flowing for 10 minutes deposits 3.0g of the metal which is monovalent. The atomic mass of the metal is:
Answer» 10 u 50 u 30 u `96.5` u Answer :B

Discussion

90103.	A Current of 9.65 ampere flowing for 10 minutes deposits 3.0g of themetal which is monovalent. The atomci mass of the metal is
Answer» 10 g 30 g 50 g 96.5 g Answer :C

Discussion

90104.	A current of 9.65 A is passed for 3 hours between nickel electrodes in 0.5 L of a 2 M solution of Ni(NO_3)_2. The molarity of the solution after electrolysis would be
Answer» 0.46 M 0.625 M 0.92 M 1.25 M Solution :`Q=9.65 xx 3 xx60 xx60 = 104220 C` `Ni^(@)+2e^(-) rarr Ni` `2 xx 96500 C` deposit 1 mole of `Ni^(2+)` `THEREFORE 104220 C` will deposit `Ni^(2+)` `(1)/(2 xx96500) xx 104220 = 0.54 ` mole ORIGINALLY 0.5 L of 2M sol. Contains `Ni^(2+)` =1 mole. Now 0.5 L will contain `Ni^(2+) =1 -0.54 =0.46` mole Hence, molarity = 0.92 mol `L^(-1)`

Discussion

90105.	A current of 9.65 A is passed for 3 hours between platinum electrodes immersed in 0.5 dm^(3) solutionof concentration 2 mol dm^(-3) Ni(NO_3)_2. The molarity of solution after electrolysis would be
Answer» 0.46 M 0.91 M `1.25M ` `0.625 M` Solution :`96500 to(1)/(2), 9.65 XX 3 xx 60 xx 60 to n =?` ` n =0.54 ` LIBERATED , `[Ni^(+2)]_("new") = ((1-0.54))/(0.5) = 0.92 M`

Discussion

90106.	A current of 96.5 A is passed for 18 min between nickel electrodes in 500 ml solution of 2 M Ni(NO_3)_2. The molarity of solution after electrolysis would be
Answer» 0.46 M 0.92 M 0.625 M 1.25 M Solution :Moles of `NI(NO_(3))_(2)` in 500 mL of 2M `Ni(NO_(3))_(2)` is `=(2xx500)/(1000)=1` MOL Charge `=96.5xx18xx60=104220C` `Ni^(2+)+2e^(-)toNi` `2xx96500`C deposits 1 mol of `Ni(NO_(3))_(2)` `therefore104220C` will DEPOSIT=`(104220)/(2xx96500)=0.54mol` so, moles `Ni(NO_(3))_(2)` LEFT `=1.0-0.54=0.46`mol Thus, molarity of `Ni(NO_(3))_(2)` solution `=2xx0.46=0.92mol//l`

Discussion

90107.	A currentof 6 amperesis passedthroughA1C1_(3) solutionfor 15 minutesusingPtelectrodes , when0.50 g A1 isproduced.Whatis the molarmass of A1 ?
Answer» Solution :Given : Electriccurrent= I =6 A TIME= t=15 min= 155 `xx 60 s = 900 s` Massof A1 produced = 0.504 g Molarmassof A1 = ? Reductionhalfreaction `A1_((ag))^(3)+ 3E^(-) to A1_((aq))` Quantityof electricitypassed= Q = `I xx t` `=6xx 900 = 5400 C` Number a of molesof electrons `= (Q)/(F ) =(5400)/( 96500) = 0.05596mol` Fromhalfreaction :'3 moles of electronsdeposit1 MOLE A1 `:. 0.05596 ` molesof electronswilldeposit `(0.05596)/(3) =0.01865mol A1 ` Now `:' 0.01865 ` mol A1weighs0.504 g `:.1 ` moleA1 willweigh ,` (0.504)/(0.01865)= 27 g` Hencemolarmass ofA1 is27 g `mol^(-1)`

Discussion

90108.	A current of 5.0 A is passed through a 100L aqueous solution of sodium soccinate for 4.0h. The gases produced at anode are collected separately at 25^(@)C and 1.0 atm pressure. Find thevolume of gases. Also find the pH of solution at the end of electrylysis . ( Assume that at the start of electrolysis, pH of solution is 7.0 at 25^(@)C)
Answer» Solution :At anode `:`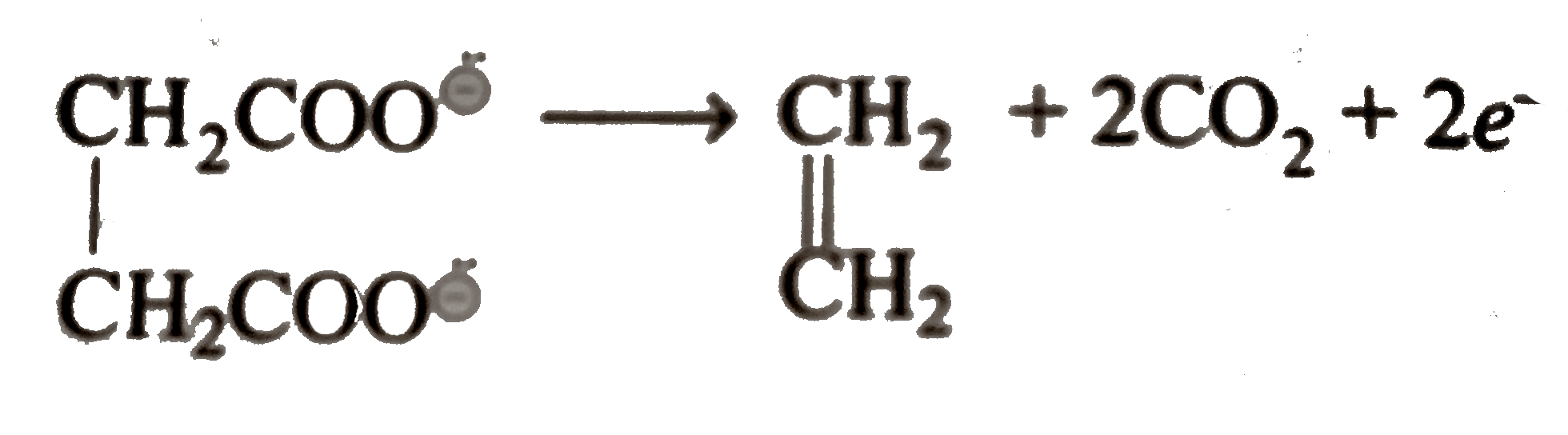 `2F=1mol` of`(CH_(2)=CH_(2)+2mol of CO_(2))` `2F=3 mol `of gases NUMBER of Faradays`=(5xx4xx3600)/(96500)=0.746F` `({:(mol es of gases),(at 25^(@)C and 1 atm):})=(3)/(2)xx0.746~~1.12` `=1.12xx24.48L` `=27.4L` At cathode `:` `2H_(2)O+2e^(-) rarr 2overset(-)(O)H+H_(2)uarr` 2F=2mol `of `OVERSET(-)(O)H` `0.746F=0.746` mol of `overset(-)(O)H` `[overset(-)(O)H]=(0.746Eq)/(100L)=0.007746M` or `N` `:. pOH=2.13` `pH=14-pOH=11.87`

Discussion

90109.	A current of 5 amp is passed through moltenCaCl_(2) for 2 hrs. Calculate the mass of metal as well as mass of non-metal liberated.
Answer» ANSWER :7.5, 13.2 GM

Discussion

90110.	A current of 5 amp is passed through a solution of NaCl for 3.25 hrs . The weight of NaOH formed is
Answer» 6.50 G 17.25g 24.25 g `13.0` g SOLUTION :1gM.mass NaCl`-=`1 g M. mass of NaOH 58.5 NaCl `-=` 40 g NaOH `:.1 F= 96500` Celectricity passed `-= 1g` eq. mass NaOH FORMED `-=40`g of NaOH formed `:.Q=I xxt=5xx3.25xx60xx 60C=Wt. of NaOH` `:. 58500 C =Wt.of NaOH` Wt.of `NaOH=(ixxtxxR)/F=(58500xx 40)/96500=24.25 g`

Discussion

90111.	A current of 40 microampere is passed through a solution of AgNO_(3) for 32 minutes using Pt electrode. A uniform single atom thick of Ag is deposited covering 43% cathode surface. What is the total surface area of cathode if each Ag atom covers 5.4 xx 10^(-16) cm^(2)?
Answer» ANSWER :`602 CM^(2)`

Discussion

90112.	A current of 4 ampere was passed for 1.5 hours through a solution of copper sulphate when 3.2 g of copper was deposited. Calculate the current efficiency.
Answer» SOLUTION :`Cu^(2+) +2E^(-)toCu` 1 mole of Cu(63.5g) requries charge`=2F=2xx96500`coulombs `therefore3.2g` Cu will REQUIRE charge`=(2xx96500)/(63.5)xx3.2`coulombs=9726 coulombs Quantity of ELECTRICITY actually passed`=4xx45xx60C=21600C`. Current efficiency`=(9726)/(21600)xx100=45%`.

Discussion

90113.	A current of 40 microampere is passed through a solution of AgNO_(3) for 32 minute using Pt electrodes. An uniform single atom thick layer of Ag is deposited covering 43% cathode surface. What is the total surface area of cathode if each Ag atom covers 5.4 xx 10^(-16) cm^(2) ?
Answer» ANSWER :`601.65 CM^(2) ;`

Discussion

90114.	A current of 3.7 amper is passed for 6 hre between Pt electrodes in 0.5 litre, 2M solution of Ni(NO_(3))_(2). What will be the molarity of solution at the end of electrolysis?
Answer» Solution :Charge in coulombs = current in amp `xx` time in s `= 3.7 xx 6 xx 60 xx 60` = 79920. `THEREFORE` MOLE (faraday) of electric charge `= (79920)/(96500)` `= 0.8283 F`. Eq. of `Ni(NO_(3))_(2)` deompoased on electrolysis = 0.8283. `therefore` m.e. of `Ni(NO_(3))_(2)` decomposed `= 0.8283 xx 1000 = 828.3` Now, m.e. of `Ni(NO_(3))_(2)` solution before electrolysis = NORMALITY `xx` volume (mL) `= 4 xx 500 = 200` {normality `= 2 xx` molarity `= 2 xx 2 = 4`} m.e. of `Ni(NO_(3))_(2)` after electrolysis = 2000 - 828.3 = 1171.7 `therefore` molarity `Ni(NO_(3))_(2)` solution after electrolysis `= (2.34)/(2) = 1.17 M`.

Discussion

90115.	A current of 3.7 A is passed for 6 hrs. between Ni electrodes in 0.5 L of 2M solution of Ni(NO_3)_2 . What will be the molarity of solution at the end of electrolysis?
Answer» ANSWER :B

Discussion

90116.	A current of 3 amp was passed for 2 hour through a solution of CuSO_4 , 3g of Cu^(2+) ions were deposited as Cu at cathode. Calculate percentage current efficiency of the process
Answer» ANSWER :B::D

Discussion

90117.	A current of 2A was passed for 1.5 hours through a solution of CuSO_(4) when 1.6 g of copper was deposited. Calculate percentage current efficiency.
Answer» Solution :Amountof CURRENT required to deposit 1 mole `Cu(63.5 g) = 2 xx 96500` C Current required to deposit 1.6 g of COPPER = `(2 xx 96500 xx 1.6)/63.5 = 4862.99` Current actually PASSED through `=2 x 1.5 xx 60 = 10800` Current efficiency `=(4862.99)/(10800) xx 100 = 45.03 %`

Discussion

90118.	A current of 2.6 ampere was passed through CuSO_4 solution for 380 sec. The amount of Cu deposited is (at .wt. of Cu (63.5):
Answer» 0.3250g 0.635g 6.35g 3.175g Answer :A

Discussion

90119.	A current of 2.6 ampere was passed through CuSO_(4) solution for 380 sec . The amount of Cu deposited is (atomic mass of Cu 63.5)
Answer» `0.3250 G` `0.635` g `6.35` g `3.175 g` Solution :`W = (E xxi XX t)/(96500) = (63.5 xx 2 .6 xx380)/(2 xx 96500) = 0.325` g

Discussion

90120.	A current of 2.0A passed for 5 hours through a molten metal salt deposits 22.2 g of metal (At wt.=177). The oxidation state of the metal in the metal salt is
Answer» `+1` `+2` `+3` `+4` Solution :`Q=2xx5xx60xx60=36000C` THUS, 36000C deposit METAL=22.2 G `therefore96500C` will deposit metal `=(22.2)/(36000)xx96500g=59.5g` Thus, EQ. wt. of the metal=59.5 Valency or ox. State=At. Wt./Eq. wt. `=177//59.3=3`.

Discussion

90121.	A current of 2 ampere was passed through solutions of CuSO_(4) and AgNO_(3) in series . 0.635 g of copper was deposited . Then the weight of silver depositedwill be
Answer» `0.59` g `3.24` g `1.08` g `2.16` g Solution :A/c. to FARADAY's `II^(ND)` law or `(0.635)/(63.5//2) = (w_(AG))/(108)` `therefore W_(Ag)= 2.16 g `

Discussion

90122.	A current of 2.0 A when passed for 5 hours through a molten metal salt deposits 22.2 g of metal of atomic weight 177. The oxidation state of metal in the metal salt is
Answer» `+1` `+2` `+3` `+4` ANSWER :C

Discussion

90123.	A current of 2 ampere passing for 5 hr through a molten tin salt deposits 22.2 g of tin. Find theoxidation number of tin (atomic weight of tin is 118.7) in the salt
Answer» SOLUTION :`q=it , 2 xx 5 xx 60 xx 60 to 22.2` ` N xx 96,500 larr 118.7` n = oxidation number , n =2

Discussion

90124.	A current of 2 ampere passing for 5 hr through a molten tin salt deposits 22.2 g of t tin. Find the oxidation number of tin in the salt.
Answer» Solution :`Sn^(N+) + n E rarr Sn` For Sn `""(w)/(E) = (i xx t)/(96500)` `(22.2)/(118//n) = (2 xx 5 xx 60 xx 60)/(96500) "" :. n = 2`

Discussion

90125.	A current of 2 amp passing for 5 hours through a molten tin salt deposites 22.2 g of tin. The oxidation state in the tin in the salt is
Answer» `+4` `+3` `+2` `+1` ANSWER :C

Discussion

90126.	A current of 1.70 A is passed through 300.0 ml of 0.160 M solution of ZnSO_(4) for 230 sec with a curent efficiency of 90 percent. Find out the molarity of Zn^(2+) after the deposition of zinc. Assume the volume of the solution to remain constant during electrolysis.
Answer» Solution :QUANTITY of electricity PASSED=`1.70xx230C=391C` As current efficiency=90% `therefore` Effective charge`=(90)/(100)xx319C=351.9C` `Zn^(2+)+2e^(-)TOZN` `2xx96500C` deposit `Zn^(2+)=1` mole `therefore351.9C` will deposit `Zn^(2+)=(1)/(2xx96500)xx351.9`mole=0.0018mole `Zn^(2+)` ions present originally in 300 ml of 0.160 M `ZnSO_(4)=(0.160)/(1000)xx300=0.048` mole `therefore`Amount of `Zn^(2+)` in 300 ml of solution after deposition of `Zn=0.048-0.0018=0.0462`mole `therefore`Molarity of `Zn^(2+)` after deposition of `Zn=(0.0462)/(300)xx1000=0.154M`

Discussion

90127.	A current of 1.70 A is passed through 300 ML of a 0.16 M solution of ZnSO_(4) for 230 s with a current efficienty of 90%. Find out molarity of Zn^(2+) after the deposition of Zn. Assume the volume of the solution to remain constant during the electrolysis.
Answer» Solution :Mole of electric CHARGE `= (1.70 xx 230)/(96500) = 0.004052 F`. `therefore` eq. of Zn to be deposited for 100% CURRENT efficiency = 0.004052 or mole of Zn to be deposited for 100% current efficiency = 0.004052/2 = 0.002026 or mole of Zn to be deposited for 90% current efficiency `= 0.9 xx 0.002026 = 0.00118234` Initial mole of Zn (or `ZnSO_(4)`) `= 0.16 xx 0.3 = 0.48`. Mole of Zn remained undeposited = 0.048 - 0.0018234 `= 0.0461766`. MOLARITY after electrolysis `= (0.0461766)/(0.3) = 0.154 M`

Discussion

90128.	A current of 1.608 A is passed through 250 mL of 0.5 M solution of copper sulphate for 50 minutes. Calculate the strength of Cu^(2+) after electrolysis assuming volume to be constant and the current efficiency is 100%.
Answer» Solution :`"Given,"I= 1.609A""t="50 min(or)"50xx60=3000S""V=250mL` `C=0.5M""eta=100%` The number of Faraday.s of ELECTRICITY passed through the `CuSO_(4)` solution `rArr""Q=It rArr Q=1.608xx3000` `Q=4824C` `therefore"Number of Faraday.s of electricity "=(4824C)/(96500C)=0.5F` Electrolysis of `CuSO_(4)` `Cu_((aq))^(2+)+2e^(-)rarrCu_((s))^(-)`. The above equation shows that 2F electricity will DEPOSIT 1 mole of `CU^(2+)` `therefore0.5F" electricity will deposit"(1mol)/(2F)xx0.5F="0.025 mol"` `"Initial number of molar of "Cu^(2+)" in 250 ml of solution"=(0.5)/(1000)xx250mL=0.125mol` `therefore"Number of molar "Cu^(2+)" after electrolysis "=0.125-0.025=0.1mol` `therefore"Concentration of "Cu^(2+)=("0.1 mol")/("250 mL")xx"1000 mL"=0.4M`

Discussion

90129.	A current of 1.608A is passed through 250 mL of 0.5 M solution of copper sulphate for 50 minutes. Calculate the strength of Cu^(2+) after electrolysis assuming volume to be constant and the current efficiency is 100%.
Answer» Solution :Given : I = 1.608A, t = 50 MIN = `50 times 60` V = 500 mL C = 0.5 M `" "`= 3000 S `eta=100%` Calculate the number of FARADAYS of electricity passed through the `CuSO_(4)` solution `rArr Q=It` `" "Q=1.608 times 3000` `" "Q=4824C` `therefore` number of Faradays of electricity `=(4824C)/(96500C)` `""=0.5F` Electrolysis of `CuSO_(4)` `Cu_((aq))^(2+)+2e^(-) rarr Cu_((s))` The above equation shows that 2F electricity will deposit 1 mole of `Cu^(2+)` to. `therefore` 0.5F electricity will deposit `(1mol)/(2F) times 0.5F=0.025 mol` Initial number of molar of `Cu^(2+)` in 250 ml of solution `=0.5/(1000mL) times 250mL` `""=0.125mol` `therefore` number of `Cu^(2+)` after electrolysis `""=0.125-0.025` `""=0.1` mol `therefore` CONCENTRATION of `Cu^(2+)=(0.1mol)/(250mL) times 1000mL` `""=0.4` M.

Discussion

90130.	A current of 1.50 A was passed through an electrolytic cell containing AgNO_(3) solution with inert electrodes. The mass of the silver deposited at cathode was 1.50 g. How long did the current flow? (Atomic mass of Ag=108u, F=96500C).
Answer» ANSWER :893.5 s

Discussion

90131.	A current of 12 ampere is passed through an electrolytic cell containing aqueous NiSO_(4) solution. Both Ni and H_2 gas are formed at the cathode. The current efficiency is 60% . What is the mass of nickel deposited on the cathode per hour ?
Answer» 7.883 g 3.941 g 5.91 g 2.645 g Solution :At cathode`:Ni^(2+) + 2e^(-) rarr Ni` Now, equivalent weight of `Ni = ("MOLECULAR weight")/("electron GAIN")` `= (58.7)/(2) =29.35` GIVEN i = 12 A, t=1 hr `=60 xx 60 sec` `Z = ("equivalent weight")/("96500")` Weight of deposited Ni `= ("ZIT" xx "efficiency")/(100)` `= (29.35 xx 12 xx 60 xx60)/(96500 xx 100) xx 60 = 7.883 g`

Discussion

90132.	A current of 1.5 A is passed through 500 mL of 0.25 M solution of zinc sulphate for 1 hr with a current efficiency of 90% . Calculate the final molarity of Zn^(2+) assuming volume to be constant .
Answer» Solution :Quantity of ELECTRICITY passed , `Q = I xx t` `I = 1.5 xx (90)/(100) , t = 1 xx 60 xx 60 = 3600` s ` Q = 1.5 xx (90)/(100) xx 3600` `= 4860 C` Faraday of electricity passed = `(4860)/(96500) = 0.05F` Now `Zn^(2+) + 2 e^(-) to Zn` 2 F of electricity convert 1 mol of `Zn^(2+)` to Zn . 0.05 F of electricity will convert `Zn^(2+)` to Zn = `1/2 xx 0.05` `= 0.025` mol Initial moles of `Zn^(2+)` in 500 mL solution = `(0.25)/(1000) xx 500` `= 0.125` mol Moles of `Zn^(2+)` ions left in the solution = `0.125 - 0.025` = 0.10mol `therefore` Final molarity of `Zn^(2+)` solution = `(0.1)(500) xx 1000` `= 0.2 ` M

Discussion

90133.	A current of 1.50 A was passed through an electrolytic cell containing AgNO_3 solution with inert electrodes. The weight of silver deposited was 1.50 g. How long did the current flow ? [Molar mass of Ag = 108 g mol^(-1)?, 1 F = 96500 C mol^(-1)]
Answer» Solution :Quantity of charge REQUIRED to DEPOSIT 108 g Ag = 96500 C Quantity of charge required to deposit 1.5 g Ag `=(96500)/108 xx 1.5 = 1340.28 C` TIME taken `=Q/l = (1340.28)/1.50 = 893.5s`

Discussion

90134.	A current of 1.5 amperes is passed through a solution of a salt of a bivalent metal for 30 minutes. Increase in mass of cathode is 0.8898 g. Find the atomic mass of the metal.
Answer» ANSWER :63.6

Discussion

90135.	A current of 12 ampere is passed through an electrolytic cell containing aq. NiSO_(4) solution . Both Ni and H_(2) gas are formed at the cathode . The current efficiency is 60% . What is the mass of nickel deposited on the cathode per hour ? (At.mass of Ni = 98.7)
Answer» 5.91 G 3.941 g 7.883 g 2.645 g Solution :`Q= I xx t (s) 12 xx 60 xx 60 = 43200` C . `Ni^(2+) + 2e^(-) to Ni` . Theortically, `2 xx 96500` C will deposit Ni = 58.7 g . Hence , 43200 C will deposit Ni = 13.137 g . As current efficiency is 60 % , MASS actually deposited = `(60)/(100) xx 13.137` = 7.88 g .

Discussion

90136.	A current of 10.0A is passed through 1.0L of 1.0M HCl solution for 965 seconds, pH of the solution at the end of the experiment is:-
Answer» 0 0.2 0.8 none of the above Solution :1L of 1.0 M HCl solution contains 1 mole of HCl. `H^(+)+e^(-)to(1)/(2)H_(2)` 1 FARADAY PRODUCES 0.5 mole of `H_(2)` `(965xx10)/(96500)` faraday produces`=(0.5xx965xx10)/(96500)` `=0.05` mole of `H_(2)` `0.05` mole of `H_2` contains 0.1 mole H. `therefore0.9` mole `H^+` left in solution. `pH=-log[0.9]=0.125`.

Discussion

90137.	A current of 10 amp is passed through molten AlCl_(3) for 96.5 seconds. Calculate the mass of Al deposited.
Answer» ANSWER :0.09 G

Discussion

90138.	A current of 10 amp is passed through molten AlCl_(3)for 96.5 seconds. Calculate the mass of Al deposited at the cathode (At. wt of Al = 27 )
Answer» ANSWER :0.09 GM

Discussion

90139.	A current of 1.0 A was passed for 2 hr through a solution of cuprocyanide and 0.3745 g of copper was deposited on the cathode. Calculate the current efficiency for the copper deposition. (Cu-63.5)
Answer» `79%` `39.5%` `63.25%` `63.5%` SOLUTION :m(THEORETICAL)`=(63.5xx0.1xx7200)/(96500)=0.4738g` `THEREFORE%` EFFICIENCY `=(0.3745)/(0.4738)xx100=79%`

Discussion

90140.	A current of 10 A is applied for 1 h to 1 litre of a solution containing 1 mole of HCl. Calculate the pH of the solution at the end of this time.
Answer» SOLUTION :At the cathode, `H_(2)` is discharged. At the anode `Cl_(2)` is preferentially discharged over `O_(2)`. Thus during ELECTROLYSIS, Hcl is lost from the solution. Eq. of HCl lost = NUMBER of faradays used `= (10 XX 60 xx 60)/(96500) = 0.373` or, mole of HCl lost = 0.373. Mole of Hcl remained/litre = 1.0 - 0.373 = 0.627. `therefore` pH = -log(0.627) = 0.20.

Discussion

90141.	A current of 1 ampere is paased for one hour between nickel electrodes in 0.5 L of 2 M Ni (NO_(3))_(2) solution. What will be the molarity of the solution at the end of the electrolysis?
Answer» SOLUTION :The CHANGES taking PLACE at the electrodes in the ELECTROLYSIS of `Ni(NO_(3))_(2)` solution using nickel electrodes will be as follows: At cathode: `Ni^(2+)+2etoNi` At anode: `NitoNi^(2+)+2e^(-)` thus, amount of nickel deposited on the cathode from the solution=nickel dissolved from the anode. Hence, molarity of the solution will REMAIN unchanged at the end of the electrolysis.

Discussion

90142.	A current of 0.96 A is passed for 3 hours between Ni electrodes in 0.5 L of 92 M solution Ni(NO_(3))_(2) . The molarity of the solution after electrolysis is would be -
Answer» `0.92` M `0.625` M `0.22` M `1.25` M SOLUTION :`Q = I xx t = 9.65 xx 3 xx 60 = 104220 ` C . `Ni^(2+)+ 2e^(-) to Ni` `2 xx 96500 C ` deposit 1 MOLE of `Ni^(2+)` , `THEREFORE 104220 C` will deposit `Ni^(2+)` `= (1)/(2 xx 96500) xx 104220 = 0.54` mole ORIGINALLY 0.5 L of 2 M solution contain `Ni^(2+) = 1` mole . Now 0.5 L will contain `Ni^(2+) = 1 - 0.54 = 0.46` mole . Hence molarity = `(n)/(V(L)) = (0.46)/(0.5) = 0.92 MOL L^(-1)`.

Discussion

90143.	A currentof 0.965 amp. Is passed through an aqueous solutionof AgNO_(3) for 10 minutes during electroysis, Calculate the mass of Ag deposited at the cathode (Atomic weight of Ag=108).
Answer» ANSWER :0.648 GM

Discussion

90144.	A current of 0.5 amperes is passed for 30 minute through a voltmeter containing CUSO_4 Solution. Find the weight of Cu deposited
Answer» 3.18 g 0.318 g 0.296 g 0.150 g Solution :`W=ZxxIxxt` `Z=(E)/(96500)=(Mol.wt.//2)/(96500)`[for copper, E=mol. Wt/2] Given, CURRENT passed=0.5A time=30mins=`30xx60s` `W=(63.5)/(2)xx(1)/(96500)xx0.5xx30xx60=0.296g`.

Discussion

90145.	A current of 0.5 ampere when passed through AgNO_(3)solution for 193 seconds deposited 0.108 g. of silver. The equivalent weight of Ag is
Answer» 10.8 108 54 1 Answer :B

Discussion

90146.	A current of 0.5 A is passed through acidulated water for 30 minute. Calculate weight of H_(2) and O_(2) evolved. Also calculate the volume of O_(2) produced at 25^(@)C and 760 mm of Hg, if the gas is : (a) dry (b) saturated with water vapour (aqueous tension is 23.0 mm at 25^(@)C).
Answer» Answer :`H_(2) = 9.33 XX 10^(-3)G`, `O_(2) = 7.46 xx 10^(-2)g`, (a) `5.7 xx 10^(-2)` litre, (B) `5.88 xx 10^(-2)` litre;

Discussion

90147.	A current of 0.5 ampere when passed through AgNO_(3) solution for 193 seconds deposited 0.108 g of Ag. The equivalent weight of Ag is
Answer» 10.8 108 54 1 Answer :B

Discussion

90148.	A current of 0.5 amp is sent through a solution of CuSO_(4) for 20 minutes using Pt electrodes. (a) Calculate the weight of Cu deposited. (b) Find out the total number of copper atoms deposited. (Cu = 6.57, Av. constant = 6.022 xx 10^(23), 1 F = 96500 coulombs)
Answer» SOLUTION :`0.1976 G, 1.87 XX 10^(21)`

Discussion

90149.	A current of0.4 ampere is passed for 30 minutes through a voltameter containing CuSO_(4) solution. The weight of Cu dpeosited will be
Answer» 3.18g 0.318g 0.296g 0.150g Solution :`Q=1xxt=0.5xx30xx60=900C` `CU^(2+)+2E^(-)rarrCu` `2xx96500C` DEPOSIT `Cu=63.5g` `THEREFORE 900C` will deposit Cu `=(63.5)/(2xx96500)xx900=0.296g`

Discussion

90150.	A current of 0.2ampere is passes through a solution of CuSO_4 for 10 minutes calculate the man of Cu deposited on the cathode.
Answer» Solution :`W=Q L t` `W=E/96500 TIMES I t` `=(31.75 times 0.2 times 10 times 60)/96500` `=0.03948 G`

Discussion

Explore topic-wise InterviewSolutions in .

A current of 9.65 ampere folwing for 10 minute depostits 3.0 g of a metal. The equivalent weight of the metal is :

A current of 9.65ampere flowing for 10 minutes deposits 3.0g of the metal which is monovalent. The atomic mass of the metal is:

A Current of 9.65 ampere flowing for 10 minutes deposits 3.0g of themetal which is monovalent. The atomci mass of the metal is

A current of 9.65 A is passed for 3 hours between nickel electrodes in 0.5 L of a 2 M solution of Ni(NO_3)_2. The molarity of the solution after electrolysis would be

A current of 9.65 A is passed for 3 hours between platinum electrodes immersed in 0.5 dm^(3) solutionof concentration 2 mol dm^(-3) Ni(NO_3)_2. The molarity of solution after electrolysis would be

A current of 96.5 A is passed for 18 min between nickel electrodes in 500 ml solution of 2 M Ni(NO_3)_2. The molarity of solution after electrolysis would be

A currentof 6 amperesis passedthroughA1C1_(3) solutionfor 15 minutesusingPtelectrodes , when0.50 g A1 isproduced.Whatis the molarmass of A1 ?

A current of 5 amp is passed through moltenCaCl_(2) for 2 hrs. Calculate the mass of metal as well as mass of non-metal liberated.

A current of 5 amp is passed through a solution of NaCl for 3.25 hrs . The weight of NaOH formed is

A current of 40 microampere is passed through a solution of AgNO_(3) for 32 minutes using Pt electrode. A uniform single atom thick of Ag is deposited covering 43% cathode surface. What is the total surface area of cathode if each Ag atom covers 5.4 xx 10^(-16) cm^(2)?

A current of 4 ampere was passed for 1.5 hours through a solution of copper sulphate when 3.2 g of copper was deposited. Calculate the current efficiency.

A current of 40 microampere is passed through a solution of AgNO_(3) for 32 minute using Pt electrodes. An uniform single atom thick layer of Ag is deposited covering 43% cathode surface. What is the total surface area of cathode if each Ag atom covers 5.4 xx 10^(-16) cm^(2) ?

A current of 3.7 amper is passed for 6 hre between Pt electrodes in 0.5 litre, 2M solution of Ni(NO_(3))_(2). What will be the molarity of solution at the end of electrolysis?

A current of 3.7 A is passed for 6 hrs. between Ni electrodes in 0.5 L of 2M solution of Ni(NO_3)_2 . What will be the molarity of solution at the end of electrolysis?

A current of 3 amp was passed for 2 hour through a solution of CuSO_4 , 3g of Cu^(2+) ions were deposited as Cu at cathode. Calculate percentage current efficiency of the process

A current of 2A was passed for 1.5 hours through a solution of CuSO_(4) when 1.6 g of copper was deposited. Calculate percentage current efficiency.

A current of 2.6 ampere was passed through CuSO_4 solution for 380 sec. The amount of Cu deposited is (at .wt. of Cu (63.5):

A current of 2.6 ampere was passed through CuSO_(4) solution for 380 sec . The amount of Cu deposited is (atomic mass of Cu 63.5)

A current of 2.0A passed for 5 hours through a molten metal salt deposits 22.2 g of metal (At wt.=177). The oxidation state of the metal in the metal salt is

A current of 2 ampere was passed through solutions of CuSO_(4) and AgNO_(3) in series . 0.635 g of copper was deposited . Then the weight of silver depositedwill be

A current of 2.0 A when passed for 5 hours through a molten metal salt deposits 22.2 g of metal of atomic weight 177. The oxidation state of metal in the metal salt is

A current of 2 ampere passing for 5 hr through a molten tin salt deposits 22.2 g of tin. Find theoxidation number of tin (atomic weight of tin is 118.7) in the salt

A current of 2 ampere passing for 5 hr through a molten tin salt deposits 22.2 g of t tin. Find the oxidation number of tin in the salt.

A current of 2 amp passing for 5 hours through a molten tin salt deposites 22.2 g of tin. The oxidation state in the tin in the salt is

A current of 1.70 A is passed through 300.0 ml of 0.160 M solution of ZnSO_(4) for 230 sec with a curent efficiency of 90 percent. Find out the molarity of Zn^(2+) after the deposition of zinc. Assume the volume of the solution to remain constant during electrolysis.

A current of 1.70 A is passed through 300 ML of a 0.16 M solution of ZnSO_(4) for 230 s with a current efficienty of 90%. Find out molarity of Zn^(2+) after the deposition of Zn. Assume the volume of the solution to remain constant during the electrolysis.

A current of 1.608 A is passed through 250 mL of 0.5 M solution of copper sulphate for 50 minutes. Calculate the strength of Cu^(2+) after electrolysis assuming volume to be constant and the current efficiency is 100%.

A current of 1.608A is passed through 250 mL of 0.5 M solution of copper sulphate for 50 minutes. Calculate the strength of Cu^(2+) after electrolysis assuming volume to be constant and the current efficiency is 100%.

A current of 1.50 A was passed through an electrolytic cell containing AgNO_(3) solution with inert electrodes. The mass of the silver deposited at cathode was 1.50 g. How long did the current flow? (Atomic mass of Ag=108u, F=96500C).

A current of 12 ampere is passed through an electrolytic cell containing aqueous NiSO_(4) solution. Both Ni and H_2 gas are formed at the cathode. The current efficiency is 60% . What is the mass of nickel deposited on the cathode per hour ?

A current of 1.5 A is passed through 500 mL of 0.25 M solution of zinc sulphate for 1 hr with a current efficiency of 90% . Calculate the final molarity of Zn^(2+) assuming volume to be constant .

A current of 1.50 A was passed through an electrolytic cell containing AgNO_3 solution with inert electrodes. The weight of silver deposited was 1.50 g. How long did the current flow ? [Molar mass of Ag = 108 g mol^(-1)?, 1 F = 96500 C mol^(-1)]

A current of 1.5 amperes is passed through a solution of a salt of a bivalent metal for 30 minutes. Increase in mass of cathode is 0.8898 g. Find the atomic mass of the metal.

A current of 12 ampere is passed through an electrolytic cell containing aq. NiSO_(4) solution . Both Ni and H_(2) gas are formed at the cathode . The current efficiency is 60% . What is the mass of nickel deposited on the cathode per hour ? (At.mass of Ni = 98.7)

A current of 10.0A is passed through 1.0L of 1.0M HCl solution for 965 seconds, pH of the solution at the end of the experiment is:-

A current of 10 amp is passed through molten AlCl_(3) for 96.5 seconds. Calculate the mass of Al deposited.

A current of 10 amp is passed through molten AlCl_(3)for 96.5 seconds. Calculate the mass of Al deposited at the cathode (At. wt of Al = 27 )

A current of 1.0 A was passed for 2 hr through a solution of cuprocyanide and 0.3745 g of copper was deposited on the cathode. Calculate the current efficiency for the copper deposition. (Cu-63.5)

A current of 10 A is applied for 1 h to 1 litre of a solution containing 1 mole of HCl. Calculate the pH of the solution at the end of this time.

A current of 1 ampere is paased for one hour between nickel electrodes in 0.5 L of 2 M Ni (NO_(3))_(2) solution. What will be the molarity of the solution at the end of the electrolysis?

A current of 0.96 A is passed for 3 hours between Ni electrodes in 0.5 L of 92 M solution Ni(NO_(3))_(2) . The molarity of the solution after electrolysis is would be -

A currentof 0.965 amp. Is passed through an aqueous solutionof AgNO_(3) for 10 minutes during electroysis, Calculate the mass of Ag deposited at the cathode (Atomic weight of Ag=108).

A current of 0.5 amperes is passed for 30 minute through a voltmeter containing CUSO_4 Solution. Find the weight of Cu deposited

A current of 0.5 ampere when passed through AgNO_(3)solution for 193 seconds deposited 0.108 g. of silver. The equivalent weight of Ag is

A current of 0.5 A is passed through acidulated water for 30 minute. Calculate weight of H_(2) and O_(2) evolved. Also calculate the volume of O_(2) produced at 25^(@)C and 760 mm of Hg, if the gas is : (a) dry (b) saturated with water vapour (aqueous tension is 23.0 mm at 25^(@)C).

A current of 0.5 ampere when passed through AgNO_(3) solution for 193 seconds deposited 0.108 g of Ag. The equivalent weight of Ag is

A current of 0.5 amp is sent through a solution of CuSO_(4) for 20 minutes using Pt electrodes. (a) Calculate the weight of Cu deposited. (b) Find out the total number of copper atoms deposited. (Cu = 6.57, Av. constant = 6.022 xx 10^(23), 1 F = 96500 coulombs)

A current of0.4 ampere is passed for 30 minutes through a voltameter containing CuSO_(4) solution. The weight of Cu dpeosited will be

A current of 0.2ampere is passes through a solution of CuSO_4 for 10 minutes calculate the man of Cu deposited on the cathode.