InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 9601. |
Draw the graph of f(x)=[cot^(-1)x]," where "[*] representsthe greatest integer funtion. |
|
Answer» Solution :Given `F(X)=[cos^(-1)x]` `cot^(-1)x`is a decreasing function in R. So `[cot^(-1)x]` is discontinuous whn `cot^(-1)x` is an interger. Now `0lecot^(-1)x lepi" for "x in R` So `[cot^(-1)x]` is discontinuous when`cot^(-1)x=1,2,3` or`x=cot1, cot2, cot3` When `[cot^(-1)x]=0,0lecot^(-1)xlt1:.cot1ltxleoo` When `[cot^(-1)x]=1,1lecot^(-1)xlt2:.cot2ltxlecot1` ltbrtgt When `[cot^(-1)x]=2,2lecot^(-1)xlt3:.cot3ltxlecot2` `[cot^(-1)x]=3,3lecot^(-1)xltpi:.-ooltxlecot3` So the graph of `f(x)[cot^(-1)x]` can be DRAWN as FOLLOWS. 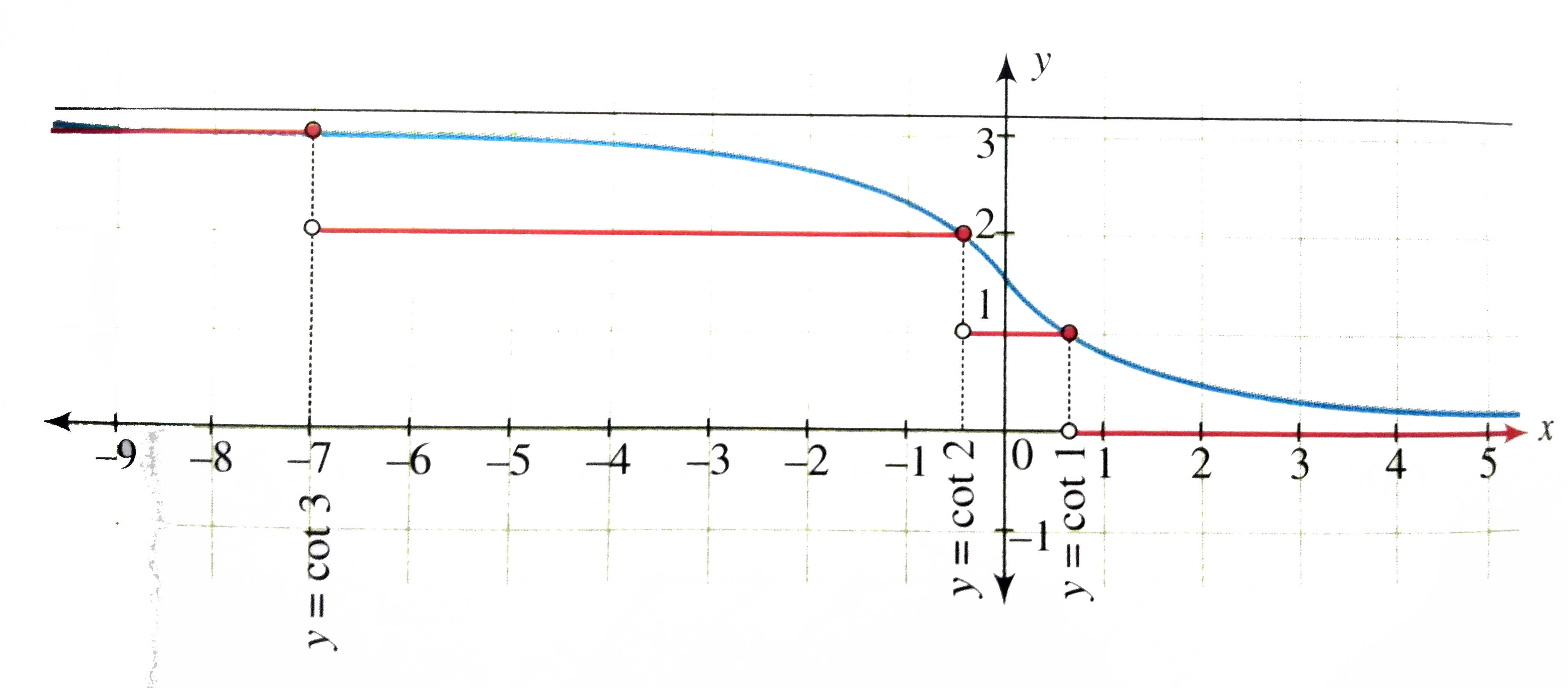
|
|
| 9602. |
int (x^(2))/((a+bx)^(2))dx=? |
|
Answer» `(-x^(2))/(B(a+bx))+(2)/(b^(2)) [x-(a)/(b) log (a+bx)]+C` |
|
| 9603. |
The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is |
|
Answer» 0.4 |
|
| 9604. |
If ABCDE is a regular penatagon then : bar(AB)+bar(BC)+bar(AD)+bar(ED)+bar(AE)= |
|
Answer» `BAR(AC)-2bar(DC)` |
|
| 9605. |
Show that the points (a+5,a-4),(a-2,a+3) and (a,a) do not lie on a straight line for any value of a |
|
Answer» |
|
| 9607. |
Five distinct 2-digit numbes are in a geometric progression. Find the middle term. |
|
Answer» |
|
| 9608. |
Evaluate the following integrals. int(1)/((x+2)sqrt(x))dx |
|
Answer» |
|
| 9609. |
Let log_(c)ab = x, log_(a)bc = y and log_(b) ca = z. Find the value of (xyz - x - y - z). |
|
Answer» <P> |
|
| 9610. |
Let f be a fuction definated on (-1, 1) by f(x)=(cos ^-1 (1-{x}^2)sin^-1(1-{x}))/({x}-{x})^3 ,x ne 0 and {.} is the fractional part function. Which of the following statements is correct ? |
|
Answer» `lim_(xto 0^+) f(x)` EXISTS and equals `(pi)/(sqrt(2))` |
|
| 9611. |
Which of the following represent(s) DeltaH_("atomization",H_(2)O(s))^(@) ? |
|
Answer» `DeltaH_("sublimation",H_(2)O(s))^(@)+2DeltaH_(BE,O-H)^(@)` (A) `DeltaH_("atomization",H_(2)O(s))^(@)=DeltaH_("sublimation",H_(2)O(s))^(@)+2DeltaH_(BE,O-H)^(@)` ( C) `DeltaH_("atomization",H_(2)O(s))^(@)=-DeltaH_("formation",H_(2)O(s))^(@)+Delta_(BE,H-H)^(@)+(DeltaH_(BE,O=O)^(@))/(2)` ( D) `DeltaH_("atomization",H_(2)O(s))^(@)=DeltaH_("fusion",H_(2)O(s))^(@)+DeltaH_("atomisation"H_(2)O(l))^(@)` |
|
| 9612. |
If the position vectors of vertices of triangle ABC are 3hat(i)+hat(j)+2hat(k),hat(i)-2hat(j)+7hat(k)and-2hat(i)+3hat(j)+5hat(k), then the triangle ABC is |
|
Answer» RIGHT ANGLED and isosceles |
|
| 9613. |
If P and Q are symmetric matrices of the same order then PQ-QP is |
|
Answer» ZERO matrix |
|
| 9614. |
If |z_(1)+ z_(2)|=|z_(1)|+|z_(2)|, then arg z_(1) - arg z_(2) is |
|
Answer» `0` |
|
| 9615. |
(i) Let -1 le p le 1. Show that the equation 4x^(3) - 3x - p = 0 has a unique root in the interval [1/2, 1] and identiify it. (ii) Let f(x), x ge 0, be a nonnegative continuous function , and letF'(x) = f(x)= (4a-3)(x+log5)+2(a-7)cotx/2 sin^(2) x/2, x ge 0. If for some c gt 0, f(x) ltcF(x)for all x ge 0, then show that f(x) = 0for all x ge 0, then show that f(x) = 0 for all x ge 0. |
| Answer» | |
| 9616. |
By using Gaussian elimination method, balance the chemical - reaction equation : C_(2)H_(6)+O_(2)to H_(2)O+CO_(2) |
|
Answer» |
|
| 9617. |
A monopolist's demand function is x = 50 - (P)/4At what price is marginal revenue zero? |
|
Answer» |
|
| 9619. |
A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2)) =1. If this tangent is intersected by the tangents at the vertices at points P and Q, then which of the following is/are true |
|
Answer» S,S',P and Q are concyclic 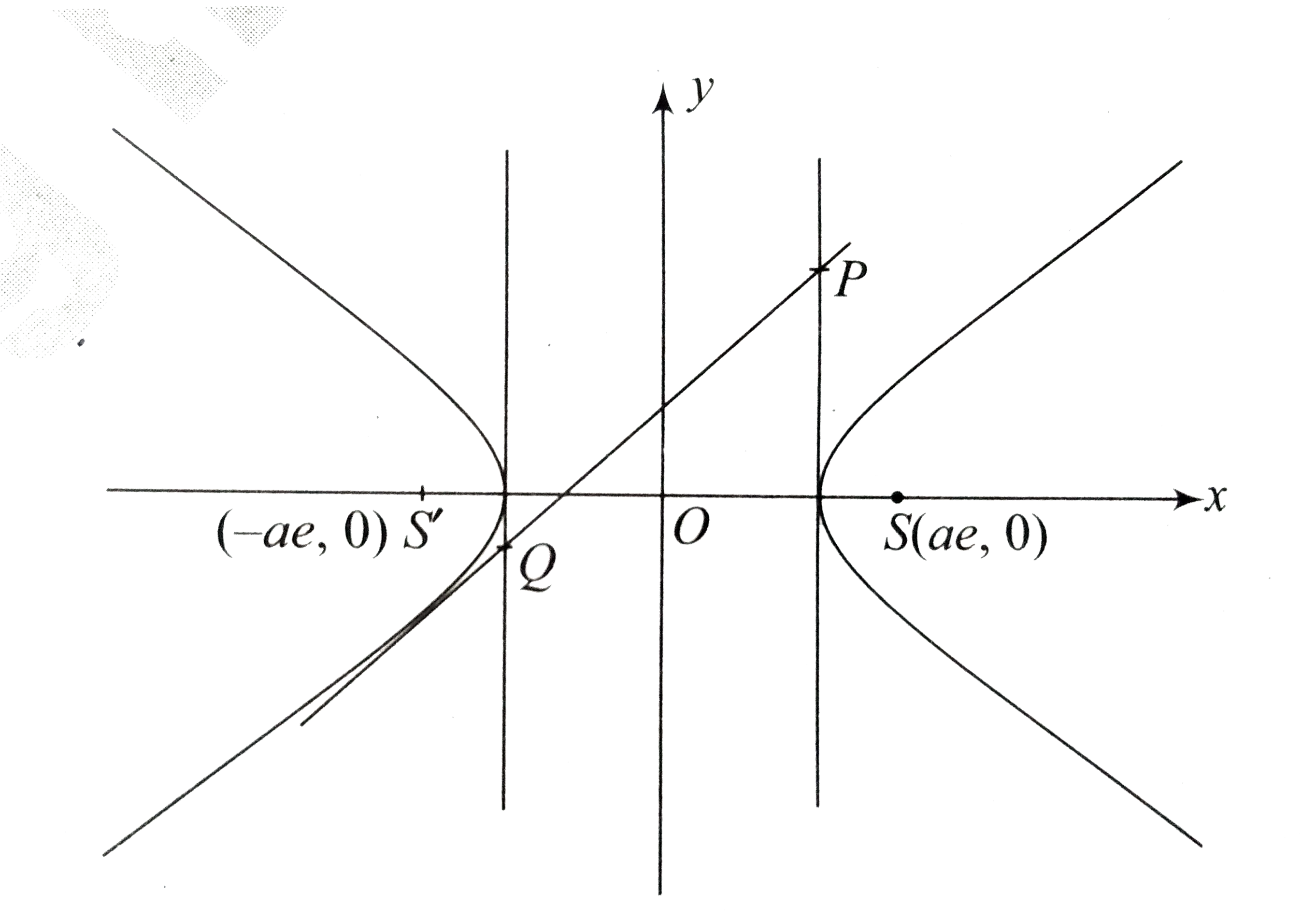 Any tangent to the hyperbola is `(X sec THETA)/(a) -(y TAN theta)/(b) =1` Solving this line with the lines `x = +-a`, we get the COORDINATES of points P and Q as `(a,b tan.(theta)/(2))` and `(-a,-b cot.(theta)/(2))` Now slopes of the lines PS and QS are `m_(PS) =(btan.(theta)/(2))/(a(1-e)), m_(QS) =(-b cot.(theta)/(2))/(-a(1+e))` `rArr m_(PS).m_(QS) =(-b^(2))/(a^(2)(e^(2)-1)) =-1` Similarly `m_(PS). m_(QS') =-1` `rArr` line PQ subtends and angle of `(pi)/(2)` at S and S' `rArr` points P,Q,S and S' are concyclic. `rArr PQ` is diameter. |
|
| 9620. |
f : R^(+) to R^(+): f(x)= e^(x)is |
|
Answer» many - oneand into For each `x in R^(+) EE" log" x in R^(+) s.t f(log x )=x` `So , FIN onto. |
|
| 9621. |
If the number of terms in the expansion of (1+5x+10x^(2)+10x^(3)+5x^(4)+x^(5))^(20) is m, then unit's place of 2^(m) is |
|
Answer» 2 |
|
| 9622. |
int (log x)^(4)dx= |
|
Answer» `X[(logx)^(4)-4(logx)^(3)+12(log x)^(2)-24 log x-24]+c` |
|
| 9623. |
Which point lies on the origin side of the plane 2x + 3y + 4z + 7 = 0 ? |
|
Answer» (1, 2, – 7) |
|
| 9624. |
A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l_(1), and that below the piston is l_(2), such that l_(1)gtl_(2). Each part of the cylinder contains n moles of an ideal gas at equal temeprature T. If the pistion is stationary, its mass, m, will be given by : (R is universal gas constant and g is the acceleration due to gravitey) |
|
Answer» `(RT)/(NG)[(l_(1)-3l_(2))/(l_(1)l_(2))]` |
|
| 9625. |
vec(a)=lambda hati+3hatj+2hatk,vec(b)=hati-hatj+3hatk. If vec(a) and vec(b) are perpendicular to each other then find the value of lambda. |
|
Answer» |
|
| 9626. |
Let A={1,2,3,4,5}, B={1,2,3,4) and f:A rarr B is a function, the |
|
Answer» number of onto functions, if N(f(A))=4 is 240 |
|
| 9627. |
Circles are inscribed in the acute angle alpha so that every neighbouring circles touch each other. If the radius of the first circle is R then find the sum of the radii of the first n circles in terms of R and alpha. |
| Answer» SOLUTION :`(R(1-sin.(ALPHA)/(2)))/(2SIN.(alpha)/(2))[((1+sin.(alpha)/(2))/(1-sin.(alpha)/(2)))^n-1]` | |
| 9628. |
Find the centre and radius of the following circles : 4x^2 + 4y^2 - 4x + 12y - 15 = 0 |
|
Answer» Solution :`4X^2 + 4y^2 - 4x + 12y - 15 = 0` or, `x^2 + y^2 -x + 3y - (15)/4 = 0` `therefore` 2g = -1, 2F = 3, c = -15/4 `therefore` G = -1/2, f = 3/2 `therefore` Centre at (-g, -f) = (1/2, -3/2) and radius `sqrt(g^2 + f^2 -c)` = `sqrt(1/4 + 9/4 + (15)/4)` = 5/2 |
|
| 9629. |
If the equation 2x^(2) + 7xy+3y^(2) - 9x - 7y+k=0 represents a pair of lines, then kis equal to |
|
Answer» 4 |
|
| 9630. |
Write the value of underset(-1)overset1int(sin^5x+x)dx. |
| Answer» SOLUTION :`UNDERSET(-1)overset1int(sin^5x+x)dx=0(becausesin^5x+x` is an ODD FUNCTION) | |
| 9631. |
A survey shows that in a city 60% familes own a car, 80% families have a scooter, and 40% have a bicycle. Also 30% own both a Car and scooter, 35% Car and bicycle and 25% scooter and bicycle, and some families owns all the three. Now the families who have neither of the three can be |
|
Answer» 0.07 B = families own a Scooter C = families own a BICYCLE We have to find `rArr n(A. cap B. cap C.) = n(U) - n(A cup B cup C) = 100-[Sigma n(A) - Sigma n(A cap B)+n(A cap B cap C)]` `=100 - [(60 + 80 + 40) - 90 + x]` `= 100 - [90 +x]` `10 - x` [Here `x = n(A cap B cap C) gt 0` and `0 lt x le 10`] So, possible ANSWERS is 7% |
|
| 9632. |
Find the equation of the circle which touches x^(2) + y^(2)-4x + 6y -1 =0at (-1,1)internally with a radius of 2. |
|
Answer» |
|
| 9634. |
For all a,b in N we define a*b =a^(3)+b^(3) Show that * is commutative but not associative |
|
Answer» SOLUTION :(i) For all a,b in N we have ` A*b=a^(3)+b^(3)=b^(3)+a^(3)=b*a` `therefore` * is comutative (ii) `(1*2)*3=(1^(3)+2^(3))*3=(9*3)=(3^(3)+3^(3))` =729+27=756 `1*(2*3)=1&*(2^(3)+3^(3))=1*(8+274)=1*35` `=1^(3)+(35)^(3)` `therefore (1*2)*3 NE 1*(2*3)` |
|
| 9635. |
If the domain of f(x)=-|x|+2 " is " -1lexle3 f(x) has a minimum value when x equals |
|
Answer» -1 An alternative solution is to realize that y is SMALLEST when x is largest because of the negative absolute value [11] |
|
| 9637. |
By Simpson's formula, approximate the integral I =int_(1.05)^(1.36) f(x)dx If the integrand is defined by the followingtable : {:(x,1.05,1.10,1.15,1.20,1.25,1.30,1.35),(f(x),2.36,2.50,2.74,3.04,3.46,3.98,4.6):} |
|
Answer» |
|
| 9638. |
Express 1+isqrt2=r cos theta +sin thetacomplex numbers in the polar form. |
|
Answer» Solution :where `R =sqrta^2+b^2=sqrt(1^2+2)=sqrt3` `"and"THETA=TAN^(-1)(sqrt2/1)=tan^(-1)sqrt2` `:. 1 +isqrt2=sqrt3(costheta+isin theta),"where tan theta=sqrt2` |
|
| 9639. |
If each root of the equation 2x^(3)+ax^(2)-8x+b=0 is reduced by one, then in the transformed equation thus formed, the term containing x^(2) and the constant term are vanishing. The roots of the original equation are |
|
Answer» 1,-3,2 |
|
| 9640. |
If C_(r) = .^(n)C_(r) then prove that (C_(0) + C_(1)) (C_(1) + C_(2)) "….." (C_(n-1) + C_(n)) = (C_(1)C_(2)"…."C_(n-1)C_(n))(n+1)^(n)//n! |
|
Answer» Solution :We have, `(C_(0)+C_(1))(C_(1)+C_(2))(C_(2)+C_(3))"...."(C_(N-1)+C_(n))` `=C_(1)C_(2)"...."C_(n-1)C_(n)(1+(C_(0))/(C_(1)))(1+(C_(1))/(C_(2)))(1+(C_(2))/(C_(3)))"....."(1+(C_(n-1))/(C_(n)))` `=C_(1)C_(2)"...."C_(n-1)C_(n)(1+1/n)(1+2/(n-1))(1+3/(n-2))"...."(1+n/1)` `=C_(1)C_(2)"....."C_(n-1)C_(n)((n+1)^(n))/(n!)` |
|
| 9641. |
I : For any vector a, (a xx i)^(2) + (a xx j)^(2) + (a xx k)^(2) = 2a^(2) and (a. i)^(2) + (a.j)^(2) + (a.k)^(2) = a^(2) II : If (2i + 4j + 2k) xx (2i - xj + 5k) = 16 I - 6j + 2xk then x = 2 |
|
Answer» only I is ture |
|
| 9642. |
A tankcontains 1000 litres of water in which 100 grams of salt is dissolved Salt solution runs at a rate 10 litres per minute , each litre contains 5 grams of dissolved salt . The mixtureof the tank is keptuniform by stirring . Salt solution runs out at 20 litres per minute . Find the amount of salt at any time . |
|
Answer» |
|
| 9643. |
Find lambda so that the scalar projection of veca=lambdahati+hatj+4hatk onvecb=2hati+6hatj+3hatk is 4units |
|
Answer» 5 |
|
| 9644. |
If x + iy = (1)/((1 + cos theta + isin theta)) then sin^(-1) x = |
|
Answer» `(pi)/(3)` |
|
| 9645. |
Evaluation of definite integrals by subsitiution and properties of its : int_(-(pi)/(6))^(pi/6)sin^(5)xcos^(2)xdx=........... |
|
Answer» `(1)/(sqrt2)-1` |
|
| 9646. |
Statement -I: If alpha gtbeta gt 1, then (alpha^(sqrt(log_(alpha)beta)))/(beta^(sqrt(log_(beta)alpha))) is greater than 1. Statement-2 : log_(c) b = (log_(a)b)/(log_(a)c), if 0lt a,b,cne1. |
|
Answer» STATEMENT -1 is ture, statement -2 is ture and statement-2 is CORRECT explaination for statement -1 |
|
| 9647. |
The mid points of the sides of a triangle are (5, 0), (5, 12) and (0, 12). The orthocentre of this triangle is |
| Answer» Answer :A | |
| 9650. |
If m_1 and m_2 are the roots of the equation x^2+(root()3+2)x+(root()3-1)=0 then the area of the triangle formed by the lines y=m_1x, y=m_2x and y=c |
|
Answer» `((root ()33-root ()11)/4).c^2` |
|