Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

10951.

A tetrahedron is three dimensional figure bounded by four non coplanar triangular plane. So a tetrahedron has points A,B,C,D as its vertices, which have coordinates (x_(1),y_(1),z_(1)) (x_(2), y_(2), z_(2)) , (x _(3), y_(3) , z_(3)) and (x _(4), y _(4), z _(4)) respectively in a rectangular three –dimensional space. Then the coordinates of its centroid are ((x_(1)+ x_(2) + x _(3) + x_(4))/(4) , (y _(1) + y _(2) + y_(3) + y _(4))/(4), (z_(1) + z_(2) + z_(3)+ z_(4))/(4)). The circumcentre of the tetrahedron is the centre of a sphere passing through its vertices. So, the circumcentre is a point equidistant from each of the vertices of tetrahedron. Let tetrahedron has three of its vertices represented by the points (0,0,0) ,(6,-5,-1) and (-4,1,3) and its centroid lies at the point (1,-2,5). Now answer the following questions The distance between the planes x + 2y- 3z -4 =0 and 2x + 4y - 6z=1 along the line x/1= (y)/(-3) = z/2 is :

Answer»

`19/22`
`(7 SQRT7)/(22)`
`(7)/(22)`
`(7 SQRT14)/(22)`

ANSWER :D
Discussion
10952.

A line segment of length 8cm is divided into two parts AP and PB by a point P. If AP^2+PB^2 is minimum then AP=

Answer»

P is the midpoint of AB
P is a point of TRISECTION of AB
P divides AB in the RATIO 1:3
none

Answer :A
Discussion
10953.

Evalute the following integrals int (x^(3m) + x^(2m) + x^(m)) (2x^(2m) + 3x^(m) + 6)^((1)/(m))dx ( x gt 0) (m in^(x) N)

Answer»


Answer :`(1)/(6 (m +1)) [ 2x^(3m) + 3X^(2M) + 6x^(m) ]^(m + 1//m) ` + C
Discussion
10954.

int_(-1)^(3/2) | x sin (pi x ) | dx =

Answer»


ANSWER :`(3)/(PI) + (1)/(pi^(2))`
Discussion
10955.

Evaluate int _(0)^(pi//2)ln((1+a sin x)/(1- a sin x)) (dx)/(sinx) (|a|lt1)

Answer»


ANSWER :`=PI^(-1) a +C`
Discussion
10956.

Consider three distinct real numbers a,b,c in a G.P with a^2+b^2+c^2=t^2 and a+b+c =alpha t .The sum of the common ratio and its reciprocal is denoted by S. Complete set of alpha^2 is

Answer»

`(1/3,3)`
`[1/3,3]`
`(1/3,3)-{1}`
`(-oo,1/3)cap (3,oo)`

Solution :a,b,c are in G.P. HENCE,a,ar,`ar^(2)` are in G.P. So,
`(a^(2)+a^(2)R^(2)+a^(2)r^(4))/((a+ar+ar^(2))^(2))=t^(2)/(alpha^(2)t^(2))=1/alpha^(2)`
`alpha^(2)=(r^(2)+r+1)/(r^(2)-r+1)`
LET `alpha^(2)=y`,
`thereforey=(r^(2)+r+1)/(r^(2)-r+1)`
`(y-1)r^(2)-r(y+1)+(y-1)=0`
For REAL r,
`(y+1)^(2)-4(y-1)^(2)ge0`
`rArr1/3leyle3`
But `ne1//3,1,3``(becauserne1,-1,0)`
`therefore1/3ltylt3andyne1`
`alpha^(2)in(1/3,3)-{1}`
Discussion
10957.

Consider three distinct real numbers a,b,c in a G.P with a^2+b^2+c^2=t^2 and a+b+c =alpha t .The sum of the common ratio and its reciprocal is denoted by S. Complete set of alpha^2 is

Answer»

`(-2,2)`
`(-oo,-2) cup (2,oo)`
`(-1,1)`
`(-oo, -1)cup (1,oo)`

Solution :`S=r+1/r`
`SIN(-oo,-2)cup(2,oo)`
Discussion
10958.

Show that the least cloth is required to construct a conical tent of given volume if the ratio of height to the base radius is sqrt2 : 1.

Answer»
Discussion
10959.

If the foot of perpendicular drawn from the point (a,b,c) and the line x = y = z then .....

Answer»

R = a + b + C
r= 3(a+b+c)
3R = a + b + c
r=abc

Answer :C
Discussion
10960.

Which of the following operations is not possible ?

Answer»

`(vecA.VECB)VECC`
`((vecA.vecB))/((vecA.vecC))`
`(vecA.vecC)/vecB`
`vecB/(vecA.vecC)`
Discussion
10961.

If P = (0,1,0), Q = (0,2,1) , then the projection of PQ on the planex+y + z = 3 is

Answer»

2
`SQRT(2)`
3
`sqrt(3)`

ANSWER :B
Discussion
10962.

1+(1+2)/(2!) +(1+2 +2^2)/(3!) + .......oo =

Answer»

`E(e-1)`
`(e(e-1))/2`
`(e(e^2-1))/2`
`(e(e-1))/4`

ANSWER :A
Discussion
10963.

If 2P(A) = P(B) =5/13 and P(A/B) = 2/5 find P(AcupB)

Answer»


ANSWER :`11/26~~0.42`
Discussion
10964.

Draw the graph of y=(1-x^(2))/(1+x^(2)) and hence draw the graph of y=cos^(-1).(1-x^(2))/(1+x^(2)).

Answer»

Solution :We have `y=f(x)=(1-x^(2))/(1+x^(2))=(2)/(1+x^(2))-1`
Clearly, the domain is R.
`y=f(x)` is an even funtion, so the graph is SYMMETRICAL about the y-axis.
Let us first draw the graph of r`x in [0,oo)`.
`f(0)=1`
`f(x)=0 :. x=1`
`underset(xrarroo)lim((2)/(1+x^(2))-1)=-1`
THUS, from `f(0)=1,((2)/(1+x^(2))-1)` decreases intersecting the x-axis at (1,0) and APPROACHES '-1' as x approaches `'oo'`.
Also `f'(x)=(-4X)/((1+x^(2))^(2))`, so f(x) is differentiable at x = 0.
Hence the graph of `y=f(x)` is as shown in the FOLLOWING figure.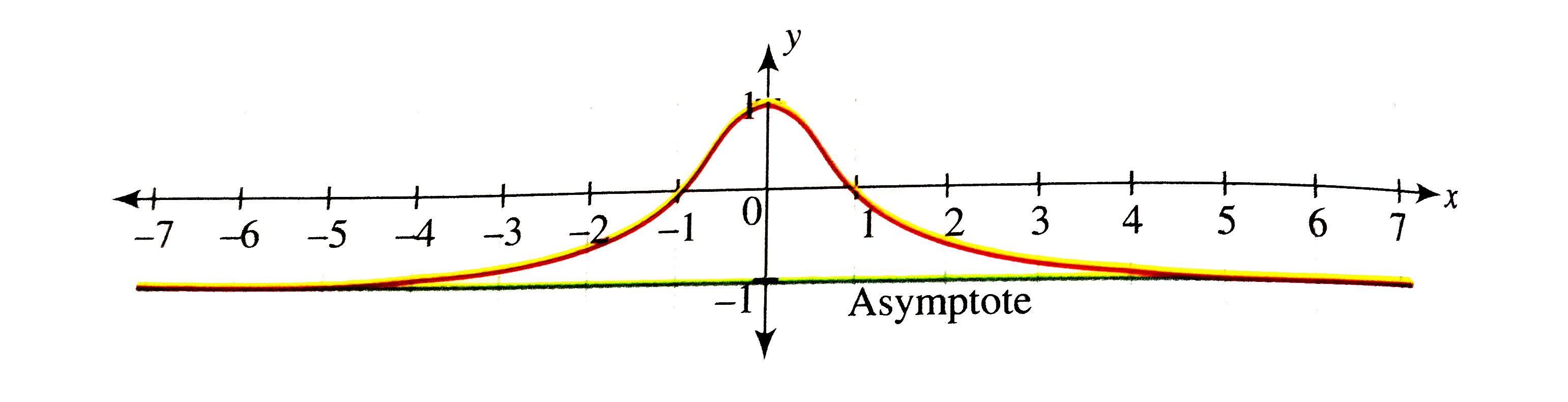

Since the range of `(1-x^(2))/(1+x^(2))` is (-1,1), the domain of `g(x)=cos^(-1)f(x)=cos^(-1).(1-x^(2))/(1+x^(2))` is also R
`g(0)=cos^(-1)(1)=0`
and `underset(xrarroo)limcos^(-1)((1-x^(2))/(1+x^(2)))=underset(xrarroo)lim cos^(-1)((2)/(1+x^(2))-1)=pi`
Thus, the value of g(x) increases from '0' and approaches `'pi'` as x approaches `'oo'`.
Also g(x) is an enven function, so the graph is symmetrical about the y-axis.
Also `g'(x)=(f'(x))/(sqrt(1-(f(x))^(2)))`
g'(0) does not exist as f(0)=1, so g(x) is non-differentiable at x=0.
Hence the graph of `y=g(x)` can be drawn as shown in the following figure.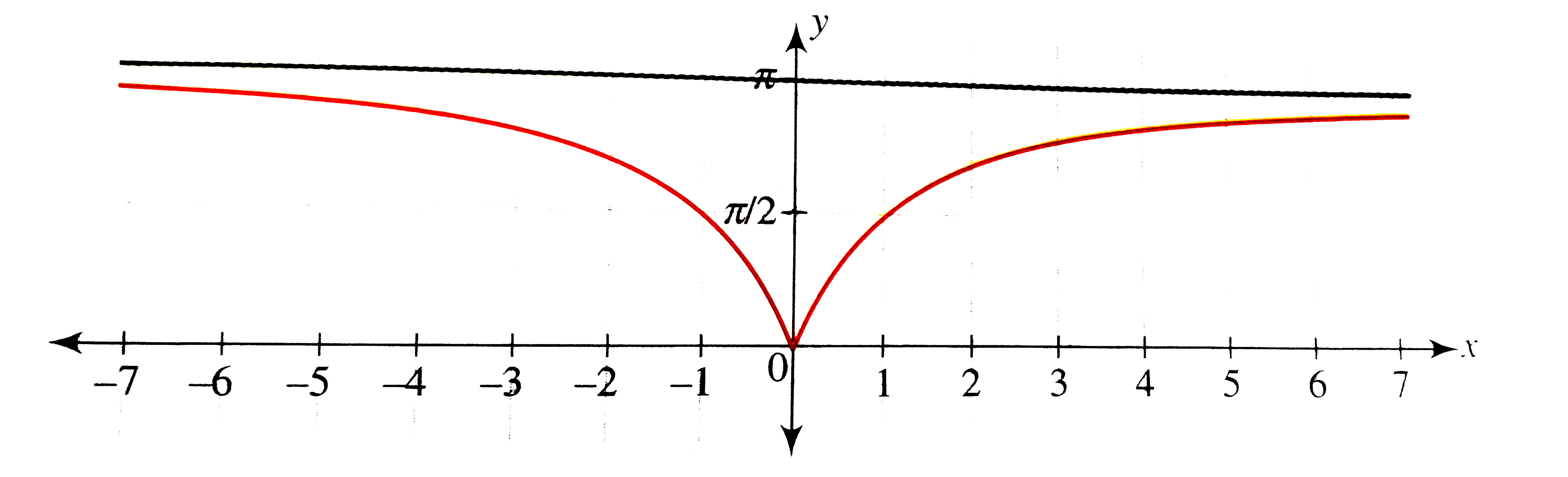
Discussion
10965.

|adjA|=|A|^2 , where A is a square matrix of order two

Answer»


ANSWER :FALSE
Discussion
10966.

Prove that the curves x=y^(2) and xy = k cuts at right angles if 8k^(2)=1.

Answer»


ANSWER :1
Discussion
10967.

A book containing 100 pages is opened at random. The probability that on that page a doublet is found is

Answer»

`(1)/(10)`
`(9)/(101)`
`(9)/(100)`
`(1)/(11)`

ANSWER :C
Discussion
10968.

If tan^(-1)x+ tan^(-1)y+tan^(-1)z=pi/2, then 1-xy-yz-zx is equal to

Answer»

1
0
`-1`
2

Answer :B
Discussion
10969.

The probability that a bulb produced by a factory will fuse after 150 days of use is 0. 05. find the probability that out of 5 such bulbs.i. none ii. not more than oneiii. more than one iv. atleast one will fuse after 150 days of use.

Answer»


ANSWER :i. `(0.95)^(5)`ii. `(0.95)^(4) xx 1.2`,iii. `1-(0.95)^(4) xx 1.2` and IV. `1-(0.95)^(5)`
Discussion
10970.

Two circles S and S' intersect at P and Q. A, C lie on S and B , D lie n S' such that APB is parallel to CQD . Then

Answer»

ABCD is CYCLIC quadriateral
AC is parallel to BD
ABCD is a RECTANGLE
`angle ACQ = 90^(@)`

ANSWER :B
Discussion
10971.

If 2f(x) = f'(x) and f(0) = 3 then f(2) =

Answer»

`4e^(3)`
`3E^(4)`
`2e^(3)`
`3e^(2)`

ANSWER :B
Discussion
10972.

If then sum of two positive numbers in constant then show that their product is maximum when they are equal.

Answer»

SOLUTION :Let X and y be two positive numbers such that x + y = C (constant)
then y = c - x
Let `p = xy = x(c- x) = cx - x^2`
`dp/dx = c - 2x, (d^2p)/dx^2 = - 2 lt 0`
`therefore` p is maximum when `c - 2x = 0 I.e, x = c/2`
if `x= c/2` then `y=c/2`.
`therefore` The two numbers are equal. (Proved)
Discussion
10973.

From a piont P (0,b) two tangents are drawn to the circle x^2+y^2=16 and these two tangents intersect X-axix is two points A and B. If the are of DeltaPAB is minimum , then the equation of its circumcircle is

Answer»

`x^2+y^2=6 sqrt(2)`
`x^(2)+y^(2)=64`
`x^2+y^2=32`
`x^2+y^2=4sqrt(2)`

ANSWER :C
Discussion
10974.

If (1+x+x^(2))^(8)=a_(0)+a_(1)x+a_(2)x^(2)+.........+a_(16)x^(18)AAx " then "a_(5), us equal to……….

Answer»

502
804
506
508

Solution :`F'(X)=0" for " x=-1`
Discussion
10975.

If the chord y=mx+1 of the circle x^(2)+y^(2)=1 subtends an angle of measure 45^(@) at the major segment of the circle then m=

Answer»

0.02
`-1`
`-2`
`3`

ANSWER :B
Discussion
10976.

Consider following data 35,32,36,34,41,45,28,50,49 I . Find the median (ii)Find the mean deviation from the median.

Answer»


ANSWER :`=6.22`
Discussion
10977.

Let A = [(1,tanx),(-tanx, 1)] & B = A^(T) A^(-2) if f(x) = det (adj B) then number of solution(s) of the equation 10f(x) – x = 0 is (are) [Note: det(P) denotes the determinant of a square matrix P]

Answer»


Solution :`f(X) = DET (adj)(B)) = |adj (B)| = |B|`
` = |A^(T)||A^(-2)| = |A| 1/(|A|^2)`
`=1/(|A|) = 1/("sec"^2 x) = cos^(2) x`

`10 cos^(2) x - x = 0`
Discussion
10978.

Integrate the following int_0^1x^7/sqrt(1-x^2)dx

Answer»

Solution :`int_0^1x^7/sqrt(1-x^2)DX`
=`int_0^(pi/2)(sin^7theta.costhetad theta)/costheta (where `x=sintheta`
`rArr dx=costhetad theta`)
=`int_0^(pi/2)sin^7thetad theta=6/7 . 4/5 . 2/3=(48)/105`
Discussion
10979.

Show that (i) (3+isqrt(5))^(12)+(3-isqrt(5))^(12) is real and (ii) ((13-i)/(5-3i))^(15)-((7+4i)/(2+3i))^(15) ia purely imaginary.

Answer»


Answer :`(i)z` is REAL
`(II) z` is PURELY IMAGINARY.
Discussion
10980.

If A and B are two square matirces of the same order , then A+B=B+A.

Answer»


ANSWER :1
Discussion
10981.

Derive the expression for the volume of the prallelopiped whose coterminus edges are vectors bar(a),bar(b),bar(c).

Answer»

SOLUTION :LET `bar(OA),barOBandbar(OC)` represent the coterminus edges `bar(a),bar(b)andbar(c)` respectively of the parallelopiped. Draw seg AN perpendicular to the PLANE of `bar(b)and bar(c)`.
Let `theta` be the angle between `bar(b)andbar(c)andphi` be the angle between the line line AN and `bar(a)`.
If `hat(n)` is the unit vector perpendicular to the palne of `bar(b)andbar(c)`, then the angle between `bar(a)andbar(c)`, then the angle between `bar(a)andhat(n)` is also `phi`.
Volume of the parallelopiped
= (area of parallelogram OBA'C) `xx` AN
`=(bcsintheta)(acosphi)`
`=a(bcsintheta)(cosphi)`. . . (1)
Now let us consider the scalar TRIPLE produst `bar(a)*(bar(b)xxbar(c))`
`bar(b)xxbar(c)=(bcsintheta)*hat(n):.|bar(b)xxbar(c)|=bcsintheta`
`:.bar(a)*(bar(b)xxbar(c))=|bar(a)|*|bar(b)xxbar(c)|cosphi=a(bcsintheta)cosphi`. . . (2)
`:.` from (1) and (2),
volume of the parallelopiped `=bar(a)*(bar(b)xxbar(c))`
Discussion
10982.

If A(n) represent the area bounded by the curve y=n " lnx "("where "n in N" and " n gt1) and x-axis from x=1 to x=e, then value of A(n)+nA(n-1) is equal to

Answer»

`n^(2)`
`en^(2)`
`n^(2)/(e+1)`
`n^(2)/(e-1)`

Solution :`A(n)=underset(1)overset(e)(INT)n"LN "xdx=n`
`thereforeA(n)+NA(n-1)=n+n(n-1)=n^(2)`
Discussion
10983.

Sketch the curve y=f(x)=x^(3)-6x-9

Answer»


ANSWER :`(0,F(0))=(0,9)`
Discussion
10984.

If f(x) is continuous on [0,2] , differentiable in (0,2) ,f(0)=2, f(2)=8 and f.(x) le3 for all x in (0,2), then find the value of f(1).

Answer»

4
5
6
7

Solution :Applying LMVT to f in [0,1] and again in [1,2] there exists `C_1 in (0,1)` such that
`(f(1)-f(0))/(1-0) = f.C_1 1 le 3 RARR f(1) le 5` …(i)
There exists `C_2 in (1,2)`, such that
`(f(2)-f(1))/(2-1) = f.(C_2) le 3 rArr f(1) GE 5`
Hence, (1) and (2) imply that f(1)=5
Discussion
10985.

Integrate the following intsec^2sqrtx/sqrtxdx

Answer»

SOLUTION :`intsec^2sqrtx/sqrtxdx`
PUT`SQRTX=z`then `(1/2sqrtx)DX=DZ` or `dx/(sqrtx)=2dz`
`intsec^zcdot2 dz`
2tanz+C
`2tansqrtx+C`
Discussion
10986.

Let x^(2) - ( m - 3) x + m = 0 ( m in R) be a quadratic equation. Find the value of m for which the roots are (i) real and distinct (ii) equal (iii) not real (iv) oppsite in sing (v) equal in magnitude but opposite in sing (vi) positive (vii) negative (viii) such that at least one ispositive (ix) one root is smaller than 2 and the other root is greater then 2 (x) both the roots are grater then 2 (xi)both the roots are smaller then 2 (xii) exactly one root lies in the interval ( 1, 2) (xiii) both the roots lie in the interval (1, 2) (xvi) at least one root lies in the interval (1, 2) (xv) one root is greater than 2 and the other root is smaller than 1

Answer»

Solution :Let`f(X)= x^(2)- m ( m - 3) x + m = 0`
(i) Both the roots are real and DISTINCT. So, `D gt`0
`rArr(m - 3)^(2) - 4m gt ` 0
or`m^(2) - 10m + 9 gt`0
or`(m -1) (m - 9) gt` 0
`rArrm in (-infty, 1 ) cup (9, infty)`

(ii) Both the roots are equal. So
`D= 0`
`rArrm = 9 or m = 1`

(iii) Both the roots are imaginary. So,
`D lt`0
`rArr( m - 1)(m - 9) lt` 0
`rArrm in` ( 1, 9)

(iv) The roots are oppsite in sing . Hence, the product of root is negative. So,
`m lt rArrm in (-infty, 0)`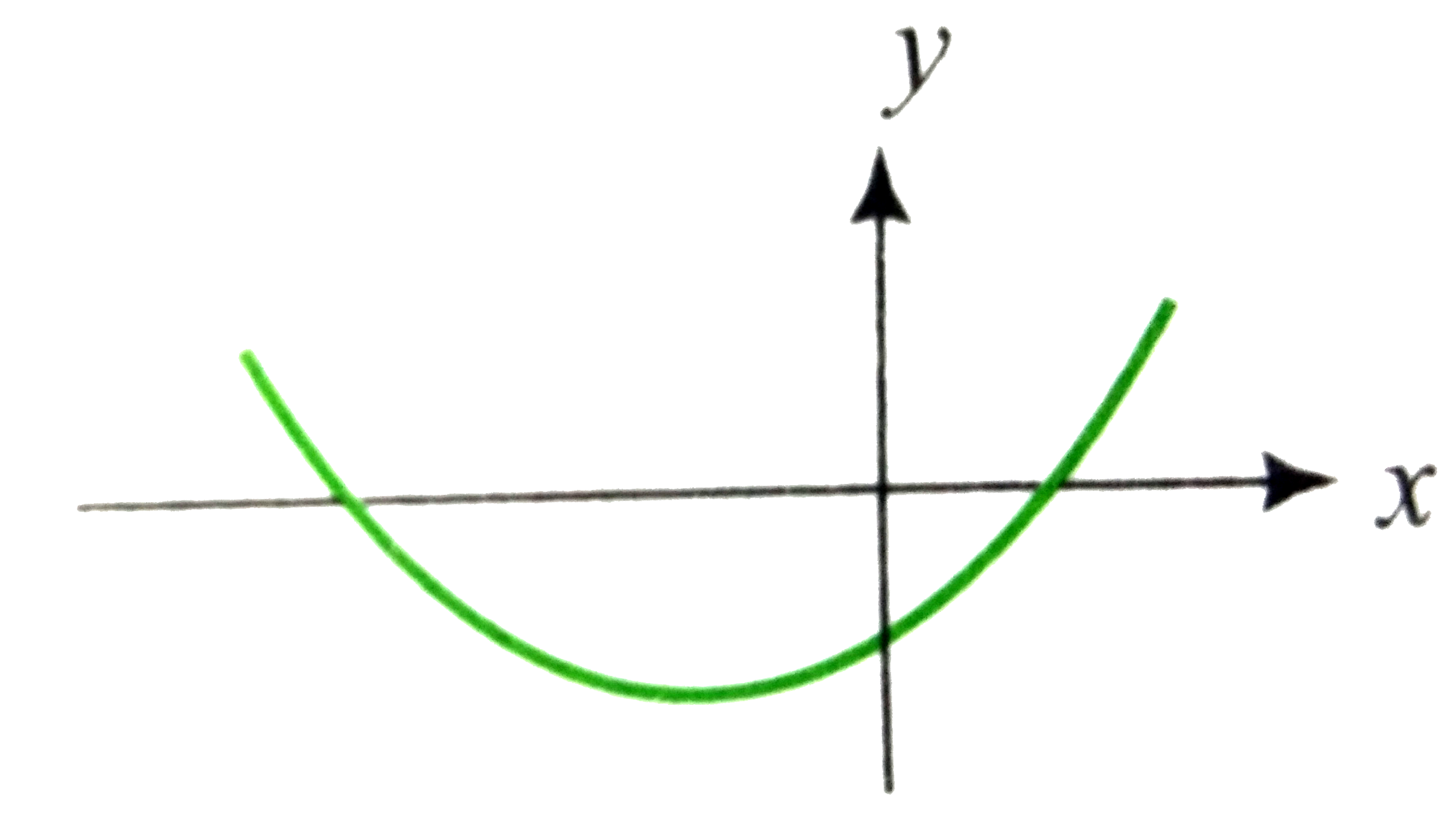

(v)Roots are equal in magnitude but opposite in sign . Hence, SUM of roots is zero as well asD`ge 0. ` So,
m `in (-infty,1) cup (9, infty)`
and`m - 3 = 0, i.e., m = 3`
Hence, so such m exists.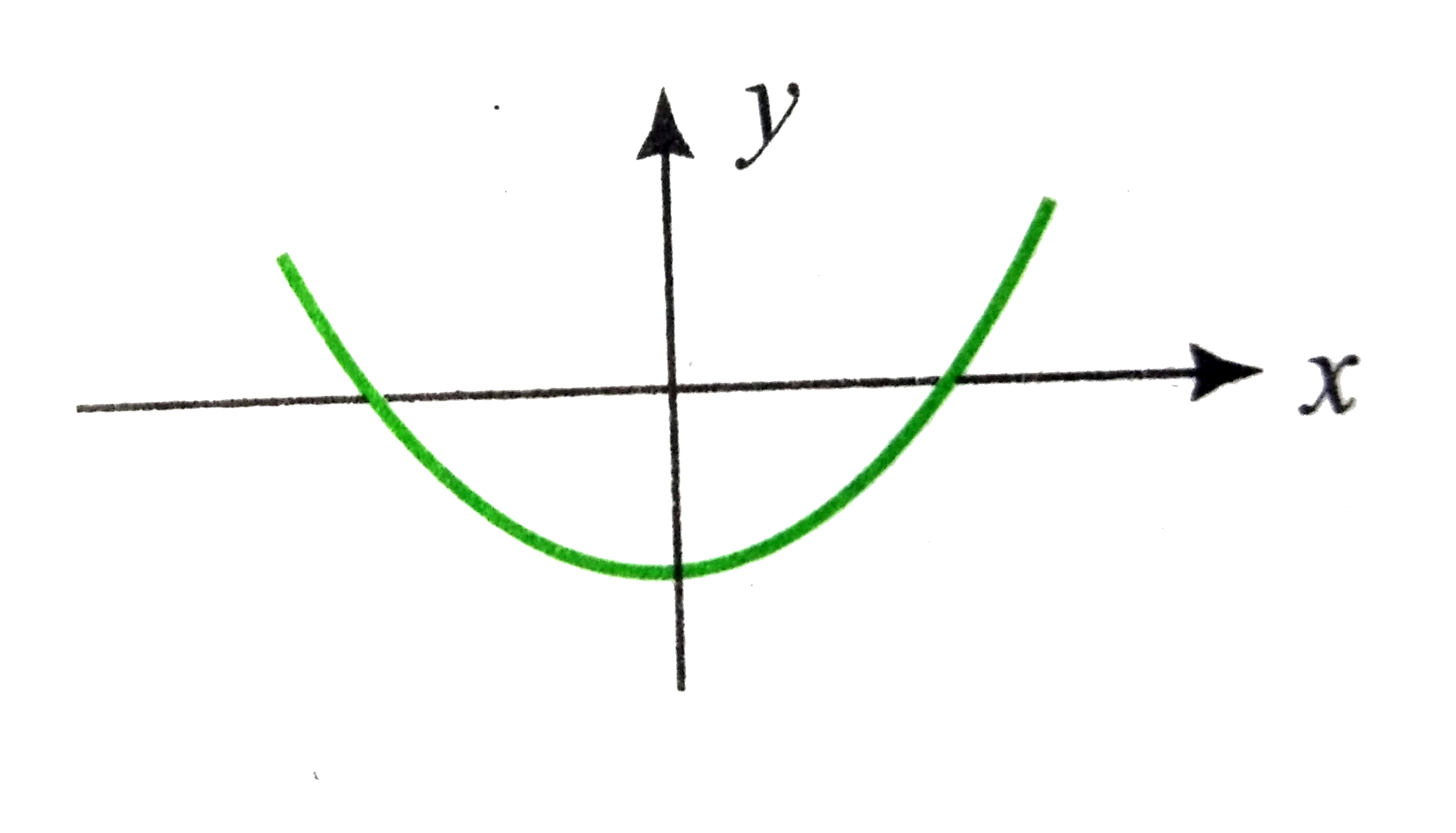

(vi)
Both the roots are positive. Hence, `D lt ` 0, and both the sum and the product of roots are positive. So,
m - 3`gt 0, m gt` 0and m `(-infty, 1] cup [9, infty)`
m `in [ 9, infty)`
(vii)
At least one root is positive . Hence, either one rootis positive or both roots are positive . So,
m`in (-infty, 0) cup [9, infty)`
(ix)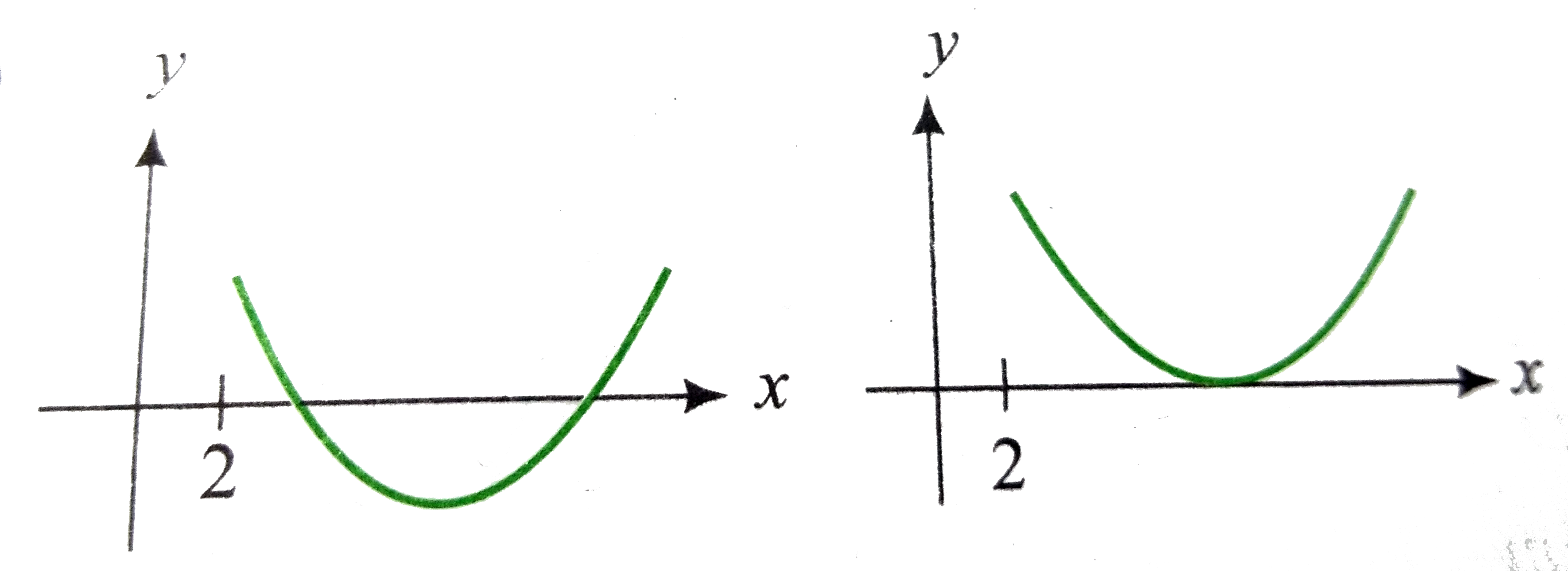
One root is smaller then 2 and the other root is greater than 2, i.e., 2 lies between the roots. So,
`f(2) lt` 0
`rArr4 -2 (m - 3) + m lt` 0
`rArrm gt ` 10
(x)
Both the roots are greater then 2. So,
`f(2) gt 0, D ge 0, - (b)/(2A) gt` 2
`rArrm lt` 10 and m `in ( - infty, 1] cup [9, infty)` and m - 3 `gt`4
`rArrm in` [ 9, 10)
(xi)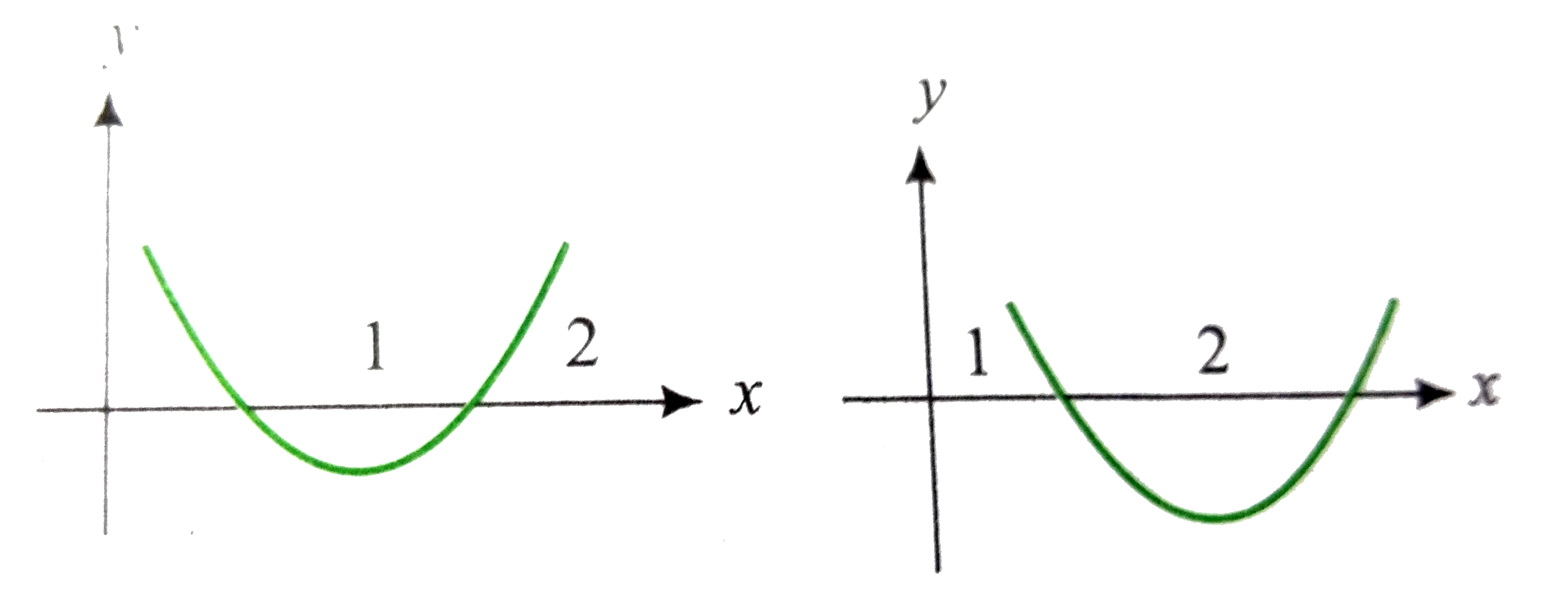
Both the roots are smaller then 2. So,
`f(2) gt 0, ge 0, - (b)/(2a) lt` 2
`rArrm in (-infty, 1]`
Exactly one root lies in (1, 2) . So,
`f(1) f(2) lt` 0
`rArr4(10 - m ) lt` 0
`rArrm in (10, infty)`
(xiii) Both the roots lie in the interval (1, 2) . Then,
D `ge 0 rArr(m - 1) (m - 9) ge` 0
`rArrm LE 1 or ge `9(1)
Also `f(1) gt `0 and `f(2) gt 0 rArr10 lt ` m(2)
and`1lt-(b)/(2a) lt 2 rArr 5 lt m lt 7`(3)
Thus, no such m exists.
(xvi)Cace I : Exactly one root lies in (1, 2 ). So,
`f(1)f(2) lt 0 rArrm gt `10
Case II: Both the roots lie in (1, 2). S0, from (xiii),
m `in phi`. Hence, m `in (10, infty`).
For one root greater than 2 and the other root smaller than 1,
`f(1)lt` 0 and `f(2) lt` 0
But `f(1) = 4. Thus, no such m exists.
Discussion
10987.

lim_(n to oo)(1)/(n)[tan.(pi)/(4n)+tan.(2pi)/(4n)+…..+tan.(n pi)/(4n)]

Answer»

log 2
`(2)/(PI) log 2`
`(1)/(pi) log 2`
`(3)/(pi) log 2`

ANSWER :B
Discussion
10988.

Two tangents to the hyperbola (x^(2))/(25) -(y^(2))/(9) =1, having slopes 2 and m where (m ne 2) cuts the axes at four concyclic points then the slope m is/are

Answer»

`-(1)/(2)`
`-2`
`(1)/(2)`
2

Solution :Tangents having slope `'2', y = 2X +- sqrt(100-9) = 2x +- sqrt(91)`
It meets the axis at `A -= (+-(sqrt(91))/(2),0),B (0,+-sqrt(91))`
Tangents having slope `'m', y = MX+- sqrt(25 m^(2)-9)`
It meets the axis at `D(+-(sqrt(25m^(2)-9))/(m),0), C -= (0,+-sqrt(25m^(2)-9))`
ABCD is cyclic quadrilateral
`rArr OA XX OD xx OB xx OC`
`rArr (sqrt(91)(sqrt(25m^(2)-9)))/(2m) =sqrt(91) (sqrt(25m^(2)-9))`
`rArr 2m = 1 rArr m= (1)/(2)`
Discussion
10989.

For some constant a and b, find the derivative of i. (x-a)(x- b)ii. (ax^(2)+b)^(2) iii. (x-a)/(x-b)

Answer»


ANSWER :i. `2x-a-b` ii. `4AX(AX^(2)+b)`iii. `(a-b)/((x-b)^(2))`
Discussion
10990.

Find (dy)/(dx) in the following sin^(2)x + cos^(2)y=1

Answer»


ANSWER :`(SIN 2X)/(sin 2Y)`
Discussion
10991.

If C is the mid-point of AB and P is any point outside AB, then

Answer»

PA + PB = PC
PA + PB + 2 PC = 0
PA + PB - 2PC = 0
PA + PB + PC = 0

Solution :By the PROPERTIES of mid-point THEOREM,
PA + PB = 2 PC
Discussion
10992.

Let y=x^(3)-8x+7 and x=f(t) given t=0, x=3 Find the value of (dx)/(dt)

Answer»

`(2)/(19)`
`(-2)/(19)`
`(19)/(2)`
`(-19)/(2)`

ANSWER :A
Discussion
10993.

Find the derivative of f given by f(x)= tan^(-1)x assuming it exists

Answer»


ANSWER :`(1)/(1 + X^(2))`
Discussion
10994.

Standard deviation of first 'n' natural numbers is

Answer»

`(N+1)/(2)`
`SQRT((n(n+1))/(2))`
`sqrt((n^(2) - 1)/(12))`
n

Answer :C
Discussion
10995.

If A=[{:(cosalpha,sinalpha),(-sinalpha,cosalpha):}],andA^(-1)=A', find value of alpha.

Answer»


ANSWER :`AAalpha INR`.
Discussion
10996.

Fundamental theorem of definite integral : If int_(sinx)^(1)t^(2)f(t)dt=(1-sinx) then f((1)/(sqrt3))=........

Answer»

`(1)/(3)`
`(1)/(SQRT3)`
3
`sqrt3`

ANSWER :C
Discussion
10997.

If [[3y-x,-2x],[3,7]] = [[5,-2],[3,7]],then find x and y

Answer»

`2,1`
`1,2`
`2,3`
`1,3`

ANSWER :B
Discussion
10998.

If lt 1then (1-2x)/(1 - x x ^(2)) + ( 2x - 4x ^(3))/(1 - x ^(2) + x ^(4)) + (4x^(3) - 8x ^(7))/(10 x ^(4) + x ^(8)) + …oo=

Answer»

`(1+ 2X)/(1 + 1+ x ^(2))`
`(1-2x)/(1 + x + x ^(2))`
`((1+ 2x )^(2))/(1 + x+ x ^(2))`
`((1+ 2x ) ^(3))/(1+ x+ x ^(2))`

Answer :A
Discussion
10999.

If x is real, the minimum value of x^(2)-8x+17 is …………. (Where x in R)

Answer»

`-1`
0
1
2

Answer :C
Discussion
11000.

If ax + by + c = 0 is the polar of (1,1) with respect to the circle x^(2) + y^(2) - 2x + 2y + 1 = 0 and H. C. F. of a, b, c is equal to one then find a^(2) + b^(2) + c^(2) .

Answer»


ANSWER :`5`
Discussion