Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

27901.

You say the code word, and the door opens. You walk in, and look around the empty room. It is a dead end, but you see a poem on the wall. It reads: As you dance each _______around, through once, once only, Me, when you shallhave found, do not hide your glee ! One of you notices that the code word fits in the blank of the poem. As you think about the poem, you see an arrow which directs your eyes downward. To your amazement, you find the whole floor filled with letters and symbols! You realize that you need to use the poem to find a solution to the puzzle under them. The floor looked like this: Rearrange the clues from the puzzle above, using the poem, to find a question and then answer it to get out of the cave. What is the answer which can take you out of the cave?

Answer»

7
70
18
81

Solution :D
After decoding the poem, you REALIZE that you must go around ‘H’ in the MATRIX in the direction GIVEN by arrow and note down the word formed. On FINDING out all such words and combining the you will GET the following question
squre/of/largest/one/digit/number/
So, theanswer is `=9^(2) =81 `
Discussion
27902.

Find the value of the integral underset(0)overset(2)int x^(3//2)sqrt(2-x) dx

Answer»


ANSWER :`(PI)/(2)`
Discussion
27903.

Match the following {:(,"Column-I",,"Column-II",),((A),"If A and B are otthogonal, then AB is",(p),"Zero matrix",),((B),"If A and B are nilpotent matrices of order r and s and A and B commute, then "(AB)^(r)"is",(q),"Nilpotent matrix",),((C),"If A is a hermitian matrix such that "A^(2)=0", then A is ",(r),"Unitary matrix",),((D),"If A and B are unitary matrices, then AB is",(s),"Orthogonal",):}

Answer»

<P>

Answer :A(s), B(p,q), C(p,q),D(R )
Discussion
27904.

Given two independent events A and B such that P(A)=0.3,P(B)=0.6. find P(neither A nor B)

Answer»

<P>

SOLUTION :GIVEN that P (A) = 0.3 and P(B) = 0.6therefore `P(A^c)`= 1-P(A) = 1-0.3=0.7
`P(B^c)` = 1-P(B) = 1-0.6=0.4
=`P(A^cnnB^c)=P(A^c) P(B^c)`
=`0.7xx0.4`=0.28
Discussion
27905.

{:("Column A","x is a two digit number. The digits of the number differ by 6, and the squares of the digits differ by 60" ,"Column B"),(x , ,60):}

Answer»

If COLUMN A is larger
If column B is larger
If the COLUMNS are equal
If there is not ENOUGH information to decide

Answer :D
Discussion
27906.

Evalute the following integrals int (2x^(3))/(1 + x^(8)) dx

Answer»


Answer :`(1)/(2)TAN^(-1)(X^(4))+C`
Discussion
27907.

i Reduce the equation 3x + 4y - 12 = 0 into intercept form. ii. Find the distance of the above line from the origin. iii. Find the distance of the above line from the line 6x + 8y- 18 = 0.

Answer»


ANSWER :i. `(X)/(4)+(y)/(3)=1`, ii. `(12)/(5)`, iii. `(3)/(5)`
Discussion
27908.

If sinA+sinB=l and cosA-cosA-cosB=m, then cos(A-B)=

Answer»

`(L^(2)-m^(2))/(l^(2)+m^(2))`
`(l^(2)+m^(2))/(l^(2)-m^(2))`
`(2LM)/(l^(2)+m^(2))`
`(2lm)/(l^(2)-m^(2))`

ANSWER :A
Discussion
27909.

Let f(x)= int_(x)^(x+(pi)/(3))|sin theta|d theta(x in [0,pi])

Answer»

`f(x)` is stricity increasing inthis interval
`f(x)` is DIFFERENTIABLE in this interval
Range of `f(x)` is `[2-sqrt(3)-1]`
`f(x)` has a maxima at `x = pi/3`

SOLUTION :N//A
Discussion
27910.

Findthe valueofsin^(-1)( sin "" (5pi)/(9 )cos "" (pi)/(9) + cos""(5 pi )/(9)sin""(pi) /(9))

Answer»


ANSWER :`(PI)/(3)`
Discussion
27911.

If (1!)^(2) + (2!)^(2) + (3!)^(2) + "…….." + (99!)^(2) is divided by 100, the remainder is

Answer»

27
28
17
14

Answer :C
Discussion
27912.

C_0 + (C_1)/(2) + (C_2)/(2^2) + (C_3)/(2^3)+…..+(C_n)/(2^n)=

Answer»

`(2^(n+1)-1)/(n+1)`
`(2^n -1)/(n+1)`
`(2^n)/(n+1)`
`(1)/(n+1)`

ANSWER :B
Discussion
27913.

The value of (1)/(i)+(1)/(i^2)+(1)/(i^3)+"……"+(1)/(i^(102) is equal to

Answer»

`-1-i`
`-1+i`
`1+i`
`1-2i`

ANSWER :A
Discussion
27914.

An ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is tan^(-1)(2sqrt(2)), then find the ecentricity of the ellipse

Answer»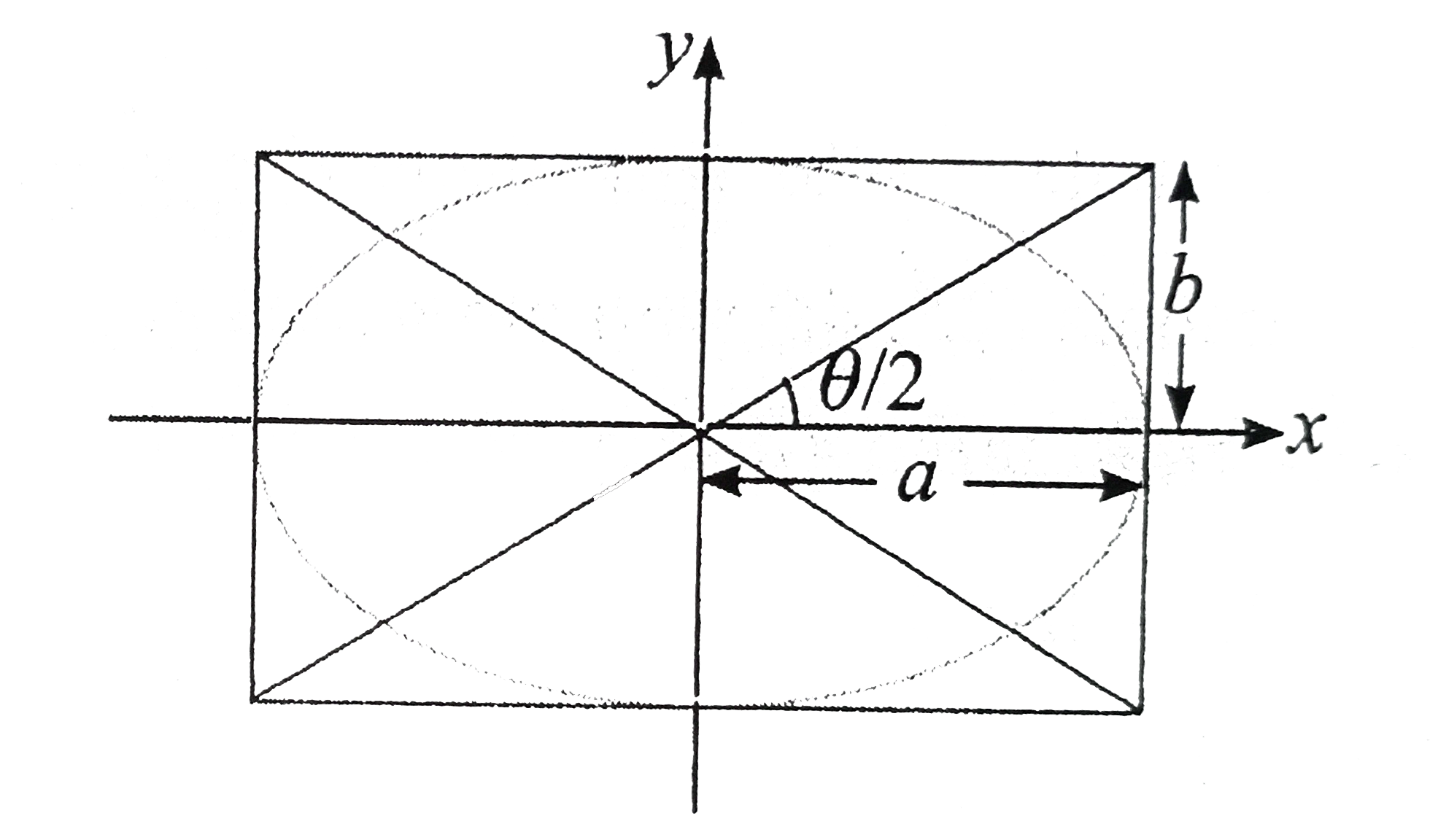


Solution :
From the FIGURE, we have
`TAN.(THETA)/(2)=(b)/(a)rArrtan^(2).(theta)/(2)=(b^(2))/(a^(2))`
`rArr(1-costheta)/(1+cos theta)=(b^(2))/(a^(2))`
`rArr(1-(1)/(3))/(1+(1)/(3))=(b^(2))/(a^(2))rArr(b^(2))/(a^(2))=(1)/(2)`
`:. e=sqrt(1-(b^(2))/a^(2))=(1)/(sqrt(2))`
Discussion
27915.

Between 4 and 2916 are inserted off number (2n +1) G.M's.Then the (n +1)th G.M. is

Answer»


ANSWER :108
Discussion
27916.

Find the equation of circle which intersect the circle x^2+y^2-6x+4y-3=0 orthogonallyand passes throughthe point (3,0) and touches Y-axis.

Answer»


ANSWER :`x^2+y^2-6x-6y+9=0`
Discussion
27917.

If the normal to the curve x^(3) = y^(2) at the point (m^(2), -m^(3)) is y = mx - 2m^(3), then the value of m^(2) is

Answer»

1
`1//2`
`1//3`
`2//3`

ANSWER :D
Discussion
27918.

An experiment succeeds twice as often as it fails. The probability of at least 5 successes in the six trials of this experiment is

Answer»

`(496)/(729)`
`(192)/(729)`
`(240)/(729)`
`(256)/(729)`

ANSWER :D
Discussion
27919.

Equation of the plane passing through point P(a,b,c) and perpendicular to OP is

Answer»

`ax+by+cz=a+b+c`
`ax+by+cz=a^2+b^2+c^2`
`(X)/(a)+(y)/(b)+(z)/(c )=3`
`ax+by+cz=(a+b+c)^2`

Answer :B
Discussion
27920.

If alpha, beta , gamma are the roots of the equation x^(3)-x^(2) + 4=-0, then form an equation where roots are alpha + beta^(2) + gamma^(2), beta = alpha^(2) + gamma^(2), gamma + alpha^(2) + beta^(2)

Answer»


ANSWER :`X^(3) - 3X^(2) -x+19`
Discussion
27921.

int_(0)^(1)x(1-x)^(n)dx=

Answer»

`(1)/(n+1)-(1)/(n+2)`
`(1)/(n+1)+(1)/(n+2)`
`(1)/(n+2)`
`(1)/(n+2)`

ANSWER :A
Discussion
27922.

A psychologist's experiment involved timing 15 small children as they found the solution to a little puzzle . Each child received at least one similar puzzle to play with before being timed . The scatterplot below shows the time each child took to solve the puzzle , and the corresponding number of "practice" puzzles each child received . On the basis of these data ,which of the following functions best models the relationship between t, the number of minutes taken to complete the puzzle , and p , the number of practice puzzles ?

Answer»

<P>t(p)=9
`t(p)=p/2+9`
`t(p)=-p/2+9`
`t(p)=-p/2`

ANSWER :B
Discussion
27923.

If alpha,betane0 and f(n)=alpha^(n)+beta^(n) and |(3,1+f(1),1+f(2)),(1+f(1),1+f(2),1+f(3)),(1+f(2),1+f(3),1+f(4))| =k(1-alpha)^(2)(1-beta)^(2)(alpha-beta)^(2) then k is equal to

Answer»

`1/(ALPHABETA)`
1
`-1`
`alpha beta`

ANSWER :B
Discussion
27924.

Find the area S of the ellipse given by the equation Ax^(2) + 2Bxy + Cy^(2) =1 (Delta = AC - B^(2) gt0, C gt 0)

Answer»


ANSWER :`(PI)/(sqrtDelta)`
Discussion
27925.

Prove that .(sin ((1)/(10))/((1)/(10)))gt ((sin ((1)/(9)))/((1)/(9))).

Answer»
Discussion
27926.

Using first principle, find the derivative of log_(e)x where x in (0,oo).

Answer»


ANSWER :`(1)/(X)`
Discussion
27927.

Cosider f(x)ax^(3)+bx^(2)+cx+d, where a,b,c,dinRanda!=0. If the equation f(x)=0 has three real roots alpha,beta,gamma such that alphaltbetaltgamma andL=Lim(|ax^(3)+bx^(2)+cx+d|)/(ax^(3)+bx^(2)+cx+d), where m in R, then which of the following may be correct ?

Answer»

`L=1ifbetaltmltgamma`
`L=-1ifalphaltmltbeta`
`L=-1ifbetaltmltgamma`
L=does not exist, if `m=beta`

SOLUTION :
`{:("when "betaltmltgamma_(,),"when "alphaltmltbeta,or""betaltmltgamma,),( :.F(x)gt0,f(x)lt0,:.f(x)lt0,),( :.L=1, :.L=-1,:.L=-1,):}`
When m `=beta,"the" underset(xtobeta)LIM(|ax^(3)+BX^(2)+cx+d|)/(ax^(3)+bx^(2)+cx+d)=` does not exist
As L.H.L. and R.H.L. will differ by NEGATIVE sign.
Discussion
27928.

The sinusoidal wave y(x,t) = ym sin(kx-omegat) is incident on the fixed end of a string at x = L. The reflected wave is given by :-

Answer»

`y_(m)SIN(kx+omegat)`
`-y_(m)sin(kx+omegat)`
`y_(m)sin(kx+omegat-kL)`
`y_(m)sin(kx+omegat-2kL)`

ANSWER :D
Discussion
27929.

int_(-pi/6)^(pi/6)sin^5xdx

Answer»

Solution :Let `F(x)=sin^5x`
Then`f(-x)=sin^5(-x)`
=`-sin^5x=-f(x)`
So f(x) is an odd FUNCTION.
Thus `int_-a^af(x)dx=0`
`therefore int_(-pi/6)^(pi/6) sin^5xdx=0`
Discussion
27930.

Solve graphically x + 2y - 5 le 0

Answer»

SOLUTION :
Discussion
27931.

Prove that every rational function is continuous.

Answer»


ANSWER :F is CONTINUOUS by (4) of Theorem 1.
Discussion
27932.

Evaluate the following integrals int2^(x)cosxdx

Answer»


ANSWER :`(2^(x))/((LOG2)^(2)+1)[log2.cosx+sinx]+C`
Discussion
27933.

Evalute the following integrals intsin ^(7) x dx

Answer»


ANSWER :`(4)/(3) e^(3X) + x + c`
Discussion
27934.

Let f : R to R be defined as f (x) =10 x +7. Find the function g : R to R such that g o f =f 0 g= 1 _(R).

Answer»


ANSWER :`G (y) = (y-7)/(10)`
Discussion
27935.

If A+B +C = 270^@, then cos 2A + cos 2B +cos 2C +4sin A sin B sin C=

Answer»

0
1
2
3

Answer :B
Discussion
27936.

A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.

Answer»


ANSWER :`3/8`
Discussion
27937.

If the quadratic equation 4x^(2) -2(a+c-1)x + ac-b (a gt b gt c) then:

Answer»

Both roots are greater than a
Both roots are less than c
Both roots are lie in `(c/2, b/2)`
Exactly one root lie in `(c/2, a/2)`

Solution :`4x^(2)- 2ax - 2cx + 2X + ac -b=0`
`2x(2x-a) -c(2x -a) + 2x-b=0`
`f(x) = (2x-a)(2x-c) + (2x-b)=0`
`f(a/2) = a-bf(c/2)=c-b`
`f(a/2)f(c/2)=(a-b)(c-b) lt 0`
`therefore (a GT b gt c)`
So exactly one root lie in `(c/2, a/2)`
Discussion
27938.

If vecaxx(vecbxxvecc)=(vecaxxvecb)xxveccfor non coplanar veca,vecb,vecc then……

Answer»

`veca` parallel to `vecb`
`vecb` parallel to `VECC`
`vecc` parallel to `veca`
`veca+vecb+vecc=vec0`

ANSWER :C
Discussion
27939.

Let a,b and C be three non - coplanar vectors and let p,q and r be the vectors defined by p = (b xx c)/([a b c]). Q = (c xx a)/([a b c]). R (a xx b)/([a b c ]). Then (a + b). P + (b + c) q + (C + a) . R =

Answer»

0
1
2
3

Answer :D
Discussion
27940.

Find the equation of image circle of the circle x^(2)+y^(2)-2x=0 in the line x+y-2=0

Answer»


ANSWER :1
Discussion
27941.

There are fifteen players for a cricket match In how many ways the 11 players can be selected excluding two particular players?

Answer»


ANSWER :78
Discussion
27942.

Ifxissmall, so thatx ^ 2andhigherpowerscan beneglected,thentheapproximatevalue for((1- 2x ) ^( -1)(1- 3x ) ^( -2)) /((1 - 4 x) ^( -3))

Answer»

`1 - 2x`
` 1 - 3X `
`1 -4x `
` 1 -5 x `

SOLUTION :`((1- 2x ) ^(-1) (1 - 3x )^(-2)) / ((1-4x ) ^(-3)) `
`=(1 -2x ) ^(-1) ( 1 - 3x ) ^(-2)( 1 - 4x ) ^3 `
`=(1+2x+4x ^ 2+… )( 1 +6x+…)( 1 - 12 x ) `
`= (1+ 8X )( 1 - 12 x ) `
`= 1 -4 x `
Discussion
27943.

Write the range of f(x)=sin^(-1) x" in "[0,2pi] other than [-pi/2,pi/2]

Answer»


ANSWER :`[-(3PI)/2,(-PI)/2] or [pi/2,(3pi)/2]`
Discussion
27944.

If bar(a),bar(b),bar( c ) are mutually perpendicular vectors having magnitudes 1, 2, 3 respecively then [bar(a)+bar(b)+bar( c )""bar(b)-bar(a)""bar( c )]=

Answer»

0
6
12
18

Answer :C
Discussion
27945.

Express A= [{:(3,5),(1,-1):}] as sum of symmetric and skew symmetric matrix.

Answer»


ANSWER :`(1)/( 2)( A+ A^(1) ) + (1)/(2)A-A^(1) = A`
Discussion
27946.

Match the following

Answer»


ANSWER :A
Discussion
27947.

Identify the quantifier in the following statements and write the negation of the statement.(ii)For every real number x,x is less than x+1.

Answer»

SOLUTION :For EVERY
Discussion
27948.

The product of the lengths of perpendiculars drawn from any point on the hyperbola x^(2)-2y^(2)-2=0 to its asymptotes is

Answer»

`1/2`
`2/3`
`3/2`
2

Answer :B
Discussion
27949.

The nearest point on the circle x^(2)+y^(2)-6x+4y-12=0 from (-5,4) is

Answer»

(1,1)
(-1,1)
(-1,2)
(-2,2)

ANSWER :B
Discussion
27950.

int [ sin(log x)+ cos (log x ) ] dx =

Answer»

x COS (log x) + c
`-`x cos(log x) + c
x log (sinx ) + c
x SIN (log x) + c

ANSWER :D
Discussion