InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 27851. |
Find the number of ways of arranging 6 red roses and 3 yellow roses of different sizes into a garland. In how many of them no two yellow roses are together |
|
Answer» <P> |
|
| 27853. |
A person has undertaken a construction job. The probablities are 0.65 that will be strike, 0.80 that the constructionjob will becompleted on timeif there is no strike, and 0.32 thatthe construction job will be completed on time if there is a strike. Then the probability that the construction job will be completed on time is |
|
Answer» `0 . 788` |
|
| 27854. |
Two matrices are equalif they have same number of rows and same number of columns . |
|
Answer» |
|
| 27855. |
Out of 800 boys in a school , 224 played cricket,240 played hookey and 336 played basketball. Of the total , 64 played both basketball and hockey , 80 played cricket and basket ball and 40 played cricket and hockey 24 played all the three games. number of boys who did not play any game is |
|
Answer» 160 |
|
| 27856. |
Ifalpha, beta , gammaare therootsof x^3+2x^2 -3x -1=0 thenalpha^(-2)+ beta^(-2)+ gamma^(-2)= |
|
Answer» 12 |
|
| 27857. |
Write the vector form of the equation of the line (x-3)/3=(y+4)/7=(z-6)/2 |
|
Answer» |
|
| 27858. |
If |z_(1) + z_(2)| = |z_(1) - z_(2)| then the difference in the arguments of z_(1) and z_(2) is |
|
Answer» `(PI)/(4)` |
|
| 27859. |
Find the rate of change of the area of a circle with respect to its radius r when (a) r=3 cm "" (b) r=4 cm |
|
Answer» |
|
| 27860. |
Let p, q be prime numbers such that non n^(3pq)-nis a multiple of 3pq for all positive integers n. Find the least possible value of p + q. |
|
Answer» |
|
| 27861. |
Choose the correct answer If d/(dx)f(x)=4x^(3)-3/(x^(4)) such that f (2) = 0. Then f (x) is |
|
Answer» `X^(4)+1/(x^(3))-129/8` |
|
| 27862. |
Let A(theta) and B(phi) be the extrenities of a chord of an emplise. If the slope of AB is equal to the slope of the tangent at a point C(alpha) on the ellipse, then value of alpha is |
|
Answer» `(theta+phi)/2` |
|
| 27863. |
The normal ata point P on the parabola y^(2)=4axcuts the curve again at Q . If M is the midpoint of PQ then the product of the ordinates of P and M is |
|
Answer» `a^(2)` |
|
| 27864. |
Let f be a continuous function satisfying f(x+y)=f(x)+f(y) for all x,y in R and f(1)=5 then lim_(x to 4) f(x) is equal to |
|
Answer» 4 |
|
| 27865. |
Prove that following i) 2.C_(0)+5.C_(1)+8.C_(2)+…..+(3n+2)C_(n)=(3n+4).2^(n-1) |
|
Answer» `(4 -3N).2^(2n-1)` |
|
| 27866. |
Pick out a function which is one - one but not onto |
|
Answer» Let `A={a,B,C},B={2,4}`. Define |
|
| 27867. |
Let R = {(a,a^3) | ais a prime number less than 10}.Find dom R^(-1). |
| Answer» Solution :R = {(a,a^3)| a is a prime number LESS than 10. DOM R^(-1) = {8,27,125,343) RNG R | |
| 27868. |
Find the point at which the tangent to the curve y=sqrt(4x-3)-1 has its slope (2)/(3). |
|
Answer» |
|
| 27869. |
At present, a firm is manufacturing 2000 items. It is estimated that the rate of change of production P w.r.t additional number of workers x is given by (dP)/(dx) = 100 - 12 sqrtx. If the firm employs 25 more workers, then the new level of production of items is |
|
Answer» 3500 |
|
| 27870. |
Let p,q, r denote respectively the statements :" you are honest ", "you are laborious ","you will receive a promotion" Translate p^^q^^rstatements into English language. |
| Answer» SOLUTION :You are HONEST and LABORIOUS and you will RECEIVE a PROMOTION. | |
| 27871. |
I:(1)/(1!)+(1+2)/(2!)+(1+2+2^(2))/(3!)+....=e^(2)-e II:(2)/(2!)+(2+4)/(3!)+(2+4+6)/(4!)+....=e |
|
Answer» only I is TRUE |
|
| 27872. |
A die is thrown three times. Events A and B are defined as below: A : 4 on the third throw B : 6 on the first and 5 on the second throw Find the probability of A given that B has already occurred. |
|
Answer» |
|
| 27873. |
consider the function f(x) =1+(1)/(x)^(x) The range of the function f(x) is |
|
Answer» `(0,poo)` f(x) is defined if`1+1/xgt0 or (x+1)/(x)gt0` or `(-oo,-1)cup(0,oo)` Now f(X)=`(1+(1)/(x))^(x)ln (1+(1)/(x))+(x)/(1+(1)/(x))(-1)/(x^(2))` `=(1+(1)/(x))^(x)ln(1+(1)/(x))-(1)/(x+1)` Now `(1+(1)/(x))^(x)` is always positive Hence the sign of f(X) Depends on the sign of ln `(1+(1)/(x))-(1)/(1+x)` Let `g(x)=In (1+(1)/(x))-(1)/(x+1)` `g(x)=(1)/(1+(1))(x)(-1)/(x^(2))+(1)/(x+1)^(2)=(-1)/(x(x+1)^(2)` (i)for `x in (0,oo)g(x)lt0` Thus g(X) is monotonically decreasing for x in `(0,oo)` or `g(X) gt underset(xrarroo)limg(x)` or `g(X)gt0, so f(X) gt0` (ii)for `x in (-oo,-1),g(x)gt0` Thus g(X) is monotonically INCREASING for `x in (-oo,-1)` or `g(X) gt underset(xrarroo)limg(X)gt0` `THEREFORE f(x)gt0` Hence FORM (i) nd (ii) we get `f(X) gt0 FORALL x in (-oo,-1)cup(0,oo)` Thus f(x) is montonically increasing in its domain Also `underset(xrarroo)lim(1+(1)/(x))^(x)`=e `underset(xrarr0)lim(1+(1)/(x))^(x)=1 and underset(xrarr-1)lim(1+(1)/(x))^(x)=oo` The graph of f(X) is shown in figure  Range is `y in (1,oo)-{e}` |
|
| 27874. |
Differentiate the following with respect to x: cos^(-1) (e^(x)) |
|
Answer» |
|
| 27875. |
int_0^(pi//2)(sqrttanx+sqrtcotx)dx |
|
Answer» SOLUTION :`int_0^(pi/2)(sqrttanx+sqrtcotx)DX` =`int_0^(pi/2)(sinx+cosx)/sqrt(sinxcosx)dx` =`sqrt2int_0^(pi/2)(sinx+cosx)/sqrt(1-(sinx-cosx)^2)dx` =`SQRT2[sin^-1(sinx-cosx)]_0^(pi/2)` =`sqrt2(sin^-1 1-sin^-1(-1))` =`sqrt2(pi/2+pi/2)=sqrt2pi` |
|
| 27876. |
Which of the following is not a requirement of binomial distribution? |
|
Answer» There are TWO outcomes for each trial |
|
| 27877. |
If int(2e^(5x)+e^(4x)-4e^(3x)+2e^(x))/((e^(2x)+4)(e^(2x)-1)^(2))dx=tan^(-1)(e^(x//2))-(K)/((e^(2x-1)))+C then K is equalto |
|
Answer» |
|
| 27878. |
int_(-1)^(1) (17x^(5)-x^(4)+29 x^(3) -31 x +1)/(x^(2)+1)dx= |
|
Answer» `4/5` |
|
| 27879. |
If a_1,a_2,a_3….a_r are in G.P then show that |{:(a_(r+1),a_(r+5),a_(r+9)),(a_(r+7),a_(r+11),a_(r+15)),(a_(r+11),a_(r+7),a_(r+21)):}| is independent of r |
|
Answer» |
|
| 27880. |
Probability distribution of random variable X is as follows: WhereC gt 0 Find (i) C (ii) P(X lt 2) (iii) P(1 lt X le 2). |
|
Answer» |
|
| 27881. |
Draw the graph of y = tan^(2) x. |
|
Answer» Solution :We have `y = f(x) = tan^(2) x` Period of the function is `pi`. Function is EVEN, so the graph is symmetrical above the x - axis. Let us DRAW the graph for `0 lt x lt pi//2`. For `0 lt x lt pi//4, 0 lt tan x lt 1` `therefore` `tan^(2) x lt tan x` For `x gt pi//4` `tan x gt 1` `therefore` `tan^(2) x gt tan x` Hence the graph of `y = tan^(2) x` lies below and above the graph of y = tan x for `x in (0, pi//4)` and `x in (pi//4, pi//2)`. So the graph of the function for `x in (-pi//2, pi//2)` is as SHOWN in the FOLLOWING figure. 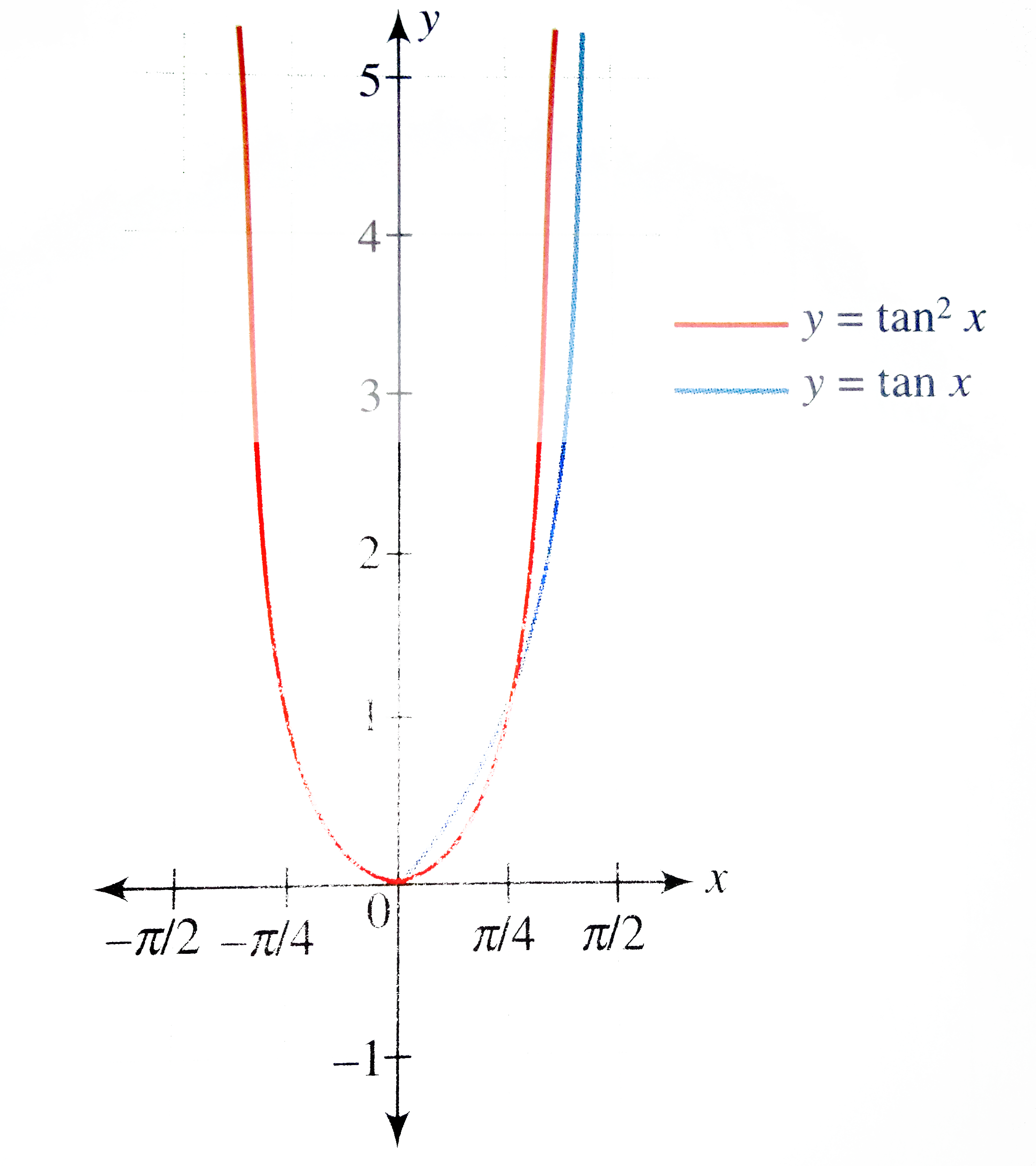 Since the function has period `pi` , the graph of the function is as shown in the following figure. 
|
|
| 27883. |
If a variable takes the values 0, 1, 2,…,n with frequencies proporiotnal to binomial coefficient n_(C_(0)), n_(C_(1)), n_(C_(2)),….n_(C_(n)), then mean of distribution is |
| Answer» Answer :C | |
| 27884. |
Mean of the following probability distribution is ………… |
|
Answer» `(7)/(8)` |
|
| 27885. |
If X is a poisson variate such that P(X = 2) = 9P(X = 4) + 90P(X = 6) then find mean of X. |
|
Answer» |
|
| 27886. |
The period T and length l are increasing at the same rate is T = 2pi sqrt(l//g). Then the length l in terms of pi and g is |
|
Answer» `PI//G` |
|
| 27887. |
If vec(a), vec(b), vec(c) are the position vectors of vertices A, B, C of a triangle ABC, Show that the area of the triangle is (1)/(2) |vec(b) xx vec(c) + vec(c) xx vec(a) + vec(a) xx vec(b)| |
|
Answer» |
|
| 27888. |
Find the points on the curve x^(2)+y^(2)-2x-3=0 at which the tangents are parallel to the X-axis. |
|
Answer» `(0, pm SQRT(3))` |
|
| 27889. |
Each of the following defines a relation of N : x+y = 10 , x , y in N Determine which of the above relations are reflexive , symmetric and transitive . |
|
Answer» |
|
| 27890. |
In howmanywayscan 52cardsbe dividedamong4playersso thateach mayhave 13is |
|
Answer» `(52!)/(13!^(4))` |
|
| 27891. |
If a=hat(i)-2hat(j)+hat(k), b=hat(i)+3hat(j)-2hat(k), c=2hat(i)+hat(j)-hat(k) " and "d=hat(i)+hat(j)+hat(k), then the volume (in cubic units) of the tetrahedron having (a times b) times c, b, d as its coterminuous edges is |
|
Answer» `15/2` |
|
| 27892. |
cos (alpha + beta + gamma ) + cos (alpha - beta - gamma) + cos ( beta - gamma- alpha ) + cos ( gamma - alpha - beta )= |
|
Answer» `2cos ALPHA cos beta cos GAMMA` |
|
| 27893. |
A, B, C are the centres of three circles of equal radii which donot touch extranally pairwise whose centers are non-collinear. The radical centre of the circles for triangle ABC is |
|
Answer» circumcentre |
|
| 27895. |
find the order and degree of the differential equation: |
|
Answer» |
|
| 27896. |
Integrate the following : int(sqrtx+2)^2/x^4dx |
|
Answer» SOLUTION :`INT(sqrtx+2)^2/(x^4)DX` =`int(x+4+2xx(2sqrtx))/(x^4)dx` =`int(x^-3+4x^-4+4x^(-7/2))dx` =`x^-2/-2+4(x^-3)/-3+4x^(-5/2)/(-5/2)+C` =`-1/2xx1/(x^2)-4/3xx1/(x^3)-8/5xx1/x^(5/2)+C` |
|
| 27897. |
Obtain the following integrals : int(2x-1)/(2x+3)dx |
|
Answer» |
|
| 27898. |
Discuss the continuity of the function f, where f is defined by f(x)={{:(3," if "0 le xle 1),(4," if "1 lt x lt 3),(5," if "3 le x le 10):}. |
|
Answer» |
|
| 27899. |
If the vectors a=hat(i)+a hat(j)+a^(2) hat(k), b=hat(i)+b hat(j)+b^(2) hat(k) and c=hat(i)+chat(j)+c^(2) hat(k) are three non-coplanar vectors and |(a,a^(2),1+a^(3)),(b,b^(2),1+b^(3)),(c,c^(2),1+c^(3))|=0, then the value of abc is |
|
Answer» 0 `RARR""Delta=|{:(1,a,a^2),(1,b,b^2),(1,c,c^2):}|ne0rArrDeltane0` `"Now,"|{:(1,a^2,1+a^3),(1,b,1+b^3),(1,c^2,1+c^3):}|=0` `rArr""|{:(1,a^2,1),(1,b,1),(1,c^2,1):}|+|{:(a,a^2,a^3),(b,b^2, b^3),(c,c^2,c^3):}|=0` `rArr""Delta(1+abc)=0rArr""abc=-1[because Delta=ne]` |
|
| 27900. |
If ax ^2 + 2bx+ c=0 , a_1x^2+ 2b _1x +c_1=0havea commonroot, thenthe rootsof theequation( b^2 -ac )x^2+(2b b_1 - a a_1 - a_1 c ) x+ (b_1^2-a_1 c_1 ) =0 are |
| Answer» Answer :B | |