InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3151. |
Match the following: |
|
Answer» `{:("P","Q","R","S"),("2","1","4","3"):}` |
|
| 3152. |
Obtain the following integrals : int(1)/(sqrt(16-9x^(2)))dx |
|
Answer» |
|
| 3153. |
Common roots of the equations z^(3)+2z^(2)+2z+1=0 and z^(1985)+z^(100)+1=0 are |
|
Answer» `OMEGA,omega^(2)` |
|
| 3154. |
If A is square matrix of order 2xx2 such that A^(2)=I,B=[{:(1,sqrt(2)),(0,1):}] and C=ABA then |
|
Answer» `C^(2009)=A[{:(1,2009sqrt(2)),(0,1):}]` continuing in the MANNER `C^(2008)=AB^(2009)A` `B^(2)=[{:(1,2sqrt(2)),(0,1):}],B^(3)=[{:(1,3sqrt(2)),(0,1):}]` Continuing in this manner `B^(2009)=[{:(1,2009sqrt(2)),(0,1):}]` |
|
| 3155. |
{:("Column A","", "Column B"),("The area of square with perimeter 12",,"The area of a parallelogram with perimeter 16"):} |
|
Answer» If column A is larger |
|
| 3156. |
I) The maximum value of c + 2bx -x^(2) is c+b^(2) II) The minimum value of x^(2) + 2bx + c is c-b^(2) Which of the above statements is true ? |
|
Answer» ONLYI is true |
|
| 3157. |
If int(cos^(3)xdz)/((sin^(4)+x+3sin^(2)x+1)tan^(-1)(sinx+cosec x))=-Alog |tan^(-1)(sinx+cosecx)|+C then A is equal to. |
|
Answer» |
|
| 3159. |
Form the differential equation of the family of circles having centre on y-axis and radius 5 units. |
|
Answer» |
|
| 3160. |
A cubic polynomial P is such that P(1) = 1, P(2) = 2, P(3) = 3 and P(4) = 5. Then P(6) is |
|
Answer» |
|
| 3161. |
State which of the following matrices is symmetric,slew symmetric, both or not either: [[0,1,2],[-1,0,3],[-2,-3,0]] |
| Answer» SOLUTION :SKEW SYMMETRIC | |
| 3162. |
If (1+x+2x^(2)+4x^(3))^(10)=a_(0)+a_(1)x+a_(2)x^(2)+….+a_(30)x^(30). Find the value of a_(0)-a_(1)+a_(2)-a_(3)…+a_(30) |
|
Answer» |
|
| 3163. |
Differentiate sqrt(tanx |
|
Answer» SOLUTION :LET `y=sqrt(TANX)=(tanx)^(1/2)` Then `dy/dx=1/2(tanx)^(1/2)xxd/dx(tanx)` `=1/(2sqrt(tanx))CDOT sec^2x` |
|
| 3164. |
Two events A and B are such that P(B) = 0 . 55and P(AB') = 0 . 15 . Theprobability of occurenceof at least one of eventis |
|
Answer» `0.70` |
|
| 3165. |
IFalpha, betaare therootsof theequationax^2 + bx +c=0 andalphalt -1,beta gt 1 then1 +(c )/(a)+ |(b)/(a)| is |
|
Answer» positive |
|
| 3166. |
Let f(x) = (x + x^(2) + ...+ x^(n)-n)/(x -1), x ne 1, the value of f (1) |
|
Answer» N |
|
| 3167. |
At a party, each man danced with exactly four women and each woman danced with exactly three men. Nine men attended the party. How many women attended the party? |
|
Answer» |
|
| 3168. |
Which of following functions have the same graph? |
|
Answer» `f(x)=log_(E)e^(x)` |
|
| 3169. |
Find the number of 4-digit number that can be formed using the digits 1,2,3,4,5,6 that are divisble by when repectiton is allowed |
|
Answer» |
|
| 3170. |
If A and B are conjugate points w.r.t to circle x^(2)+y^(2)=r^(2) then OA^(2)+OB^(2)= |
|
Answer» `AB^(2)-r^(2)` |
|
| 3171. |
Evaluate int_(0)^((1)/(sqrt(2)))(x^(3))/(sqrt(1-x^(2))) dx |
|
Answer» |
|
| 3172. |
The tangent at any point P of a curve C meeta the x-axis at Q whose abscissa is positive and OP = OQ where O is origin, if C is a family of parabola having vertex (alpha, beta) and latus- rectum = 4a, then find value of (4(alpha+beta))/a ? |
|
Answer» |
|
| 3173. |
If the system of linear equations ax+by+cz=0 cx+ay+bz=0 bx+cy+az=0 where a,b,c in R are non-zero and distinct , has a non-zero solution, then : |
|
Answer» a+B+C=0 `RARR (a^2-bc)-b(ac-b^2)+c(c^2-ab)=0 rArr a^3 -abc-abc+b^3+c^3-abc=0` `rArr a^3+b^3+c^3-3abc=0 rArr (a+b+c)(a^2+b^2+c^2-ab-b-ca)=0` `rArr` a+b+c=0 |
|
| 3174. |
Solve the following in equations : i) sqrt(x+2) gt sqrt(8-x^(2)) ii) sqrt((x-3)(2-x)) lt sqrt(4x^(2)+12x+11) iii) sqrt(x^(2)-3x-10) gt 8-x |
|
Answer» |
|
| 3175. |
Let f(x)= x^(3)-x^(2) + x + 1 g(x) = max I {f(t), 0 le t le x}, 0 le x le 1= 3-x, 1 lt x le 2 Then in [0, 2] the points where g(x) is not differentiable is……… |
|
Answer» 0 |
|
| 3176. |
If sqrt(9x^(2)+6x+1) lt 2-x, then |
|
Answer» ` X in ((-3)/(2), 1/4)` |
|
| 3178. |
Find the number of possible common tangents that exist for the following pairs of circles. x^(2) + y^(2) = 4, x^(2) + y^(2) - 6 x - 8y + 16 = 0 |
|
Answer» |
|
| 3179. |
The value of Lim_(xto0) (5x^(2)+[x^(2)+1])^(((1)/(x^(2)+sin^(2)x))) is, [Note : [y] denotes greatest interger less than or equal to y.] |
|
Answer» `(5)/(2)` where `L=underset(xto0)Lim(1)/(x^(2)+sin^(2)x)(5x^(2)+[x^(2)+1]-1)=underset(xto0)Lim(5x^(2))/(x^(2)+sin^(2)x)=(5)/(2)` `:."Limit"=e^((5)/(2))`. |
|
| 3180. |
Three poles whose feet lie on a circle subtend angle alpha, beta, gamma respectively at the centre of the circle. If the height of the poles are in A.P. then cot alpha, cot beta, cot gamma are in |
|
Answer» A.P. |
|
| 3181. |
If p is any statement, then (^^~p) is a |
|
Answer» contingency |
|
| 3182. |
If p is any statement, then (p^^~) is a |
|
Answer» contingency |
|
| 3183. |
If y = mx + c is a normal to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 if C= |
|
Answer» `(a^(2)-B^(2))/(a^(2)m^(2)+b^(2))` |
|
| 3184. |
A = {1,2,3,4} , B = {1,5,9,11,15,16} f = {(1,5),(2,9),(3,1),(4,5),(2,11)} Is f a relation from A to B ? Give reason for your answer. |
|
Answer» |
|
| 3185. |
An electric bulb will last 190 days or more with a probability 0.7 and it will last for atmost 200 days with a probability of 0.8. The probability that the bulb will last between 190 and 200 days is |
|
Answer» `0.5` |
|
| 3186. |
Consider the circlex^(2)+y^(2)_4x-2y+c=0 whose centre is A(2,1). If the point P(10,7) is such that the line segment PA meets the circle in Q with PQ=5 then c= |
|
Answer» `-15` |
|
| 3187. |
The set of allpointswhere f(x) = root(3)(x^(2)|x|)-|x|-1 is notdifferentiableis |
| Answer» Answer :D | |
| 3188. |
int (dx)/((x+2)(x^(2)+1))=a log|1+x^(2)|+btan^(-1)x+(1)/(5)log|x+2|+C then ... Of the following is true. a) a=-(1)/(10), b=-(2)/(5)b) a=(1)/(10), b=-(2)/(5)c) a=-(1)/(10), b=(2)/(5)d) a=(1)/(10), b=(2)/(5) |
|
Answer» `a=-(1)/(10), b=-(2)/(5)` |
|
| 3189. |
Consider the parabola whose focus is at (0,0) and tangent at vertex is x-y+1=0 Tangents drawn to the parabola at the extremities of the chord 3x+2y=0 intersect at angle |
|
Answer» `pi//6`  The distance between the focus and tangent at the vertex is `(|0-0+1|)/(sqrt(1^(2)+1^(2)))=(1)/(sqrt(2))` The directrix is the line parallel to the tangent vertex ant at a distance `2xx1sqrt(2)` from the focus. Let the EQUATION of the directrix be `x-y+lamda=0` where `(lamda)/(sqrt(1^(2)+1^(2)))=(2)/(sqrt(2))` `:." "lamda=2` Let P (x,y) be any moving point on the parabola. Then, OP=PM `orx^(2)+y^(2)=((x-y+2)/(sqrt(1^(2)+1)))^(2)` `or2x^(2)+=2y^(2)=(x-y+2)^(2)` `orx^(2)+y^(2)+2xy-4x+4y-4=0` Latus rectum length `=2xx` (Distance of focus from directrix) `2|(0-0+2)/(sqrt(1^(2)+1^(2)))|=2sqrt(2)` Solving the parabola with the x-axis, we get `x^(2)-4x-4=0` `orx=(4pmsqrt(32))/(2)=2pm2sqrt(2)` THEREFORE, the length of chord on the x-axis is `4sqrt(2)`. Since the chord 3x+2y=0 PASSES through the focus, it is focus chord. Hence, tangents at the EXTREMITIES of chord are perpendicular. |
|
| 3190. |
The polars of any two points A and B wrt a circle, centre O meet at P. Then AP^(2)-BP^(2)= |
|
Answer» `AO^(2)+BO^(2)` |
|
| 3191. |
Statement-1 :The weighted mean of first n natural numbers whose weights are equal is given by ((n+1)/2) . Statement-2 : If omega_1,omega_2,omega_3, … omega_n be the weights assigned to be n values x_1,x_2,… x_n respectively of a variable x, then weighted A.M. is equal to (Sigma_(i=1)^(n) omega_ix_i)/(Sigma_(i=1)^(n) omega_i) |
|
Answer» |
|
| 3192. |
A manufacture produces two models of bike model X and model Y. Model X takes a 6 man hours to make per unit, while model Y takes 10 man hours per unit. There is a total of 450 man hour availbale per week. Handling and marketing costs are 2000 and 1000 per unit of model X and Y, respectively. The tota funds available for these purposes are 8000 per week. Profits per unit for models X and Y are 1000 and manufacturer produce, so, as to yeild a maximum profit? Find the maximum profit. |
|
Answer» `therefore 6x+10y le 450` `Rightarrow3x+5y le 225....(i) ` For models X and Y, handling and marketing costs are 2000 and 1000 respectively, total FUNDS available for these purposes are 80000 per week. `therefore 2000x+1000y ge 80000` `Rightarrow 2x+y ge 80` Also, `x ge 0, y ge....(ii)` Hence the profits per unit fo r models X and Y are 1000 and 500 respectively`therefore "Required LPP i"` Maximise Z=1000x+500y Subject to `3x+5y le 225, 2x+y le 80, x ge 0, y ge 0` From the shaded feasible region, it is clear that COORDINATES of corner points are (0,) (40,0),(25,30) and (0,45) On solving 3x+5y=225 and 2x+y=80, we get x=25, y=30 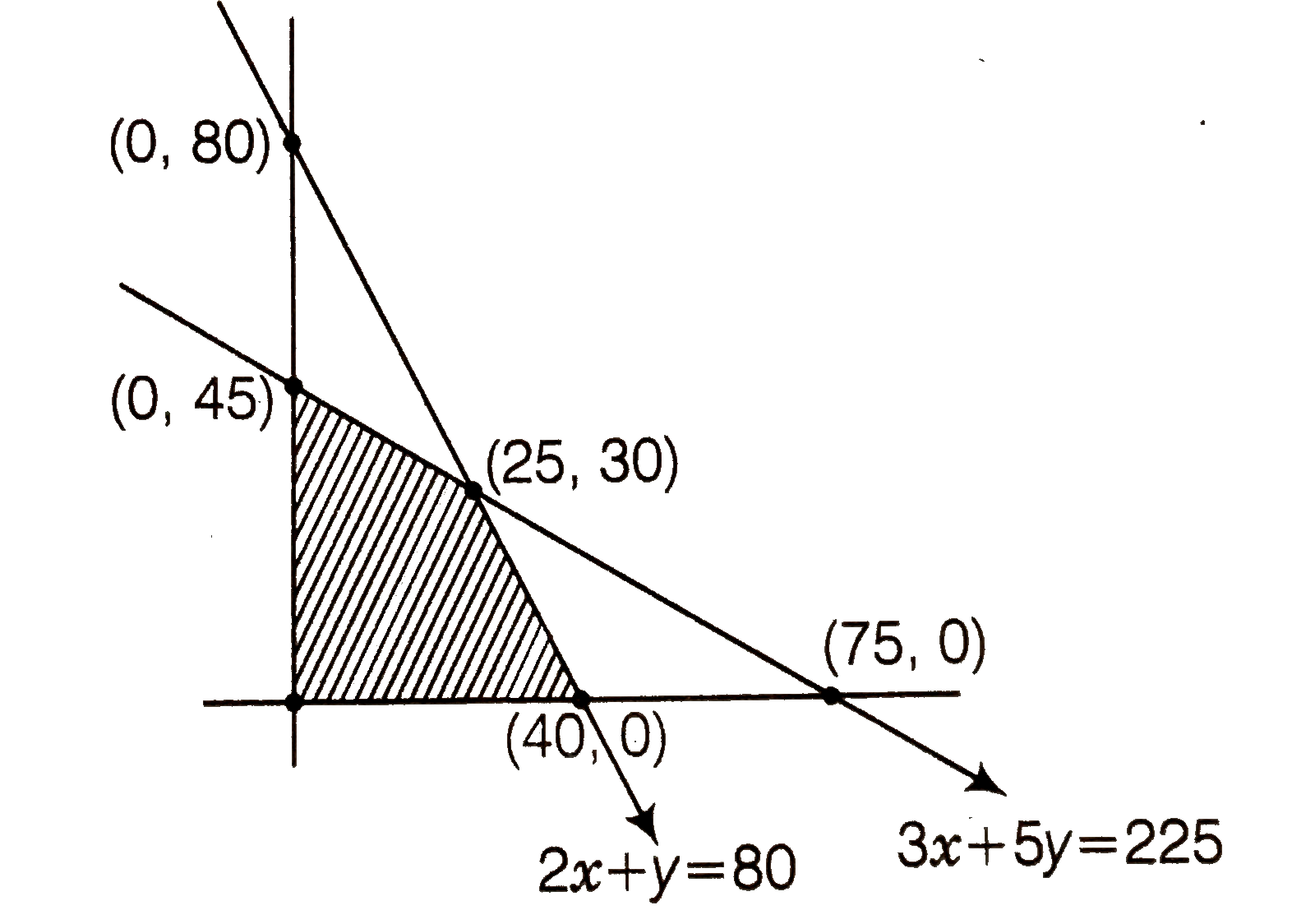 So, the manufacturer should poroduce 25 bikes of model X and 30 bikes of model Y to get a maximum PROFIT of 40000. Since in question it is asked that each model bikes should be produced. |
|
| 3193. |
Where line XY is parallel to line QU. If b=4x, e=x+2y and d=3y+8, find h. |
|
Answer» |
|
| 3194. |
Find the direction cosines of perpendicular from the origin to the plane vecr.(6hati-3hatj-2hatk)+1=0. |
|
Answer» |
|
| 3195. |
Distance between parallel lines r=2i+lambda(i+j+k) and r=-3j+mu(i+j+k) is |
|
Answer» `SQRT((14)/(3))` |
|
| 3196. |
Let f be a function defined on R by f(x)=lim_(n to oo) (log (3+x)-x^(2n) sinx)/(1+x^(2n)) then |
|
Answer» F is CONTINUOUS on R |
|
| 3197. |
Assertion (A) : If alpha is a root of x^5=1 then the value of(1-alpha)(1-alpha^2)(1-alpha^3)(1-alpha^4)=5Reason (R) : If omega is n^(th) roots od unity then the values of (1-omega)(1-omega^2)(1-omega^3)…...(1-omega^(n-1))=n |
|
Answer» Both A and R are TRUE R is CORRECT explanation to A |
|
| 3198. |
Let a_(n)=i^((n+1)^2), where i=sqrt(-1)" and "n=1, 2, 3,"………..". Then the value of a_(1)+a_(3)+a_(5)+"……….."+a_(25) is |
| Answer» ANSWER :A | |
| 3199. |
Show that the function f(x)=x^(3)+1/(x^(3)) is decreasing function in the interval [-1,1]-{0}. |
| Answer» | |
| 3200. |
"The maximum or the minimum of the objective function occurs only at the corner points of the feasible region". This theorem is know as fundamental theorem of |
|
Answer» Agebra |
|