InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3251. |
Digestive system includes :- |
|
Answer» ALIMENTARY canal only |
|
| 3252. |
if [(cos""(2pi)/(3),-sin""(2pi)/(3)),(sin""(2pi)/(3),cos""(2pi)/(3))]^(k)=[(1,0),(0,1)] Then the least value of k equals (kne0) |
|
Answer» 1 |
|
| 3253. |
Let L be the line parallel to the vectors sqrt(2) hati - 5 hatj + 3 hatkand passing through the point a given by hati + 2 hatj - 3 hatk . If the distance between A and a point P on the line L is 18 units , then the position vector of such a point P is |
|
Answer» `(1- 3 SQRT2) hati + 17 HATJ- 12 hatk` |
|
| 3254. |
The maximum possible area bounded by the parabola y= x^(2)+x+10 and a chord of the parabola of length 1 is |
| Answer» ANSWER :B | |
| 3255. |
If x = 2.352, then x equals: |
|
Answer» `(2352)/(999)` |
|
| 3256. |
Consider the random experiment of tossing three coins. If X denote, the number of tails in the sample space, exhibit X. |
|
Answer» SOLUTION :X(HHH)=0, X(HHT)=1, X(HTH)=1, X(THH)=1, X(THT)=2, X(TTH)=2, X(HTT)=2, X(TTT)=3 RANGLE of X is {0, 1, 2, 3} |
|
| 3257. |
The probability that a student is not a swimmer is 1/5 then the probabilitythat out of five student , four are swimmer is |
|
Answer» `"^5C_4(4/5)^4 (1/5)` |
|
| 3258. |
If [cot^(-1)x]+[cos^(-1)x]=0 then complete set of values of 'x' is (where [*] denotes the greatest integer function) |
| Answer» Answer :C | |
| 3259. |
Let S be the sample space of all 3xx3 matrices with entries from the set {0,1} . Let the events E_1 and E_2 be given by E_1={A in S: det A=0} and E_2={A in S : "Sum of entries of" A is 7} if a matrix is chosen at random from S, then the conditional probability P(E_1|E_2) equals........... |
|
Answer» `E_1={A in S :det(A)=0}` and `E_2={A in S: "Sum of entries of" A is 7}`. For event `F_2`. Means sum of entries of matrix A is 7, then we need SEVEN 1s and two 0s. `therefore` Number of different possible matrices `=(91)/(7! 2!)rArr n(E_2)=36` For event `E_1,|A|=0`, both the zeroes must be in same row/column. `therefore` Number of matrices such that their determinant is zero. ` 6xx (3!)/(2!)=18=n(E_1 cap E_2)` `therefore` Requried probability, `P(E_1)/(E_2)=(n(E_1cap E_2))/(n(E_2))` ` = (18)/(36) =(1)/(2)=0.50`. |
|
| 3260. |
A balanced coin is tossed thrice. Then following events are defined. Event A = Head is obtained on first toss. Event B = Tail is obtained on last toss. Does A and B are independent ? |
|
Answer» |
|
| 3261. |
For a Binomial veriate X , if n = 4 and P(X = 4) = 6 P(X =2), then the value of p is |
|
Answer» `3/7` |
|
| 3262. |
If the two lines (x-1)/2 = (y+1)/3 = (z-1)/4and(x-3)/1 = (y+k)/2 = z/1 have a point in common, then k = |
|
Answer» `2/9` |
|
| 3263. |
Find the values of the following integrals (iii) int_(0)^(pi/2) cos^(11) x dx |
|
Answer» |
|
| 3264. |
""^(2n +1)C_0^2 -""^(2n+1)C_1^2 + ""^(2n+1)C_2^2 -…….- ""^(2n+1)C_(2n+1)^2 = |
|
Answer» 0 |
|
| 3265. |
The volume of solid obtained by revolving the curve y=sec x between x=(pi)/(4). |
|
Answer» `2PI(1-SQRT(3))` |
|
| 3267. |
Statement-I: The sine and cosine curves intersect infinitely many tmes, bounding regions of equal areas. Statement-II : The area of the figure bounded by the curves y=cos x and y=sin x and the ordinates x = 0 and x=(pi)/(4) is sqrt(2)-1 sq. units. Which of the above statement is correct. |
|
Answer» only I |
|
| 3268. |
One number is selected from the set S={1,2,3, …., 50} A={n in S//n +(50)/(n) gt 27} B={n in S//n " is prime number"} C={n in S//n " is perfect square"} Then ………of the following probability relation is valid |
|
Answer» `P(A) LT P(B) lt P(C )` |
|
| 3269. |
If alpha, beta ,gamma are roots of x^(3) + px + q = 0 then (alpha^(5) + beta^(5) + gamma^(5))/(5) = |
|
Answer» `(alpha^(3) + beta^(3) + gamma^(3))/(3) .(alpha^(2) + beta^(2) + gamma^(2))/(2)` |
|
| 3270. |
Number of even divisors of 1600 is |
|
Answer» 21 |
|
| 3271. |
A(-2, 2, 3) and B(13, -3, 13) and L is a line through A. Q. Equation of a line L, perpendicular to the line AB is |
|
Answer» `(x+2)/(15)=(y-2)/(-5)=(z-3)/(10)` |
|
| 3272. |
Match the following: |
|
Answer» <P>`{:(P,Q,R,S),(2,1,4,3):}` |
|
| 3273. |
The sidesofa trianglearesinalpha, cosalphaandsqrt( 1+ sinalphacos alpha ) for some 0 ltalphalt pi/2 thenthe greaterangleof thetriangleis |
| Answer» ANSWER :A | |
| 3274. |
I : A particle is projected vertically upward its heighth at time t is given by h=60t -16t^2. The velocity at which it hits the ground is 60 units /sec. II : A stone is thrown up vertically and the height h reached in time t given by h=80t -16t^2. The stone reaches the maximum height in 5/2 secs. |
|
Answer» only I is TRUE |
|
| 3275. |
Let f(x)={a^(2)+a+1}+bcosec^(-1)x where a epsilonI and b gt0. If range of f(x) is[p,r]uu(r,q], then the value of (p^(2))/(q^(2))+r^(2) equals |
|
Answer» `1` |
|
| 3276. |
Find the number of six digit number between 700000 and 800000 such that the first digit is equal to the sum of the other five digits. |
|
Answer» Solution :u+v+W+x+y=7, where u,v,w,x,y ` ge`0 USING begger's method :-`""^(11)C_(4)=330` |
|
| 3277. |
If vec(O)A = i + 3j - 2k, vec(O)B = 3i + j - 2k and C is a point on AB such that OC bisects angle AOB then vec(O)C = |
|
Answer» 4(i + J - K) |
|
| 3278. |
Are the following sets relation ? phi * B from phi to B. |
| Answer» SOLUTION :`PHI` to B from `phi` to B is a RELATION. | |
| 3279. |
A cruve is respresented by C=21x^(2)-6xy+29y^(2)+6x-58y-151=0 The lengths of axes are |
|
Answer» `6,2 sqrt(6)` `2(x-3y+3)^(2)+2(3x+y-1)^(2)=180` or `((x-3y+3)^(2))/(60)+((3x+y-1)^(2))/(90)=1` or `((x-3y+3)/(sqrt(1+3^(2))sqrt(6)))^(2)+((3x+y-1)/(3sqrt(1+3^(2))))=1` Thus, C is an ellipse whose lengths of AXES are `6,2sqrt(6)`. The minor and the major axes are `x-3y+3=0 and 3x+y-1=0`, respectively. Their point of intersection gives the CENTER of the center of the conic. THEREFORE, Center `-=(o,1)` |
|
| 3280. |
Statement-I : The distance of the normal to x^(2) + 2y^(2) = 5 at (1,sqrt(2)) from origin is 1/3sqrt(2).Statement-II : The product of the perpendiculars from the foci of the ellipse (x^(2))/(7)+(y^(2))/(4)=1to any tangent is 7.Statement-III: The distance between the foci of (x^(2))/(25)+(y^(2))/(36)=1 is 2sqrt(11). The Statements that are correct are : |
|
Answer» both I & III |
|
| 3281. |
If PSQ is a focal chord then match the ellipse with the valueof (1)/(SP)+(1)/(SQ)with the value of |
|
Answer» 2341 |
|
| 3282. |
There are 3 men, 2 women and 4 children. If 4 persons are selected then which of the following is/are true? |
|
Answer» Probability of SELECTING exactly 2 CHILDREN = `10/21` |
|
| 3283. |
Prove that : Find an approximate value of root(6)(63) correct to 4 decimal places. |
|
Answer» |
|
| 3284. |
If the sum to n terms of the series (3)/((1^(2))(2^(2)))+(5)/((2^(2))(3^(2)))+(7)/((3^(2))(4^(2)))+.... is (288)/(289), then n = |
|
Answer» |
|
| 3285. |
int((2+secx)secx)/((1+2secx)^2)dx= |
|
Answer» `(1)/("2 cosec x"+COTX)+C` `=int((2+cosx)cosx+SIN^(2)x)/((2+cosx)^(2))dx` `=int(cosx)/(2+cosx)dx-int(-sin^(2)x)/((2+cosx)^(2))dx` `=(SINX)/(2+cosx)+C` |
|
| 3286. |
The vectors bar(a) and bar(b) are unit vectors perpendicular to each other. The unit vector bar( c ) makes an angle theta with bar(a) and bar(b). If bar( c )=x bar(a)+y bar(b)+z(bar(a)xx bar(b)) then ……….. |
|
Answer» `x=cos THETA,y=sin theta,Z=COS2THETA` |
|
| 3287. |
If the complex numbers sin x + i cos 2 x and cos x - i sin 2 x are conjugate to each other, then x is equal to |
| Answer» Answer :D | |
| 3289. |
If a,b,c are in A.P. then the determinant {:|( x+2,x+3,x+2a),( x+3,x+4,x+2b),( x+4,x+5,x+2c)|:} is |
| Answer» ANSWER :A | |
| 3290. |
If 20 persons are sitting in a row, find the number of ways of selecting 3 persons out of them so that no two of the selected three are consecutive. |
|
Answer» |
|
| 3291. |
Draw the graph of the function f(x) = |(x+ (1)/(2))[x]|, -2 le x le 2, where [*] denotes the greatest integer function. Find the points of discontinuity and non-differentiability. |
|
Answer» Solution :Here, `""F(X)= |(x+ (1)/(2))[x]|, -2 le x le 2` `rArr""f(x)= {{:(|(x+(1)/(2))(-2)|",",, -2le xlt -1),(|(x+(1)/(2))(-1)|",",,-1LE xlt 0), (|(x+ (1)/(2))(0)|",",,0 le x lt1),(|(x+ (1)/(2))(1)|",",,1lexlt 2),(|(3)/(2)*2|",",,x=2):}` `rArr""={{:(-(2x+1)",",,-2lexlt-1),(-(x+1//2)",",,-1le x lt -1//2),((x+1//2)",",,-(1)/(2)le x lt 0),(0",",,0LE x lt 1),(x+ (1)/(2)",",,1 le x lt 2),(3",",,x=2):}` The graph of the function is as shown in the following figure. 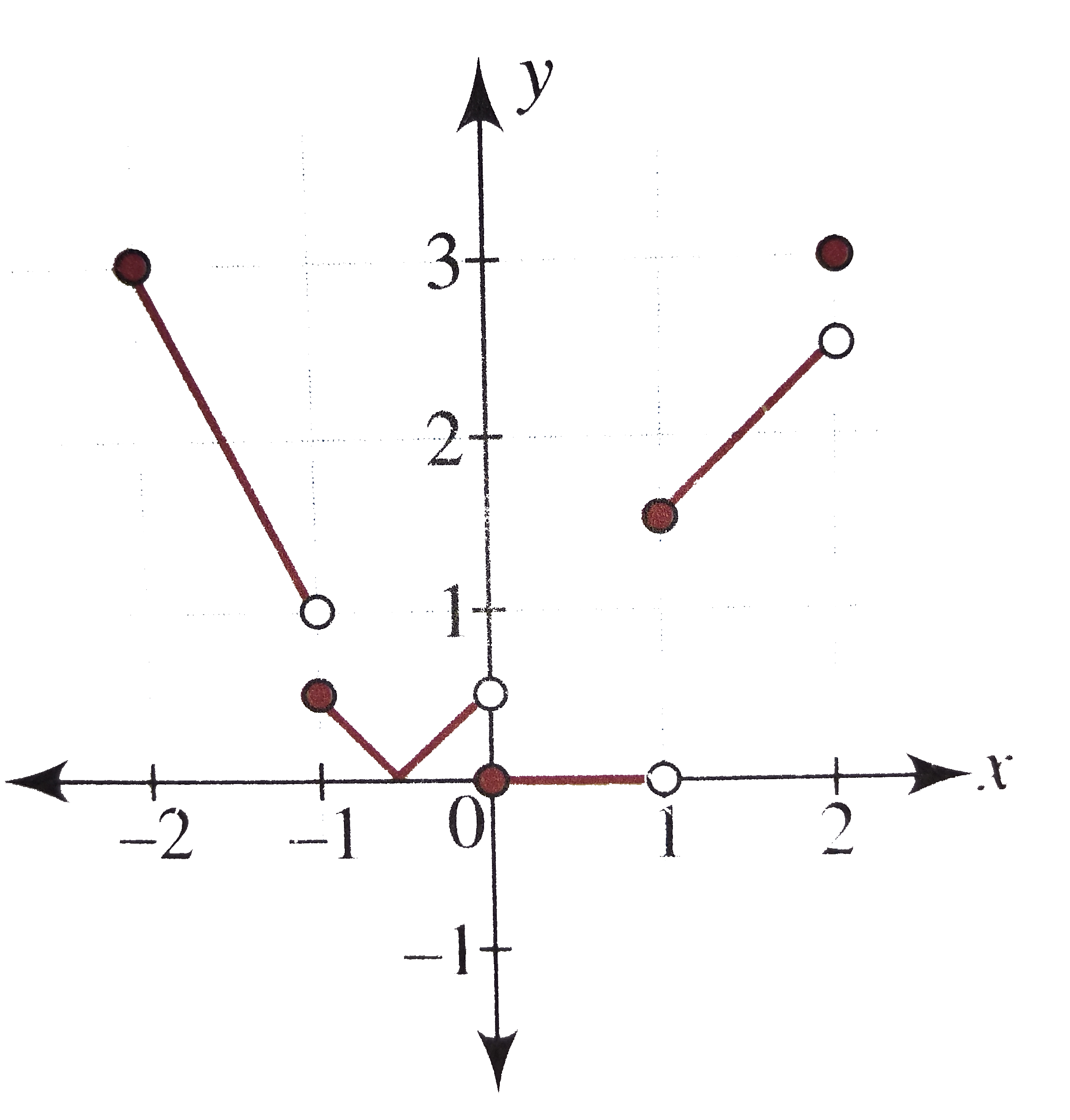 From the figure, `f(x)` is not continuous as `x= { -1, 0, 1, 2}` as at these points, the graph is broken and `f(x)` is not differentiable. At `x= {-1, (-1)/(2), 0, 1, 2}` as at `{-1, 0, 1, 2}`, the graph is broken and `x=-1//2`, there is a sharp edge. |
|
| 3292. |
Construct Collection of all fingers of a hand in the form of set and describe it with the help of proposition. |
| Answer» SOLUTION :If`{X:p_1 (x)} ={x:p_2(x)}`, SHOW each `x,p_1(x) `and` p_2(x)` have the same TRUTH VALUE. | |
| 3293. |
If f:A rarr B is a function defined by f(x)=(x^(2)-x)/(x^(2)+2x), then which one of the following is true? |
|
Answer» A = R - {0, -2}, B = R and f(x) is decreasing function |
|
| 3294. |
Quacky found a paper in which product of two non-zero digits(1 to 8) is given. Similarly, Mario got sum of the same two numbers and then they are having a conversation. 1. Quacky says "I don't know the numbers".Mario says "I don't know the numbers". 2. Quacky says "I don't know the numbers".Mario says "I don't know the numbers". 3. Quacky says "I don't know the numbers".Mario says "I know the numbers". What is the product of the numbers ? |
|
Answer» 6 1x4 = 2x2 1x6 = 2x3 1x8 = 2x4 2x6 = 3x4 2x8 = 4x4 3x8 = 4x6 After this MARIO tells he doesn't know, that means there are atleast two pair remaining inthe possibilities with the same sum: 1 + 4 = 2 + 3 2 + 8 = 4 + 6 2 + 6 = 4 + 4 1 + 6 = 3 + 4 1 + 8 3 + 8 2 + 2 2 + 4 Now in these 8 there are STILL 2pairs with same product.... 1x6 = 2x3 2x6 = 3x4 2x8 = 4x4 1x4 4x6 Now in the 6 there are atleast 2 PAIRS with same sum... 1 + 6 = 3 + 4 2 + 6 = 4 + 4 2 + 8 2 + 3 Now there are atleast 2 pairs with same sum... 2,6 3,4 1,6 4,4 The product of the possibilities is 12 which will be the answer |
|
| 3295. |
If A=[{:(2,-1,1),(-1,2,-1),(1,-1,2):}] Verify the result A^3-6A^2+9A-4I=O and hence find A^(-1) |
|
Answer» |
|
| 3297. |
If the equality int_(0)^(x) (bt cos 4t)/( t^2) dt = (a sin 4x)/( x) -1 holds for all x such that 0 lt x lt pi //4 then a and b are given by |
|
Answer» `a=1//4, b=1` |
|
| 3298. |
The perpendicular distance from the point 3i - 2j + k to the line joining the points I - 3j + 5k, 2i + j - 4k is |
| Answer» Answer :B | |
| 3300. |
If 2x^(2)+5xy+2y^(2)-11x-7y+K=0 is the pair of asymptotes of the hyperbola 2x^(2)+5xy+2y^(2)-11x-7y-4=0 then K= |
|
Answer» 3 |
|