InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3802. |
If the normal toy^(2) =4axat t_1 cuts the parabola again at t_2then |
|
Answer» ` t_2^(2)le 8` |
|
| 3803. |
Let f:Rto R be given by fx={{:(x^5+5x^4+10x^3,+10^2+3x+1,,xlt0,,),(,x^2-x+1,,0lexlt1,,),((2)/(3)x^3-4x^2+7x-(8)/(3),,,1lexlt3,,),((x-2)log_e(x-2),-x+(10)/(3),,xge3,,):} Then which of the following options is/are correct ? |
|
Answer» f is increasing on `(-oo,0)` `f(x)=[{:(x^25x^4+10x^3+10x^2+3x+1",",xlt 0),(""x^2-x-x+1",",0lexlt1),(""(2)/(3)x^3-4x^2+7x-(8)/(3)",",1lexlt3),(" "(x-2)log_e(x-2)-x+(10)/(3)",",xge3):}` So,`f(x)=[{:(5x^5+20x^3+30x^2+20x+3",",xlt 0),(""2x-1",",0ltxlt1),(""2x^2-8x+7", ",1ltxlt3),(""log_e(x-2)",",xgt3):}` At `x=1,f^(n)(1^-)=2 gt0 and f^n(1^+)=4-8=-4lt0` ` therefore f'(x)` is not differentiable at `x=1`, and f'(x) has a local maximum at `x=1`. For `x in (- oo ,0)` `f'(x)=5x^4+20x^3+30x^2+20x+3` and since, `f'(-1)=5-20+30-20+3=-2lt 0` So, `f(x)` is not increasing on `x in (- oo, 0)`. Now, as the range of function `f(x)` is R, so f is onto function. Hence, options (B) , (c) and (d) are correct. |
|
| 3804. |
The two adjacent sides of a parallelogram are 2 hat i - 4 hat j + 5 hat k and hat i - 2 hat j - 3 hat k.Find the unit vector parallel to its diagonal.Also, find its area. |
|
Answer» |
|
| 3805. |
Let P = sum_(r=1)^(50)(""^(50+r)C_(r)(2r-1))/(""^(50)C_(r)(50+r)), Q = sum_(r=0)^()(""^(50)C_(r))^(2), R = sum_(0)^(100)(-1)^(r)(""^(100)C_(r))^(2) If n is any positive integer, then findthe number whose square is ubrace(111..........1)_("2 times")-ubrace(222..........2)_("n times") |
|
Answer» |
|
| 3806. |
If vec(a) and vec(b) are two units vector inclined at an angle of (pi)/(3), then value of |vec(a) + vec(b)| is |
|
Answer» 1.equal to 1 |
|
| 3807. |
Using truth tables, determine wether the following statements are tautology or contradiction or contingency : (1) ~(~p^^~q)vvq (2) [(pvvq)^^~p]^^(~q) |
| Answer» | |
| 3808. |
One bag A contains 5 white and 3 black balls. Another bag B contains 6 white and 2 black balls. A card is drawn from pack of cards. If it is club card, a ball is drawn from bag A. If it is red card a ball is drawn from bag B. Otherwise he kept quiet. The probability of getting white ball is |
|
Answer» `(15)/(32)` |
|
| 3809. |
Consider the following distribution The sum of the mean deviation from the mean and the mean deviation from median of this distribution is |
| Answer» ANSWER :D | |
| 3810. |
Theorderand degreeofdifferentialequationxy (d^2 y)/( dx^2) +((dy)/(dx))^2-y((dy)/(dx))^3=0 is ……. |
| Answer» Answer :D | |
| 3811. |
Find by integration the volume of the container which is in the shape of a right circular frustum as shown in the figure. |
|
Answer» |
|
| 3812. |
Write down and simplify 7^("th")" term in"(3x-4y)^(10) |
|
Answer» |
|
| 3813. |
x +(x^2)/(3!)+(x^3)/(5!) + ......oo = |
|
Answer» `SQRTX ((E^(sqrtx)-e^(-sqrtx)))/2` |
|
| 3814. |
y = -e^(x) is |
|
Answer» CONCAVE up for `X GT 0` |
|
| 3815. |
lim_(n rarr oo)n^(-nk) {(n_+1)(n+1/2)(n+1/2)...(n+1/(2^(k-1)))}^n= |
|
Answer» `2` |
|
| 3816. |
Evaluate the following definite integrals : int_(0)^(pi/2)sin^(4)xdx |
|
Answer» |
|
| 3817. |
int x^(2) [sqrt(2)((pi)/(4)+x)+e^(x)]dx = |
|
Answer» `(x^(2) +2X - 2) SIN x + (-x^(2) +2x +2) COS x + (x^(2) - 2x + 2) E^(x) +C` |
|
| 3818. |
Find the area of the region bounded by y^(2) = 9x, x = 2, x = 4 and the x-axis in the first quadrant. |
|
Answer» |
|
| 3819. |
If A = [(1,2,2),(2,1,2),(2,2,1)], " then " A^(-1)= |
|
Answer» 4L-A |
|
| 3820. |
If bar(i), bar(j), bar(k) are unit vectors along the positive directionsof the coordinate axes, then shown that the four points 4 bar(i) + 5 bar(j) + bar(k), - bar(j) - bar(k), 3 bar(i) +9 bar(j) + 4 bar(k) and - 4 bar(i) + 4 bar(j) + 4 bar( k) are coplanar |
|
Answer» |
|
| 3821. |
2x^(2) |
|
Answer» `6x-4` `f(x+y)=f(x)+2y^(2)+"kxy for all "x,y in R` `Rightarrow (f(x+y)-f(x))/(y)=2y"+kx for all "x inR` `Rightarrow UNDERSET(y to 0)lim (f(x+y)-f(x))/(y)=underset(y to 0)lim (2y+kx)` `Rightarrow underset(y to 0)lim (f(x+y)-f(y))/(y)=underset(y to 0)lim (2y+kx)` `Rightarrow f'(x)=kx" for all "x in R` `Rightarrow f'(x)=kx" for all "x in R` But, f(1)=2 and f(2)=8. Therefore, `2=(k)/(2)+Cand 8=2k+C` `Rightarrow k=4 and C=0` HENCE, f(x)=`2x^(2)"for all "x in R` |
|
| 3822. |
If theta_1, theta_2, theta_3 are respectively the angles by which the coordinate axes are to be rotated to eliminate the xy term from the following equations, then the descending order of these angles is A_1 = 3x^2+5xy+3y^2+2x+3y+4=0 A_2= 5x^2+2sqrt(3) xy+3y^2+6 =0 A_3 =4x^2+sqrt(3) xy+5y^2-4 =0 |
|
Answer» `theta_1, theta_2 , theta_3` |
|
| 3824. |
While defining inverse trigonometric functions , a new system is followed where co-domains has been redefined as follows : sin^(-1)(-x) is equal to |
|
Answer» `NPI` |
|
| 3825. |
Draw the graph of the function f(x) = 2x^(2)-log_(e)|x| |
|
Answer» Solution :We have `f(x) = 2x^(2)-log_(e)|x|, x ne 0` Clearly, `f(x)` is an even function, HENCE its graph is SYMMETRICAL about the y-axis. `underset(xto 0^(+))"lim"(2x^(2)-log_(e)|x|)=infty` and `underset(x to +-infty)"lim"(2x^(2)-log_(e)|x|)=infty` (as difference between the value of `2x^(2)` and ln`|x|` is infinite, `log_(e)|x|` increases very slowly, but `2x^(2)` increases faster) ALSO `f^(')(x) = 4x-1/x = (4x^(2)-1)/(x)` `f^(')(x)=0 RARR x = +-1/2` From the limiting values of the function at x=0 and at inifinity, we can conclude that `x=+-1/2` are points of minima. From the above discussion, the graph of the function is as shown in the FOLLOWING figure. 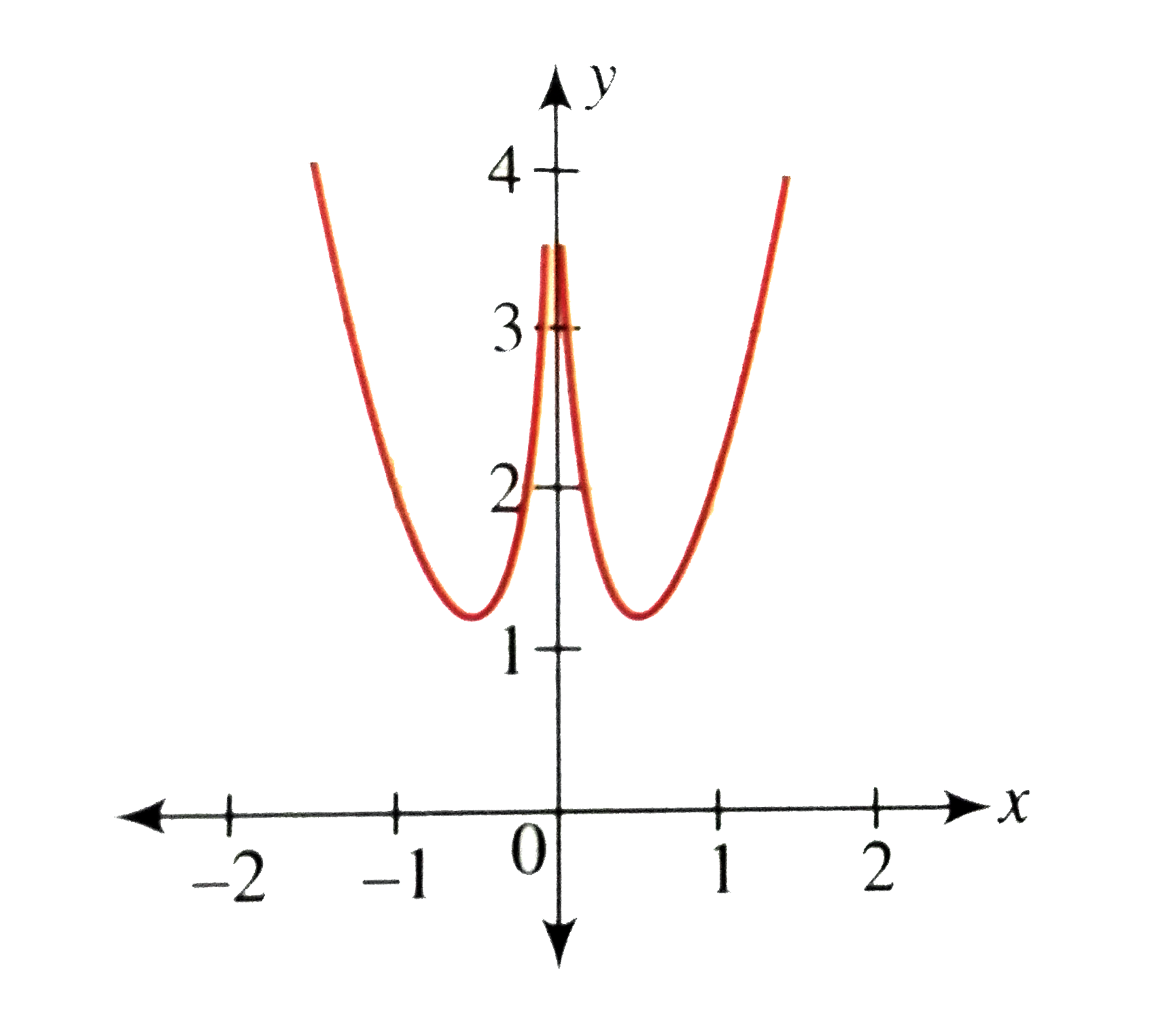
|
|
| 3826. |
While defining inverse trigonometric functions , a new system is followed where co-domains has been redefined as follows : If f(X)=3sin^(-1)x-2cos^(-1)x then f(x) is |
|
Answer» `cos 2x is 3/5` |
|
| 3827. |
While defining inverse trigonometric functions , a new system is followed where co-domains has been redefined as follows : The minimum of (sin^(-1)x)^(3)+(cos^(-1)x))^(3)is equal to |
|
Answer» `-sin^(-1)X` |
|
| 3828. |
From 6 men and 4 women a committee of 5 members is to be formed. The probability that this can be done so as to include atleast one woman always is |
|
Answer» `(1)/(42)` |
|
| 3830. |
Let A be 3xx3 symmetric invertible matrix with real positive elements. Then the number of zero elementsin A^(-1) are less than or equal to : |
|
Answer» 0 |
|
| 3831. |
By using the properties of definite integrals, evaluate the integrals int_(0)^(pi/4)log (1 +tan x) dx |
|
Answer» `PI/8 LN 2` |
|
| 3832. |
Let the complex numbers z_(1),z_(2),z_(3)" and "z_(4) denote the vertices of a square taken in order. If z_(1)=3+4i" and "z_(3)=5+6i, then the other two vertices z_(2)" and "z_(4) are respectively |
|
Answer» `5+4i, 5+6i` |
|
| 3833. |
If the maximum value of x which satisfies the inequality sin^(-1)(sinx) ge cos^(-1)(sinx)" for "x in (pi)/(2), 2pi" is " lambda, then (2lambda)/(3) is equal to (take pi=3.14) |
|
Answer» |
|
| 3834. |
What is the value of 6t such that volume contained inside the planes sqrt(1-t^(2))x+tz=2sqrt(1-t^(2)), z=0,x=2+(tsqrt(4t^(2)-5t+2))/(sqrt(12(1-t^(2))^(1//4))) and |y|=2 is maximum. |
|
Answer» When we cut these planes by the plane `y=0`, the triangle OBTAINED is `ABC`, where `AB=(tsqrt(4t^(2)-5+2))/(SQRT(12)(1-t^(2))^(1//4))` LET `CAB=theta=` angle between first and `xy` plane, the `costheta=t` 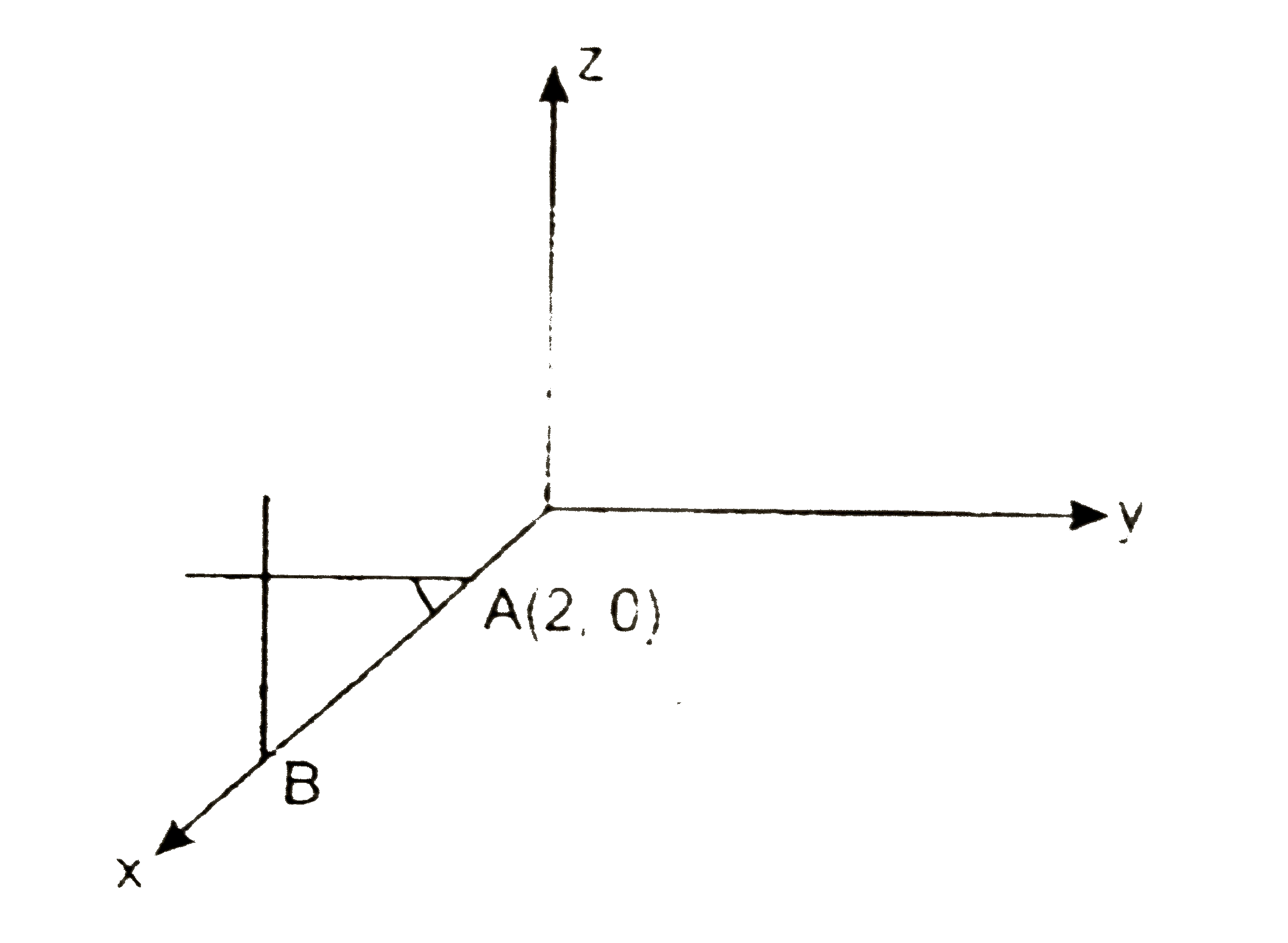 Area of `DeltaABC=Delta=1/2(AB)^(2)tantheta` `Delta=1/2(t^(2)(4t^(2)-5t+2))/(12(1-t^(2))^(1/2))XX(sqrt(1-t^(2)))/t=1/2 (4t^(3)-5t^(2)+2t)/12` For example `(dDelta)/(dt)=0implies12t^(2)-10t+2=0` `impliest=(10+-sqrt(100-96))/24=1/2` or `1/3` Now, `(d^(2)Delta)/(dt^(2))=24t-10` So, `Delta`"is maximum at"`t=1/3`"and minimum at "`t=1/2` `:. t=1/3` |
|
| 3835. |
Prove that : Find the coefficient of x^(12)" in "(1+3x)/((1-4x)^(4)). |
|
Answer» |
|
| 3836. |
If alpha=9vec(i) -vec(j) +2vec(k) and beta= vec(i)+2vec(k) , then find the value of alpha . beta |
| Answer» | |
| 3837. |
If alpha=9vec(i) -vec(j) +2vec(k) and beta= vec(i)+2vec(k) , then find the value of alpha xx beta |
| Answer» | |
| 3838. |
Product R ............ |
Answer» 
|
|
| 3839. |
The partial fractions of (1)/((x^(2)+9)(x^(2)+16)) are |
|
Answer» `1/7 [ (1)/(x^(2)+9)-(1)/(x^(2)+16)]` |
|
| 3840. |
If alpha=5vec(i) -3vec(k) and beta= 2vec(i)-vec(j)+2vec(k) , then find the value of alpha xx beta |
| Answer» | |
| 3841. |
Which option (s) is/are ture ? |
|
Answer» `f :R to R, f (X) =e ^(|x|)-e ^(-x)` is many-one into FUNCTION |
|
| 3842. |
Find : int(5x-2)/(1+2x+3x^2)dx. |
|
Answer» |
|
| 3843. |
If P(A) = (6)/(11), P(B) = (5)/(11) and probability of at least one of the event = (7)/(11), then P((B)/(A)) isA) (6)/(11)B)(4)/(5)C)(2)/(3)D) 1 |
| Answer» Answer :C | |
| 3844. |
A bag B_(1) white balls and 2 red balls. Another bag B_(2) has 4 white and 6 red balls. A ball is drawn fandomly from bag B_(1) and without seeing its colour, is put in bag B_(2). Now a ball is drawn from bag. B_(2). The probability of both the drawn balls, being of the same colour, is |
|
Answer» `(41)/(55)` |
|
| 3845. |
Find the equation of the perpendicular bisector of the segment joining the points 7+7i, 7-7i in the Argand diagram. |
| Answer» | |
| 3846. |
Find the point of intersection of the line (x-1)/(2)=(2-y)/(3)=(z+3)/(4) and the plane 2x + 4y - z = 1. Also find the angle between them. |
|
Answer» |
|
| 3847. |
Find all points of discontinuityof f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):}. |
| Answer» | |
| 3848. |
Find the solution of sin^(-1)(x/(1+x))-"sin"^(-1)(x-1)/(x+1)="sin"^(-1)1/(sqrt(1+x)) |
|
Answer» |
|
| 3849. |
Evaluate the following lim_(xto1)(x^2-2x+1)/(x^2-x) |
|
Answer» SOLUTION :`lim_(xto1)(X^2-2x+1)/(x^2-x)` `lim_(xto1)(x-1)^2/(x(x-1))` `lim_(xto1)(x-1)/x=0/1=0` |
|
| 3850. |
For the ellipse x^(2)/(25)+(y^(2))/(16)=1 a list of lines given in List I are to be matched with their equations given in Lisht II. The correct match is: |
|
Answer» `{:(,,i,ii,III),(,a,B,a,e):}` |
|