InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3701. |
Using the property of determinants andd without expanding in following exercises 1 to 7 prove that |{:(-a^2,ab,ac),(ba,-b^2,bc),(ca,cb,-c^2):}|=4a^2b^2c^2 |
|
Answer» |
|
| 3702. |
Solve abs(x-1) gt 1 and represent the solution on the number line. |
|
Answer» Solution :`abs(x-1) gt 1` `rArr -1 gt x-1 gt 1` `rArr 0 gt x gt 2` `rArr x lt 0` and `x gt 2` `therefore` The solution set is S = {x:x `in` R, x `lt`0 and x `gt` 2} = `(-infty, 0) CUP (2, infty)` we can SHOW this solution in number line as 
|
|
| 3703. |
Forevery twice differentiablefunction f(x)the valueof |f(x)| le 3 AA x in R and for some alpha f(alpha) + (f'(alpha))^(2) =80. Number of integral values that (f'(x))^(2) can takebetween (0,77) are equal to "________" |
|
Answer» |
|
| 3704. |
int_0^(pi/4) xsinxdx |
|
Answer» Solution :`int_0^(pi/4) xsinxdx` [integrating by PARTS taking xas FIRST and sinx as second function] `[x-(-cosx)]_0^(pi/4)-int_0^(pi/4)(-cosx)DX` `(-pi/4)cos(pi/4)+[sinx]_o^(pi/4)` `(-pi/4)cos(pi/4)+sin(pi/4)-sin0=(1/sqrt2)(1-(pi/4))` |
|
| 3705. |
If (1+i) is a root of the equation x^(2)-x+(1-i)=0, then the other root is |
|
Answer» `1-i` |
|
| 3706. |
Find the angle between the lines whose d.c's are related by l + m + n = 0 & l^(2) + m^(2) - n^(2) = 0 |
|
Answer» |
|
| 3707. |
Find the maximum or minimum values of the following expressions on R i) x^(2) + 6x – 27 ii) 3x^(2) + 2x + 7 iii) x^(2) - 12x + 32 iv) 2x^(2) + 3x + 1 |
|
Answer» |
|
| 3708. |
If the height of the cone is constant then find the rate of change of its curved surface area with respect to its radius. |
|
Answer» |
|
| 3709. |
Let a,b and c be distinct real numbers. If a,b,c are in geometric progression and a+b+c=xb, then x lies in the set |
|
Answer» (1,3) |
|
| 3710. |
p ^^ (q ^^ r) is logically equivalent to |
|
Answer» <P>`p VV (q ^^ r)` |
|
| 3711. |
Find number of othe ways in which word 'KOLAVARI' can be arranged, if allvowels are separate from each other ? |
|
Answer» 289 |
|
| 3712. |
If the function f(x)=sin^(-1)x+cos^(-1)x and g(x) are identical, then g(x) can be equal to |
|
Answer» `sin^(-1)|x|+|cos^(-1)x|` If `g(x)=|sin^(-1)x|+cos^(-1)|x|={{:(-sin^(-1)x +pi-cos^(-1)x, -1le x lt 0),(=pi-(pi)/(2)=(pi)/(2)),(sin^(-1)x + cos^(-1)x, 0LE x le 1),(=(pi)/(2)):}` |
|
| 3713. |
A company sells its product at the rate of Rs. 6 per unit. The variable costs are estimated to run 25% of the total revenue received. If the fixed costs for the product are Rs. 4500. Find the total cost function. |
|
Answer» |
|
| 3714. |
Find the value of |{:(cos((2pi)/(63)),,cos((3pi)/(70)),,cos((4pi)/(77))),(cos((pi)/(72)),,cos((pi)/(40)),,cos((3pi)/(88))),(1,,cos((pi)/(90)),,cos((2pi)/(99))):}| |
|
Answer» Solution :`Delta= |{:(cos((pi)/(7)-(pi)/(9)),,cos((pi)/(7)-(pi)/(10)),,cos((pi)/(7)-(pi)/(11))),(cos((pi)/(8)-(pi)/(9)),,cos((pi)/(8)-(pi)/(10)),,cos((pi)/(8)-(pi)/(11))),(cos((pi)/(9)-(pi)/(9)),,cos((pi)/(9)-(pi)/(10)),,cos((pi)/(9)-(pi)/(11))):}|` `|{:(cos((pi)/(7)-(pi)/(9)),,cos((pi)/(7)-(pi)/(10)),,cos((pi)/(7)-(pi)/(11))),(cos((pi)/(8)-(pi)/(9)),,cos((pi)/(8)-(pi)/(10)),,cos((pi)/(8)-(pi)/(11))),(cos((pi)/(9)-(pi)/(9)),,cos((pi)/(9)-(pi)/(10)),,cos((pi)/(9)-(pi)/(11))):}|` `=0` |
|
| 3715. |
Value of lamda so that point (lamda,lamda^(2)) lies between the lines |x+2y|=3 is |
|
Answer» `(-1/2,2)` 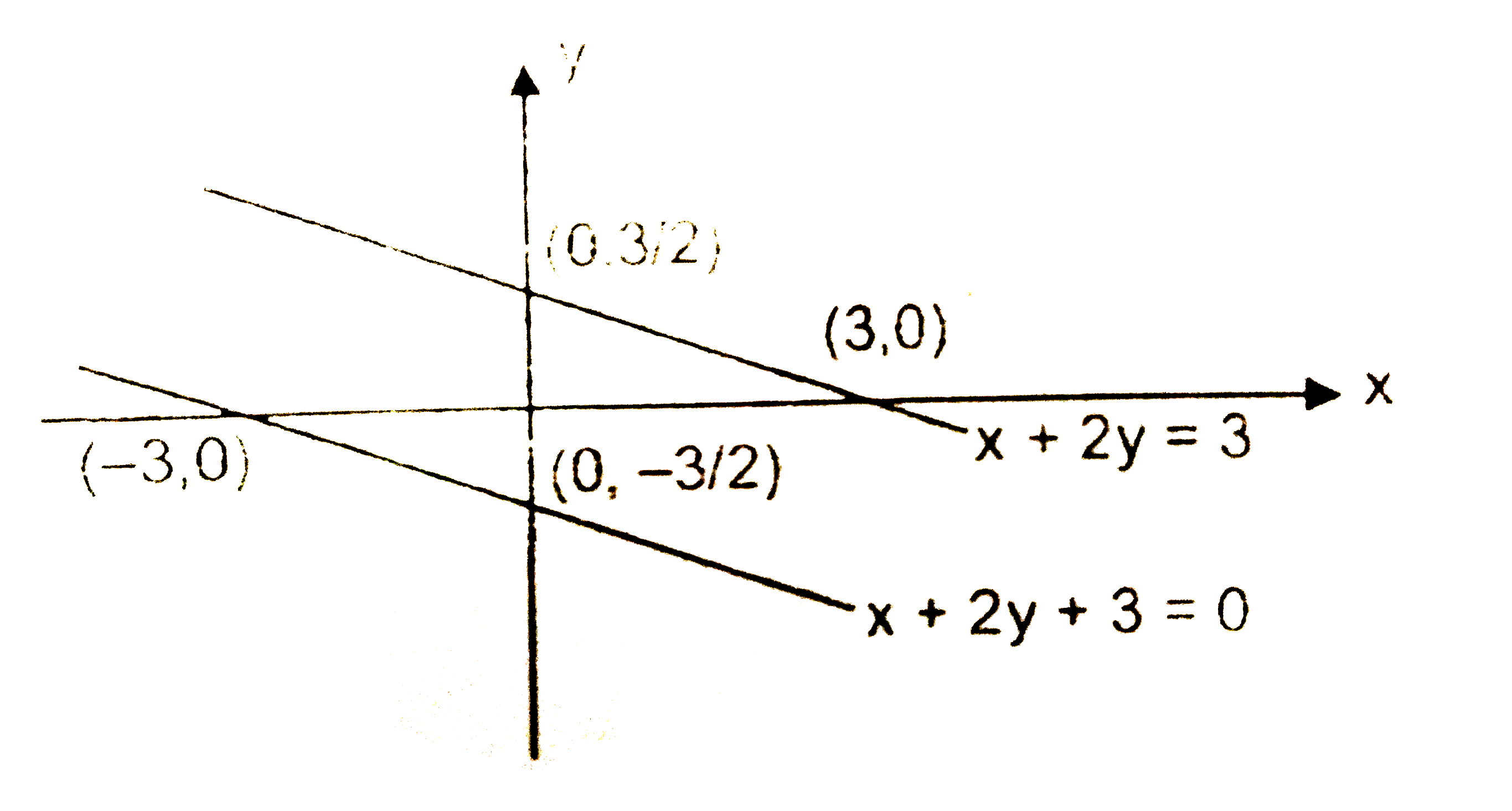 `2lamda^(2)+LAMDA+3gt0implieslamdaepsilonR` `2lamda^(2)+lamda+3gt0implieslamdaepsilonR` `2lamda^(2)+lamda-3lt0` `lamda EPSILON(-3/2,1)` |
|
| 3717. |
The number of ways in which 5 boys and 3 girls can be seated on a round table if a particular boy B_(1)and a particular girl G_(1)never sit adjacent to each other is |
|
Answer» `7!` |
|
| 3718. |
Identify the quantifier in the following statements and write the negation of the statement.(iii)There exists a capital for every state of india |
| Answer» SOLUTION :There EXISTS | |
| 3719. |
Find the domain and range of those relations in a which are functions. {(a,2),(b,1),(c,1)} |
| Answer» SOLUTION :RANGE of the FUNCTION is {1,2} | |
| 3720. |
Equation of plane passing through (1,1,1) and the line of intersection of planes x+2y-z+1=0 and 3x-y-4z+3=0 is |
|
Answer» 8X+ 5Y - 11Z +8=0 |
|
| 3721. |
If a straight line through C(-sqrt(8),sqrt(8)) making an asngle 135^(@) with the x-axis and cuts the circle x=5cos theta, y = 5 sin theta in points A and B AB= |
|
Answer» 5 |
|
| 3722. |
There are 15 bulbs in a room .Each one of them can be operated independently .The number of ways in which the room can be lighted |
|
Answer» `8^(5)-1` |
|
| 3723. |
If overline(a), overline(b), overline(c) are non-coplanar vectors and overline(a)=lambda(overline(b)timesoverline(c))+mu(overline(c)timesoverline(a))+gamma(overline(a)timesoverline(b)) then lambda= |
|
Answer» `(OVERLINE(a)*overline(B))/([[overline(a), overline(b), overline(C)]])` |
|
| 3724. |
The smallest positive integer p for which expression x ^(2)- 2px +3p[+4 is negative for atleast one real x is: |
|
Answer» 3 |
|
| 3725. |
If1 , omega , omega^(2) are the cube roots of unity , then find the values of the following . ( 1 - omega + omega^(2))^(3) |
|
Answer» |
|
| 3726. |
If the lines 2x+3y+12=0, x-y+k=0 are conjugate with respect to the parabola y^(2)=8 then k is equal to |
| Answer» ANSWER :C | |
| 3727. |
The sum of two non - zero numbers in 12. The minimum sum of their reciprocals is ………… |
|
Answer» `(1)/(10)` |
|
| 3728. |
lim_(xto0)(sqrt(1+xsinx)-sqrt(cosx))/(tan^(2)2x)= |
| Answer» ANSWER :D | |
| 3729. |
In theinteriorof aforestthereare someapes . Oftheirtotalnumbersquareof1/9thareplayingat oneplace. Theremainingare onthehills. Thetotalnumberof apesis |
|
Answer» 27 or 54 |
|
| 3730. |
If theanglesof triangleare in theratio4 :1:1 , thentheratioof thelongestsideto the perimeter is |
|
Answer» `SQRT(3) :2 + sqrt(3)` |
|
| 3731. |
If p =a + bomega + comega^(2),q = b + comega+ aomega^(2), and r =c + aomega +bomega^(2), where a,b,c ne 0 and omega is the complex cuberoot of unity , then . |
|
Answer» If p,Q,r lie on the CIRCLE|z|=2, the trinagleformed by these POINTIS equilateral. `therefore p +q+ r = (a+b+c)(1+ omega + omega^(2))=0` p,q,r lie on the circle `|z|=2`, whosecircumcenter is origin. Also `(p+q+ r)//3=0` . Hence the cenroidwith cicumcenter. So, the triangle is equilateral. Now ,`(P +q+ r)^(2)= 0` `rArr p^(2) +q^(2) + r^(2) = -2pqr[(1)/(p)+(1)/(q) +(1)/(r)]` `=-2pqr[(1)/(a+bomega+comega^(2))+(1)/(omega(bomega^(2)+c+aomega^(2)))+(1)/(c+aomega +bomega^(2))]` `=2pqr[(1)/(omega^(2)(aomega +bomega^(2)+c))+(1)/(omega(bomega^(2) + c+ aomega))+(1)/(c+aomega+bomega^(2))]` `(-2pqr)/(aomega+ bomega^(2)+c)[(1)/(omega^(2))+(1)/(omega)+ (1)/(1)]= 0""(2)` Hence `p^(2)+q^(2) + r^(2) = 2` (pq + qr + rp)` |
|
| 3732. |
Number of ways of selecting two squares having common side in a chess board is (1 unit size squares) |
|
Answer» 112 |
|
| 3734. |
Approximately whatpercent of the mining industries' average annual production from 1991 - 1995 came from production of aluminium? |
| Answer» Answer :D | |
| 3735. |
If z = 3- 5i then z^(2) - 10z + 30= |
|
Answer» 20i-16 |
|
| 3736. |
If A = {a,b,c,d} and the function f ={(a,b),(b,d) , (c,a) ,(d,c) } . Write f^(-1). |
|
Answer» |
|
| 3737. |
show that the matrix A=[[0,1,-1],[-1,0,1],[1,-1,0]] is a skew symmetric matrix |
| Answer» SOLUTION :`A^T = [(0,-1,1),(1,0,-1),(-1,1,0)] = -[(0,1,-1),(-1,0,1),(1,-1,0)] = -A therefore A` is skew symmetric | |
| 3738. |
Show thatthe functionf : N to Ndefinedby f(x) = {[x-1 \ if \x \ is \ even], [x +1 \ if \ x is \ odd]} is one-oneand onto. |
|
Answer» SOLUTION :Suppose `f(x_(1))= f(x_(2))` Case 1when`x_(1) ` isodd and `x_(2)`is even In THISCASE `f(x_(1)) =f(x_(2)) rArr x_(1) +1 =x_(2)-1` `rArr x_(2) - x_(1)=2` Thisis acodtradicationsince thatdifferencebetween anodd interger and anevenintegercan neverbe 2. Thusin this case`f(x_(1))NE f(x_(2))` Similarlywhen `x_(1)`is evenand `x_(2)`is oddthen `f(x_(1)) ne f(x_(2))` Case 2when `x_(1)" and " x_(2)`are bothodd In thiscase`f(x_(1))=f(x_(2)) rArr x_(1)+ 1 =x_(2) -1` `rArr x_(1)=x_(2)` `:.` f isone-one Case 3When `x_(1) " and " x_(2)`are both even In thiscase `f(x_(1))=f(x_(2))rArr x_(1) -1 =x_(2) -1` `rArr x_(1)= x_(2)` `:.`f is one-one In orderto showthat FIS ontolet `y in N`(the codomain) Case 1 wheny is odd In thiscase `(y +1)` is even `:. f( y+1) =(y+1)-1 =y` Case 2wheny is even In thiscase `(y-1) ` is odd `:. f (y-1)=y-1 +1=y` Thuseach `y in N`(codomain of f)has itspre-imagein dom (f) `:. ` f is onto. Hence f is one-oneonto. |
|
| 3740. |
Prove that the radius of the circle whose centre is (-4,0) and which cuts the parabola y^(2) = 8x at A and B such that its common chord AB subtends a right angle at the vertex of the parabola is equal to ''4''. |
|
Answer» |
|
| 3741. |
Let a triangle ABC be inscribed in a circle of radius 2 units. If the 3 bisectors of the angles A, B and C are extended to cut the circle atA_(1), B_(1) and C_(1) respectively, then the value of[(A A_(1) "cos"(A)/(2)+ B B_(1) "cos"(B)/(2)+C C_(1) "cos"(C)/(2))/(sin a + sin B + sin C)]^(2)= |
|
Answer» 4 |
|
| 3742. |
Statement 1 : Consider the statements p : Delhi is in India q : Mumbai is not in Italy Then the negation of the statement p vv q, is 'delhi is not in India and Mumbai is in Italy' Statement 2: For any two statement p and q ~(p vv q) = ~p vv ~q |
|
Answer» Statement 1 and statement 2 are both false |
|
| 3743. |
If overline(a)*overline(b)=overline(b)*overline(c)=overline(c)*overline(a)=0, then overline(a)*(overline(b)timesoverline(c))= |
|
Answer» a non-zero vector |
|
| 3744. |
By using the properties of definite integrals evaluate the integrals in exercise. overset(1)underset(0)int x(1-x)^(n)dx |
|
Answer» |
|
| 3745. |
Let f(x)=0 be a polynomial equation with real coefficients. Then between any two distinct real roots of f(x)=0, there exists at least one real root of the equation f'(x)=0. This result is a consequence of the celebrated Rolle's theorem applied to polynomials. Much information can be extracted about the roots of f(x)=0 from the roots of f'(x)=0. If the roots of x^(3)-12x+k=0 lie in (-4, -3),(0, 1) and (2, 3), then the range of valuesof k is |
|
Answer» `4 lt K lt 11` |
|
| 3746. |
If the solutoin of the differential equation e^(x/y(1-y^(2)))[y (dx)/(dy)-x]+[xy^(2)+y^(3)(dx)/(dy)]=0 is Ae^(xy)+Be^(x/y)+C=0, Then A+B is |
|
Answer» `-1` `d(e^(xy))+d(e^(x/y))=0` `e^(xy)+e^(x/y)+c=0` `A+B=1` |
|
| 3747. |
If the sum of first three numbers in G.P. is 21 and their product is 216 , then the numbers are |
|
Answer» 3,6,12 |
|
| 3748. |
The solution of (xdx + ydx)/(x^(2) + y^(2)) = 0 is |
|
Answer» LOG(XY) = c |
|
| 3750. |
Fundamental theorem of definite integral : int_(0)^(pi/4)(sin^(9)x)/(cos^(11)x)dx=........ |
|
Answer» `(1)/(2)` |
|