Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 701. |
A solid cylinder and a thin-walled hollow cylinder have the same mass and radius. They are rolling horizontally toward the bottom of an incline. The center of mass of each has the same translational speed. The cylinders roll up the incline and reach their highest points. Calculate the ratio of the distances (S_("Solid")//S_("hollow"))along the incline through which each center of mass moves. |
|
Answer» `(4)/(3)` |
|
| 702. |
A magnetic field in a certain region is given by vecB=B_0 cos (omegat) hatkand a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=pi/(2omega), pi/omega and t=(3pi)/(2omega). |
Answer» Solution :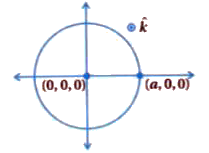 Magnetic flux linked with coil, `phi=vecB.vecA=BA cos theta = BA` `phi=B_0 (pia^2)cos omegat[ because A=pia^2]` Induced emf, `epsilon=(dphi)/(dt)=-d/(dt) (B_0 pia^2 cos omegat)` `=-B_0 pia^2 [-omega sin omegat]` `epsilon=B_0 pia^2 omega sin omegat` Induced current `I=epsilon/R=(B_0 pia^2 omega)/R sin omegat` At `t=pi/(2OMEGA)`time, `I=(B_0pia^2omega)/R sin(omegaxxpi/(2omega))` `I=(B_0 pi a^2 omega)/R` Now according to `vecB = B_0 cos (omegat) hatk`magnetic flux came out from coil decreases (cos is decreasing FUNCTION for t = 0 to `t =pi/omega` ). Hence, according to Lenz.s law induced current will try to increase that outward flux. For that induced current will flow in anticlockwise direction so at (a, 0, 0) current is along `+HATJ` direction. At `t=pi/omega` time `I=(B_0 pi a^2 omega)/R sin (omegaxx pi/omega)=0` At `t=(3pi)/(2omega)` time `I=(B_0 pia^2 omega)/R sin (omegaxx(3pi)/(2omega))` `=(B_0 pi a^2 omega)/R sin ((3pi)/2)` `I=-(B_0 pia^2 omega)/R` Negative SIGN appearing here indicates that induced current at (a, 0, 0) is in `-hatj` direction. [According to CASE (i)] |
|
| 703. |
Two wires having different densities are joined at x = 0. An incident wave y_(1) = A_(1) sin(omegat - k_(1)x),travelling to the right in the wire is partly reflected and partly transmitted at x=0. If A_(t)and A_t be the amplitudes of reflected and transmitted waves respectively, |
|
Answer» `y_(r) = A_(r) sin(omega t + k_(1)X)` |
|
| 704. |
A certain prism of refracting angle 60^@ and of refractive index '2' is immersed in a liquid of refractive index sqrt2, then the angle of minimum deviation will be |
| Answer» ANSWER :A | |
| 705. |
Three non-conducting infinite planes of charge A, B, and C are vertical and parallel to one another. There is a uniform electric field vec(E)_(p) to the right of plane C. The field vec(E)_(p) points to the left and the field vec(E)_(p) to the right of plane C. The field vec(E)_(p) pointsto the left and the field vec(E)_(p) points to the right. The signs of the charges on the plates A, B and C may be |
|
Answer» `-,-,-` |
|
| 706. |
What is electric dipole ? Write its SI unit. |
|
Answer» Solution :An electric DIPOLE is a system of TWO equal and opposite point charges separated by a finite distance. If .2a. is the distance betweentwo charges q and `-q` the dipole MOMENT of this system is given by `vecp =q(2veca)`Electric dipole moment is a vector quantity, its direction is pointing towards POSITIVE charge.  The unit of electric dipole moment is Cm (Coulomb-meter) or Ampere-second meter. Its dimensional formula is `M^(0)L^(1)T^(1)A^(1)` and `M^(0)L^(1)T^(0)Q^(1)`. Total charge of the dipole system is zero. But its electric field is non-zero because two opposite charges are situated at DIFFERENT places. |
|
| 707. |
Spontaneous and continuous disintegrationof a nucleus of aheavy element with the emission of certain types of radiation is known as radioactivity:-Write the relation connecting half-life and mean life of radioactive element. |
| Answer» SOLUTION :The number of nuclei undergoing DECAY PER unit time is PROPORTIONAL to number of nuclei in the sample at that time. | |
| 708. |
The potential energy of a particle of mass m is given by U(x)={:(E_0,0lexle1),(0," "x gt1):} lambda_1 and lambda_2 arethe de-Broglie wavelengths of the particle, when 0 le x le 1 and x > 1 respectively. If the total energy of particle is 2E_0. find (lambda_1//lambda_2)^2 |
|
Answer» 1 `lambda_1=h/sqrt(2mE_0)` KE=`2E_0` (for x > 1), `lambda_2=h/sqrt(4mE_0), lambda_1/lambda_2=sqrt2` |
|
| 709. |
A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as xy- plane. Its magnetic moment overset(to)(m)….. |
|
Answer» is non-zero and points in the z-direction by symmetry. Magnetizing CURRENT flows in its ring on the ring surrounding the toroid ring but current I inside the toroid is zero, hence magnetic moment m = 0. For larger distance r outside the toroid `m prop (1)/(r^3)` but it is not possible for toroid. |
|
| 710. |
The following figure shows an equilateral triangle, each side of which has length of 2.00 cm. Point charges are fixed to each corner, as shown. The 4.0 mu C charge experiences a net force due to the charges q_(A) and q_(B). This net force points vertically downward and has a magnitude of 405 N. Determine the magnitudes and algebraic signs of the charges q_(A) and q_(B). |
|
Answer» `q_(A) = -2.60 MU C`,`q_(B) = -2.60 mu C` |
|
| 711. |
A short bar magnet placed with its axis at 30^@ with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 xx 10^(-2) J. What is the magnitude of magnetic moment of the magnet? |
|
Answer» Solution :Here `THETA= 30^@ , B = 0.25 T and TAU = 4.5 xx 10^(-2) J` From the relation `tau= m B sin theta , ` we have Magnetic MOMENT of the MAGNET `m= (tau)/(B sin theta) = (4.5xx10^(-2))/(0.25xxsin 30^@) = 0.36 J T^(-1)` . |
|
| 712. |
Consider the followingtowstatementI ad II . (I) Paramagentismis explainedby domain theory . (II) Susceptiblity of a diamagnetic substacnein independentof temperature.Identifythe correctchoiceformthe follwing . |
|
Answer» BOTHI and II are correct |
|
| 713. |
A : If a current has both ac and dc components, then a dc ammeter used to measure this current will measure the average value of the total current. R : The scale of a dc ammeter is uniformly divided. |
|
Answer» If both Assertion & Reason are TRUE and the reason is the correct EXPLANATION of the assertion, then mark (1) |
|
| 714. |
Binding energy of ""_2He^4 and ""_3Li^7 nuclei are 27.37 MeV and 39.4 MeV respectively. Which of the two nuclei is more stable? Why? |
| Answer» SOLUTION :`""_2He^4` because its BE/nucleon is GREATER | |
| 715. |
A n-p-n transistor is said to be in active region of operation, when |
|
Answer» both EMITTER and collector JUNCTIONS are FORWARD BIASED. |
|
| 716. |
A particle of 2m is projected at an angle of 45°with horizontal with a velocity of 20sqrt(2) m/s. After 1 sec. explosion takes place and the particle is broken into two equal pieces. As a result of expansion one point comes to rests. The maximum height from the ground attained by the other part is(g=10m//s^(2)) |
|
Answer» Solution :`u_(x) = 20sqrt(2) XX 1/sqrt(2) = 20m//s, u_(y) =20sqrt(2) xx 1/sqrt(2) = 20 m//s` After 1s `u_(x) = 20 m//s, V_(y) = u_(y)-"gt"=20 -10 = 20 m//s` DUE to explosion one part comes to rest `2m(20hati + 10 hatj) =m.0 + mvecV, vecV = 40 hati + 20 hatj` `V_(y)^(1) = 20m//s, therefore H_(2) = V_(y)^(2)/(2g)` HEIGHT attained after explosion `=(20 xx20)/(2 xx 10) = 20 m` But height attained before Explosion `=ut -1/2"gt"^(2)` `=20 xx t + 1/2 xx 10 xx 1^(2) = 15 mH = 15+20 = 35 m` |
|
| 717. |
In the circuit shown in figure the heat produced in the 5 ohm resistor due to the current flowing through it is 10 calorie per second. The heat generated in the 4 ohm resistor is |
Answer» Solution :`V_(AB)=I_(2)(4+6)`,  `THEREFORE V_(AB)=10I_(2)` `"Also"V_(AB)=I_(1)(5)`, `therefore 5I_(1)=10I_(2) or I_(2)=2I_(2)` `"LET"H=I^(2)R,""therefore (H_(4))/(H_(5))=(I_(2)^(2)xx4)/(I_(1)^(2)xx5)` `(H_(4))/(10)=(I_(2)^(2)xx4)/((2I_(2))^(2)xx5) or H_(4)=(10xx4)/(4xx5)=2("cal")/("sec")` |
|
| 718. |
Prove that high frequency a.c. can pass through a pure capacitor easily but not through pure inductor. |
|
Answer» SOLUTION :Inductive REACTANCES `X_L = 2pifL` i.e.,`X_L prop f` CAPACITIVE reactance `X_c = 1/(2pifC)` i.e.,`X_c prop 1/f` |
|
| 719. |
Find the wavelength of the short-wave limit of an X-ray continuous spectrum if electrons approach the anticathode of the tube with velocity v = 0.85 c, where c is the velocity of light. |
|
Answer» SOLUTION :The wavelength of `X`-rays is the least when all the `K.E.` of the electrons approaching the anticathode is converted into the ENERGY of `X-`ray. But the `K.E.` of electron is `T_(m) = mc^(2) [(1)/(sqrt(1-v^(2)//c^(2)))-1]` `(mc^(2) =` rest mass energy of electrons `= 0.511MeV`) THUS `(2pi cancelh c)/(lambda) = T_(m)` or `lambda = (2pi cancelh c)/(T_(m)) = (2pi cancelh)/(mc) [(1)/(sqrt(1-v^(2)//c^(2))-1)]^(-1)` `= (2picancelh)/(mc(gamma-1)), gamma = (1)/(sqrt(1-v^(2)//c^(2))) = 2.70 PM` |
|
| 720. |
Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid ? |
| Answer» Solution :When REFRACTIVE INDEX of LIQUID is EXACTLY same as the refractive index of glass. | |
| 721. |
In the aboveproblem ,At what distancefrom the centrewill the first maximum be located ? |
|
Answer» 0.021 CM on ONE SIDE and 0.028 cm on the other side |
|
| 722. |
The radioactivity of given sample of whiskey due to tritium (Half life= 12 yrs ) was found to be only 3.125% that measured in a recently purchased bottle marked " 10 years old", By how many years age the sample must have been prepared ? |
|
Answer» Solution :`m/m_(0) =1/(2^n)implies (3.125)/(100) =1/(2^n)n = 5 = t/T` `t = 5T = 5XX 12 = 60` years . `:.` Total AGE of SAMPLE `= 60+10=70` years |
|
| 723. |
Explain that for a greater distance, the spreading due to diffraction dominates over due to ray optics. |
|
Answer» Solution :An APERTURE of size .a. illuminated by a parallel beam sends diffracted light into an angle `theta` , then angular width `theta~~(lamda)/(a)` In travelling a distance z, the diffracted beam acquires a width `=ztheta` `=(zlamda)/(a)` DUE to diffraction The value of z the spreading due to diffraction is equal to the size of a of the aperture. `:.a=(zlamda)/(a)` `:.z=(a^(2))/(lamda)` This quantity is called the Fresnel distance `z_(F)`. `:z_(F)=(a^(2))/(lamda)` This equation shows that for distances much smaller than `z_(F)` the spreading due to diffraction is smaller compared to the size of the beam (That means moving in a straight line). Hence, spreading due to diffraction DOMINATES over that due to RAY optics and it shows that ray optics is VALID in the limit of wavelength tending to zero. |
|
| 724. |
A cup of coffee cools from 150^@ F to 144^@ F in I min in a room temperature at 72^@ F. How much time with the coffee take to cool from 110^@ F to 104^@ F in the same room? |
|
Answer» 1.55 min ` T_2 = 150^@ F, T_2 = 144^@ F, t_1 = 1` min androom temperature, `T_0 = 72^@F` According to Newton's law of cooling, ` mc ( (T_1 - T_2) )/(t_1) = K ( (T_1+ T_2)/(2)- T_0)` ` mc ( (150 - 144)/(1) ) = K ( (150 + 144 )/(2)- 72 )` 6 mc = 75K.....(i) In second case `T_1 = 110^@ F, T_2 = 104^@F` TIME ` = t_2 =? ` By Newton's law of cooling, we have ` mc ( (110 - 104)/(t_2) ) = K ( (110 + 104)/(2) - 72) ` ` (6mc)/(t_2) = 35k`...(ii) From Eqs. (i) and (ii), we get ` (6mc)/( (6mc)/(t_2) ) = (75K)/(35K)` `RARR t_2 = 15/7 = 2.14` min |
|
| 725. |
State Gauss theorem in electrostatics. Derive the expression for electric field at a point due to an infinitely long straight charged conductor. |
|
Answer» Solution :Statement: The total electric flux through a closed SURFACE in free space is equal to `(1)/(epsi_0) `times the net charge enclosed by the surface. `phi = (q)/( epsi_0)` Derivation :  In the above fig. AB is the infinitely long WIRE E is the electric field P is a point at a distance r from the wire . r. is the radius of GAUSSIAN cylinder .l is the length of the Gaussian cylinder Let .q. be the charge enclosed by the Gaussian cylinder. Let .`lamda `. be the linear charge density on the wire. Flux through the end faces is zero because there are no components of electric field ALONG the normal to the end faces. `phi = ` flux tħrough curved surface `phi = E xx `area of curved surface `(phi =E xx` area) `phi= E xx2pi rl to(1)` From Gauss.s theorem `phi =(q)/(epsi_0) to (2)` but ` lamda= (q)/(I)= q= lamda I` `(2)= phi =(lamda I)/( epsi_0 )to( 3) ` On comparing (1) and (3), we get `E xx 2 pi rI=(lamda I )/( epsi_0)` ` E= ( lamda )/(2 pi r epsi_0)` ` E=(1)/( 2 pi r epsi_0 )(lamda )/(r)` The direction of .E. is perpendicular to the wire and directed away from the wire. |
|
| 726. |
One ideal cell is used to drive current in a metre bridge circuit. In an experiment x is the balancing length obtained. If we replace the wire of the metre bridge with another wire of material having more rsistivity and lesser diameter, the new balancing length will be |
|
Answer» LESS than x |
|
| 727. |
An alternating voltage given by V= 140 sin 314 t is connected across a pure resistor of 50 2. Find (i) the frequency of the source. (ii) the rms current through the resistor. |
|
Answer» Solution :(i) As alternating voltage is GIVEN by `V = 140 sin 314 t` and `R = 50 Omega` `therefore` PEAK voltage `V_(m) =140 V` and angular FREQUENCY `omega = 314 rad s^(-1)` `therefore` Frequency `v= omega/(2pi) = 314/(2 xx 3.14) = 50 Hz` (ii) rms voltage `V_(rms) = V_(m)/sqrt(2) = 140/sqrt(2) V` `therefore` rms voltage `I_(rms) =V_(rms)/R = 140/(sqrt(2) xx 50) = 1.98 A` |
|
| 728. |
Give some of the commonly known ideas regarding magnetism. |
|
Answer» Solution :Some of the commonly known ideas regarding MAGNETISM are as below : (i) The EARTH behaves as a magnet with the magnetic field pointing approximately from the geographic SOUTH to the north. (ii) When a BAR magnet is freely suspended, it points in the north-south direction. The tip which points to the geographic north is called the north pole and the tip which points to the geographic south is called the south pole of the magnet. (iii) There is a repulsive force when north poles (or south pole) of two magnets are brought close together and there is an attractive force between the north pole of one magnet and the south pole of the other. (IV) We cannot isolate the north or south pole ofa magnet. If a bar magnet is broken into two halves, we get two similar bar magnets with somewhat weaker properties. Unlike electric charges, isolated magnetic north and south poles known as magnetic monopoles do not exist. (v) It is possible to make magnets out of iron and its alloys. |
|
| 729. |
A tank is filled with water to a heigth of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope t be 9.4 cm. what is the refractive index of water ? If water is replaced by a liquid of refractive index 1.63 upto the same hight, by distance would the microscope have to be moved to focus on the needle again? |
|
Answer» Solution :` n_(WA)= ("REAL DEPTH")/("Apparent depth") = (12.5)/(9.4) = 1.33 "" n_("is") = (12.5)/(d_(l)) = 1.63` `therefore d_(l) = (12.5)/(1.63) = 7.66` CM i.e., depth in liquid = 7.66 cm Distance through which microscope has to be moved = 9.4 - 7.66 = 1.74` cm |
|
| 730. |
In double slit experiment, SS_2 is greater than SS_1 by 0.25 lamda . Calculate the path difference between two interfering beams from S_1 and S_2 for minima and maxima on the screen. |
|
Answer» SOLUTION :PATH difference between interfering waves `(SS_1 + S_2P) - (SS_1 + S_1P)` ` = (S_2P - S_1 P) + (SS_2 - SS_1)` ` d/D lamda + 0.25 lamda` For MAXIMUM ` d/D y + 0.25 lamda = N lamda` or` d/D y = ( n- 0.25) lamda` for minimum` d/D y + 0.25 lamda` ` (2n +1 ) lamda/2` ` d/D y = (2n +1) lamda/2 - 2 xx 0.25 xx lamda/2` `d/D y = (2n + 0.5) lamda/2` 
|
|
| 731. |
The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the forces between neutron and proton in deuteron as given in the form of a Coulomb force but with an effective charge e': F=1/(4piepsilon_(0)) (e'^(2))/r^(2) estimate the value of (e'//e) given that the following binding energy of a deuteron is 2.2MeV. |
|
Answer» 1.89 Replacing e by e' and m by m', reduced mass of neutron- proton `m'=(MxxM)/(M+M)=M/2="1836m"/2`=918 m …(ii) (M = mass of neutron / proton ) `therefore ` Binding energy , `E'=(918 me'^4)/(8 epsilon_0^2 h^2)`=2.2 MeV Dividing (ii) by (i) `918("e'"/e)^4=(2.2xx10^6)/13.6` `(e')/e=(176.21)^(1//4)` =3.64 |
|
| 732. |
A car drives along straight level frictionless road by an engine delivering constant power. Then velocity is directly proportional to |
|
Answer» t |
|
| 733. |
What we call when spectrum of absorbed light ? |
| Answer» SOLUTION :ABSORPTION SPECTRUM | |
| 734. |
What is modified ampere's sircuital law ? |
| Answer» Solution :It states that the line integral of the magnetic field `VECB` over a closed PATH is equal to `mu_0` TIMES the SUM of CONDUCTION current `I_C` and the displacement current `(I_D)` threading the closed path. `ointvecB.vecdl = mu_0 (I_C+I_D) | |
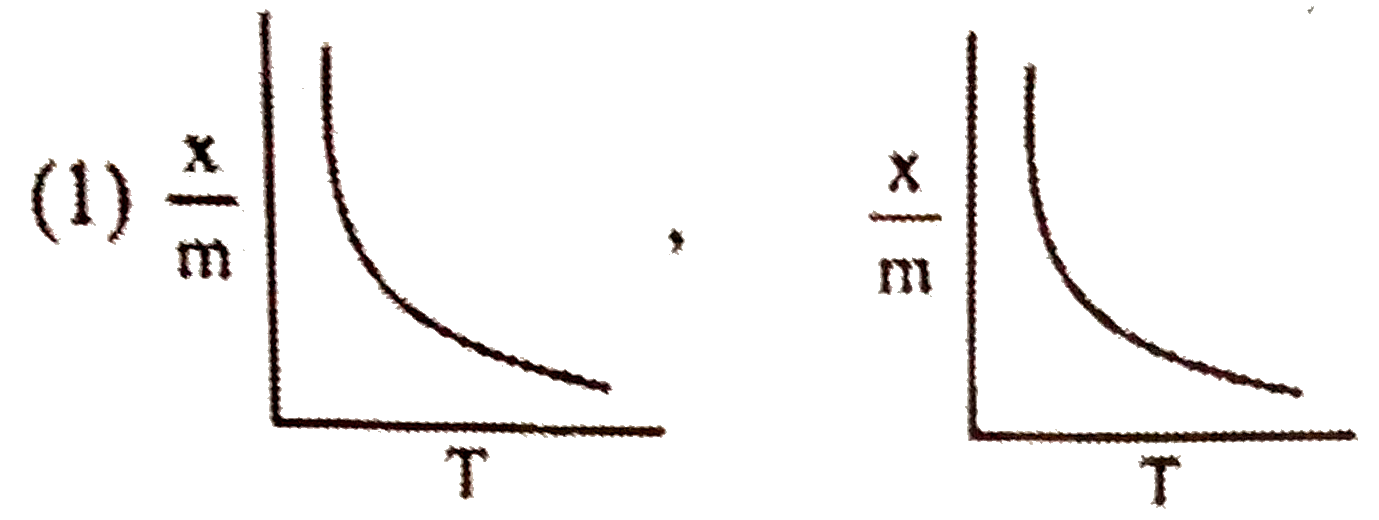
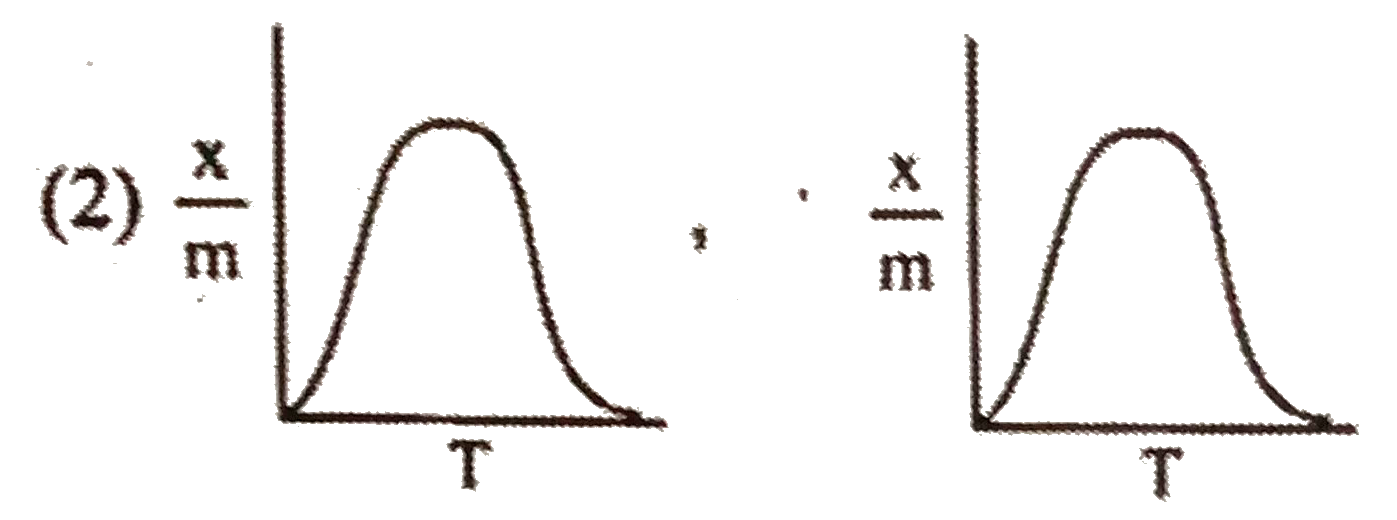
| 735. |
Select correct adsorption isobars for chemisorption and physisorption respectively : (where x/m = extent of adorption, T = temperature ) |
|
Answer»
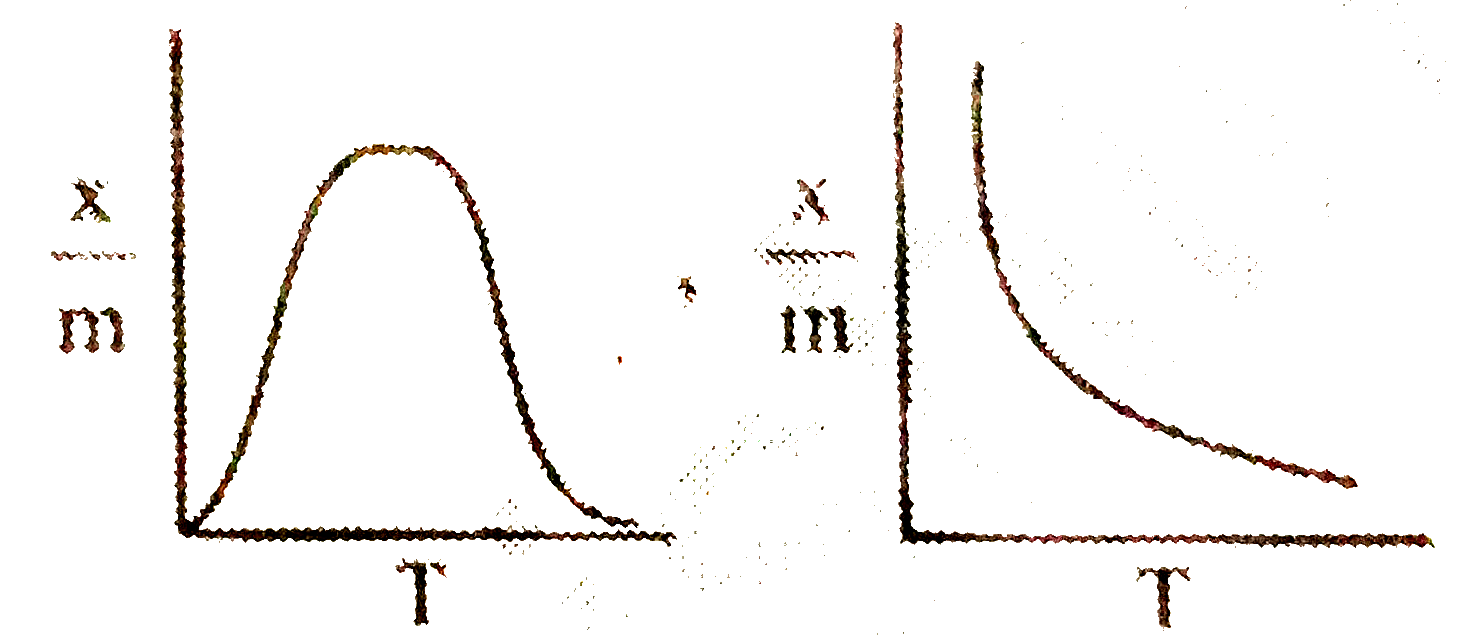
|
|
| 736. |
A ball falls vertically with a momentum 'p' and then bounces for large number of times before coming to rest. The total momentum imparted by ball to floor is (e = coff. of restitution): |
|
Answer» <P>`p(1+e)` |
|
| 737. |
A : In viewing through a magnifying glass, angular magnification decreases if the eye is moved back. R : Angle subtended at the eye becomes slightly less than the angle subtended at the lens. |
|
Answer» If both Assertion & Reason are true and the reason is the correct EXPLANATION of the assertion, then mark (1). |
|
| 738. |
Match the facts given in Column - I with the system given in Column - II |
|
Answer» |
|
| 739. |
In Example 3.1. the electron drift speed is estimated to be only a few mm s^(-1) for currents in the range of a few amperes ? How then is current established almost the Instant a circuit is closed ? |
|
Answer» Solution :When a BATTERY is connected across a conducting wire, electric FIELD is found to be established in that wire almost with a speed of light. This causes instantaneous local drift of every free electron and that too with a tremendous acceleration because its value given by a = `(eE)/(m)` is found to be very large (becausem being MASS of electron is extremely small equal to `9.1 xx 10^(-31) `kg) Hence all the free electrons start drifting simultaneously which produces instantaneous current in the wire. This current achieves its steady value WITHIN a very short time. (That is why bulb gets on almost at the same moment when we switch it on). |
|
| 740. |
An L-C-R series circuit with R = 100Omega is connected to a 200 V, 50 Hz A.C. source when only the capacitance is removed, the current lags the voltage by 60^@. When only the inductance is removed, the current leads the voltage by 60^@. Find the current in the circuit. |
|
Answer» `4 A` `therefore` tan `60^@ =X_L/R=sqrt3 rArr X_L=sqrt3R`….(1) Removing inductor C-R circuit is prepared where phase difference `|delta|=60^@` `therefore tan 60^@ = X_C/R = sqrt3 rArr X_C=sqrt3R`....(2) From (1) and (2) `X_L = X_C rArr omegaL=1/(omegaC)` means RESONANCE circuit is prepared `therefore Z=R rArr I_(rms) = V_(rms)/R` `=200/100`=2A |
|
| 741. |
Figure shows a rod of length resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity . Find the velocity of the other end B downward when the rod makes an angle with the horizontal. |
|
Answer» Solution :In such type of problems, when velocity of one PART of a body is given and that of other is required, we first FIND the relation between the two displacements, then differentiate them with respect to time. Here if the distance from the corner to the point is x and up to B is y. Then `v=(dx)/(DT)& v_(B)=(dy)/(dt)` (-sign denotes that y is DECREASING) `2x(dx)/(dt)+2y(dy)/(dt)=0 "" xv= yv_(B)` `v_(B)=(v)=(x)/(y) v cot theta` |
|
| 742. |
Figure shows a cross-section of a large metal sheet carrying an electric current along its axis. The current in a strip of width is k where k is a constant. Find the magnetic field at apoint P at adistance x From the metal sheet. |
Answer» Solution :Consider two strips R and S of the sheet SITUATED symmetrically on the two sides of P. The magnetic field at P above sheet and below sheet is parallel to sheet as shown in figure. There is no field perpendicular to the sheet.   Now applying Ampere.s LAW to the closed path 1-2-3-4-1 as shown in fig. `oint vecB.d vec(l) = mu_0 i_("in")` `int_(1)^(2)vecB.vec(dl) + int_(2)^(3) vecB.vec(dl) + int_(3)^(4) vecB.vec(dl) = mu_0 (kl)` or `BL+ 0 + Bl +0 = mu_0klor B = (mu_0k)/(2)` |
|
| 743. |
Suggest a method to locate IC for the following situations: (a) Given the velocity of a point on the body and the angular velocity of the body. (b) Given the lines of action of two nonparallel velocities. (c) Given the magnitude and direction of two parallel velocities. |
|
Answer» Solution :(a) In this case, if `vecv_(B)` and `omega` are KNOWN, the IC is located along the line drawn perpendicular to at `vecv_(B)` at B, such that the distance from B to the IC is `vecr_(B//C) = v_(B)//omega`, Fig. Note that the IC lies on that side of B which causes rotation about the IC, which is consistent with the direction of motion caused by `omega` and `vecv_(B)`. (b) Given the lines of action of two nonparallel velocities. Consider the body in Fig., where the lines of action of the velocities `vecv_(A)` and `vecv_(B)`are known. Draw two lines from points A and B that are perpendicular to `vecv_(A)` and `vecv_(B)` : Extending these PERPENDICULARS to their point of intersection as shown locates the IC at the instant considered. The magnitudes `vecr_(A//"IC")` and `vecr_(B//"IC")` are generally determined from the geometry of the body and trigonometry. FURTHERMORE, if the magnitude and sense of `vecv_(A)` are known, then the angular velocity of the body is determined from `vecv_(A) = omegavecr_(A//"IC")` Once computed, `omega` can then be used to determine `vecv_(B) = vecr_(B//"IC")`. (c) When the velocities of points A and B are par ALLEL and have known magnitudes `vecv_(A)` and `vecv_(B)` then the location of the IC is determined by proportional triangles. Examples are shown in Fig.In both cases, `vecr_(A//"IC") = vecv_(A)//omega` 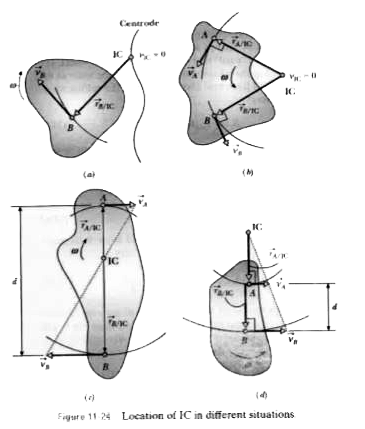 and `vecr_(B//"IC") = vecv_(B)//omega` . If d is a known distance between points A and B, then in Fig, `vecr_(A//"IC") + vecr_(B//"IC")=d`and in Fig.`vecr_(A//"IC") - vecr_(B//"IC")=d`. As a special case, note that if the body is translating, `vecv_(A) = vecv_(B)`, and the IC WOULD be located at infinity, in which case `vecr_(A//"IC") = vecr_(B//"IC")to oo` . This being the case, `omega=v_(A)//oo = v_(B)//oo = 0` as expected. = |
|
| 744. |
Pick the correct options. |
|
Answer» All electrons have magnetic moment. |
|
| 745. |
Light passes through a closed cylindrical tube containing a gas. If the gas is gradually pumped out, the speed of light inside the tube will |
|
Answer» increase |
|
| 746. |
A uniforme magnetic field of 1.5T exists in a cylindrical region of radius 10.0 cm. Its direction parallel to te axis along east to west. A wire carrying current of 7.0a. In the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire is turned from N-S to northeast-northwest direction. |
|
Answer» Solution :If `l_(1)` be the effective length of the WIRE INSIDE the magnetic field, `F_(2)=IBl_(1) sin45^(@)=Ibl["SINCE" l_(1) sin 45^(@)=l]` `=1.57xx7xx0.2=2.1N` (directed VERTICALLY downward) |
|
| 747. |
A uniforme magnetic field of 1.5T exists in a cylindrical region of radius 10.0 cm. Its direction parallel to te axis along east to west. A wire carrying current of 7.0a. In the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, that wire in the N-S direction is lowered from the axis by a distance of 6.0cm. |
Answer» Solution :When the wire is LOWERED by 6 cm from the axis then the effective length of the wire inside the MAGNETIC field is 2a [Fig. 1.98]. From FIGURE `a=8` cm `F=IB*2a=1.5xx7xx0.16N` `=1.68N` (directed VERTICALLY DOWNWARDS) |
|
| 748. |
A uniforme magnetic field of 1.5T exists in a cylindrical region of radius 10.0 cm. Its direction parallel to te axis along east to west. A wire carrying current of 7.0a. In the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire intersects the axis |
| Answer» Solution :`F_(1)=IBL sin 90^(@)=1.5xx7xx0.2xx1=2.1N` (DIRECTED vetically downwards) | |
| 749. |
A loop of a string of mass per unit length is U and radius R is rotated about an axis passing throughcentre perpendicular to the plane with an angular velocity omega . A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance for a stationary observer is x R omega . Find 'x |
|
Answer» |
|
| 750. |
An astronomical telescope of ten - fold angular magnification has a length of 44 cm. The focal length of the objective is |
| Answer» ANSWER :B | |