Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

801.

The phenomenon of spontaneous emission of radiations (alpha,beta and gammarays) from radioactive substances is called what ?

Answer»

SOLUTION :RADIOACTIVITY
Discussion
802.

A plane monochromatic light wave of intensity I_(0) falls normally on an opaque screen with a long slit having a semicircularcut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P. Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P.

Answer»

Solution :we apply the formula of problem `5.103` and calculate
`underset("aperture")int (a_(0))/(r ) E^(-ikr) dS = underset("semicircle")int + underset("SLIT")int`
The contribution of the full `1^(st)` Fresnel zone has been evaluated in `5.103`. The contribution the semi-circule is one half of it and is
`-(2pi)/(k)i a_(0)e^(-ikb) =- ia_(0) lambda e^(-ikb)`
The contribution of the slit is
`(a_(0))/(b) underset(0)overset(0.90sqrt(b lambda))int e^(-ikb) e^(-ik(x^(2))/(2b)) dx underset(-oo)overset(oo)int e^(-iky^(2)//2b) dy`
Now `underset(-oo)overset(oo)int e^(-iky^(2)//2b) dy = underset(-oo)overset(oo)int e^(-i(piy^(2))/(b lambda)) dy`
`sqrt((b lambda)/(2)) underset(-oo)overset(oo)int e^(-ipiy^(2)//2) du = sqrt(b lambda) e^(-ipi//4)`
Thus the contribution of the slit is
`(a_(0))/(b) sqrt(b lambda) e^(-ik b-i pi//4)underset(-oo)overset(0.9 xx sqrt(2))int e^(-i piu^(2)//2) du sqrt((b lambda)/(2))`
`= a_(0)lambda e^(-ikb-ipi//4) (1)/(sqrt(2))underset(0)overset(1.27)int e^(-ipiu^(2)//2) du`
Thus the INTENSITY at the OBSERVATION point `P` on the screen is
`a_(0)^(2)lambda^(2) |-i+(1 - i)/(2)(C(1.27) - iS(1.27))|^(2) = a_(0)^(2)lambda^(2) |-i + ((1-i)(0.67 - 0.65i))/(2)|^(2)`
(on using `(C(1.27) = 0.67` and `S(1.27) = 0.65)`
`= a_(0)^(2) lambda^(2)|-i + 0.01 - 0.66i|^(2)`
`a_(0)^(2)lambda^(2)|0.01 - 1.66i|^(2)`
`= 2.76 a_(0)^(2)lambda^(2)`
Now `a_(0)^(2)lambda^(2)` is the intensity due to half of `1^(st)` Fresnel zone and is therefore equal to `I_(0)`. (It can also be obtained by doing the `x`-intergal over `-oo` to `+oo`).
Thus `I = 2.76 I_(0)`.
Discussion
803.

A rectangular loop of sides 8cm and 2cm with a small cut is kept stationary in a uniform magnetic field directed normal to the loop. The current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3T at the rate of 0.02T^(-1). If the cut is joined and the loop has a resistance of 1.6 Omega, how much power is dissipated by loop as heat ? What is the source of this power ?

Answer»

SOLUTION :`6.4 XX 10^(-10)W`
Discussion
804.

The number of terminals in a transistor is :

Answer»

ONE
TWO
THREE
four

Answer :C
Discussion
805.

For a paramagnetic material, the dependence of the magnetic susceptibility x on the absolute temperature T is given as

Answer»

`X PROP R`
`X prop (L)/(T^(2))`
`x prop (l)/(T)`
`x prop T^(2)`

Discussion
806.

When an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the intermal energy of gas is:

Answer»

`(5)/(7)`
`(3)/(7)`
`(3)/(5)`
`(2)/(5)`

SOLUTION :Here increase in internal energy.
`Delta U =n C_(v)dT`.
Heat supplied at CONSTANT pressure.
`Delta Q =n C_(P)dT`.
`therefore (Delta U)/(Delta Q)=(C_(v))/(C_(P))=(1)/(gamma) =(1)/(7//5)=(5)/(7)`
Thus, correct choice is (a).
Discussion
807.

An infinite line charge produces a fiedl of 9xx10^(4)NC^(-1) at a distance of 2xx10^(-2)m. Calculate the linear charge density.

Answer»

Solution :(a) `1.45 xx10^(-3) C`
(B) `1.6 xx10^(8) NM^(2)//C`
Discussion
808.

A neutron with velocity v suffers head on elastic collision with the nucleus of an atom of mass number A at rest. The fraction of energy retained by neutron is

Answer»

`((A+1)/(A))^(2)`
`((A+1)/(A-1))^(2)`
`((A-1)/(A+1))^(2)`
`((A-1)/(A))^(2)`

Solution :Here `m_(1)=m_(1) m_(2)=Am,u_(1)=u,u_(2)=0`
`:.` velocity of neutron after collison is
`V=((m_(1)-m_(2))u_(1)+2m_(2)u_(2))/(m_(1)+m_(2))=((m-Am)u)/(m+Am)=((1-A)u)/((1+A))`
`:.` K.E. of neutron after collison, `1/2 m_(1)v_(2)`
or `E_(1)=1/2m_(1)((1-A)/(1+A))^(2)u^(2)` and K.E. before collison,
`E_(1)=1/2"mu"^(2)`
`:. (E_(1))/(E_(1))=(1/2M((1-A)/(1+A))^(2)u^(2))/(1/2mu^(2))=((1-A)/(1+A))^(2)`
Discussion
809.

In the circuit shown in figure B_(1), B_(2) and B_(3) are identical bulbs and C is a parallel plate capacitor. (a) Which bulb is brightest? (b) If separation between the plates of the capacitor is increased very slowly to double its value, how does the brightness of each of the bulbs change ?

Answer»


ANSWER :(a) B1
(B) No CHANGE
Discussion
810.

Transverse wave possesses the property of

Answer»

YONG modulus
modulus of rigidity
Bulk modulus
volume elasticity

Answer :B
Discussion
811.

A hollow metal sphere is filled with water and is hung by a long thread. It is made to oscillate. If water slowly flows through a small hole in the bottom, how wll the period of oscillation be affected ?

Answer»

the period will GO on decreasing till the sphere is empty
the period will go on INCREASING till the sphere is empty
the period will remain unchanged throughout
the period will FIRST increase, then it will decrease till it is empty and the period will be finally the same as when the sphere was full of water.

Answer :D
Discussion
812.

The B-H curve of a ferromagnetic material is as shown in figure :Identify the value of retentivity and coercivity from the figure.

Answer»

SOLUTION :Ob REPRESENTS RETENTIVITY and Oc COERCIVITY.
Discussion
813.

Show that if one collision takes place in every tau seconds then the resistivity is given by rho=(m)/(ne^(2)rho, where all the terms have their usual meaning.

Answer»


ANSWER :N//A
Discussion
814.

When a piece of aluminium wire of finite length is drawn through a series of dies to reduce its diameter to half its value, its resistance will become

Answer»

2 TIMES.
4 times.
8 times.
16 times

Answer :D
Discussion
815.

A 10 mu F capacitor is in series with a 50 Omega resistance and the combination is connected to a 220 V, 50 Hz line. Calculate (i) the capacitivereactance, (ii) the impedance of the circuit and (iii) the current in the circuit.

Answer»

Solution :Here, `C = 10 mu F = 10 xx 10^(-6) = 10^(-5)F`
(i) Capacitive reactance,
`X_(C) = (1)/(omega C) = (1)/(2pi v C) = (1)/(2 xx 3.14 xx 50 xx 10^(-5)) = 318.5 Omega`
(ii) Impedance of CR CIRCUIT.
`Z_(CR) = sqrt(R^(2) + X_(C)^(2)) = sqrt((50)^(2) + (318.5)^(2))`
`= 322.4 Omega`
(III) Current, `I_(rms) = (E_(rms))/(Z_(CR)) = (220)/(322.4) = 0.68 A`
Discussion
816.

Statement-1: For the calculation of gravitational force between any two uniform spherical shells, they can always be replaced by particles of same mass placed at respective centres. Statement-2: Gravitational field of a uniform spherical shell out side it is same as that of particle of same mass placed at its centre of mass.

Answer»

Statement-1 is TRUE, statement-2 is true and statement-2 is correct explanation for statement-1.
Statement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.
Statement-1 is true, statement-2 is false.
Statement -1 is false, statement -2 is true.

Solution :They cannot be replaced by point masses if they are kept inside one ANOTHER.
Discussion
817.

The decimal number 53 is equal to the binary number :

Answer»

110101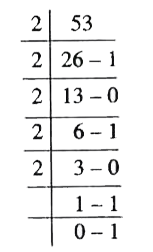
101101
101010
111111

Solution :
`:. (53)_(10)=(110101)_2`
Discussion
818.

(a) Write symbolically the beta-decay process of phosphorus. (b) Derive an expression for the average life of a radionuclide. Give its relationship with the half-life.

Answer»

Solution :(a) `BETA-` decay PROCESS
`""_(15)^(32) P to ""_(16)^(32) S + beta^(-) + bar(v) "or"_(15)^(32) P to ""_(16)^(32) X + ""_(-1)e^(0) + bar(v)`
(b) Derivation of AVERAGE life :
`tau = (lambda N_(0) int_(0)^(**)te^(-lambda t) dt)/( N_(0) ) = lambda int_(0)^(**) te^(-lambda t) dt`
`RARR tau = 1//lambda`
Relation of average life with HALF life :
`T_(1//2) = (I_(n) 2) /( lambda) = tau (I_(n) 2)`
`T_(1//2) = tau log_(e)^(2)`
Discussion
819.

A man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g/2 then the work done by the string on the block will be

Answer»

`-3mgd /2`
`+3mgd /2`
`-MGD /2`
`+mgd /2`

ANSWER :D
Discussion
820.

In the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t = 4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L = 2 xx 10^(-4)H, C = 5 mF, R = (In 2)/(10) Omega and emf of the battery = 1 V.

Answer»


Solution :CURRENT in `R` or `L` at any time is given by:
`I = (varepsilon)/(R )(1 - e^(-Rt//L)) rArr I = (1)/((In 2)//10) [1 - e^(-(t In 2)/(10xx2xx10^(-4)))]`
`rArr I = (10)/(In2) [1-e^(In 2^-((t)/(2xx10^(-3))))] rArr I = (10)/(In 2) [1-((1)/(2))^ ((t)/(2xx10^(-3)))]`
Now at `t = 4 ms`
`I = (10)/(In2)[1-((1)/(2))^((4xx10^(-3))/(2xx10^(-3)))] = (10)/(In 2)[ 1- (1)/(4)] = (15)/(2 In 2) A`
Now the switch is shifted between `A` and `C`. Just after SHIFTING the switch, current in INDUCTOR will be as calculated above. It can't change at once. Now due to this current, the capacitor will start charging. FREQUENCY of oscillation is given by :
`omega = (1)/(sqrt(LC)) = (1)/(sqrt(2 xx 10^(-4) xx 5 xx 10^(-3)))= 10^(3) rad//s`
To find maximum charge : `(Q^(2))/(2C) = (1)/(2) LI^(2)`
`rArr Q = (sqrt(LC))I = (10^(-3) xx 15)/(2 In 2) rArr Q = (7.5 xx 10^(-3))/(In 2) C`
Energy in the capacitor is half of total energy when charge on
capacitor is `q = (Q)/(sqrt(2))`
Charge on capacitor at any time
`q = Q sin omegat [ :' at t = 0, q = 0]`
`rArr (Q)/(sqrt(2)) = Q sin omega t rArr omegat = npi + (-1)^(n) (pi)/(4)`
(1) `rArr t = (n pi + (-1)^(n) pi//4)/(omega)`
Total time, `T = 4 ms + (n pi + (-1)^(n) pi//4)/(omega)`
Discussion
821.

Photo diodes are used to detect

Answer»

RADIO waves.
gamma rays.
IR rays.
optical signals.

Answer :A::C
Discussion
822.

An L-C-R series A.C. circuit is tuned to resonance. The impedance of the circuit is ……

Answer»

`[R^2 +(omegaL-1/(omegaC))^2]^(1/2)`
`[R^2+(omegaL)^2+(1/(omegaC))^2]^(1/2)`
`[R^2+(1/(omegaC)-omegaL)^2]^(1/2)`
R

Solution :When resonance occur, then `omegaL=1/(omegaC)`
`|Z|=sqrt(R^2+(omegaL-1/(omegaC))^2)=R`
Discussion
823.

Wavelength of light incident on a photo-sensitive surface is reduced from 3500 Å to 290 nm.The change in stopping potential is ……..(h=6.625xx10^(-34)Js)

Answer»

SOLUTION :`lambda=3500Å,lambda_(2)=290 nm.`
`h=6.625x10^(-34)` Js(given values)
`(1)/(2)mv_(max)^(2)=(HC)/(lambda)-phi=eV_(0)`
`therefore V_(01)e=(hc)/(lambda_(1))-phi`
`therefore V_(02)e=(hc)/(lambda_(2))-phi`
`therefore (V_(02)-V_(01))e=hc((1)/(lambda_(2))-(1)/(lambda_(1)))`
`therefore V_(02)-V_(01)=(hc)/(e)[(lambda_(1)-lambda_(2))/(lambda_(1)lambda_(2))]`
`=(6.625xx10^(-34)xx3xx10^(8))/(1.6xx10^(10^(-19)))`
`[(3.5xx10^(-7)-2.9xx10^(-7))/(3.5xx10^(-7)xx2.9xx10^(-7))]`
`=12.42[(0.6)/(3.5xx2.9)]`
Discussion
824.

A frustum is cut from a right circular cone. The two circular faces have radii R and 2R and their centers are at O_(1) and O_(2) respectively. Height of the frustum is h=3R. When a point charge Q is placed at O_(1), the flux of electric field through the circular face of radius 2R is phi_(1) and when the charge Q is placed at O_(2), the flux through the other circular face is phi_(2). find the ratio (ph_(1))/(phi_(2))

Answer»


ANSWER :`((SQRT(13)-3)/(sqrt(10)-3))sqrt((10)/(13))`.
Discussion
825.

Two coils P and Q are at fixed position. When coil P has no current in coil Q increases at the rate of 5As^(-1), the e.m.f. in coil P is 20 mV. What is the mutual inductance? When the coil Q has no current and coil P has a current of 3A, what is the flux linkage in coil Q?

Answer»

Solution :`varepsilon_(1)=M(di_(2))/(DT),""varepsilon_(1)=20xx10^(-3)V, (di_(2))/(dt)=5As^(-1)`
`M=(varepsilon_(1))/(((di_(2))/(dt)))=(20xx10^(-3))/(5)=4mH`
Flux linkage in coil `Q=N_(Q).phi_(QP)=M.i_(1)=4XX10^(-3)xx3=12xx10^(-3)` weber
Discussion
826.

If the forward bias voltage a p - n junction diode is changed form 0.7 V to 2.2 V , the forward current changes by 1.5 mA, the forward resistance of diode is :

Answer»

`100 Omega`
`500 Omega`
`1000 Omega`
`500A`

Solution :`r_f=(DELTAV)/(DeltaI)=(2.2-0.7)/(1.5xx10^(-3))=1000Å`
Discussion
827.

Of the following which is preferred modulation scheme for digital communication.

Answer»

PCM
PAM
PPM
PTM

Solution :Pulse CODE Modulation is PREFERRED modulation SCHEME for DIGITAL COMMUNICATION.
Discussion
828.

If the circuit is connected to a high frequencysupply (240 V, 10 kHz). Hence, explain the statement that at very high frequency, an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a dc circuitafter the steady state?

Answer»

Solution :`omega = (E_0)/(SQRT(R^2 + (2PI v L)^2) )= (240sqrt2)/(sqrt(100^2 + (2pi xx 10^4 xx 0.5)^2)) = 0.11A`
` tan phi = (2pi vL)/( R) = (2pi xx 10^4 xx 0.5)/(100) = 100 pi`
`phi` is close to `pi/2` , then time lag ` = (2pi)/(omega) .pi/2. (qv)/(360) = 0.25 xx 10^(-4) s `
`I_0` being very SMALL we can conclude that at high frequencies , an inductor BEHAVES as an open circuit .
In dc circuit , ` v = 0` . so inductor acts as a conductor .
Discussion
829.

The radius of curvature of eachface of biconcave lens, made of glass of refractive index 1.5 is 30 cm. Calculate the focal length of the lens in air.

Answer»

Solution :Here `n = 1.5 , R_(1) = - 30 CM , R_(2) = 3 cm`
Using len.s maker.s formula,
`(1)/(F) = (n-1)((1)/(R_(1))-(1)/(R_(2)))`
`=(1.5-1)[(1)/(-30)-(1)/(30)]=0.5xx((-2)/(30))`
`(1)/(f) = - (1)/(30)`
f = - 30 cm
Discussion
830.

The atmospheric pressure is measured with a Fortin's barometer having a vernier scale. 20 divisions of the vernier scale coincide with 19 main scale divisions. Each division of the main scale is equal to 0.5 mm. Which of the following correctly expresses the atmospheric pressure ?

Answer»

71.0000 CM of HG
71.000 сm of Hg
71.00 cm of Hg
71.0 cm of Hg

Solution :Least count of VERNIER scale `=(0.5)/(20)` mm=0.0025 cm
It has significant digits UPTO four place of decimal. In OBSERVATION 71.0000 cm of Hg also, there are four significant digits after the decimal point.
Discussion
831.

One end of a cylindrical glass rod (mu = 1.5) is given the shape of a concave refracting surface of radius 10cm. An air bubble is situated in the glass rod at a point on its axis such that it appears to be at distance 10 cm from the surface and inside glass when seen from the other medium. Find the actual location of air bubble.

Answer»

Solution :Using ` (mu_2 )/(v ) - (mu_1)/(U) =(mu_2 -mu_1)/(R )`

` mu_1= 1.5 ,mu_2 =1`
`v=-10CM, R= +10cm`
` therefore -(1)/(10) - (1.5 )/(u ) = (1-1.5 )/(10) =-(1)/(20)`
`(1.5 )/(u ) =-(1)/(10 )+(1)/(20) =-(1)/(20)`
` thereforeu=-30 CM`
Hence the air BUBBLE is actually located at a distance 30cm from the surface and INSIDE glass.
Discussion
832.

Degree of modulation

Answer»

can take any value
should be LESS than 100%
should EXCEED 100%
none of the these

ANSWER :B
Discussion
833.

(A): In forward bias, zener diode acts like an ordinary P-n junction diode. (R): Zener diode is used as a voltage regulator.

Answer»

Both 'A' and 'R' are TRUE and 'R' is the CORRECT EXPLANATION of 'A'
Both 'A' and 'R' are true and 'R' is not the correct explanation of 'A'
'A' is true and 'R' is false
'A' is false and 'R' is true

ANSWER :B
Discussion
834.

p-side of semiconductor is earthing and -2V potential applied at n-side so in diode …..

Answer»

CURRENT is FLOWING.
it is BREAKDOWN.
current is not flowing.
partial current is flowing.

Solution :current is flowing.

`therefore` On forming forward BIAS connection, current is flowing.
Discussion
835.

State the importance of coherent sources in the phenomenon of interference. In Young's double-slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence, deduce the expression for the fringe width. How does the fringe width get affected, if the entire experimental apparatus of Young's is immersed in water ?

Answer»

Solution :Coherent sources of light are required in order to obtain a SUSTAINED nterference pattern on a screen which does not CHANGE with time.
For conditions for constructive and destructive interference in Young.s double-slit experiment and EXPRESSION for the fringe width.
Let fringe width of interference pattern in AIR be `beta` where `beta=(lamdaD)/(d)`.
If whole APPARATUS of Young is immersed in water of refractive index `.n_(w).` the wavelength of light changes from `lamda` to `lamda_(omega)`, such that `(lamda)/(lamda_(w))=n_(w) or lamda_(w)=(lamda)/(n_(w))`
`therefore` Net fringe width of interference pattern in water `beta_(w)=(lamda_(w).D)/(d)=(lamdaD)/(n_(w).d)=(beta)/(n_(w))`.
Discussion
836.

Ravi is a student of mechanical engineering studying in one of the engineering colleges. The other day he saw an old man who suddenly collapsed as he walked out of the house in his neighbourhood. Ravi the emergency ward of the hospital. On getting the medical aid, the old man soon goy recovered. He did not forget to thank Ravi for the timely help he rendered. He was wondering that in his times to get the telephone connection. One had to wait for years whereas these days it takes no time to get the connection. Ravi told him it was all because of the technological progress/deveolpement due to which the simple phenomenon in physics could be easily used. Answer the following questions based on the above : (a) To which phenomenon in physics was Ravi referring to, which made the land line links so easily accessible? (b) What are the essential conditions required to observe this phenomenon ? (c) Write two values displayed by Ravi and the old man in this episode.

Answer»

Solution :(a) (i) Total internal reflection.
(b)(i) Light should go from denser mdeium to rarer medium.
(II) Angle of incidence should be greaterf than critical angle.
(c) Values displayed by Ravi (i) Helpful (helping ATTITUDE),(ii) KNOWS how to use modern TECHNOLOGY. By old man : (i) Thankful , (ii) Surprised to see changes in technology.
Discussion
837.

Half of an infinitelylong straightcurrent-carryingsolenoid is filledwith magneticsubstanceas shown in Fig. Draw the appoximater plotsof magnetic inductionB, strengthHand magnetizationJ on theaxis as functions of x.

Answer»

Solution :We canobtainthe form of the curves, requiredhere,by quanlitative arguments.
From`oint vec(H).d. vec(l) = I`
we GET `H(x gt gt o) = H(x lt lt o) = nl`
Then`B(x gt gt 0) = MU mu_(0) NI`
`B(x lt lt o) = mu_(0) nI`
Also, `B (x lt 0) = mu_(0) H (x lt o)`
`J(x lt 0) = 0`
`B` is CONTINOUS at `x = 0`, `H` is not. These give the requiredcurvesas shwon in the anser sheet.
Discussion
838.

The temperature coefficient of resistance of a wire is 0.00125 per ""^(@)C. At 300 K, its resistance is 1Omega. The resistance of the wire will be 2Omega at

Answer»

1154 K
1100 L
1400 K
1127 K

Answer :D
Discussion
839.

Consider a wire of length 4m and cross - sectional area 1mm^(2) carrying a current of 2A. If each cubic metre of the material contains 10^(29) free electrons, find the average time taken by an electron to cross the length of the wire.

Answer»

SOLUTION :`RARR v_(d)=(i)/(nAe)=(2)/(10^(29)xx10^(-6)xx1.6xx10^(-19))ms^(-1)`
`=12.5xx10^(-4)ms^(-1)`
`rArr"Average TIME takne by an electron to cross the LENGTHOF wire"`
`t=(1)/(v_(d))=(4)/(1.25xx10^(-4))s=3.2xx10^(4)s`
Discussion
840.

Assertion (A) : A compass needle when placed on the magnetic north pole of the earth may lie in any direction. Reason (R) : The earth has only vertical component of its magnetic field at the north pole.

Answer»

If both ASSERTION and reason are TRUE and the reason is the CORRECT explanation of the assertion
If both assertion and reason are true but reason is not the correct explanation of the assertion
if assertion is true but reason is FALSE.
If the assertion is false but reason is true.

Solution :If both assertion and reason are true but reason is not the correct explanation of the assertion
Discussion
841.

A hydrogen atom emits a photon of energy 12.1 eV. Its orbital angular momentum changes by triangleL. Then triangleL equals :

Answer»

`1.05 XX 10^(-34)JS`
`2.11 xx 10^(-34)Js`
`3.16 xx 10^(-34)Js`
`4.22 xx 10^(-34)Js`

Solution :`E=-13.6ev, E_(2)=-3.4ev, E_(4)=-0.85ev`
`RARR E_(3)-E_(1)=12.1ev ("transition for n=3 to n=1")`
`triangle L=(3-1) (LAMBDA)/(2PI) =(lambda)/(pi) =2.11 xx 10^(-34)J_(s)`
Discussion
842.

An equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is mu_w=4//3.

Answer»


ANSWER :40 CM
Discussion
843.

The optical path of a monochromatic ray of light is the same if it travels 2 cm through glass or 2.25 cm through water. If the refractive index of water is 4/3, then the velocity of light in glass will be :

Answer»

`2.25 XX 10^8 m//s`
`1.5 xx 10^8 m//s`
`2 xx 10^8 m//s`
`1.75 xx 10^8 m//s`

ANSWER :C
Discussion
844.

For a wavelength of light lambda and scattering object of size 'a', all wavelength are scattered nearly equally , if

Answer»

`a = LAMBDA`
`a gt gt lambda`
`a LT lt lambda`
`a GE lambda`

Solution :For ` a gt gt lambda`, the SCATTERING power is not selective.
Discussion
845.

The velocity acquired by a charged particle of mass m and charge Q accelerated from rest by a potential of V is

Answer»

a. `(QV)/(m)`
B. `SQRT((m)/(QV))`
C. `sqrt(MQV)`
d. `sqrt((2QV))/(m)`
Discussion
846.

A solenoid of length 50cm with 20 turns per centimetre and area of cross-section 40cm^2completely surrounds another coaxial solenoid of the same length, area of cross-section 25cm^2with 25 turns per centimetre. Calculate the mutual inductance of the system.

Answer»

Solution :`L= 50 CM = 1/2 m`
`N_1 = 20 XX 50 = 1000, A_1 = 40 xx 10^(-4) m^2`
`N_2 = 25 xx 50 = 1250 , A_2 = 25 xx 10^(-4) m^2`
`M = (mu_0 N_1N_2A_2)/(l)`
` = (4pi xx 10^(-7) xx 1000 xx 1250 xx 25 xx 10^(-4) )/(1//2) H`
` = 7.9 xx 10^(-3) H = 7.9 mH`
Discussion
847.

The part of a transistor, which is heavily doped to produce a large number of majority carriers is called

Answer»

EMITTER
base
collector
any ONE out of emitter, base and collector

Solution :Emitter of a transistor is heavily doped so as to act as SOURCE of majority charge CARRIERS.
Discussion
848.

(a) Using Gauss law, derive expression for electric field due to a spherical shell a uniform charge distribution sigma and radius R at a point lying at a distance r from the centre of shell, such that (i) O lt r lt R, and (ii) r gt R. (b) An electric field is uniform and acts along +x direction in the region of positive x. It is also uniofrm with the same magnitude but acts in -x direction in the region of negative x. The value of the fleld is E= 200 N/C for xgt 0 and E=-200 N//C" for "x lt 0. A right circular cylinder of length 20 cm and radius 5 cm has its centre at the origin and its axis along the x-axis so that one flat face is at x =+ 10 cm and the other is at x=-10 cm. Find : (i) The net outward flux through the cylinder. (ii) The net change present inside the cylinder.

Answer»

Solution :(a) (i) Consider a hollow charged conducting sphere of radius R and having charge Q. To find electric field at a point P inside the shell, consider a sphere through point P and having centre O, i.e, r= OP `("where "O lt r lt R)` as the GAUSSIAN surface.
The electric flux through the Gaussian surface `phi_(E)=oint vecE. hatn ds=E 4pi r^(2) ....(i)`
According to Gauss theorem, total electric flux should be
`phi_(E)=(1)/(epsi_(0)) ("charged enclosed")=0`
Thus, `phi_(E)=E.4pi r^(2)=0`
[Since the Gaussian surface is not enclosing any charge) Thus,`phi_(E)=E.4 pi r^(2)=0`
`rArr E=0`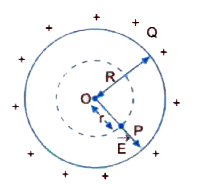

(ii) To find electric field intensity at a point Poutside the shell situated at a distance `r (r gt R)` from the centre of shell, consider a sphere of radius r as the Gaussian surface. All points on this surface are equivalent relative to given charged shell and, thus, electric field E at all points of Gaussian surface has same magnitude E and `vecE` and i are parallel to each other.
Total electric flux over the Gaussian surface
`phi_(E)=oint vecE. hatn dx=E.4pir^(2) ......(i)`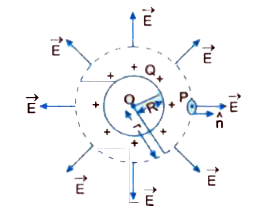

According to Gauss.s theorem, `phi_(E)=1/in_(0) ("charged enclosed")=Q/(in_(0))` ........(ii)
Comparing (i) and (ii), we get
`E.4pi r^(2)=Q/in_(0) or E=Q/(4pi in_(0) r^(2))`
If surface charge DENSITY of shell be `sigma" then Q"=4piR^(2), sigma` and therefore
`E=(4piR^(2) sigma)/(4pi in_(0) r^(2))=(sigmaR^(2))/(in r^(2))`
(B) The situation is shown in the given figure. Here,
`E=200 NC^(-1)` length of cylinder l=20cm, 0.2m, radius of cylinder R=5cm, =0.05m
(i) As shown in figure the net OUTWARD electric flux is along x-axis and HASA value
`phi_(E)=2E triangles`
`=2EpiR^(2)`
`=2 xx 200 xx 3.14 xx (0.05)^(2)`
`=3.14 Nm^(2) C^(-1)`
(ii) As per Gauss law, net charge present inside the cylinder
`q=in_(0) xx phi_(E)=(8.854 xx 10^(-12))xx 3.14 =2.78 xx 10^(-11) C`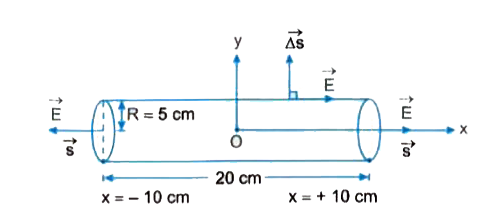
Discussion
849.

The refractive index of the material of a concave lens is nv It is immersed in a medium of refractive index n2. A parallel beam of light is incident on the lens. Trace the path of emergent rays

Answer»

SOLUTION :
Discussion
850.

When is the p-n junction called reverse bias and explain the change in p-n junction from this type of connection.

Answer»

SOLUTION :When and external voltage (V) is applied across the diode such that n-side is positive and p-side is negative it is said to be reverse biased. This is shown in figure.

Diagram (b) for the circuit is as follows :

The applied voltage mostly drops across the depletion region according to figure (a).
The direction of applied voltage `V_(0)` is same as the direction of barrier potential V. As a result, the barrier height increases and the depletion region widens DUE to the change in the electric field.

The effective barrier height under reverse bias is `V+V_(0)`.
In figure (c ), the battery is not connected to p-n junction, potential barrier `V_(0)` is shown as 1 and when voltage of the external battery is applied, its effective potential barrier `V_(0)+V` is shown as 2.
This suppresses the flow of electrons from `n to p` and holes from `p to n` due to effectivedepletion barrier potential means current are disputed due to majority CHARGE carriers hence DIFFUSION current is not obtained.
Although some MINORITY charge carriers pass through the junction due to the high voltage applied by external battery hole in n-region and electron in p-region and current flow in reverse direction is called reverse current. However, for largereverse voltage, the increase in reverse current shows less.
Reverse current does nto depend only on the applied voltage. The current is not limited by the magnitude of the applied voltage but is limited due to the concentration of the minority carrier on either side of junction.
Some voltage is also sufficient to across the junction for minority carriers.
The reverse bias voltagevaries from about 10 V to 15 V.
Here current obtained in the order of microampere `(muA)`.
Discussion