Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 38851. |
The working principle in atom bomb is |
|
Answer» under-critical CHAIN REACTION |
|
| 38852. |
Alnico is a alloy of which metals ? |
| Answer» Solution :IRON, ALUMINIUM, Nickel, COBALT, COPPER | |
| 38853. |
The photo current in an experiment on photoelectrie effect increases if |
|
Answer» the INTENSITY of the SOURCE is increased |
|
| 38854. |
If R is the range and T is the time of flight of a projectile then the angle of projection is given by : |
|
Answer» `TANTHETA=(G t^(2))/(R)` `T^(2)=(4u^(2)sin^(2)THETA)/g:. T^(@)/R=(2sintheta)/(costheta)xx1/g` or `tantheta=(g t^(2))/(2R)` |
|
| 38855. |
A rocket in a fireworks display explodes high in the air. The sound spreads out uniformly in all directions. The intensity of the sound is 2.0 xx 10 W//m^2at a distance of 120 m from the explosion. Find the distance from the source at which the intensity is 0.80 xx 10^(-6)W//m^2 . |
|
Answer» 690 m |
|
| 38856. |
How does focal length of a lens change when red light is replaced by violet light? |
| Answer» SOLUTION :`1/f =(mu_(21) - 1) ((1)/(R_1) - (1)/(R_2) ). " As" mu_b GT mu_r` | |
| 38857. |
Two particles of equal mass 'm' go around a circle of radius 'R' under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is : |
|
Answer» `sqrt((Gm)/(4R))`  `(Gm.m)/((R+R)^(2))=m.R.omega^(2)` or `omega^(2)=(Gm)/(4R^(3))` or `omega=sqrt((Gm)/(4R^(3))` Now, `v=Romega=Rsqrt((Gm)/(4R^(3)))=sqrt((Gm)/(4R))` |
|
| 38858. |
(a) In the arrangmenet shown in the figure the frictional coefficient between the traingular wedge and floor is mu = 1//sqrt(3). The frictional force is sufficient to keep the system in equilibrium. Find how much the normal reaction between the wedge and floor is displaced from the centre of mass of wedge. All other surface are frictionless. Assume masses of both the bodies same and equal to m. Radius of sphere =R, length of side of triangular wedge d = 3 sqrt( 3) R . ( b) If the surface of contact between the floor & the wedge also becomes frictionless, the find the speed of both bodies when sphere hits the ground. Initial height of centre of mass of sphere = 2R as shown. |
|
Answer» |
|
| 38859. |
Five identical capacitor plates each of area A, are arranged such that adjacent plates are at d distance apart. Plates are connected to a source of e.m.f epsilonas shown in fig. Match the following: {:("COLUMN - I ","COLUMN - II"),("a) Charge on plate 1", "P) " -2epsilon_(0)AV//d),("b) Charge on plate4","q)" +epsilon_(0)AV//d),("c) Potential difference between plates 2 and 3","r) zero"),("d) Potential difference between plates 1 and","s)" V):} |
|
Answer» |
|
| 38860. |
A circular copper ring of radius r, placed in vacuum, has a charge q on it. Find out the electric fields For what value of x would the electric field be maximum? |
|
Answer» Solution :For E to be MAXIMUM, `(DE)/(dx)=0` Now, `(dE)/(dx)=q/(4piepsilon_(0))cdotd/(dx)[x(R^(2)+x^(2))^(-3//2)]` `=q/(4piepsilon_(0))[1cdot(r^(2)+x^(2))^(-3//2)+xcdot(-3/2)cdot(r^(2)+x^(2)^(-5//2)cdot2x]` `=q/(4piepsilon_(0))(r^(2)+x^(2))^(-5//2)[(r^(2)+x^(2))-3x^(2)]` `=q/(4piepsilon_(0))(r^(2)+x^(2))^(-5//2)(r^(2)-2x^(2))` For maximum E, `(dE)/(dx)=0` or `r^(2)-2x^(2)=0` or, `x=pmr/(sqrt2)` The `'pm'` sign implies that the electric FIELD on the axis will be maximum at a distance `r/(sqrt2)` on either side of the RING. |
|
| 38861. |
The hysterisis curve generally studies in case of _____ substances. |
| Answer» SOLUTION :FERROMAGNETIC | |
| 38862. |
Aray of light travelling in water is incident on its surfac open to air. The angle of incident is theta, which is less than the critical angle. Then there will be : |
|
Answer» only a REFLECTED ray and no refracted ray  The angle between reflected and refracted ray is `LT(180^(@) - 2theta)`. |
|
| 38863. |
A series R-L-C circuit has R = 100 Ohm. L = 0.2 mH and C = (1)/(2) mu F. The applied voltage V = 20 sin omega t. When the current lags the applied voltage by 45^(@), the equation of the current is |
|
Answer» `0.2 SIN (OMEGA t + TAN^(-1) 0.3)` |
|
| 38864. |
The mean lives of a radioactive subtance are 1620 and 405 years for alpha -emission and beta -emission simultaneously, the time after which three fourth of sample will decay is nearly (x)/(2)xx(10)^(2) year, where x = ______ [take log_(10)^(4)=0.603 ] |
|
Answer» 449.94 YEARS |
|
| 38865. |
Proton with kinetic energy T=1.0MeV striking a lithium target induce a nuclear reaction p+Li^(7)rarr 2He^(4). Find the kinetic energy of each alpha-particles and the angle of their divergence provided their motion directions are symmertical with respect to that of incoming protons. |
|
Answer» Solution :The `Q`value of the reaction `Li^(7)(p,ALPHA)He^(4)` is `Q=(Delta_(Li)^(7)+DeltaH-2Delta_(He)^(4))C^(2)` `=(0.01601+0.00783-0.00520)am uxxc^(2)` `=0.01864 am uxxc^(2)= 17.35MeV` Since the direction of `He^(4)` nuclei is symmertical, their momenta must also be equal. Let `T` to be `K.E` of each `He^(4)`. Then `P_(p)=2sqrt(2m_(He)T) `cos`(theta)/(2)` `(P_(p)` is the number of proton). Also `(p_(p)^(2))/(2m_(p))+Q= 2T=T_(P)+Q` Hence `T_(p)+Q=2(P_(p)^(2)"SEC"^(2)(theta)/(2))/(8m_(He))` `T_(p)(m_(p))/(2m_(He))"sec"^(2)(theta)/(2)` Hence `"cos"(theta)/(2)=sqrt((m_(p))/(2m_(He))(T_(p))/(T_(p)+Q))` Substitution gives `theta= 170.53^(@)` Also `T=(1)/(2)(T_(p)+Q)= 9.18MeV` 
|
|
| 38866. |
State the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T_(1/2). Depict in the plot the number of undecayed nuclei at (i) t= T_(1/2) and (ii) t= 5T_(1/2). |
|
Answer» Solution :According to law of radioactive decay, the rate of decay of a radioactive sample at a given instant is directly proportional to the actual NUMBER of radioactive nuclei of that element present in the given sample at that instant of time. Mathematically, `R(t)=(-dN)/(DT)=lambdaN` where `lambda` is a constant, known as the disintegration or decay constant, of the given sample. From radioactive decay law it is found that `N= N_(0)e^(-lambdat)` and `R=R_(0)e^(-lambdat)` Thus, number of nuclei of a radioactive sample (and consequently the ACTIVITY of the sample too) decreases exponentially with time. A graph to illustrate radioactive decay has been shown in Fig. 13.08.  From the graph, it is clear that number of undecayed nuclei at (i) `t=3T_(1/2)` is `N_(0)/8` and (ii) `t=5T_(1/2)` is `N_(0)/32` |
|
| 38867. |
Which experiment first demonstrated the type and properties of interference ? |
| Answer» SOLUTION :THOMAS Young.s DOUBLE SLIT | |
| 38868. |
Which is the vital link that ensures continuity of species between organisms of one generation and the next? |
|
Answer» SEXUAL reproduction |
|
| 38869. |
A ring of radius 3 m has charge density lambda. Electric potential at 4 m from its centre on its axis is ____ [k=(1)/(4pi epsilon_(0))] |
|
Answer» `(2)/(5) pi K lambda` |
|
| 38870. |
A charged oil drop is suspended in a uniform field of 3xx10^(4) V/m so that it neither falls nor rises. The charge on drop will be (Take mass of charge =9.9xx10^(-10) 10^(-15)kg and g=10m//s^(2)). |
|
Answer» `2.3xx10^(-18)C` `:.Q=(mg)/(E)=(9.9xx10^(-15)xx10)/(3xx10^(4))` `:.q=3.3xx10^(-18)C` |
|
| 38871. |
A wave y_i =0.3 cos (0.2x-40t) is travelling along a string toward a boundary at x = 0. Write expressions for the reflected waves if The string has a free end at x=0. Assume SI units. |
| Answer» SOLUTION :`y(X,t)= 0.3 COS (2.0 + 40 t)` SI units | |
| 38872. |
A wave y_i =0.3 cos (0.2x-40t) is travelling along a string toward a boundary at x = 0. Write expressions for the reflected waves if The string has a fixed end at x = 0. |
| Answer» SOLUTION :`y (X,t) = 0.3 COS (2.0 x + 40 t +PI)` | |
| 38873. |
Two paper screens A and B are separated by a distance of 100 m. A bullet pierces A and then B. The hole in Bis 10 cm below the hole in A. of the bullet is travelling horizontally at the time of hilling the screen A, calculate the velocity of the buller when it hits the screen A. Neglect the resistance of paper and air. |
Answer» SOLUTION :The SITUATION in SHOWN in fig. 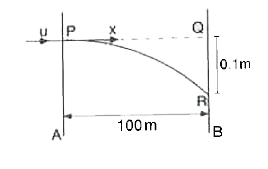 `d=u sqrt((2(h_(1)-h_(2)))/(g))` `100=u sqrt((2xx0.1)/(9.8))` `u=700 m//s` |
|
| 38874. |
There are n similar conductors each of resistance R. The resultant resistance comes due to be x when connected in parallel. If they are connected in series, the resistance comes out to be: |
|
Answer» `x/n^2` |
|
| 38875. |
The magnetic moment of the loop shown in the adjacent figure is : ( length of each side is a ) |
|
Answer» `-3A^(2)I HAT(k)` |
|
| 38876. |
Eleven equal wires each of resistance 2 Omega form the edges of an incomplete cube. Find the total resistance from one end of vacant edge to the other end of the same edge. |
Answer» Solution :Let ABCDFGHK be the open cube formed by joiningeleven EQUAL wires each of resistance `2 Omega` 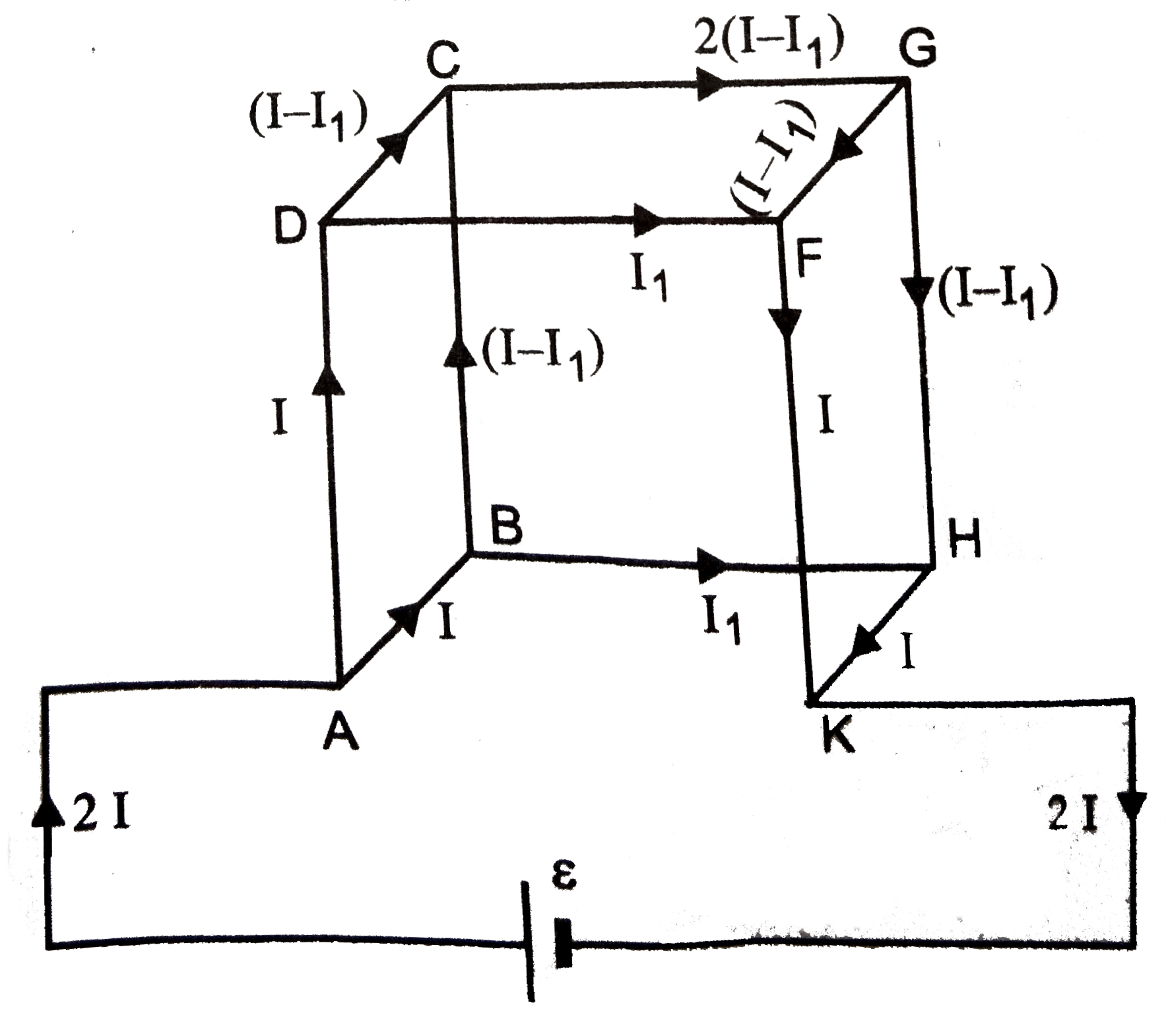 Let the current from the cell of emf `epsilon` enter the cube at corner A and after passing through all the wiresleave at K, the other end of the open edge of the cube. For the sake of convenience, let us suppose that the total current is 2I. At A, this current is divided into two parts : I along AB and I AD. This is beacuse the resistances of the two paths are equal. At the points B and D, each part of current is further divided into two uneqaul parts. The DISTRIBUTION of current in the various arms of skeleton cube is shown according to Kirchhoff's first rule. The current leaving the cube at K is again 2 I. Let R be the equivalent resistance of skeleton cube between edges A and K. From Ohm's LAW, `epsilon = 2 I R` Applying Kirchhoff's second rule to mesh `epsilon` ABHK`epsilon` , we have `epsilon = 2 xx I + 2xx I_(1) + 2 xx I` or `epsilon= 4 I+2I_(1)` Applying Kirchhoff's Second rule to mesh of DFGCD, we have `2 I_(1) - 2 (I -I_(1)) -2 xx 2 (I - I_(1)) - 2 (I-I_(1))=0` `2 I_(1) - 2I + 2 I_(1) - 4 I + 4 I_(1) + 2 I + 2I_(1)=0` or `10_(1)-8I=0 or 8 I = 10 I_(1)` or `I_(1) = 8/10 I = 4/5 I` From (ii) and (iii), `epsilon = 4 I + 2 ((4)/(5)I) = (28 I)/5` From (i) and (iv), `2 Ir = (28I)/5 or R = 28/(5xx2)= 2.8 Omega` |
|
| 38877. |
{:("List-I","List-2"),((a)"Same negative dimensions of mass ",(e)"Pressure, Rydberg constant "),((b)"Same negative dimensions of length", (f) "Magnetic induction field, potential"),((c)"Same dimensionof time " ,(g) "Capacity, Universal gravitational constant "),((d) "Same dimensions ofcurrent" ,(h)"Energy density, Surface tension"):} |
|
Answer» a - G`""` B- e `""`c -H `""` d-F |
|
| 38878. |
A radioactive nucleus X decays to nucleus Y whichfurther decays to a stable nucleus Z as given belowX overset(lamda_(x) = 0 , 1 sec^(-1))rarr Y overset(lamday=(1)/30sec^(-1))rarrZ (stable). Initially the sample contains nuclei of X only and its population is N_(0) = 10^(20) . Further the population of Y as function of time is given by N_(Y)(t) = (N_(0)lamdaX)/(lamda_(X) - lamda_(Y)) (e^(-lamda)y^(t) -e^(-lamda)x^(t)) (a) If N_(X),N_(Y) and N_(Z) represent population of X, Y and Z respectively at any instant of time t . Find (dN_Y)/(dt) (b) Find the time at which population of Y is maximum (c) Find the population of X at instant when N_Y is maximum |
|
Answer» |
|
| 38879. |
The amplitudeof polarised light transmitted through polariseris A . The amplitude of unpolarised light in incideationon it is |
|
Answer» `A/2` |
|
| 38880. |
A neutron of kinetic energy 65eV collides inelasticallywith a single ionized helium atom at rest.It is scattered at an angle of 90^(@) with respect of its original direction. (i) Find the allowed values of the energy of the neutron & that of the atom after collision. (ii) If the atom gets de-excited subsequently by emitting radiation, find the frequencies of the emitted radiation. (Given : Mass of the atom = 4 xx( mass of neutron ) , ionization energy of H atom = 13.6 eV ) |
|
Answer» |
|
| 38881. |
Draw the diagram of a light ray travelling from rarer to denser medium |
| Answer» SOLUTION :`n_2>n_1` | |
| 38882. |
The ionisation energy of an electron in the ground state of helium atom is 24.6V. The energy required to remove both the electron is : |
|
Answer» 51.8eV Energy REQUIRED to remove 2 electrons from `He^(2+)` `=Z^(2) (13.6)EV =(2)^(2) (13.6) =54.4eV` So, TOTAL energy required =24.6+54.4=79eV |
|
| 38883. |
A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Omega Determine the equivalent resistance of the network and the current along each edge of the cube. |
|
Answer» Solution :Above cubical network ls shown as per the statement, where each of 12 identical sides, is a resistor of resistance R = 1 `Omega`. We have to find equivalent resistance of this network between its diagonally opposite points, SAY between points A and G in above figure. For this purpose, connect a battery across these two points. Now, current I starting from positive terminal of battery reaches point A, after which it is offered three branches AB, AD and AE and so it is divided into three parts. Here, minimum resistance offered to each of these three parts to reach negative terminal of battery is same and so all of these three parts are equal. Hence, each part wouJd be I/3. Thus, current arriving at points E, D and B are all I/3. These all currents are further divided into two parts as all of them are further offered two branches after points B, D and E. Here, minimum resistance offered to each of these two parts to reach negative terminal of battery is same and so each 1/3 amount of current gets divided into two equal parts after coming to points B, D and E. Hence, currents passing through BC and BF, DC and DH, EF and EH are all `((I)/(3))/(2) = (1)/(6)` . Now, at each of the junctions C, F and H, two cu.rrents each of amount 1/6 add up to give 1/3 amount of current, which FLOW in the branches CG, FG and HG respectively. These three cu.rrents each of amount 1/3 associate at exit point G to give total current I which is equal to current at the entry point A of given cubical network.. Now, applying KVL (Kirchhoff.s Voltage LAW) in the direction of current along the closed path AEHGJKA we get, - `((I)/(3)) (R) - ((I)/(6)) (R) - ((I)/(3)) (R) = - epsilon ` `thereforeepsilon = (IR)/(3) + (IR)/(6) + (IR)/(3) ` `therefore epsilon = (5 IR)/(6) "" `... (1) Now, if equivalent resistance of given cubical network between its diagonally opposite end points is `R_(eq)`, then `R_(eq) = (epsilon)/(I) = (5R)/(6)` [ From equation (1) ] ... (2) Here R = 1 `Omega` and so : `R_(eq) = (5)/(6) Omega` From equation (1) , `10 = (5I xx 1)/(6)` `therefore I = 12 A ` Current through branches AB, AD, AE, CG, FG, HG is , `(I)/(3) = (12)/(3) = 4` A Current through branches BC, BF, DC, DH, EF, EHis , `(I)/(6) = (12)/(6) = 2 ` A |
|
| 38884. |
Which of the following wiring diagrams could be used to experimentally determine R using ohm.s law? Assume an ideal voltmeter and an ideal ammeter. |
|
Answer»
|
|
| 38885. |
If 0.1muCtotal charge is uniformly distributed over long straight wire of having 10^(-5) cm^(-1)linear charge density, then length of the wire would be........... |
|
Answer» Solution :`LAMBDA = Q/L` `therefore L =Q/lambda = (10^(-7))/10^(-5) = 10^(-2)m = 1cm` |
|
| 38886. |
The work function of caesium metal is 2.14 ev. When light of frequency 6 xx10^(14)Hz is incident on the metal surface, photoemission of electrons occurs. What is the (a) maximum kinetic energy of the emitted electrons, (b) Stopping potential, and (c) maximum speed of the emitted photoelectrons? |
|
Answer» Solution :(a) `0.34eV=0.54xx10^(-19)J` (B) 0.34 V (c) 344 km/s |
|
| 38887. |
A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v_0 and forms an angle alpha with the horizontal. |
|
Answer» Solution :The force with which the cylinder wall ACTS on the particle will PROVIDE centripetal force necessary for the motion of the particle, and since there is no acceleration acting in the horizontal direction, horizontal component of the velocity will remain constant throughout the motion. So `v_x=v_0 cos ALPHA` Using, `F_n=mw_n`, for the particle of mass `m`, `N=(mv_x^2)/(R)=(mv_0^2cos^2alpha)/(R)` which is the REQUIRED normal force. 
|
|
| 38888. |
What's band width? |
| Answer» SOLUTION :Its DIFFERENCE between the upper and lower frequency limits of the SIGNAL or equipment operation VARY. | |
| 38889. |
The number of solution(s) of the trigonometric equation sec^2x+cosec^2x-sin2x-3=0, in [0, 4pi], is |
|
Answer» 2 `1+tan^2x+1 + cot^2x=1+sin2x+2` `2+tan^2x+cot^2x =(sin x+cosx)^2 +2` Range of LHS is `[4,oo]` Range of RHS is [2,4] So SOLUTIONWILL exist when sin2x=1 and tanx=cotx= `pm`1 `2x=x/2(4n+1)` `x=pi/4,(5pi)/4,(9pi)/4,(13pi)/4` at these x the VALUE of tan x = cot x =1 so number of solution = 4 |
|
| 38890. |
In the arrangement shown infigure z_(1) and z_(2) are twoscreen . Line PO is the bisectorline of S_(1)S_(2)and S_(3)S_(4) is removed, resulatnt at O dueto slitsS_(1) and S_(2)is l Nowz_(1) placed .For different values of y givenin column -I match the resultant intensity at Ogiven in Column- II , {:("Column I","Column -II"),(y=(Dlambda)/(6d),3l),(y=(Dlambda)/(6d),zero),(y-(Dlambda)/(4d),l),(y=(Dlambda)/(3d),"None ofthese"):} |
|
Answer» |
|
| 38891. |
The focal length of a convex lens is f. When it is divided in two parts by a plane parallel to the principal axis, focal length of each part will be _____ |
|
Answer» f |
|
| 38892. |
Sound waves are passing through two routes- one in straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown in the figure. If the velocity of sound waves in the pipe is y, then frequencies of resultant waves of maximum amplitude will be integral multiples of |
|
Answer» `v /(r(pi-2))`  The PATH difference between TWO intefering waves is, `Deltax = PIR - 2r =r(pi-2)` For maximum AMPLITUDE, `Deltax = nlambda` `r(pi-2) = nlambda` or `LAMBDA =(r(n-2))/n` Frequency, `u=v/lambda =n[(v)/(r(pi-2))]` |
|
| 38893. |
Two plane mirrors are placed parallel to each other at a distance L apart. A point object O placed between them, at a distance L//3 from obe mirror. Both mirros form multiple image. The distancebetween any two images cannot be |
| Answer» Solution :N//A | |
| 38894. |
What is the future compared to in the poem? |
|
Answer» A movie |
|
| 38895. |
A dip circle is set in position after leveling and the dip is found to be alpha . Then it is rotated through 45^(@) away from the magnetic meridian from this position and the dip is found to be beta Show that true dip is given by cot^(2)delta=2(cot^(2)alpha+cot^(2)beta-sqrt(2)cot alphacot beta) |
| Answer» | |
| 38896. |
Take X and Y input waveforms. Sketch the output (Z) waveform abtained from AND gate as per the following conditions: |
Answer» SOLUTION :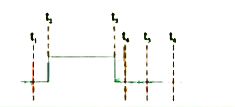
|
|
| 38897. |
Explain cleaning action of detergent ? |
| Answer» Solution :Any liquid of low surface TENSION can EASILY spread out as athin film because it.s surface energy is low. Low VALUE of surface tension also helps the liquid to penetrate narrow spaces or pores. When detergent is added to water, it.s surface tension is LOWERED. This explains the improvement in the cleaning property of the detergent solutions, compared to water. | |
| 38898. |
Determine the potential difference phi_(A)-phi_(B) between points A and B of the circuit |
| Answer» Solution :`varphi_(A)-varphi_(B)=E(C_(2)C_(3)-C_(1)C_(4))/((C_(1)+C_(2))(C_(3)+C_(4))),"when "C_(1)//C_(2)=C_(3)/C_(4)`` | |
| 38899. |
The angle of incidence at which reflected light is totally polarized for reflection from air to glass (refractive index n), |
|
Answer» `SIN^(-1)(MU)` |
|
| 38900. |
A mass of 1 kg is suspended from a spring and has a time period T on the surface of earth. The period at the centre of earth is : |
|
Answer» zero `:.` T will REMAIN same. Thus correct choice is (b). |
|



