Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3901. |
A galvanometer has coil of resistance 50Omega and shows full deflection at 100muA. The resistance to be added for the galvanometer to work as an ammeter of range 10mA is nearly |
|
Answer» `0.5Omega` in SERIES |
|
| 3902. |
Two bodies 1 and 2 of moment of inertia I_1 and I_2 have the same kinetic energy of rotation. Their angular momentum L_1 and L_2 will be in the ratio of |
|
Answer» `I_1/I_2` |
|
| 3903. |
Figure shos the characteristic curve of a junction diode. Determie the d.c. and a.c. resistance of the diode, when it operates at 0.3V. |
|
Answer» |
|
| 3904. |
The near point of a person is 50 cm and the far point is 1.5m. The spectacles required for reading purpose and for seeing distant objects are respectively. |
|
Answer» `+2D,-(2/3)D` |
|
| 3905. |
The following table has 3 columns and 4 rows. Based on table, there are three questions. Each question has four options (A), (B), (C ), and (D). Only one of these four options is correct. Pick the correct combination |
|
Answer» <P>(III) (i) (R ) |
|
| 3906. |
The following table has 3 columns and 4 rows. Based on table, there are three questions. Each question has four options (A), (B), (C ), and (D). Only one of these four options is correct. Pick the correct combination |
|
Answer» (II) (III) (Q) |
|
| 3907. |
One metallic ring of radius 1 m has a conducting rod connected between centre and rim of wheel. It rotates in a plane perpendicular to uniform magnetic field 2 T with frequency 100"rev"/s. Find emf induced across the rod. |
|
Answer» |
|
| 3908. |
Velocity of light in glass is 2 x 10^(8)m/s. From that'glass.a corivexo -convex lens is prepared, whose radius of curvatures are 15 cm and 45 cm respectively. A parallel beam-of light is incident on the lens. The beam will converge at a distance of |
|
Answer» 15 cm |
|
| 3909. |
The following table has 3 columns and 4 rows. Based on table, there are three questions. Each question has four options (A), (B), (C ), and (D). Only one of these four options is correct. Pick the correct combination |
|
Answer» (II) (i) (Q) |
|
| 3910. |
A hunter aims his gun and fires a bullet directly at a monkey on a tree. At the instant the bullet leaves the barrel of the gun, the monkey drops. Will the bullet hit the monkey ? |
|
Answer» Solution :Horizontal distance TRAVELLED `OB =x=ucos THETA t` or `t=x/(u cos theta)` For motion of BULLET from O to B, the vertical height `AB=u sin thetat -1/2 "gt"^(2)` `=u sin theta (x/(u cos theta)) -1/2"gt"^(2) =x tan theta -("gt"^(2))/2`…….(i) Also from figure MB `=x tan theta` Now, the height through which monkey falls y=MA =MB -AB `=x tan theta -(x tan theta -("gt"^(2))/2) =1/2 "gt"^(2)` 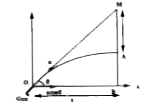 Thus, in time t the bullet passes through A a vertical distance `1/2"gt"^(2)` below M. The vertical distance through which the monkeyfall in time t. `s=1/2"gt"^(2)` Thus, the bullet and the monkey will always reach at POINT A at the same time. |
|
| 3911. |
Three equal resistors connected in series across a source of e.m.f. together dissipate 10 W power. Find the power dissipated if the same resistors are connected in parallel. |
|
Answer» Solution :`P_1 = 10 W` In series COMBINATION , total resistance = 3R Power = `P_1 = (V^2)/(3R)`  In paralle combination , total resistance = R/3 `R_2 =(V^2)/(R//3)` `IMPLIES (P_1)/(P_2) =(R//3)/(3R) implies (10)/(P_2) =(R//3)/(3R)` `(10)/(P_2) =(R)/(3xx3R) =1/9 impliesP_2 `= 90 WATTS |
|
| 3912. |
Discuss different modes of vibrations in an air column of a pipe open at both the ends. State the cause of end correction. Find the end correction for the pipe open at both the ends in fundamental mode. What should be tension applied to a wire of length 1m and maas 10 g, if it has to vibrate with fundamental frequency of 50 Hz? |
|
Answer» SOLUTION :Modes of vibration of air COLUMN in a pipe open at both ends : An open ARGAN pipe is a cylindricla tube containing an air column open at both ends. A vibrating tuning fork is held horizontally near end of the pipe. Sound waves are sent by source (vibrating tuning fork) near one end. Refer to HSC paper, July 2018, Answer 4(i). Cause of End correction : End correction arises because air particles in the plane of the open end of tube, are not free to move in all directions. Hence, reflection takes place at the plane, at small distance outside the tube. End correction for the pipe open at both ends : `v=2n_(1)L_(1)=2n_(2)L_(2)` `n_(1)L_(1)=n_(2)L_(2)` `n_(1)(l_(1)+2e)=n_(2)(l_(2)+2e)` `E=(n_(1)l_(1)-n_(2)l_(2))/(2(n_(2)-n_(1)))` or `=((n_(2)l_(2)-n_(1)l_(1)))/(2(n_(1)-n_(2)))` Numerical : We have, `l=1m,M=10g=10xx10^(-3)kg,n=50Hz` LINEAR density of wire (m) `=(M)/(l)=(10xx10^(-3))/(1)` `=10xx10^(-3)kgm^(-1)`. `impliesn=(1)/(2)lsqrt((T)/(m))` `implies50=(1)/(2)xx1xxsqrt((T)/(10xx10^(-3)))` `implies(100)^(2)=(T)/(10xx10^(-3))` `impliesT=100N`. `:.` Tension to be applied to the wire is 100 N. |
|
| 3913. |
Which is a suitable method to decrease friction |
| Answer» Answer :D | |
| 3914. |
A transistor is connected in common emitter configuration . The collector emitter voltage is 8 V and a load resistance of 800 Omega is connected in the collector circuit . The voltage drop across the load resistance is 0.5 V . If the current gain be 0.96 , the base current is : |
|
Answer» `5 MUA` `=26muA` |
|
| 3915. |
Calculate the longest wavelengths belonging to Lyman and Balmer series. Which of these wavelengths will lie in the visible region ? |
|
Answer» Solution :From Rydberg.s FORMULA , we have `1/lambda_(if)=R[1/n_f^2-1/n_i^2]` For longest wavelength in Lyman series, `n_i`=2 and `n_f` =1 `therefore 1/lambda_21=R[1/1^2-1/2^2]=3/4R` `RARR lambda_21=4/(3R)=4/(3xx1.1xx10^7)` `=1.21xx10^7` m =121 nm For longest wavelength in Balmer series, `n_i`=3 and `n_f`=2 `therefore 1/lambda_32=R[1/2^2-1/3^2]=(5R)/36` `rArr lambda_32=36/(5R)=36/(5xx1.1xx10^7)=6545xx10^(-10)` m =654.5 nm Between the TWO wavelengths , only 655 nm lies in the visible REGION. |
|
| 3916. |
A cube of side 20 cm is kept in a region as shown in the figure. An electric field vecE exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m. Find the (i) electric field vecE, and (ii) total electric flux through the cube. |
|
Answer» Solution :(i) Here potential `V=10x+5` `therefore ` ELECTRIC field `VECE= -(dV)/(dr)= -(delV)/(DEL x) hati-(delV)/(del y) hatj-(delV)/(del z)hatk=-10hatiVm^(-1)` (II) As `vecE` is directed along x-axis and is constant at all points, so we shall have flux associated with two opposite faces of cube in y-z plane. HOWEVER, flux with each of the two faces is equal but at one face it is outgoing and at the other it is incoming one. Hence, net flux `phi_(B)=0`. |
|
| 3917. |
If thermal radiation passes through free space then the temperature of the free space |
|
Answer» INCREASES DUE to collision |
|
| 3918. |
The emission of electrons from photosensitive material in an image convertor tube can be ascribed to the |
|
Answer» Photo-electric EFFECT |
|
| 3919. |
Refractive index of prism is sqrt2. One of surface of the prism is polished. If incidence angle is ......, then the ray will be reflected back. (Refraction angle is 30^@) |
|
Answer» `0^@`  Using Snell.s LAW at Q,n`=(sini)/(sinr)` `thereforesini=nsinr` `=sqrt2xxsin 30^@` `=sqrt2xx1/2=(1)/(sqrt2)` `thereforei=45^@` |
|
| 3920. |
Does the wave function y=A_(0) cos^(-2)(2pi f_(0)t(2pi x)/(lambda_(0))) represent a wve ?if yes. Then determine it's amplitude, frequency and wave-length . |
| Answer» SOLUTION :The given function can be reduced to `y=(A_(0))/(2)[1+cos{2(2pi f_(0)t-(2PIX)/(lambda_(0)))}]` The amplitude, frequency and wavelength of the wave are `(A_(0))/(2).2F(0) and (lambda_(0))/(2)`RESPECTIVELY. | |
| 3921. |
The focal lentht of a concave mirror is |
|
Answer» MAXIMUM for RED colour |
|
| 3922. |
A pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of sigma C//m^2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle beta with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)] |
|
Answer» (b). `T=2pisqrt((L)/(sqrt(g^(2)+((qE)/(m))^(2)-2g(qE)/(m)cosbeta)))` |
|
| 3923. |
A point charge of 2.0muC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface? |
| Answer» Solution :`(2.0 xx 10^(-6))/(epsi_(0)) =(2.0 xx 10^(-6))/(8.85 xx 10^(-12)) =2.26 xx 10^(5) Nm^(2) C^(-1)` | |
| 3924. |
A point charge of 5xx10^(-6)C experience a force of 2xx10^(-3) N when kept in a uniform electric field of intensity E. find E. |
|
Answer» Solution :We know that `VECF=qvecE` Where `vecF` is FORCE in NEWTON & `VECE` is strength of electric field. `rArr|vecE|=(|vecF|)/(q)=(2xx10^(-3))/(5xx10^(-6))N//C` `400N//C` |
|
| 3925. |
A parallel plate capacitorhas capacitance 1 mu F. Detereminethe displcementcurrentin thecapacitorif rateof change of voltagebetweenof 1Aflowsthroughit? |
| Answer» SOLUTION :`5 MU A ` | |
| 3926. |
A monochromatic light of wavelenght of 500nmstrikes a grating and produces foruth order bright line at an angle 30^(@). Find the number of slits per centimeter. |
|
Answer» SOLUTION :`lambda = 500 nm = 500 XX 10^(-9) m,m = 4 , theta = 30^(@)` , number of lines per CM = ? Equation for diffraction maximum in grating is, `sin theta = N m lambda` Rewriting, `N = (sin theta)/(m lambda)` Substituting, `N=(0.5)/(4xx500xx10^(-9))=(1)/(2xx4xx500xx10^(-9))=2.5xx10^(5)` lines per meter number of lines per centimeter = `2.5 xx 10^(5) xx 10^(-2)` = 2500 lines per centimetre |
|
| 3927. |
Briefly explain the two ways by which radio waves are propagated in atmosphere. |
|
Answer» Solution :Following are two WAYS for propagation of radio waves. `(a)` Ground waves ( or surface waves ) The radio waves which are travelling directly from transmitting antenna to receiving antenna following the surface of earth are called ground waves. These waves bend round the corner of the earth because the surface of earth has CURVATURE hence, the signal is absorbed by the earth and its intensity FALLS with distance and cannot travel to large distance. They have frequency upto `1500kHz` ( or wavelength above `200m`). This region is called medium wave BAND( MW band ). Sky waves. The radio waves which travel from transmitting station to receiving station by reflection from ionosphere are called sky waves. Since the DENSITY of atmosphere decreases as we go above the surface of earth so the reflection of sky wave is due to total internal reflection of the waves. These waves have frequencies more than `1500kHz` ( or wavelength less than `200m`). This region is called short wave band (SW band). |
|
| 3928. |
A charged particle is released from rest in a region of steady uniform electric and magnetic field which are parallel to each other. The particle will move in a |
| Answer» Answer :A | |
| 3929. |
A hunter aims his gun and fire a bullet directly towards a monkey sitting at a distance tree. At the intant the bullet leaves the barrel, the monkey drops, will the bullet hit the monkey ? |
| Answer» SOLUTION :Yes, BECOME the VERTICAL paths TRAVERSED by builet and monkey are same `(y=1/2g t^2)` | |
| 3930. |
What are the maximum and minimum values of power factor ? When does it occur ? |
| Answer» Solution :MAXIMUM value is 1- It happens when the circuit IA purely resistive (at resonance ). Minimum value is zero -It occurs in a purely INDUCTIVE or CAPACITIVE circuit. | |
| 3931. |
Angular momentum of a wheel changes from 2L to 5L in 3 seconds.The magnitude of torque acting on it is |
|
Answer» `L/5` |
|
| 3932. |
Two identical helium filled ballons A and B fastended to a weight of 5 gram by threads float in equilibrium as shown in fig. Calculate the charge on each ballon, assuming that theycarry equal charges. |
|
Answer» `AB = 0.6m`, C is centre of AB. `:. AC = BC = 0.3m`. `OC = sqrt(OA^(2) - AC^(2)) = sqrt(1^(2) - 0.3^(2)) = 0.954` 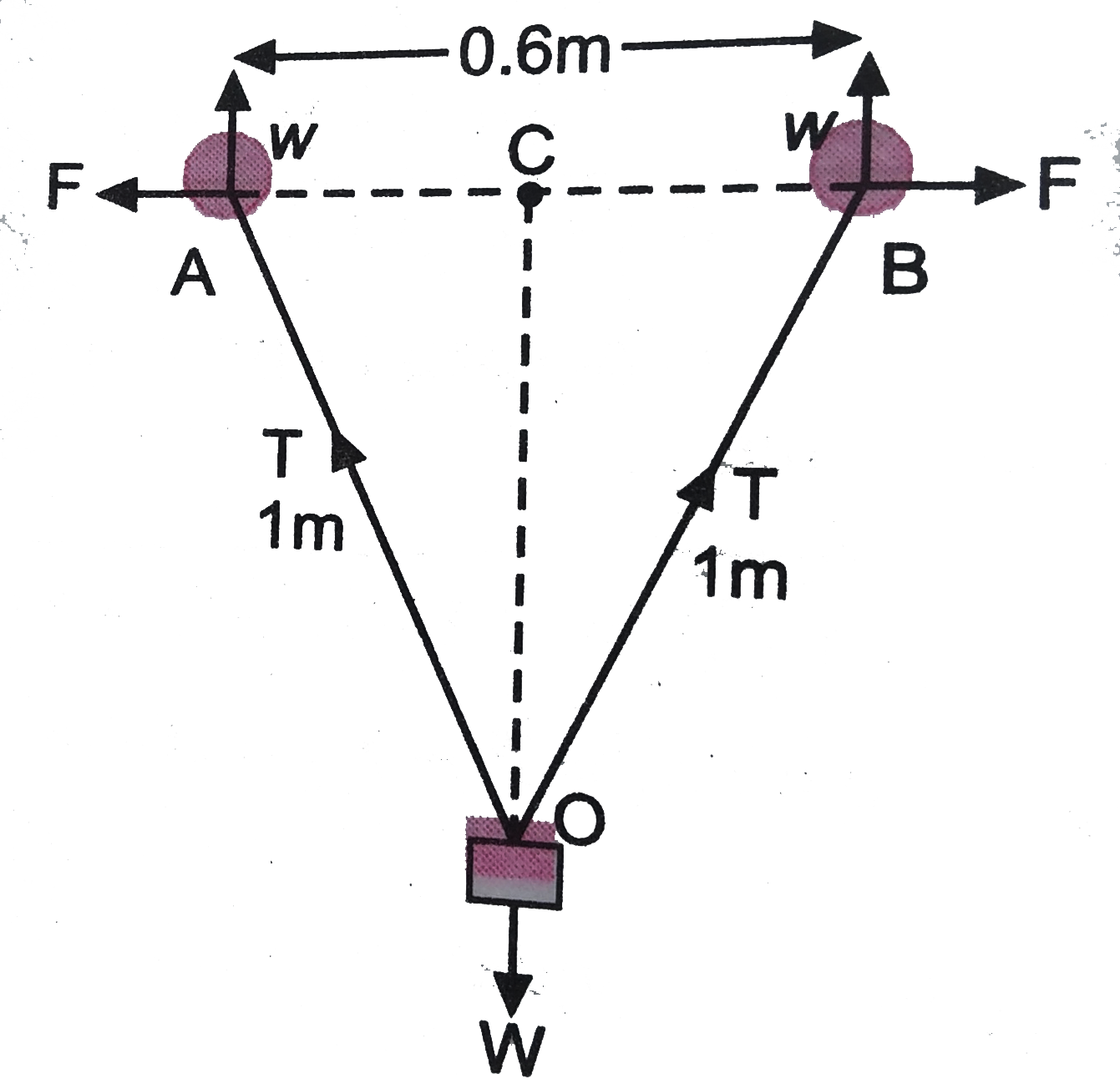 Forceof repulsionbetween flost in equilibrium, `:.` Using trianglelaw of vactors, we get `(F)/(AC) = (w)/(OC)`, where w = upthrust on each balloon. As w + w = W, `:. w = W//2` `:. F = (AC)/(OC) xx (W)/(2)` `(Q xx q)/(4pi in_(0) (AB)^(2)) = (AC)/(OC) xx (MG)/(2)` `q^(2) = 4pi in_(0) (AB)^(2) xx (AC)/(OC) xx (mg)/(2)` `= ((0.6)^(2)xx0.3xx(5xx10^(-3)xx9.8))/(9xx10^(9)xx0.954xx2)` `q^(2) = (0.36xx0.3xx49)/(9xx0.954xx2) xx 10^(-12)` `q = +- 0.56xx10^(-6)C = +-5.6xx10^(-7)C` |
|
| 3933. |
A narrow beam of natural light with wavelength lambda = 589nm falls normally on the surface of a Wollaston polarizing prism made of Iceland spar as shown in Fig. The optical axes of the two parts of the prism are mutually perpendicualr. Find the angle delta between the directions of the beams behind the prism if the angle theta is equal to 30^(@). |
|
Answer» Solution :In a uniaxial crystal, an unpolarized beam of light (or even a polarized one) splits up into `O` (for ordinary) and `E` (for extraordianary) light waves. The DIRECTION of vibration in the `O` and `E` waves are most easily spectfied in terms of the `O` and `E` PRINCIPLE planes. The principle plane of the ordianry wave is defined as the plane containing the `O` ray and the optic. Similarly the principle plane of the `E` wave is the plane contaning the `E` ray and the optic AXIS. In terms of these plane the following is true: The `O` vibrations are perpendicualr to the principle plane of the `O` ray while the `E` vibrations are in the principle plane of the `E` ray. When we apply this definition to the WOLLASTON prism we find the following: (exaggerated.) When unpolarized light enters from the left the `O` and `E` waves travel in the same direction but with different speeds. The `O` ray on the left its vibrations normal to the plane of the paper and it becomes `E` ray on crossing the diagonal boundary of the two prism similarly the `E` ray on the left becomes `O` ray on the right. In this case Snell's law is applicable only approxilately. The two rays are incident on the boundary at an angle `theta` and in the right prism the ray which we have called `O` ray on the right emerges at `sin^(-1) .(n_(e))/(n_(0))sin theta = sin^(-1) .(1.658)/(1.486) xx (1)/(2) = 33.91^(@)` where we have used `n_(e) = 1.1658, n_(0) = 1.486` and `theta = 30^(@)`. Similarly the `E` ray on the right emerges within the prism at `sin^(-1). (n_(0))/(n_(e)) sin theta = 26.62^(@)` This means that the `O` ray is incident at the bounary between the prism and air at `33.91 - 30^(@) = 3.91^(@)` and will EMERGE into with a deviation of `sin^(-1). n_(0)sin 3.91^(@)` `= sin^(-1).(1.658 sin 3.91^(@)) = 6.49^(@)` The `E` ray will emerge with an oppsite deviation of `sin^(-1). (n_(e)sin(30^(@) - 26.62^(@)))` `= sin^(-1).(1.486 sin 3.38^(@)) = 5.03^(@)` Hence `delta ~~ 6.49^(@) + 5.03^(@) = 11.52^(@)` This result is accurate to first order in `(n_(e) - n_(0))` because Snell's law holds when `n_(e) = n_(0)`. 
|
|
| 3934. |
A metallic rod of linear density is 0.25 kg m^(-1) is lylong horizontally on a smooth inclined plane which makes an angle of 45^(@) with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of strength 0.25 T is acting on it in the vertical direction. Calculates the electric current flowing in the rod to keep it stationary . |
|
Answer» Solution :The linear density of the rod I mass per UNTI length of the rod is 0.25 kg `m^(-1)` `rArr (m)/(l) = 0.25 kg m^(-1)`. Let l be the current flowing in the matallic rod. The direction of electron current is into the paper . The direction of magnetic force IB/is given by Fleming.s LEFT hand rule For equilibrum , mg sin `45^(@) - IB/ cos 45^(@)` `rArr 1 = (l)/(B) (m)/(l) G tan 45^(@) = (0.25 kg m^(-1))/(0.25 l )= 1 xx 9.8 m s^(-2)` `rArr`I = 9.8 A so, we NEED to supply current of `9 xx` A to keep the METALLIC rod stationary. 
|
|
| 3935. |
A wedge of mass m is placed on a smooth fixed horizontal surface and block of mass m is placed on smoth inclined surface of wedfe as shown. The system is then released from rest. (g is acceleration due to gravity) Select correct option(s) |
|
Answer» Shortest time in which the PERSON could swim from ONE BANK to the other (in running water) will be `12` min `:.` The compounds of accelertion of block along  and normal to incline are Hence vertical compount of acceleration of block is `a_(y) = asin^(2)theta + gsintheta costheta = (2g)/(3)` |
|
| 3936. |
The nature of the wavefront originating from a point source is: |
|
Answer» Plane |
|
| 3937. |
Define Power in AC circuits ? Derive an relation between true power & virtual power? |
|
Answer» Solution :i. Power of a circuit is defined as the rate of consumption of electric energy in thate circuit. It is GIVEN by the PRODUCT of the voltage and current. In an vary continuously with time. ii. The alternating voltage and alternating current in the series RLC circuit at an instant are given by `v=V_(m)sinomegat" and "i=I_(m)sin(omegat+phi)` iii. where `phi` is the phase angle between v and i. The instantaneous power is then WRITTEN as `P=v_(i)` `=V_(m)I_(m)sinomegat[sinomegatcosphi-cosomegatsinphi)` `p=V_(m)I_(m)[cosphisin^(2)omegat-sinomegatsinphi]` iv. Here the average of `sinomegat" over a cycle is "(1)/(2)` and that of `sinomegatcosomegat` is zero. Substituting these values, we obtain average power over a cycle. `P_(av)=V_(m)I_(m)cosphixx(1)/(2)` `=(V_(m)I_(m))/(sqrt(2)sqrt(2))cosphi` `P_(av)=V_(RMS)I_(RMS)cosphi` v. where `V_(RMS)I_(RMS)` is called apparent power and `cosphi` is power FACTOR. The average power of an AC circuit is also KNOWN as the true power of the circuit. |
|
| 3938. |
One can not see through fog, because |
|
Answer» fog absorbs the light |
|
| 3939. |
In a critical chain reaction |
|
Answer» ENERGY is released at increasing RATE |
|
| 3940. |
Some of the electric field lines of an electric dipole are given in figure. Select the correct statement from the following. |
|
Answer» (A) They are TWO CLOSED loops. |
|
| 3941. |
What is the angle between axis of rotation and magnetic axis of earth ? |
| Answer» SOLUTION :`11.3^@`. | |
| 3942. |
Using Planck's formula, find the power radiated by a unit area of a black body within a narrow wavelength interval Delta lambda = 1.0 nm close to the maximum of spectral radiation density at a temperature T = 3000K of the body. |
|
Answer» Solution :We write the required power in terms of the raadiosity by considering `DEL`only the enegry radiated in the given range. Then form the pervious problem `DELTAP = (c )/(4)overset~~(u)(lambda_(m),T)Delta lambda` `= (4pi^(2)c^(2)cancelh)/(lambda_(m)^(5)) (Delta lambda)/(e^(2ch//klambda_(m)T)-1)` But `lambda_(m)T = b` so `DeltaP = (4pi^(2)c^(2)cancelh)/(lambda_(m)^(5))(Delta lambda)/(e^(2ch//kb)-1)Delta lambda` Using the DATA `(2pic cancelh)/(kb) = (2pixx3xx10^(8)xx1.05xx0^(-34))/(1.38xx10^(-23)xx2.9xx10^(-3)) = 4.9643` `(1)/(e^(2pich//kb)-1) = 7.03xx10^(-3)` and `DeltaP = 0.312W//cm^(2)` |
|
| 3943. |
(A) : A current carrying circular loop, free to turn, when placed in an external magnetic field, orients its plane normal to field. (R) : The potential energy of the system is minimum at stable equilibrium position. |
|
Answer» Both 'A' and 'R' are true and 'R' is the CORRECT EXPLANATION of 'A'. |
|
| 3944. |
What is a radial magnetic field? Why is it required in a galvanometer ? |
|
Answer» Solution :Using concave shaped pole of magnet and placing soft IRON cylinderical core, A magnetic field, having field lines along RADII is CALLED as radial magnetic field. To make Torque independent of ‘θ’ (constant) radial magnetic field is required `tau= NIAB sin theta` for radial Magnetic Field `theta = 90^@` `tau=NIAB.` (independent of `theta`) |
|
| 3945. |
Let N be the set of natural numbers and the function f:N rarr N be defined by f (n) = 2n + 3 VV nEN. Then f is- |
|
Answer» surjective |
|
| 3946. |
In a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength lambda is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirroris 2 mm from point P. If fringe width is 0.1 mm then what is the wavelength of light used ? |
|
Answer» `3.33xx10^(-7)m` |
|
| 3947. |
If a proton had a radius R and the charge was uniformly distributed, calculate using Bohr theory, the ground state energy ofa H-atom when (i)R=0.1Å, and (ii)R=10Å |
|
Answer» Solution :In ground state of hydrogen atom, `mvr_(B)=h, v=h/(mr_(B)), and (mv^(2))/(r_(B))=(-e^(2))/(4pi in_(0)r_(B)^(2))` `:. m/(r_(B))xx(h^(2))/(m^(2)r_(B)^(2))=(e^(2))/(4pi in_(0)r_(B)^(2))` `r_(B)=(4pi in_(0))/(e^(2)) (h^(2))/m=0.51Å` `PE=-(e^(2))/(4pi in_(0)) (1/r_(B))=-27.2eV`. `KE=1/2 mv^(2)=1/2m. (h^(2))/(m^(2)r_(B)^(2))=(h^(2))/(2mr_(B)^(2))=+13.6eV` for special nucleus of radius R, If `R lt r_(B)`, ground state energy remains the same as calculated above. If `R gt gtr_(B)`: the electron moves INSIDE the sphere with radius `r_(B)'` (new Bohr radius) Charge inside `e'=e((r'_(B)^(3))/(R^(3)))` form (i) `r'_(B)=(4pi in_(0))/(e'^(2)) (h^(2))/m=(4pi in_(0)h^(2)(R^(3))^(2))/(me^(2) (r'_(B)^(3))^(2))` `(r'_(B))^(7)=(h^(2))/m((4pi in_(0))/(e^(2)))R^(6)=(0.51Å)R^(6)`.....(i) `r'_(B)=(0.51Å)^(1//7)xxR^(6//7)` If `R=0.1Å`, `r'_(B)=(0.51Å)^(1//7)xx(0.1)^(6//7)=0.126ÅgtR` If `R=10Å`, `r'_(B)=(0.51Å)^(1//7)xx(10)^(6//7)=7.19Å lt R` Now, `K.E. =1/2mv^(2)=(h^(2))/(2mr'_(B)^(2))=(h^(2))/(2mr_(B)^(2))((r_(B)^(2))/(r'_(B)^(2)))=(13.6eV) ((0.51Å)^(2))/((7.19Å)^(2))=0.068eV` `P.E.=+((e^(2))/(4pi in_(0)))((r'_(B)^(2)-3R^(2))/(R^(3)))=(e^(2))/(4pi in_(0)r_(B))[(r_(B)(r'_(B)^(2)-3R^(2)))/(R^(3))]=(27.2eV)[(0.51(7.19^(2)-300))/1000]` `=3.44eV` |
|
| 3948. |
A cyclotron's oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons ? If the radius of its 'dees' is 60 cm, what is the kinetic energy (in MeV) of the proton beam produced by the accelerator. (e=1.60xx10^(-19)C,m_(p)=1.67xx10^(-27kg),1MeV=1.6xx10^(-13)J) |
|
Answer» Solution :1. Angular frequency of a charged particle in cyclotron is, `omega=(Bq)/m` `therefore2pif=(Bq)/m` `thereforeB=(2pifm)/q` `thereforeB=((2)(3.14)(10xx10^(6))(1.67xx10^(-27)))/((1.6xx10^(-19)))` `thereforeB=6.555xx10^(-1)=0.6555T` 2. Kinetic energy of proton, `K=1/2mv^(2)` `thereforeK=1/2mr^(2)omega^(2)` `thereforeK=1/2mr^(2)(4pi^(2)f^(2))" "(becauseomega=2pif)` `thereforeK=2PI^(2)mr^(2)f^(2)` `thereforeK_(max)=2pi^(2)m(r_(max))^(2)f^(2)` `thereforeK_(max)=2pi^(2)mR^(2)f^(2)` `(becauser_(max)=R="RADIUS of DEE")` `thereforeK_(max)=(2)(3.14)^(2)(1.67xx10^(-27))(0.6)^(2)(10xx10^(6))^(2)` `thereforeK_(max)=1.186xx10^(-12)J` `thereforeK_(max)=(1.86xx10^(-12))/(1.6xx10^(-19))EV=7.412xx10^(6)eV` `thereforeK_(max)=(7.412xx10^(6))/(10^(6))MeV=7.412MeV` |
|
| 3949. |
What conclusion can you draw from the following observation on a resistor made of alloy manganin? |
| Answer» Solution :Ohm.s law is VALID to a high ACCURACY, the resistivity of the alloy MANGANIN is nearly independent of TEMPERATURE. | |
| 3950. |
In a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength lambda is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirroris 2 mm from point P. If the mirror is shifted towards left then how does the fringe pattern on screen changes ? |
|
Answer» FRINGE width decreases and the region in which interference is formed shifts downwards |
|