Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4001. |
Draw the graph showing the variation of intensity of polarised light transmitted by an analyser. |
Answer» SOLUTION :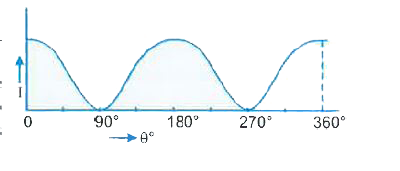
|
|
| 4002. |
एक कार विराम से गति प्रारम्भ करती है तथा उसकी चाल 10 सेकण्ड में 180 km/h तक एकसमान रूप से त्वरित होती है। कार द्वारा इस समय अन्तराल में तय की गई दूरी है |
|
Answer» 500m |
|
| 4003. |
If we consider the phasor if I in positive X-direction for an A.C. circuit which has only inductor, then the phasor of V is in ........direction . |
|
Answer» POSITIVE X |
|
| 4004. |
The displacement current was named as currentbecause |
|
Answer» it is SIMILAR to conduction curren |
|
| 4005. |
The closet distance of approach of an alpha - particle travelling with a velocity V towards a stationary nucles is .d.. For the closet distance to because d/3 towardsstationary nucleus of double the charge the velocity of projection of the alpha - particle has to be |
| Answer» Answer :B | |
| 4006. |
Show the direction of induced current in metal rings 1 and 2 lying in the sameplane where current I in the is increasing steadily. {:(1O),(to""),(2O""I):} |
Answer» SOLUTION :
|
|
| 4007. |
A plane longitudinal wave of angular frequency omega = 1000 rad/s is travelling along positive x-direction in a homogeneous gaseous medium of density d = 1 kg m^(-3).Intensity of wave is I = 10^(-10) W.m^(-2) and maximum pressure change is (DeltaP)_(m) = 2 xx 10^(-4) Nm^(-2) Assuming at x = 0, initial phase of medium particles to be zero: Amplitude of the travelling wave is |
|
Answer» `10^(-6)` m |
|
| 4008. |
The displacement X (in meters) of a body varies with time (in sec) as x=- (4)/(5)t^(2) + 16+ + 20. The velocity of body will be zero at time: |
|
Answer» 8 s Then `V=(dx)/(DT)=-(8)/(5)xxt+16` or` 0 =-(8)/(5)t +16` or `(8)/(5)t=16` or t=10 s |
|
| 4009. |
Samples of two radioactive nuclides A and B are taken. lambda_(A) and lambda_(B) are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaenously have the same decay rate at any time? |
|
Answer» Initial rate of DECAY of A is twicethe initial rate of decay of B and `lambda_(A)=lambda_(B)` |
|
| 4010. |
In Fig. 27-42, the resistances are R_1=3.00 Omega, R_2= 700 Omega. and the battery is ideal. What value of R_3 maximizes the dissipation rate in resistance 3? |
|
Answer» |
|
| 4011. |
A body is projected with a velocity 50 ms^(-1) Distance travelled in 6^(th) second is [g=10 ms^(-2)] |
|
Answer» 5 m |
|
| 4012. |
A vessel ABCD of 10 cm width has two small slits S_(1) and S_(2) sealed with identicalglass paltes ofequal thickness . The distance between the slits is 0.8 mm . POQ is the line perpendicular to the plane AB and passingthrough O , the middle point of S_(1) and S_(2) .A monochromaticlight source is kept at S , 40 cm below P and 2m from the vessel to illuminate the slits as shown in fig. The position of the cnetral bright fringe on the other wall CD w.r.t the line OQ. |
| Answer» ANSWER :D | |
| 4013. |
What mass of steam at 100^(@)C must be mixed with 250g of ice at its melting point, in a thermally insulated container, to produce liquid water at 50^(@)C ? |
|
Answer» |
|
| 4014. |
Demonstrate that in the case of a thin plate of arbitrary shape there is the following relationship 1, 2, and 3 define three mutually perpendicular axes passing through one point, with axes 1 and 2 lying in the plane of the plate. Using this relationship, find the moment of inertia of a thin uniform round disc of radius R and mass m relative to the axis coinciding with one of its diameters. |
|
Answer» Solution :(a) Let us consider a lamina of an arbitrary shape and indicate by 1,2 and 3, three axes coinciding with X, y and z-axes and the PLANE of lamina as x-y plane. Now, moment of INERTIA of a point mass about x-axis, `dI_x=dmy^2` Thus moment of inertia of the lamina about this axis, `I_x=int dmy^2` Similary, `I_y=intdmx^2` and `I_z=int dmr^2` `=intdm(x^2+y^2)` as `R=sqrt(x^2+y^2)` Thus, `I_z=I_x+I_y` or, `I_3=I_1+I_2` (b) Let us TAKE the plane of the disc as x-y plane and origin to the centre of the disc (figure). From the symmetry `I_x=I_y`. Let us consider a ring element of radius r and thickness `dr`, then the moment of inertia of the ring element about the y-axis.  `dI_x=dmr^2=(m)/(piR^2)(2pirdr)r^2` Thus the moment of inertia of the disc about z-axis `I_x=(2m)/(R^2)underset(0)overset(R)intr^3dr=(mR^2)/(2)` But we have `I_x=I_x+I_y=2I_x` Thus `I_x=I_x/2=(mR^2)/(4)` 
|
|
| 4015. |
Explain linearly polarized waves and give it definition. |
|
Answer» Solution :Consider holding a long STRING that is hel horizontally, the other end of which is to b FIXED. If we move the end of the string up and dowi in a periodic manner. A wave is generate propagating in the + x-direction as shown in figure (a).  The curves represent the displacement of a string at t = 0 and at `t=Deltat` respectively when this sinusoidal wave is propagating in the + x direction. This is shown in figure (a). In figure (b) the curve represents the time variation of the displacement at x = 0 when a sinusoidal wave is propagating in the + xdirection.  The displacement of the wave in the + xdirection OCCURS in the y-direction so its equation, `y(x,t)=asin(kx-omegat)` where a = amplitude of wave `omega=2piv` angular FREQUENCY of wave `k=(2pi)/(lamda)` wave vector and `lamda=(2pi)/(k)` WAVELENGTH According to this equation the displacement of particle of string (in y-direction) is at right angles to the direction of propagation of the wave, so it is known as a transverse wave. Here displacement is in the y-direction so it is called y-polarised wave. Since each point on the string moves on a straight line, so this wave is called a linearly polarised wave. The string always remains confined to the xyplane and therefore it is called as a plane polarised wave. If we can consider the vibration of the string in the xz-plane generating a 2-polarised wave whose displacement will be z(x,t) `=asin(kx-omegat)`. This is also the linearly polarised wave and it is transverse wave. |
|
| 4016. |
the below figure shown two closed paths wrapped around two conducting loops carrying currents i_(1)-5.0 A and i_(2) = 3.0 A . Whar is the value of the integalointvecB.dvecs for (a) path a 1and d(b) path (2) ? |
|
Answer» (B) `-1.6xx 10(-5)` T.m |
|
| 4017. |
The figure shows a network of capacitance consisting of several repetitive units shown by doted square and a capacitor capacitance C_(1) connected as end as shown in the figure. Find the value of C_(1) such that the equivalent capacitance between A and B is independent of the number of units. |
|
Answer» Solution :The equivalent CAPACITANCE between `A` and `B` will be INDEPENDENT of number of units if addition of one or more units to `C_(1)` does not change its value. The situation is shown in figure. The equivalent between `A'` and `B'` is still `C_(1)`. `(C_(1)xx2C)/(C_(1)+2C)+C=C_(1)` `RARR C_(1)=(C+-3C)/(2)` `:. C_(1)=2C`. 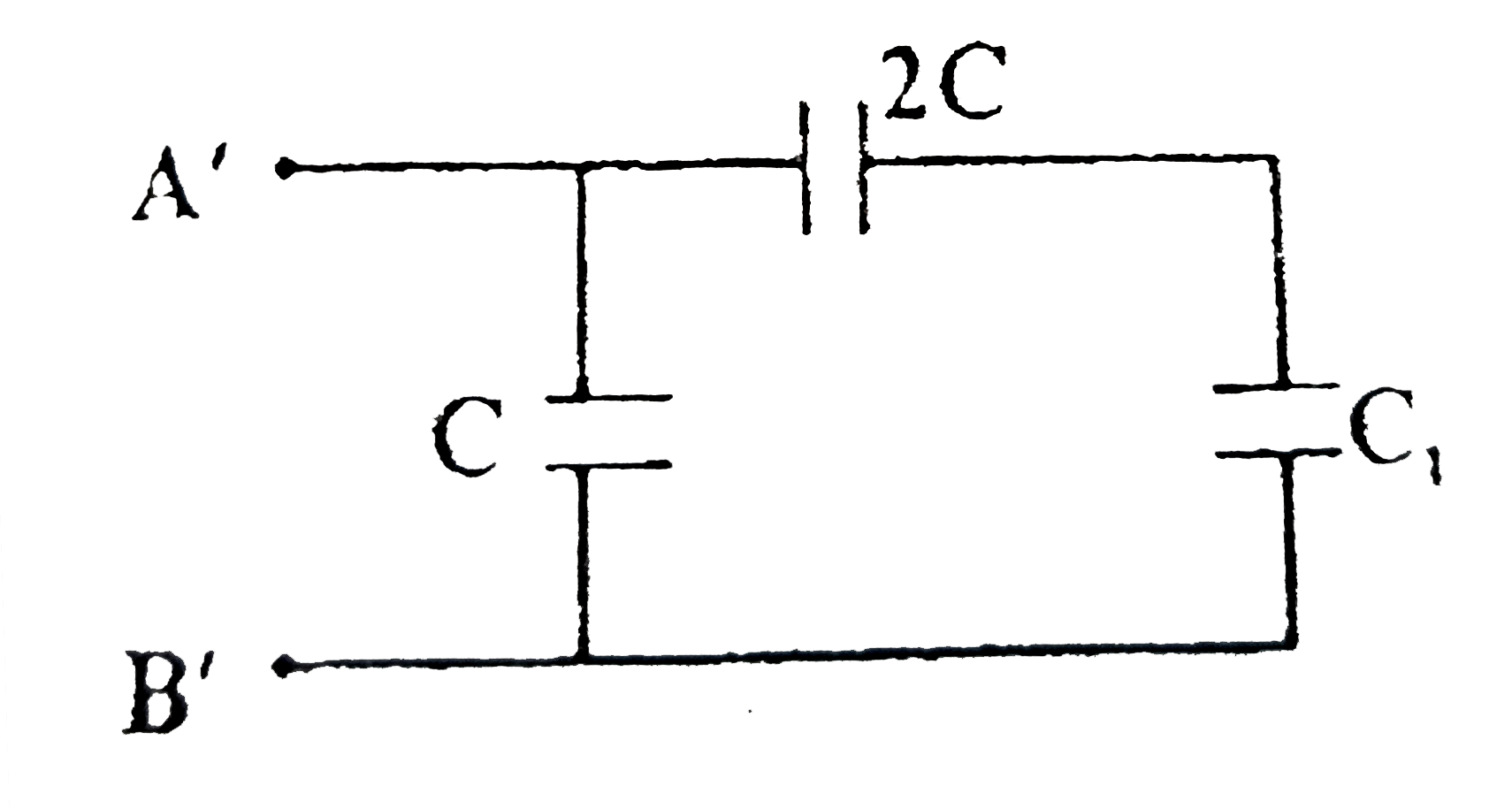
|
|
| 4018. |
The set which represents the isotope, isobar and isotone respectively is |
|
Answer» `(""_(1)H_(2), ""_(1)H^(3)),(""_(79)AY^(197),""_(80)Hg^(198)) and (""_(2)He^(3),""_(1)H^(2))` Nuclides with same mass number A but different atomic number Z are known as isobars. Nuclides with same NEUTRON number `N=(A-Z)` but different atomic number Z are known as ISOTONES. `""_(1)H^(2) and ""_(1)H^(3)` are isotopes `""_(2)He^(3) and ""_(1)H^(3)` are isobars `""_(79)Au^(197) and ""_(80)Hg^(198)` are isotones. |
|
| 4019. |
Tubes of induction starting from a charge q in a medium of dielectric constant k is , |
|
Answer» Q |
|
| 4020. |
The magnetic moment of a bar magnet of length 20cm is 3.6 xx 10^(-6)A-m^(2). The magnetic length is 90% of its geometric length. Then find the pole strength of the magnet. |
|
Answer» SOLUTION :Magnetic moment of the bar magnet ,`M=3.6 xx 10^(-6) A-m^(2)` Given that magnetic LENGTH is 90% of its geometric length . `:.` Magnet length ,`2l = (90)/(100) xx 20 =18 cm` Pole strength of the magnet `m=(M)/(2l) = (3.6 xx 10^(-6))/(18xx10^(-2)) = 2 xx 10^(-5) A-m` |
|
| 4021. |
A polaroid examines two adjacent plane polarised beams A and B whose planes of polarisation are mutually perpendicular. In the first position of the analyser, beam B shows zero intensity. From this position a rotation of 30^(@) shows that the two beams have same intensity. The ratio of intensities of the two beams I_(A)" and "I_(B) will be |
|
Answer» `1 : 3` |
|
| 4022. |
Where was the body of Bhagat Singh taken by the English forces? |
|
Answer» RIVER Ganga |
|
| 4023. |
A 50 turns circular coil has a radius of 3 cm, it is kept in a magnetic field acting normal to the area of the coil. The magnetic field B increased from 0.10 tesla to 0.35 tesla in 2 milliseconds. The average induced e.m.f in the coil is |
|
Answer» 1.77 volts |
|
| 4024. |
A meter stick is observed to be only 0.900 meters long to an inertial observer. At what speed, relative to the observer, must the meter stick be moving? |
|
Answer» `0.44xx10^(8)m//s` |
|
| 4025. |
Ferric ion forms a prussian blue coloured solution with K_(4)[Fe(CN)_(6)] due to the formation of - |
|
Answer» `K_(3)Fe(CN)_(6)` (Prussian blue) |
|
| 4026. |
A conducting sphereA of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed C is the common centre of the A and B. |
|
Answer» The FIELD is at a distance r from C, where `altrltb " ""is"(1)/(4pi epsilon_(0))(Q)/(r^(2))` |
|
| 4027. |
A concave mirror of focal length 20cm is cut into two parts from the middle and the two parts are moved perpendicularly by a distance 1cm from the previous principle axis AB. The distance between the images formed by the two parts, if the object is kept at a distance of 10cm from the pole of the original principal axis is |
|
Answer» 2cm |
|
| 4028. |
Calculate the energy released by the fission 1 g of .^235U in joule, given that the energy released per fission is 200 MeV. (Avogadro.s number =6.023xx10^23 ) |
|
Answer» Solution :The NUMBER of atoms in 1 GM of `.^235U` `="Avogadro.s number"/"Mass number"=(6.023xx10^23)/235=2.563xx10^21` Energy released per fission = 200 MEV `=200xx10^6 xx1.6xx10^(-19)=3.2xx10^(-11)` J . Energy released by 1 G of `.^235U` = Number of atoms x energy released per fission `=2.563xx10^21 xx 3.2xx10^(-11)J = 8.202xx10^10` J |
|
| 4029. |
If deflection in galvanometer in above circuit is zero then find value of R. Internal resistance of 12 V source is negligible. Will the galvanometer show some deflection if cold air is passed on10 k Omega wire wound resistor ? |
|
Answer» Solution :Here, initially when DEFLECTION in the galvanometer is zero, potential difference ACROSS R is 2V. At this time if I amount of current passes through R then, IR= 2 `rArrI = (2)/(R) ""` ....(1) Also current passing through battery is, ` I = (12)/(R + 10000 ) ""` ... (2) From equation (1) and (2), `(2)/(R) = (12)/(R + 10000) ` `therefore2 R + 20000 = 12 ` R `therefore R = 2000 OMEGA "" ` .... (3) When cold air is passed on the WIRE wound resistance, its resistance will decrease (because of decrease in temperature) which causes increase in current which then would increase potential difference across R and so some curent starts passing through galvanometer and so it will show some deflection. |
|
| 4030. |
The uncertainty in the position of a particle equal to the de-Broglie wavelength uncertainty in its momentum will be……. |
|
Answer» `(H)/(LAMBDA)` |
|
| 4031. |
Obtain the expression of electric field by a straight wire of infinite length and with linear charge density lambda. |
Answer» Solution :Consider an infinitely long thin straight wire with uniform linear charge density `lambda` 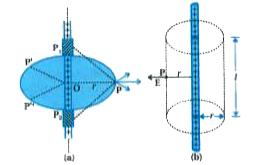 Suppose we take the radial vector from O to P and rotate it around the wire. The points P P., P" so obtained are completely equivalent with respect to the charged wire. This implies that the electric field must have the same magnitude at these points. The direction of electric field at every point must be radial (OUTWARD if `lambda gt 0`, inward `lambda lt 0` ). Since the wire is infinite, electric field does not depend on the position of P along the length of the wire. The electric field is everywhere radial in the plane cutting the wire normally and its magnitude depends only on the radial distance r. Imagine a cylindrical Gaussian surface as shown in figure. Since the field is everywhere radial, flux through the TWO ends of the cylindrical Gaussian surface is zero. At the cylindrical PART of the surface E is normal to the surface at every point and its magnitude is constant since it depends only on r. The surface area of the curved part is 2nd, where I is the length of the cylinder. Flux through the Gaussian surface, = flux through the curved cylindrical part of the surface `= E xx 2pirl` The surface includes charge equal to `lambdal`. Gauss.s law then gives, `E xx 2pirl = (lambdal)/(epsilon_(0))` `therefore E =lambda/(2pi epsilon_(0)r)` `therefore vecE = lambda/(2pi epsilon_(0)r)hatn` where `hatn`is the radial unit vector in the plane normal to the wire passing through the point. `vecE` is DIRECTED outward if `lambda`is positive and inward if `lambda` is negative. Note that it is impossible to FIND electric field at any point due to wire of infinite length, but here electric field is expressed at a point with effect of central part of wire and effect of ends is ignored. |
|
| 4032. |
A non-relativistic enters into a right-handed coordinate space with velocity 10^(4) m s^(-1) at an angle of 60^(@) with the x-axis in the xy-plane. There is a uniform magnetic field of 50 mT along the y-axis. Find the pitch of the helical trajectory. What is the axis of the helix? |
|
Answer» |
|
| 4033. |
In an organ pipe whose one end is at x = 0, the pressure is expressed byp = p_0 cos (3pi x)/(2) sin 300 omega t where xis in meter and t in sec. The organ pipe can be |
|
Answer» CLOSED at one END, open at another with length = 0.5m |
|
| 4034. |
Explain the reflection of a plane wave using Huygen's principle. |
|
Answer» Solution :Consider a PLANE wave AB incident at an angle i on a reflecting SURFACE MN. The velocity of wave in MEDIUM is v and `tau` is time to move the wavefront from POINT B to C. `:.BC=vtau`  As shown in figure plane wave AB is incident on reflective surface MN and its reflective wavefront is СE. In figure `DeltaEAC and DeltaBAC` are similar triangles, Here, `AE=BC=vtau` `angleAEC=angleABC` and AC=AC hence `angleBAC=angleECA` `:.i=r` is the law of reflection. |
|
| 4035. |
Electrical resistance of certain materials, known as superconductors , changes abruptly from a non-zero value to zero as their temperature is lowered below a critical temperature T_c (0) An interesting property of superconductors is that their critical temperature becomes smaller than T_c (0) if they are placed in a magnetic field, that is, the critical temperature T_c (B) is a function of the magnetic field strength B. The dependence of T_c(B) on magnetic field is shown in the below figure . A superconductor has T_(c)(0)=100K. When a magnetic field of 7.5T is applied, its T_(c) decreases to 75K. For this material, one can definetly say that when |
|
Answer» `B=5T, T_(C)(B)=80K` |
|
| 4036. |
A block of mass 2kg is travelling due east with velocity of 4m/s. what is the magnitude of momentum of B as seen from centre of mass frame of reference (in kg m/s). |
|
Answer» `(2G)/(5)` Momentum of B w.r.t. cm`=4[4-(13)/(5)]=(28)/(5)` |
|
| 4037. |
When filament current is increased |
|
Answer» INTENSITY of x-rays increases |
|
| 4038. |
Assertion : In interference and diffraction, light energy is redistributed. Reason : There is no gain or loss of energy, which is consistent with the principle of conservation of energy. |
|
Answer» If both assertion and REASON are TRUE and reason is the CORRECT explanation of assertion. |
|
| 4039. |
consider three charges q_(1),q_(2),q_(3)eachequal to q at the vertices of anequilateral triangleof side l what is the force on acharge Qplaced at the centroidof the triangle |
|
Answer» Solution :In thegiven EQUILATERAL triangle ABCof sides of length l if we draw a perpendicualre ADto the side BC AD=AC cos `30^(@) =SQRT(3)//2` l and the distanceAO of the CENTROID o from A is `(2/3)` AD=`(1/sqrt(3))` l by symmatry AO=BO=CO force `F_(1)` and Q due to chargeq at A=`(3)/(4piepsilon_(0))(Qq)/(l^(2))` along AO force `F_(2)` and Q due to chargeq at B=`(3)/(4piepsilon_(0))(Qq)/(l^(2))` along AO force `F_(3)` and Q due to chargeq at C=`(3)/(4piepsilon_(0))(Qq)/(l^(2))` along AO parallelogram LAW thereforethe toal force on Q =`(3)/(4piepsilon_(0))(Qq)/(4piepsilon_(0))(Qq)/(l^(2))(vecr-vecr)` =0 where `vecr` isthe unit vectoralong OA it is clear alos by symmetry that the three forces will SUM to zero considerwhat wouldhappen if the system was rotated through `60^(@)`about O |
|
| 4040. |
At a beach the light is generally partially polarized due to reflections off sand and water. At a particular beach on a particular day nearsundown the horizontal component of the electric field vector is 2.3 times the vertical component . A standing sunbather puts on polarizing sunglasses , the glasses eliminate the horizontal field component . (a) What fraction of the light intensity received before the glasses were put on now reaches the sunbather 's eyes ?(b) The sunbather still wearing the glasses lies on his side . What fraction of the light intensity received before the glasses were put on now reaches his eyes ? |
| Answer» SOLUTION :`(a) 0.16, (B) 0.84` | |
| 4041. |
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table ? Refractive index of glass = 1.5. Does the answer depend on the location of the slab ? |
|
Answer» Solution :Here real thickness of glass slab h = 15 cm, refractive index of glass n = 1.5. If the pin APPEARS to be RAISED by X cm, then apparent thickness h. = (15 - x) cm `therefore 1.5 = h/(h^(.)) = 15/(15-x) rArr x= 5 cm` The answer does not DEPEND on the location of the glass slab. |
|
| 4042. |
A body falls for 5 s from rest.If the acceleration due to gravity of earth ceases to act,the distance it travels in the next 3 s is |
|
Answer» 73.5 m |
|
| 4044. |
A single slit of width b is illuminated by a coherent monochromatic light of wavelength lambda. If the second and fourth minima in the diffraction pattern at a distance 1 m from the slit are at 3 cm and 6 cm respectively from the central maximum, what is the width of the central maximum? (i.e., distancebetween first minimum on either side of the central maximum) |
|
Answer» `1.5 cm` Wavelength of the light = `lambda` The condition for secondary minima = `b sin theta_n ~~ b theta_n = n theta` `theta_n = (n lambda)/b` For angular position of the second minima, n = 2 `theta_2 = (2 lambda)/b` For angular position of the fourth minima , n = 4 `theta_2 = (4lambda)/b` Distance of the screen from the slit, D = 1m Distance of the `n^(th)` secondary minima from the central maxima is GIVEN by `x_n = D theta_n` THUS, distance of `2^(nd)` secondary minima form the central maxima is given by : `x_2 = (2 lambda)/b xx D = (2 lambda)/b "" [ :. D = 1m]` Similarly, distance of `4^(th)` secondary minima from the central maxima is given by: `x_4 = (4 lambda)/b` Thus, the distance between fourth and second secondary minima is given by: `x_4 - x_2 = (4 lambda)/b - (2 lambda)/b = (2 lambda)/b` Given that, `x_4 - x_2= 3 cm` Thus, `(2 lambda)/b = 3 cm " or " b = (2 lambda)/((3 cm))` Width of central maxima is given by: `beta = (2 D lambda)/b = (2 lambda)/(2 lambda//(3cm)) = 3cm`. |
|
| 4045. |
What are the uses of studying hysteresis curve of substance ? |
|
Answer» Solution :Uses of hysteresis curve. The given figure shows two hysteresis CURVES, one for steel and other for iron. We find that retentivity of soft iron is higher than steel and coercivity of steel is higher than soft iron. These properties are used for making permanent magnets, core of transformers and electromagnets etc. (i) For permanent magnets. Permanent magnet should have high value of retentivity (to have large force of attraction for magnetic MATERIALS) and coercivity (to remain magnetic for long time). But coercivity is more important than the retentivity. Hence steel is preferred than iron. Now some alloys like alnico, cobalt, steel are developed which have high value of retentivity and coercivity for making permanent magnets. (ii) For electromagnets. Electromagnets are used for LIFTING heavy iron materials and are continuously subjected to cyclic changes. So the materials used for electromangets must have high value of retentivity and small hystereis loss. Hence soft iron is preferred than steel. (iii) Core of transformer. The core of transformer (TELEPHONE diaphragms and CHOKES etc.) continuously undergo many cycles of magnetisation in one second. So we use the material which has less hysteresis loss. So soft iron is used for cores of transformers, chokes etc. 
|
|
| 4046. |
A rectangular coil of 300 turns has an area of 25 cm x 10 cm. The coil rotates with a speed of 50 cps in a uniform magnetic field of strength 4 xx 10^(-2)Tabout an axis perpendicular to the field. The peak value of the induced e.m.f is (in volt) |
| Answer» ANSWER :C | |
| 4047. |
A photon with energy h omega = 1.00 MeV is scattered by a stationary free electron. Find the kinetic enegry of a compton electron if the photon's wavelength changed by eta = 25% due to scattering. |
|
Answer» Solution :The wave LENGTHS of the PHOTON has INCREASED by a fraction `eta` so its final wavelength is `lambda_(F) = (2+eta) lambda_(i)` and its enegry is `(cancelh omega)/(1+eta)` The `K.E.` of the compton ELECTRON is the enrgy lost by the photon and is `T = cancelh omega (1-(1)/(1+eta)) = cancelh omega (eta)/(1+eta)` |
|
| 4048. |
Explain how the cells are grouped in series, Obtain the condition for maximum current through an external resistor. |
Answer» Solution :Cells in series. The cell are SAID to be connected in series, if we can proceed from one point to ANOTHER through one path. Fig. shows the series combination of n cells. Here n cells, each of e.m.f. E and INTERNAL resistance r are connected to an external resistance R. 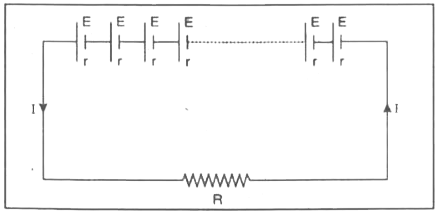 In series combination, the total e.m.f. of the cells is equal to the sum of the e.m.f.s of the individual cells. `THEREFORE` Total e.m.f. of the cells=nE Since internal resistance of all the cells are also connected in series. `therefore` Total internal resistance of the cell=nr So current flowing through the circuit, `I=(nE)/(R+nr)` CASE 1. if `R lt lt nr`, so `R=nrcongnr` `thereforeI=(nE)/(nr)=(E)/(r)` Case 2. if `R gt gt nr,` so `R+nrcongR` `therefore I=(nE)/(R)=nxx`current due to single cell. Thus in series combination of cells, to have maximum current, the total internal resistance of the cells should be negligible as compared to the external resistance of the circuit. |
|
| 4049. |
A ruby laser produces radiations of wavelenght 662.6 nm in pulses whose duration are 10^(-9)s .if the laser produce 0.39 J of energy per pulse, how many photons are produced in each pulse ? |
|
Answer» `1.3 XX 10^9` |
|
| 4050. |
If the horizontal velocity given to the satellite is lies between critical velocity and escape velocity, then the satellite performs |
|
Answer» CIRCULAR path |
|