Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1251. |
Lifting a small stone to a certain height and then dropping it downwards. What do you observe? |
|
Answer» |
|
| 1252. |
The weight of the body immersed in a liquid appears to be .............. than its actual weight. |
|
Answer» |
|
| 1253. |
A sonar deivce attached to a ship sends. Ultrasomic waves in the sea. These waves are reflected from the bottom of the sea. If the ultrasonic waves take 4 seconds to travel from the ship to the bottom of the sea and back to the ship (in the form of an echol), what is the depth of the sea? (Speed of sound in water = 1500 m//s). |
|
Answer» In a HYPOTHETICAL system , a partical of mass `m` and charge `-3 q` is moving around a very heavy partical chaRGE `q`. Assume that Bohr's model is applicable to this system , then velocuity of mass `m` in the first orbit is `(3 q^(2))/(2 epsilon_(0) h)` `(3 q^(2))/(4 epsilon_(0) h)` `(3 q)/(2 pi epsilon_(0) h)` `(3 q^(2))/(4 pi epsilon_(0) h)` A `(mv^(2))/( r) = (3 q^(3))/(4 pi epsilon_(0) r^(2)) implies m v r = (3 q^(2))/(4 pi epsilon_(0) v)` (i) Now, Speed `= ("Distance")/("Time")` So, `1500 = ("Distance")/(2)` And, Distance `= 1500 xx 2m = 3000m` Thus, the depth of this sea below the ship is 3000 METRES. |
|
| 1254. |
State two applications of universal law of gravitation. |
| Answer» | |
| 1255. |
What is the speed of the body moving with uniform acceleration at the midpoint of two points on a straight line, where the speeds are u and v respectively? |
|
Answer» Solution :LET .a. be the CONSTANT acceleration and s be the distance between the two points, From equation of motion `V^(2) - u^(2) = `2as ............ (1) Let `v_(0)` be the speed of the body at midpoint ‘M’ of the given points. Applying the same equation used above, we get `v_(0)^(2) - u^(20 = 2a (s)/(2)` From (1) , we get `v_(0)^(2) - u^(2) = (v^(2) - u^(2))/(2)` `v_(0)^(2) = (v^(2) - u^(2))/(2) + u^(2)` `v_(0)^(2) = (v^(2) - u^(2) + 2u^(2))/(2)` ` v_(0) = sqrt((v^(2) + u^(2))/(2))` 
|
|
| 1256. |
Under what condition (s) is the magnitude of average velocity of an objectis equal to its average speed ? |
| Answer» Solution :If an OBJECT moves in a straight LINE in the same DIRECTION, then the magnitude of average velocity of an object is equal to its average SPEED. | |
| 1257. |
A scooter or a motor-cycle is a compoundmachine made up of several simple machines. Study the following parts of a scooter/motor cycle and identify the simple machines involved in them. (i) Clutch levers(ii) Throttle (iii) Front brake lever(iv) Rear brake pedal (v) Stand(vi) Rear view mirror (vii) Wheels(viii) Chain drive A person weighing 50 kg, moves on a scooter of 100 kg at a speed of 36 km h^(-1) and applies brakes to stop within a distance of 10m. If the mechanicaladvantage of the brake system (comprising brake drum, lever, etc.) is 10^(3), find the force with which the person should press the foot pedal to stop the vehicle. |
|
Answer» SOLUTION :(i) Equations of motion, Newton's SECOND law of motion and principleof moments. (ii) Calculate retardation using` a = (V^(2)-u^(2))/(2S)` `(iii) Calculate the braking (retarding ) force using F = M.A., where 'm' is the combined mass of the SCOOTER and the person. (iv) Calculate effort using: effort = load/M.A. = F/M.A. (v) 1.5 N |
|
| 1258. |
Compare the time periods of two simple pendulums of length 1 m and 16 m at at place. |
|
Answer» Solution :Given:`l_1 = 1 m and l_2 = 16 m` Since `T PROP sqrtl THEREFORE (T_1)/(T_2) = sqrt((l_1)/(l_2))` `therefore (T_1)/(T_2) = sqrt(1/(16)) = 1/4 `i.e. `T_1: T_2= 1:4` |
|
| 1259. |
Find the energy in kwh consumed in 10 hours by four devices of power 500w each. |
|
Answer» Solution :ENERGY consumed by an electric DEVICE can be obtained with the help of the expression for power, P = w/t Where power rating of the device, p = 500w = 0.50 kw Time for which the device runs, T = 10h. Work done =energy consumed by the device. Therefore, energy consumed = Power `xx` Time = `0.50 xx 10 = 5kwh` Hence, the energy consumed by FOUR equal rating devices in 10h will be `4 xx 5 KWH = 20 kwh - 20 units` |
|
| 1260. |
When a stone of mass 50 kg and another of mass 5kg fall down simultaneously form the top of a fivestorey building, which one will reach the ground first? |
|
Answer» REASON: Acceleration due to gravity does not depend on the mass of the body. It will be the same for allGMbodies falling to the earth. `g=GM/R^2` |
|
| 1261. |
Which of the following has more inertia: |
|
Answer» RUBBER BAIL |
|
| 1262. |
A train starting from a railway station attains a velocity of 30 ms^(-1) in one minute. What is its acceleration ? |
|
Answer» SOLUTION :`a = (v-u)/(t)` Here,` u =0, v = 30 MS ^(-1) and t= 1 min = 60 sec = (30-0)/(6) = 0.5 ms ^(-2).` The acceleration PRODUCED in the train 3 is 0.5 `ms^(-2).` |
|
| 1263. |
A bus travels, a distance of 20 km from Chennai central to airport in 45 minutes. What is the average speed? |
|
Answer» Solution :Given : Distance =20 km =20,000 m Time =45 min=2700 s AVERAGE SPEED =`"Total Distance"/"Total Time Taken"` Average speed = `"20 km"/"40 min"="20,000m"/"2700 s"` `="200 m"/"27 s"=7.4 ms^(-1)` |
|
| 1264. |
An artificial satellite is moving in a circular orbit of radius 42,250 km. Calculate its speed if it takes 24 hour to revolve around the earth. |
|
Answer» Solution :Here,` r = 42,250 KM = 42250 XX 1000 m ` Time taken for one rovolution `= 24 H = 24 xx 60 xx 60 s` Speed (u) `= ("Distance")/("Time") = (2pi r )/("Time") = (2 xx (22)/(7)xx 42250 xx 1000 m )/( 24 xx 60 xx 60 s) ` `~~3073.74 ms ^(-1)` The speed of the satellite is `3073.73 ms ^(-1)` |
|
| 1265. |
A boy holds a convexlens 30 cm above the base of an empty vessel. Thereal image of thebottom of thevessel is formed20 cm abovethe lens.The boy fills aliquid in thevessel up to a depth of 25 cm and finds thatthe real image of thebottom of the vessel is now 30 cm above the lens. Find the refractive index of theliquid. |
|
Answer» Solution :(i) Let the focal length of the lens be f. ` f = (v_(1)v_(1))/(v_(1) - u_(1)) ` Determine the value of f andlet THEBOTTOM of the vessel appear to be at a DEPTH `'u_(2)'` from thelens when the beaker is filled with a liquid. ` 1/u_(2) = 1/v_(2) - 1/f` where `v_(2)` is theimage distance when thebeaker is filled with water. Now theshift of thebottom of the vessel= `u_(1) - u_(2)` The apparent depth of thewater in the container= `d - (u_(1) - u_(2))` where 'd' is thedepth of thewater in thecontainer. `:. " REFRACTIVE index " = ("Real depth")/("Apperent depth") = d/(d-(u_(1)-u_(2)))` (ii) ` mu = 1.66or 5/3` |
|
| 1266. |
Fill in the following blanks with suitable words : (a )Force acting on a units area is called …….. (b) It is the …..force which makes objects appear lighter in water (c ) A heavy ship floats in water because its ………….density is less thanthat of water . (d ) In fluids (liquids and gases ), pressure acts in .........direction ,and pressure .....as the depth increases, (e ) In order to sink in fluid ,the density of an object must be .........than the ...... of the fluid . (f ) snow shoes work by spreding out a preson's ........over a much bigger .......... |
|
Answer» |
|
| 1267. |
A car moves with constant speed of 10 m/s in a circular path of radius 10m. The mass of the car is 1000 kg. How much is the required centripetal force for the car? |
| Answer» SOLUTION :`10^(4)N` | |
| 1268. |
The distance between Ahmedabad and Vadodara is 100 km. A scooterist travels at the average speed of 50 km h^(-1). If he travels first 60 km at a uniform speed of 45 kmh^(-1), what will be his speed for the remaining distance ? |
| Answer» SOLUTION :`60 KM H ^(-1)` | |
| 1269. |
Calculate the weight of a body in the moon if it weights 150 kg in earth? |
|
Answer» |
|
| 1270. |
Which of the following can produce longitudinal waves as well as transverse waves under different conditions? |
|
Answer» water |
|
| 1271. |
Name the mirror(s) that can give (I) am erect and enlarged image, (ii) same sized, inverted image. |
| Answer» SOLUTION :CONCAVE MIRROR | |
| 1272. |
State Newton's laws of motion |
|
Answer» Solution :I law : An object remain in a stateof rest or a uniform motion in a straight line unless ACTED UPON by an external unbalanced force. II law : The rate of momentum of an object is proportional to the APPLIED unbalanced force in the direction of the force. III law : To every action , there is an equal and OPPOSITE reaction and they act on two DIFFERENT bodies. |
|
| 1273. |
Which of the following device does not work on reflections of sound waves? |
|
Answer» stethoscope |
|
| 1274. |
Draw a graphical represntation of the wave shape for (a) low pitched sound (b) a high pitched sound. |
|
Answer» 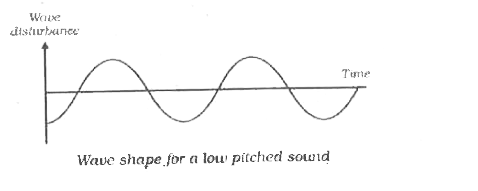 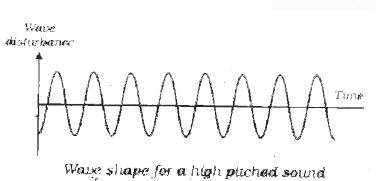
|
|
| 1275. |
How do green plants produce food? |
| Answer» Solution :The green leaves of plants USE solar ENERGY to MAKE their food through the PROCESS of photosynthesis. | |
| 1276. |
When an object is fully submerged in strong salty water, it undergoes an apparent: |
|
Answer» LOSS in mass |
|
| 1277. |
What are electric lines of force? |
| Answer» Solution :The direction of the electric FIELD is the direction OFTHE force that WOULD ACT on a small positive charge. Therefore, the lines REPRESENTING the electric field are called .electric lines of force.. | |
| 1278. |
Which characteristic of the sound helps you to identify your friend by his voice while sitting with others in a dark room ? |
| Answer» SOLUTION :QUALITY (or TIMBRE) of SOUND. | |
| 1279. |
The mass per unit volume of a substance is called density. |
|
Answer» SOLUTION :(density = mass / VOLUME) Arrangethe following in order of increasing density. Air, EXHAUST from chimney, HONEY, water, chalk, cotton and iron. Exhaust from chimney `{:("Air", "Water"),("Honey", "Chalk"),("Cotton", "Iron"):}` |
|
| 1280. |
What are the effects of electric current? |
| Answer» Solution :when current FLOWS in a circuit, it exhibits various effects. The MAIN effects are, HEATING, chemical and MAGNETIC effects. | |
| 1281. |
An object of mass 100 kg is accelerated uniformly from a velocity of 5 m s-1 to 8 m s ‘ in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object. |
| Answer» | |
| 1282. |
At what speed a person having 60 kg mass should run to acquire 750 J kinetic energy? |
|
Answer» |
|
| 1283. |
A motorcycle travelling at 20 ms^(-1) has an acceleration of 4 ms^(-2). What does it explains about the velocity of the motorcycle? |
| Answer» SOLUTION :It explains that the MOTORCYCLE TRAVELS with uniform velocity. | |
| 1284. |
In an experiment to determine the densities, four solids A,B,C and D are immersed in a liquid contained in a measuring cylinder one by one. The volume of water displaced by the solids A,B, C and D are 100 cm^(3), 100 cm^(3), 80 cm^(3) and 80 cm^(3), respectively. When weighed in air, the masses of solids A,B,C and D were found to be 80g,100g,100g and 80g, respectively. The two solids having identical densities are: |
|
Answer» A and C |
|
| 1285. |
If 15 g of a saturated solution of sodium chlroide at 20^(@)C, leaaves a solid residue of 3 g, when evaporated to dryness, calculate the solubility of NaCl at that temperature. |
|
Answer» Solution :WT. of water in solution=`15-3=13g,""So," "12g" "H_(2)O` DISSOLVES 3g of SOLID `therefore 100" g "H_(2)O" dissolves "(3)/(12)xx100g` of solid `=25g``therefore` solubility in % (w/w)=25. |
|
| 1286. |
Does sound follow the same laws of reflection as light does ? Explain. |
|
Answer» |
|
| 1287. |
In a 100 m race, the winner takes 10s to reach the finishing point. The average speed of the winner is ______ ms^(-1) |
|
Answer» 5 |
|
| 1288. |
An object travels 16 m in 4s and then another 16 m in 2 s. What is the average speed of the object? |
|
Answer» Solution :Total distance travelled by the object `= 16 m + 16 m = 32 m` Total time taken `= 4 s + 2S = 6s` Average speed `V _(av) = ("Total distance travelled")/("Total time taken") = (32m)/(6s) = 5.33 MS ^(-1)` `THEREFORE` Therefore, the average speed of the object is `5.33 ms ^(-1).` |
|
| 1289. |
Speed (s), wave length(lambda) and frequency (upsilon)of sound are related as |
|
Answer» `S= U XX UPSILON` |
|
| 1290. |
A man first swims in sea water and then in river water. (i) compare the weights of sea water and river water displaced by him. (ii) Where does he find it easier to swim and why? |
|
Answer» |
|
| 1291. |
Rubbing a comb on hair makes the comb get -0.4C. (a) Find which material has lost electron and which one gained it. (b) Find how many electrons are transferred in this process. |
|
Answer» Solution :(a) The material is COMB which GAINED electrons and the HAIR gained it. (b) Charge on 1 electron, `e= 1.6xx10^(-19)C` `q= "ne or "n=q"/"e` `n= 0.4"/"1.6xx10^(-19)=0.25xx10^(19)` `=2.5xx10^(18)`. |
|
| 1292. |
What is a positive and a negative ion? |
| Answer» Solution :If an ELECTRON is removed from the atom, it BECOMES POSITIVELY charged. Hence it is CALLED a positive ion. When an electron is added to an atom, it becomes negatively charged. Hence it is called a negative ion. | |
| 1293. |
Find out the displacement between 10 s and 20 s from the graph. |
|
Answer» |
|
| 1294. |
A hydraulic system is used to lift a 2000 kg vehicle in an auto garage. If the vehicle sits on a piston of area 0.5 m^(2) ,m, and a force is applied to a piston of area 0.03m^(2) , what is the minimum force that must be applied to lift the vehicle?Given: Area covered by the vehicle on the piston A_(1) = 0.5 m^(2) Weight of the vehicle , F_(1) = 2000 kg xx 9.8 m s^(-2) Area on which force F_(2) is aplied , A_(2) = 0.03 m^(2) |
|
Answer» Solution :`P_(1) = P_(2) , F_(1)/A_(1) = F_(2)/A_(2) " and " F_(2) = F_(1)/A_(1) A_(2) ` , ` F_(2) = (2000 XX 9.8) (0.03)/(0.5) = 1176 ` N |
|
| 1295. |
A rectangle glass wedge (prism) is immersed in water as shown in figure E-a. For what value of angle alpha, will the beam of light, which is normally incident on AB, reach AC entirely as shown in figure E-b. Take the refractive index of water as 4/3 and the refractive index of glass as 3/2. |
Answer» Solution :From the geometry of figure E-b it is CLEAR that, the angle of incidence on the side BC is EQUAL to `alpha` (dotted line is a normal drawn at the POINT of incidence). The ray should undergo total internal reflection to reach AC. For occurrence of total internal reflection, the value of `alpha` must be greater than the critical angle at interface of water and glass. 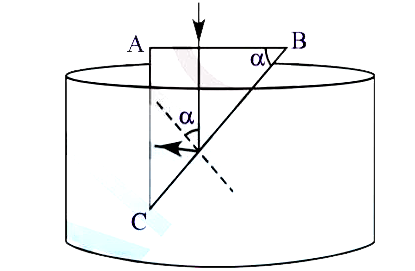 LET .C. be the critical angle of interface of glass and water. From the given condition `alpha gt C .......(1)` We know, `sin C=1/(n^(12))` ........(2) `n_(12)=3/2 / 4/3=9/8` From equation 2, we get `sin C=8/9 rArr C=62^(@)30^(1)` Hence `alpha` is greater than `C=62^(@)30^(1)` Let us see few activities of total internal reflection. |
|
| 1296. |
A motorcycle moving with a speed of 5 ms^(-1)is subjected to an acceleration of 0.2 ms^(-2) for 10 second. Calculate (a) the speed (b) the distance travelled. |
|
Answer» Solution :Here,` u = 5 ms ^(-1),a =0.2 ms ^(-2), t = 10` second `(a) v = u + at ` `= 5 ms ^(-1) + 0.2 ms ^(-2) xx 10 s ` ` = 5 ms ^(-1) + 5 ms ^(-1) = 10 ms ^(-1)` (b)` s = ut + 1/2 at ` `= 5 ms ^(-1) + 10S + 1/2 xx 0.2 ms ^(-2) xx (10 s ) ^(2)` `= 50 m + 10 m = 60 m` The speed of the MOTORCYCLE after 10 second is `10 ms ^(-1),` the distance TRAVELLED by the motorcycle is 60 m. |
|
| 1297. |
Suppose the weight of a man on the planet A is half than that on the earth. If he can jump 0.4 m high on earth's surface, then how high he can jump on the planet A? |
|
Answer» `therefore (mg_(1)h_(1))_("earth")=(mg_(2)h_(2))_("planet "A)` `therefore (mg_(1))h_(1)=((mg_(1))/(2))h_(2)` `therefore 2h_(1)=h_(2)` `=2xx0.4m` `therefore h_(2)=0.8m` |
|
| 1298. |
When the reflecting surface is curved outwards the mirror formed will be ....................... · |
|
Answer» CONCAVE mirror |
|
| 1299. |
State the units of speed |
| Answer» Solution :The SI units of SPEED is m/s `(ms^(-1)).` The unit km/H (`km h^(-1))` is also USED. | |
| 1300. |
A person walks 50 m in the north direction and from there he walks 30 m in the west direction. Now, he/she walks 50 m distance in south direction. Find the distance travelled by the person and his/her displacement. Find out the average speed and average velocity of person if he/she takes 100 s time to move from initial to final position. |
|
Answer» Solution :Total DISTANCE = 130m, displacement =0 Average SPEED `= 1.3 ms ^(-1),` Average velocity `= 0.3 ms ^(-1)` |
|
 If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i)
If `V_(2) = 2V_(1) and T_(2)=3T_(1)`, then the energy stored in the string is `1/4 P_(1)V_(1)` If `V_(2) and 2V_(1)` and `T_(2) = 3T_(1)`, then the charge in iternal energy is `3P_(1)V_(1)`. If `V_(2)=3V_(1)` and `T_(2) = 4T_(1)`, then the work done by the gas is `7/3 P_(1)V_(1)` If `V_(2) = 3V_(1)` and `T_(2) = 4T_(1)`, then the heat supplied to the gas is `17/6 P_(1)V_(1)`. B From gas equation , `(P_(1)V_(1))/(T_1) = (P_(2)V_(2))/(T_2) = nR or P_(2) = (P_(1)V_(1)T_(2))/(V_(2)T_(1)) ` ...(i) 
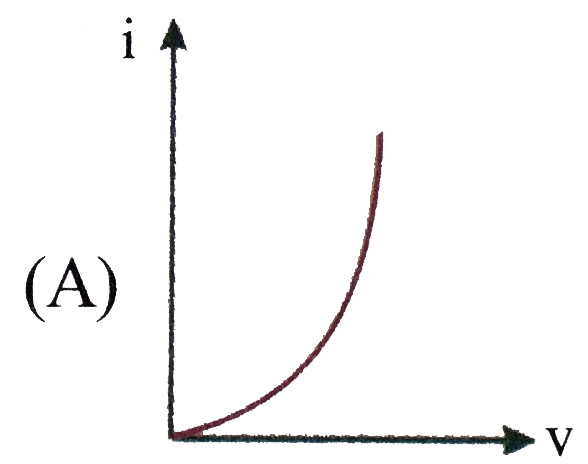

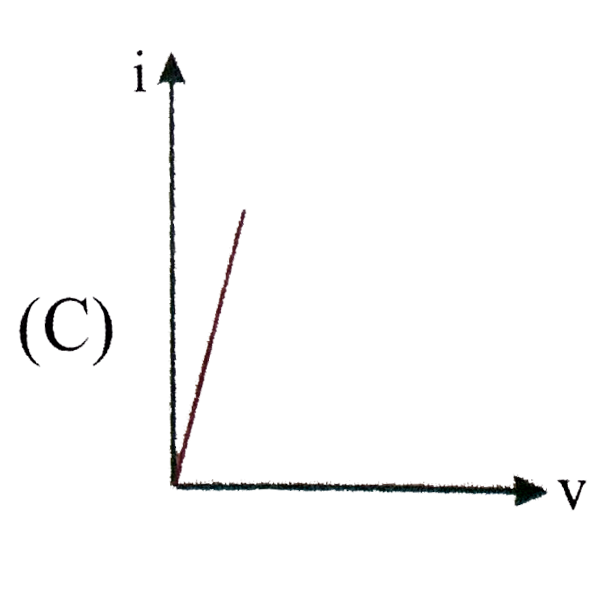
 C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of
C As ammeter has very low resistance most of current will pass through the ammeter so reading of ammeter (`i`) will be very large. Voltmeter has very high resistance so reading of voltmeter will be very low.Unit of `(CV)/(rho epsilon_(0))` are of  `P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the
`P_(2)` `P_(1)` `(P_(1)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` `(P_(2)(V_(0)/(2))^(lambda))/((V_(0)/(2)+Ax)^(lambda))` CIn the 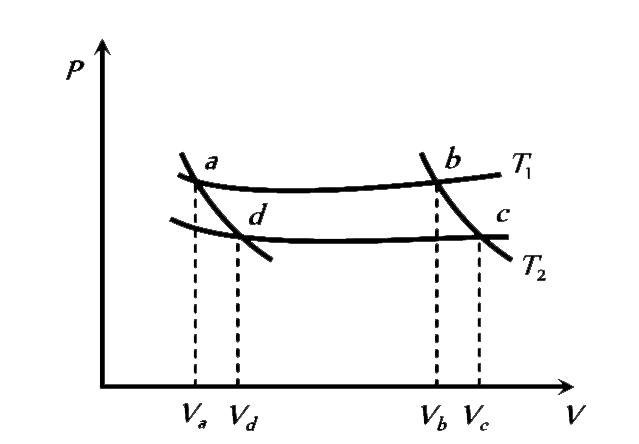 `(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it
`(V_(b))/(V_(c))` `(V_(c))/(V_(b))` `(V_(d))/(V_(a))` `V_(b)V_(e)` AA light ray from air is incident (as shown in figure) at one end of a glass fiber (refractive index `mu = 1.5`) making an incidence angle of `60^(@)` on the lateral surface, so that it undergoes a total internal reflection. How much time would it  `3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is
`3.33 mu sec` `6.67 mu sec` `5.77 mu sec` `3.85 mu sec` D N/AA combination of two thin lenses with focal lengths `f_(1)` and `f_(2)` respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm . The corresponding values of `f_(1)` and `f_(2)` are 30 cm, -60 cm 20 cm, -30 cm 15 cm, -20 cm 12 cm, -15 cm B N/AAn optical instrument uses a 25 D objective and 20 D eyepeice with a tube length of 25 cm when eye is least strained The instrument is a telescope with angular magnification 20. The instrument is a microscope with angular magnification 20. The instrument is a telescope with angular magnification 24. The instrument is a microscope with angular magnification 24. B N/AThe ratio of d-Brogile wavelength off mlecules of hydrogen and helium gas moving at arms speed in two gas jars kept sparately at temeperature `37^(@)` C and `127^(@)` C respectively is : `(2)/sqrt(3)` `sqrt(2/(3))` `sqrt(3)/(2)` `sqrt(8/(3)` DAt t=O, light of intensity `10^(12)` photons/` s-m^(2)` of energy 6eV per photon starts falling on a plate with work founction `2.5 eV` If area of the plate is `2xx10^(-4) m^(2)` and for every `10^(5)` photons one photoelectron is emitted, charge on the plate at t=25 s is `8xx10^(-15) C` `4xx10^(-14) C` `12xx10^(-10) C` `16xx10^(-12) C` ARadius of an electron moving in a circle in constant magnetic field is two times that of an `alpha` particle in the same field. Then de-Broglie wavelength of electrons is x-times of the `alpha`-particle Here x is1A telescope has an objective lens of `10cm` diameter and is situated at a distance of one kilometre from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is `5000 Ã…`, of the order of mm is :5 Resolving limit of telescope is  30 N//A
30 N//A