Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

2901.

consider the function f(X) =x+cosx -a which of the following is not true about y =f(x)?

Answer»

It is an increasing function
It is a monotonic function
It has infinite POINTS of INFLECTION s
None of these

Solution :`f(x)=x+cosx-a or f(X)=1 -SINX ge 0 FORALL x in R`
Thus f(X) is increasing in `(-oo,oo)` as for f(x) =0 x is not forming an interval also
f(X) =-cos x =0
or `x =(2n+1)(pi)/(2),nin Z`
Hence there are infinite points of inflection
Now f(x) =1-a
For positive root `1-alt0 or agt1` for negative root `1-agt 0 or a lt1`
Discussion
2902.

Find the coefficient of x^6 in (1+ x + x^2 + x^3+…….oo)(1+x^2 +x^4 + x^6 + ……oo)

Answer»


ANSWER :4
Discussion
2903.

The tangents at the points t_(1) and t_(2) on the parabola y^(2)=4ax are at right angles then:

Answer»

`t_(1)t_(2)=-2`
`t_(1)t_(2)=2`
`t_(1)t_(2)=-1`
`t_(1)t_(2)=1`

ANSWER :C
Discussion
2904.

Number of five digit integers, with sum of the digits equal to 43 are :

Answer»

5
10
15
35

Answer :C
Discussion
2905.

Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is (2R)/(sqrt(3)). Also find the maximum volume.

Answer»


ANSWER :`(4PI R^(3))/(3sqrt(3))`
Discussion
2906.

IFx^2 - 4x - 12sqrt( x^2 - 4x +19) + 51 =0thenx=

Answer»

`1 OR3 or - 5 or9`
`2 or-3or 5or 7`
`-3 or1 or-7`
none

Answer :A
Discussion
2907.

If f : R rarr Rbe the function defined by f(x) = sin (3x +2) AA x in R. Then , f is invertible.

Answer»


SOLUTION :N/A
Discussion
2908.

The radius of the circle passing throught the foci of the ellipse x^(2)/16+y^(2)/9=1 and having its center at (0,3) is

Answer»

6
4
3
2

Answer :B
Discussion
2909.

Find the unique antiderivative F(x) of f(x)=2x^2+1, whese F(o)=-2.

Answer»

Solution :`F(x)=INTF(x)DX=int(2x^2+1)dx`
=`2/3 x^3+x+C`
But F(o) =-2
`THEREFORE` -2=C
Thus `F(x) =`2/3 x^3+x-2`
Discussion
2910.

If the position vectors of three points A, B, C respectively are hati+2hatj+hatk,2hati-hatj+2hatk and hati+hatj+2hatk, then the perpendiculardistance of the point C from the line AB is

Answer»

`SQRT((3)/(11))`
`sqrt((4)/(11))`
`sqrt((6)/(11))`
`sqrt((8)/(11))`

ANSWER :C
Discussion
2911.

Let R rarr R be a continuous function define by f(x ) =(1)/(e^(x)+2e) statement 1 : f(c )=1/3 for some c in R statement 2 0 lt f(x) le (1)/(2sqrt(2))for all x in R

Answer»

statement -1 is truestatement 2 is truestatement2 is not the correct EXPLANATION for statement -1
statement-1 is truestatement -2 is FALSE
statement -1 is falsestatement 2 is true
statement -1 is true statement -2 is true statement -2 is thecorrectexplantion for statement -1

Answer :D
Discussion
2912.

int_(0)^(5)x(5-x)^(10)dx=

Answer»

`(5^(12))/(132)`
`(5^(10))/(132)`
`(1)/(132)`
`(5)/(132)`

ANSWER :A
Discussion
2913.

Line OQ is angle bisector of angle O of right angle triangle OPR, right angle at P. Point Q is such that ORQP is concyclic. If point O is orign and points P,Q,R are represented by the complexnumbers z_(3),z_(2),z_(1) respectively. If (z_(2)^(2))/(z_(1)z_(2))=3/2 then (R is circum radius of /_\OPR)

Answer»

Angles of `/_\OPR` are `(pi)/6,(pi)/3,(pi)/2`
Angles of `/_\OPR` are `(pi)/4,(pi)/4,(pi)/2`
Area of `/_\OPR` is `2sqrt(2)R^(2)`
Area of `/_\OPR` is `2R^(2)`

Solution :By Rotation theory
`(z_(2))/(z_(1))=costhetae^(itheta)`
`(z_(3))/(z_(1))=(COS2THETA)/(costheta).e^(itheta)`
So `(z_(2)^(2))/(z_(3)z_(1))=(cos^(2)theta)/(cos2theta)=3/2`
`theta=(pi)/6`
Discussion
2914.

Differentiate cos(sqrtx) w.r.t.x

Answer»

SOLUTION :`d/dx[COS(SQRTX)]=-SIN(sqrtx)d/dx(sqrtx)=-sinsqrtx1/(2sqrtx=(-sinsqrtx)/(2sqrtx)`
Discussion
2915.

Solve x^(9)-x^(5)+x^(4)-1=0

Answer»


ANSWER :`x=cos.(2kpi)/(4)+ISIN.(2kpi)/(4)` `k=0,1,2,3`
`x=cos.((2k+1)PI)/(5)+isin((2k+1)pi)/(5)` `k=0,1,2,3` and `4`
Discussion
2916.

Two cards drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black .

Answer»


ANSWER :`(25)/(102)`
Discussion
2917.

For0 lt x lt pi/2, int _(1//sqrt2) ^(1//2) cot x s (cos x )equal to

Answer»

`(SQRT3-sqrt2)/(2)`
`(sqrt2- sqrt3)/(2)`
`(1- sqrt3)/(2)`
None of these

ANSWER :B
Discussion
2918.

The points a-2b+3c, 2a+3b-4c, -7b+10 c are

Answer»

COLLINEAR
non-collinear
can't say
None of these

Solution :Let the given points be A, B and C and O be the origin.
Then, `OA=a-2b +3c`
`OB=2a+3b-4c`
and `OC=7b+10c`

Now, `AC+OC-OA`
`="("-7b+10c-(a-2b+3c)`
`=-a-5b+7c`
`AB=OB-OA`
`=(2a+3b-4c)-(a-2b+3c)`
`=a+5b-7c`
`:. AB =-AB =(-1) XX AC`=scalar `xx AC`
HENCE, the points A, B and C are collinear.
Discussion
2919.

As soon as you cross the river, you find a Kabuliwala. You ask him for help to reach Kabul as soon as possi- ble. He says that he will show you the way to Kabul if you help him with the answer of a question. First he explains you the game of CROSS- ZERO. “This game is played on a matrix of 3x3. In this game, the players try to get three circles or three crosses in a row (horizontal, vertical, or diagonal). A player always tries to win, i.e., if a player can place his own symbol (X or O) in a row that already contains two of his own symbols, he will do so. A player always tries to avoid that his opponent wins, i.e., if a player can place his own symbol (X or O) in a row that already contains two of the symbols of his opponent, he will do so.” The question he asks is that Khaled and Shahzia play a game of Cross-Zero. Khaled plays with crosses (X) and Shahzia plays with circles (O), however we don’t know who started the game. The players are intelli- gent enough and maintain the rules. After six turns into the game the matrix looks like- So who will win the game ?

Answer»

Any one can win depending on the initial move
Khaled
Shahzia
The game will RESULT in a draw.

Solution :C
It is clear that if we know who made the sixth move, we also know who can make the seventh move andwins. If Shahzia (circles) has made the sixth move, there are three possibilities for the situation after five moves: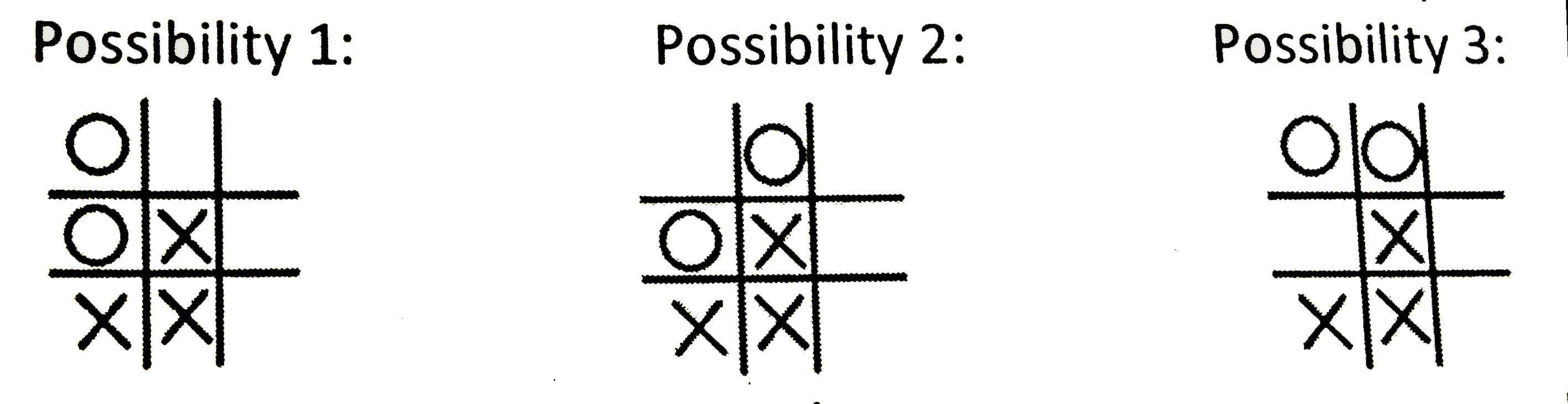

Based on the rules of the game, only possibility 1 could have resulted in the situation after six moves. Inthat case, there are three possibilities for the situation after four moves:
Based on the rules of the game, Khaled (crosses) would have made the winning move, which however did not happen. From this, we can conclude that Khaled did not make the fifth move and Shahzia did not make the sixth move. THEREFORE, Khaled must have made the sixth move and Shahzia can make the seventh, winning move! To CHECK that Khaled could indeed have made the sixth move, we look at the following three possibilities after five moves: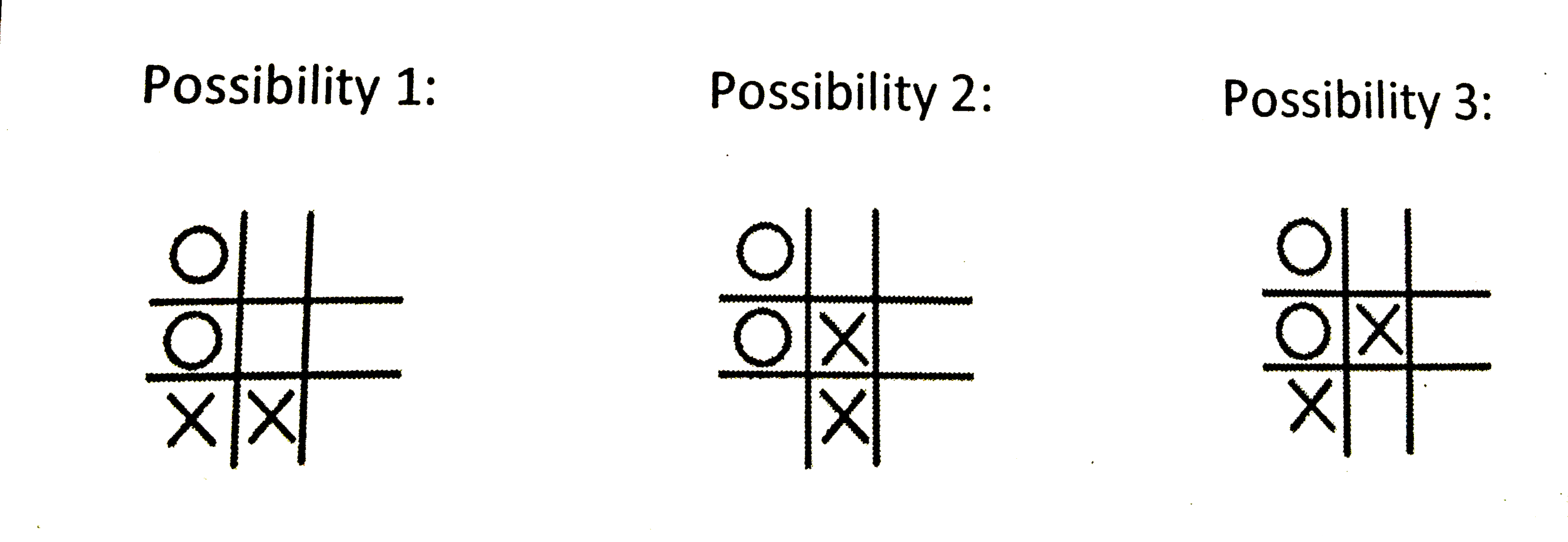


Based on the rules of the game, only possibility 3 can result in the situation after six moves. Therefore, Khaled could indeed have made the sixth move. HENCE, Khaled has made the sixth move, and Shahzia will make the seventh move and win.
Discussion
2920.

The system of equations a_1x+b_1y+c_1z=0 a_2x+b_2y+c_2z=0 a_3x+b_3y+c_3z=0 [[a_1,b_1,c_1],[a_2,b_2,c_2],[a_3,b_3,c_3]]=0

Answer»

more than TWO SOLUTIONS
ONE TRIVIAL and one NONTRIVIAL solutions
no solution
only trivial solutions

Answer :A
Discussion
2921.

Eight fair dice are thrown at random at a time. Find the probability of getting sum 24.

Answer»


Answer :`(.^(23)C_(7) - 8^(17)C_(7) + 28^(11) C_(4))/(6^(8))`
Discussion
2922.

Find the derivative of sin (sin x^(2)).

Answer»

1
2
0
None of these

ANSWER :C
Discussion
2923.

If pm 2, pm3 are the roots of ax^(4) + bx^(3) + cx^(2) + dx + e= 0then the roots of a(x + 1)^(4) + b(x + 1)^(2) + c (x + 1)^(2) + a (x + 1) + e = 0are

Answer»

1,2, -3 , -4
`-1, -2, 3 , 4 `
1, 1/21/3, 1/4
1,2,3,4

Answer :1
Discussion
2924.

Sixteen players S_(1),S_(2),…,S_(16) play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength. (a) Find the prabability that the player S_(1) is among the eight winners. (b) Find the probability that exactly one of the two players S_(1)and S_(2) is among the eight winners.

Answer»

Solution :(a) The probability of `S_(1)` to be among the eight winners is equal to the probability of `S_(1)` winning in the group, which is given by 1/2.
(b) If `S_(1) and S_(2)` are in the same pair then exactly one wins. If `S_(1) and S_(2)` are in two separate pairs, then for exactly one of `S_(1)and S_(2)` to be among the eight winners, `S_(1)` wins and `S_(2)` loses or `S_(1)` loses and `S_(2)` wins.
Now the probability of `S_(1),S_(2)` being in the same pair and one wins is
(Probability of `S_(1),S_(2)` being in the same psir) `XX` (Probability of any one winning in the pair).
And the probability of `S_(1).S_(2)` being in the same pair is `=(n(E))/(n(S))`
The number of ways 16 players are divided into 8 pairs is
`n(S)=(16!)/((2!)^(8)XX8!)`
The number of ways in which 16 persons can be divided in 8 pairs to that `S_(1)and S_(2)` are in same pair is
`n(E)=(16!)/((2!)^(7)xx7!)`
Therefore, the probability of `S_(4)and S_(2)` being in the same pair is
`((14!)/((2!)^(7)xx7!))/((16!)/((2!)^(8)xx8!))=(2!xx8)/(16xx15)=1/15`
The probability of any one winning in the pair of `S_(1),S_(2)` is P (certain event) =1.
Hence, the probability that the pair of `S_(1),S_(2)` wins is given by the sum the probability of `S_(1),S_(2)`being in two pairs separately and `S_(1)` wins, `S_(2)` loses and the probability of `S_(1),S_(2)` being in two pairs separately and `S_(1)` loses, `S_(2)` wins. It is given by
`[1-1/15]xx1/2xx1/2+[1-1/15]xx1/2xx1/2=1/2xx14/15=7/15`
Therefore, the required probability is `(1//15)+(7//15)=(8//15).`
Discussion
2925.

Let f and g be real-valued functions. If lim_(xto0)(2f(x)-g(x))/([(f(x)+7)]^(-2//3))=(7)/(4),lim_(xto0)f(x)=1andlim_(xto0)g(x)=alpha then h(x)={{:(sin(alphax),0lexle(pi)/(10)),(cos(2alphax),(pi)/(10)ltxle(pi)/(5)):} is

Answer»

continuous at `X=(pi)/(10)` only
discontinuous on `[0,(pi)/(5)]`
discontinuous at `x=(pi)/(10)`
continuous on `[0,(pi)/(5)]`

ANSWER :D
Discussion
2926.

Determine all pairs (x, y) of positive integers satisfying the equation 1 + 2^(x) + 2^(2x + 1) = y^2

Answer»


ANSWER :N= 1, 2
Discussion
2927.

The means and variance of n observations x_(1),x_(2),x_(3),…x_(n) are 0 and 5 respectively. If sum_(i=1)^(n) x_(i)^(2) = 400, then find the value of n

Answer»


ANSWER :80
Discussion
2928.

Which one of the following is a statement?

Answer»

CLOSE the door
Good EVENING sir
Bring the book
Mumbai is the CAPITAL of india

Answer :D
Discussion
2929.

Find all the number 'a' for which any rootof the equationsin 3x =a sin x +(4-2|a|)sin^(2) xis a root of the equationsin 3x + cos 2 x =1+2 sinx cos 2xand any root of the latterequation is a root of the former .

Answer»


ANSWER :`a in [1,5]`
Discussion
2930.

Find the angle between the two planes 2x + y - 2z = 5 and 3x – 6y – 2z = 7 using vector method.

Answer»


ANSWER :ANGLE `theta=cos^(-1)(4)/(21)`
Discussion
2931.

Show that the lines (x+3)/(-3) = y - 1 = (z-5)/(5) and (x+1)/(-1) = (y-2)/(2) = (z-5)/(5) are coplanar. Also find their point of intersection.

Answer»


ANSWER :(0,0,0)
Discussion
2932.

Mean of 100 items is 50 and their S.D. is 4. Find the sum of all the items and also the sum of the squares of the items.

Answer»


ANSWER :5000;2,51,600
Discussion
2933.

How many different words with two letters can be formed by suing the letters of the word JUNGLE, each containing one vowel and one consonant ?

Answer»

Solution :The word 'Jungle CONTAINS 2 vowels and 4 consonants. Each word contains one vowel and one consonant.
The NUMBER of different WORDS FORMED.
`2XX""^4P_1xx""^2P_1=2xx4xx2=16`
Discussion
2934.

The total cost function is given by C(x) = 2x^(3) - 3 . 5 x^(2) + x . The point where MC curve cuts y-axis is

Answer»

(1,0)
(0,0)
(0,1)
`(0,(1)/(6))`

ANSWER :C
Discussion
2935.

Evaluate the following integrals. int(1)/(d+e tanx)dx

Answer»


ANSWER :`(1)/(d^(2)+E^(2)){de+elog|dcosx+esinx|}+K`
Discussion
2936.

If |a|=5, |b|6 and a.b=-25, then |axxb| is equal to

Answer»

25
`6sqrt(11)`
`11sqrt5`
`5sqrt(11)`

SOLUTION :Now ,` |axxb|^2+(a.b)^2=|a|^2|b|^2`
`RARR |axxb|^2=25xx36-(25)^2`
`=25(36-25)=25xx11`
`rArr |axxb|=5sqrt(11)`
Discussion
2937.

int(9x^(3)-3x^(2)+2)/(sqrt(3x^(2)-2x+1))dx.

Answer»


Answer :`(3X^(2)+x-1)/(3)sqrt(3x^(2)-2x+1)+C.`
Discussion
2938.

If therootsofx^4 - 8x^3+ 14 x^2+ 8x- 15=0are inA.Pthen therootsare

Answer»

`-1,1,3,5`
`1,1,-3,-5`
`1,3,5,7`
`1,2,3,4`

ANSWER :A
Discussion
2939.

Let f(x) satisfy the requirements of Lagrange's mean value theorem in [0,1], f(0) = 0 and f'(x)le1-x, AA x in (0,1) then

Answer»

`F(x)gex`
`|f(x)|ge1`
`f(x)LE x (1-x)`
`f(x)le 1//4`

ANSWER :C::D
Discussion
2940.

If a+b+c=0 then the quadratic equation 3ax^2+2bx+c=0 has at least one root in

Answer»

`[1,2]`
`[0,1]`
`[-1,1]`
`[1,3]`

ANSWER :B
Discussion
2941.

Relation "parallel" in the straight line in a plane is :

Answer»

only reflexive
only symmetric
only transitive
equivalence relation

Answer :D
Discussion
2942.

Write the symmetric form of equation of the following lines : y = b, z = c

Answer»

Solution :Given LINE in UNSYMMETRICAL from is`y = b, Z = ciffy-b=0` and z - C = 0. The straight line is PARALLEL to x-axis. D.rs. Of the straight line are `lt0,0,kgt.` So the equation of the line is `(y-b)/0=(z-c)/0=x/k`
Discussion
2943.

Find the sum (sumsum)_(0leiltjlen) jxx""^(n)C_(i).

Answer»

Solution :`UNDERSET(0leiltjlen)(sumsum)j..^(N)C_(i)`
`= underset(R=0)overset(n-1)SUM.^(n)C_(r)[(r+1)+(r+2)+"...."+(n)]`
`= underset(r=0)overset(n-1)sum.^(n)C_(r)[(r+1)+(r+2)+"...."(r+(n-r))]`
`= underset(r=0)overset(n-1)sum.^(n)C_(r)(n-r)/(2)(r+1+n)`
`= 1/2 underset(r=0)overset(n)sum.^(n)C_(r) (n(n+1)-r-r^(2))`
` = 1/2[n(n+1)underset(r=0)overset(n)sum.^(n)C_(r)-underset(r=0)overset(n)sumr^(n)C_(r)-underset(r=0)overset(n)sumr^(2)..^(n)C_(r)]`
`=1/2[n(n+1).2^(n)-n underset(r=0)overset(n)sum.^(n-1)C_(r-1)-n underset(r=0)overset(n)sumr..^(n-1)C_(r-1)]`
`=1/2[n(n+1).2^(n)-n.2^(n-1)-n underset(r=0)overset(n)sum((n-1)..^(n-2)C_(r-2)+.^(n+1)C_(r-1))]`
`= 1/2[n(2n+1).2^(n-1)-n(n-1).2^(n-2)-n.2^(n-1)]`
`= n(3n+1).2^(n-3)`
Discussion
2944.

If C_(1) and C_(2) are the centres of similitude with respect to the circles x^(2) + y^(2) -14x + 6y + 33 =0 and x^(2) + y^(2) + 30x -2y + 1=0, then the equation of the circle with C_(1) C_(2) as diameter is

Answer»

`2x^(2) + 2y^(2) + 30x-33y - 17= 0`
`2x^(2) + 2y^(2) - 14x+ 9Y -13 =0`
`2x^(2) + 2y^(2) - 39X+ 14y + 74 =0`
`2x^(2) + 2y^(2) - 24x + 8y - 5 = 0`

Answer :C
Discussion
2945.

If 4c +20 ge 31, what is the least possible value of 12c +7 ?

Answer»

18
40
51
58

Solution :Subtract 20 from both sids of the INEQUALITY to find that `4c ge 11.` Multiply by `3:12c ge33.` FINALLY, add 7 to both SIDES:` 12 c + 7 ge 40.` So the least permissible VALUE for `12c +7` is 40 (B) is correct.
Discussion
2946.

The area of the triangle formed by any tangent to the hyperbolax^(2) //a^(2) -y^(2) //b^(2) =1 with its asymptotes is

Answer»

AB
abc
4 ab
`a^(2) B^(2)`

ANSWER :A
Discussion
2947.

Find the number of ways of arranging 6 red roses and 3 yellow roses of different sizes into a garland. In how many of them all the yellow roses come together.

Answer»


ANSWER :`(lfloor6xxlfloor3)/2`
Discussion
2948.

Show that the pointsA(2hati-hatj+hatk),B(hati-3hatj-5hatk),C(3hati-4j-4hatk)are vertices of a right angled triangle.

Answer»


ANSWER :HENCE, `DeltaABC` is a right ANGLED TRIANGLE.
Discussion
2949.

If the circles x ^(2) + y ^(2) - 2x - 2y -7=0 and x ^(2) + y ^(2) + 4x + 2y + k =0 cut orthogonally. If the length of the common chord of the circles is (m)/(sqrt n), then m + n is

Answer»


ANSWER :25
Discussion
2950.

int sin^(-3//2) x sin^(-1//2) (x+alpha)dx = -2 cosec alphasqrt(f(x))+c, then :

Answer»

`f(x)=TAN(x+alpha)`
`f(x)=(SINX)/(SIN(x+alpha))`
`f(x)=(sin(x+alpha))/(sinx)`
`f(x)=(tan(x+alpha))/(TANX)`.

Answer :C
Discussion