Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

1401.

The switch shown in figure is suddenly closed. Find the current through the resistor when energy dissipated in the resistor is one third of total energy dissipated in the resistor.

Answer»


SOLUTION :INITIAL ENERGY stored in conducting sphere
`U = (Q^(2))/(2C)=(Q^(2))/(8H in_(0)R)`…..(i)
when SWITCH is closed, all energy dissipated in the resistor, according to question.
Let 'q' charge on the sphere when one third energy is lost
`:. (q^(2))/(2c)=(2u)/(3),(q^(2))/(8pi(in_(0)R))=(2)/(3)(Q^(2))/(8 pi (in_(0)R))`
`:. q=sqrt((2)/(3))Q`....(ii)
HENCE point of sphere at the instant
= point dift. across resister at that instant
`:. (q)/(4pi(in_(0)R))=I.R_(0)`
`:. I =sqrt((2)/(3)).(Q)/(4 pi in_(0)R R_(0))`
Discussion
1402.

Two radioactive sources A and B of half lives-1h and 2h respectively initially contain the same number of radioactive atoms. At the end two hours, their rates of disintegration are in the ratio of :

Answer»

`1:4`
`1:3`
`1:2`
`1:1`

ANSWER :C
Discussion
1403.

The region of electromagnetic spectrum that contains Lyman an series is

Answer»

ULTRAVIOLET
INFRARED
VISIBLE
X-ray

Answer :A
Discussion
1404.

An oil drop of radiuss 2mm with density 3g/cm^-3 is held stationary under a constantvec(E) = 3.35 x 10^5 V/m in the milikan's drop experiment. What is number of excess electron that oil drop will possess (g=9.81)

Answer»


ANSWER :`N=61.60 X 10^14`
Discussion
1405.

Give the circuit symbol and truth table for OR gate.

Answer»

SOLUTION :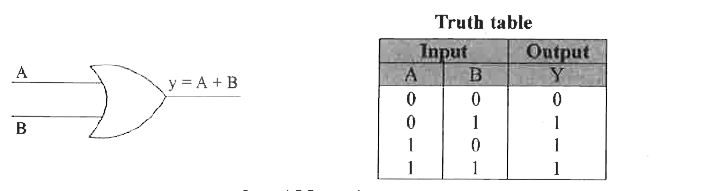
Discussion
1406.

A block of weight W is suspended from the mid-point of a rope whose ends are at the same horizontal level. The force required to straighten the rope is

Answer»

W
2W
W/2
infinitely LARGE

ANSWER :D
Discussion
1407.

An alternating current is given by the equation i = (i_1 cos omegat + i_2 sin omegat). The rms current is given by ……..

Answer»

`1/sqrt2 (i_1+i_2)`
`1/sqrt2(i_1+i_2)^2`
`1/sqrt2(i_1^2 + i_2^2)^(1/2)`
`1/2(i_1^2 + i_2^2)^(1/2)`

SOLUTION :`i=i_1 cos omegat+ i_2 SIN omegat`
`lt i^2 gt = lt (i_1 cos omegat + i_2 sin omegat)^2gt`
` lt i^2 gt = lt i_1^2 cos^2 omegat gt + lt i_2^2 sin^2 omegat gt + lt 2i, i_2 sin omegat cos omegat gt` ….(1)
But `lt i_1^2 cos^2 omegat gt = i_1^2 lt (1+cos 2 omegat)/2 gt`
`=i_1^2 (:1/2:)+(:(cos2omegat)/2:)]`
AVERAGE of `cos2omegat` one period =ZERO
`therefore lt i_1^2 cos^2 omegat gt =i_1^2/2`....(2)
Similarly `lt i_2^2 sin^2 omegat gt = i_2^2/2`...(3)
And value of `lt2sin omegat cos omegatgt` on one period =0 ...(4)
`therefore` From equation (1),(2) , (3) and (4)
`lti^2gt=i_1^2/2+i_2^2/2+0`
`=(i_1^2+i_2^2)/2`
`therefore i_(rms)=sqrt(lti^2gt)=sqrt((i_1^2+i_2^2)/2)=1/sqrt2(i_2^2+i_2^2)^(1/2)`
Discussion
1408.

The Newton's law of cooling is based on

Answer»

PLANCK's LAW
Prevost's law
Kirchhoff's law
Stefan's law of radiation

Answer :D
Discussion
1409.

A hot body is allowed to cool. The surrounding temperature is constant at 30^(@)C. This takes time t_(1) to cool from 70^(@)C" to "68^(@)C and time t_(2) to cool from 60^(@)C" to "59.5^(@)C. Then

Answer»

`t_(2)=t_(1)`
`t_(2)=2t_(1)`
`t_(2)=(1)/(2)t_(1)`
`t_(2)=4t_(1)`

Solution :By Newton.s law of cooling
`(dT)/(dt) =ALPHA (T-T_(0))`
`therefore (2)/(t_(1)) =alpha (90-30)=60 alpha" ….(i)"`
and `(0.5)/(t_(2))=alpha (60-30)=30 alpha" …..(ii)"`
So, correct CHOICE is (b).
Discussion
1410.

In a amplitude modulation :

Answer»

Only the AMPLITUDE is CHANGED but frequency REMAINS same
Both the amplitude and frequency change equally
Both the amplitude and frequency change unequally
None of the above

Answer :A
Discussion
1411.

A balloon from rest accelerates uniformly upward with 'a' ms^(-2) ,for t seconds of time .A stone is released from the ballon .Now ,read the following statement to pick the right ones. a) The stone's initial velocity is zero, relative to balloon b)The stone's initial velocity is nonzero, relative to earth c)The time taken to reach the ground from the balloon's frame of refrence is inversely proportional to sqrt((a+g)). d)The time take to reach the ground from earth,s frame of refrence is directly proportional to sqrt((a+g))

Answer»

a,B,C
a,c,d
a,b,d
a,c

Answer :A
Discussion
1412.

To produce N - type crystal Ge or Si may be doped with a substance that is :

Answer»

DIVALENT
TRIVALENT
TETRAVALENT
pentavalent.

Answer :D
Discussion
1413.

The scalar product of two vector a = 3vechati-4vechatj+vechatk andvecb=-2vechati+ vechatj +3vechatkis

Answer»

-7
20
`-20`
`-25`

ANSWER :D
Discussion
1414.

An electric dipole consists of two opposite charges of magnitude 1mu C separated by a distance of 2cm. The dipole is placed in an electric field 10^(-5) Vm^(-1). The maximum torque does the field exert on the dipole is

Answer»

`10^(-3)NM`
`2 xx 10^(-13)Nm`
`3 xx 10^(-3)Nm`
`4 xx 10^(-3) Nm`

Answer :B
Discussion
1415.

In the circuit given, the current through the Zener diode is

Answer»

10 mA
6.67 mA
5 mA
3.33 mA

Solution :The VOLTAGE drop across `R_(2)` is
`V_(R_(2))=V_(Z )=10V`
The current through `R_(2)` is
`I_(R_(2))=(V_(R_(2)))/(R_(2))=(10V)/(1500Omega)`
`=0.667xx10^(-2)A`
`=6.67xx10^(-3)A=6.67mA`
The voltage drop across `R_(1)` is `V_(R_(1))=15V-V_(R_(2))=15V-10V=5V`

The current through `R_(1)` is
`I_(R_(1))=(V_(R_(1)))/(R_(1))=(5)/(500OMEGA)=10^(-2)A=10xx10^(-3)A=10mA`
The currentthrough the zener diode is
`I_(Z)=I_(R_(1))-I_(R_(2))=(10.6.67)mA=3.33 mA`
Discussion
1416.

A deutron strikes ""_6O^(16) nucleus with the subsequent emission of an alpha-particle. Find the atomic number, mass number and chemical name of the element so produced.

Answer»

SOLUTION :The nuclear REACTION may be expressed as under
`""_8O^(16) +""_1H^2 to ""_zX^A+""_2He^4(ALPHA-"particle")`
Law of conservation of charge 8+1=Z+2 `rArr Z=7`
The atomic number of the ELEMENT is 7 `rArr` element is nitrogen
Law of conservation of mass number `16+2 =A+4 rArr A=14`
`""_zX^A=""_7N^(14)`
Discussion
1417.

In the circuit shown in figure, capacitor A has capacitance C_(1)=2muF when filled with a di-electric slab of dielectric constant k=2. Capacitors B and C are air capacitors and have capacitances C_(2)=3muF and C_(3)=6muF, respectively. A is charged by closing switch S_(1) alone (a) Calculate energy supplied by battery during process of charging. Switch S_(1) is now opened and S_(2) is closed. (b) Calculate charge on B and energy stored in the system when electrical equilibrium is attained. Now switch S_(2) is also opened, slab of A is removed. Another di-electric slab of K=2, which can just fill the space in B, is inserted into it and then switch S_(2) alone is closed. (c) Calculate by how many times electric field in B is increased. Calculate also, loss. of energy during redistribution of charge.

Answer»


ANSWER :(a) `0.0648J`, ENERGY stored in capacitor is `1/2CV^(2)`, but energy SUPPLIED by BATTERY is `CV^(2)`; (B) `180muC, 0.0162J`; © `0.75, 0.0054J`
Discussion
1418.

The phase difference between current and voltage for L-C-R A.C. series circuit is …….

Answer»

between 0 to `PM PI/2`
`pi/2`
`pi`
between 0 and `pi/2`

ANSWER :A
Discussion
1419.

If the identical cells each having an emf of 20 V are connected in Parallel, then the emf of the combinations is

Answer»

2 V
200 V
20 V
10 V

Answer :C
Discussion
1420.

If a very long thin wire is bent as shown carries a current i, then find B_("net") at the centre O of semicircular arc of radius r. which is in xy plane semi infinite wires connecting the arc in xz plane and also find the magnetic induction in vectorial from

Answer»

Solution :`B_(1)=B_(3)=(mu_(0))/(4pi)I/r(-hatj)`
`B_(2)=(mu_(0)1/2I)/(2r)=(mu_(0)I)/(4r)(-HATK)`
`B_("NET")=(-mu_(0)I)/(4r)(2/pihatj+hatk)`
Discussion
1421.

Answer questions on the basis of your understanding of the followingparagraph and the related studied concept. Electric flux, in general , through any surface is defined as per relation: phi_E= int oversetto E. oversetto (ds), whereintegration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. Whenflux through a closed surface is required we use a small circular sign on the integrationsymbol. Thus flux over a closed surface oint E= oint oversetto E. oversetto (ds) .it is customary to take the outward normal as positive in this case. A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by in_0 . Mathematically oint oversetto (E) . oversetto (ds) =(1)/( in_0)[q_(en) ], where q_(cn)is the net charge enclosedwithin the surface. It is possible to derive Gauss' lawfrom Coulomb's laws. Gauss' lawcan be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations. What is the electricalflux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?

Answer»

`(q)/(in_0) `
` (2Q)/(in_0) `
` (q)/(8in_0) `
` (q)/(in_0). 6a^(2) `

SOLUTION :Elight identical cubes are arranged so that a closed SURFACE is formed with a given charges .q. at the CENTRE of that closed surface. The closed surfaceis a big CUBE of side .2a..
Discussion
1422.

In the circuit shown in figure, if the charge on capacitor C_(2) in steady state is (10x)/3 muC, then find value of x.

Answer»


Solution :During the steady state the capacitors are fully charged and will behave like open circuit. So the CURRENT will FLOW outer loop only. The current in the outer loop will be `=30/10=3` Amp. in clockwise direction. Charge distribution on the plates of capacitors are as shown in figure.
Applying KVL in loop -I
`q/2+(q_(1))/2-15=0impliesq+q_(1)=30`.........(1)
Applying KVL in loop -II
`(q-q_(1))/10-6+10-(q_(1))/2=0`............(2)
On SOLVING equation (1) and (2) we get `q_(1)=10MU C`
Discussion
1423.

Answer questions on the basis of your understanding of the followingparagraph and the related studied concept. Electric flux, in general , through any surface is defined as per relation: phi_E= int oversetto E. oversetto (ds), whereintegration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. Whenflux through a closed surface is required we use a small circular sign on the integrationsymbol. Thus flux over a closed surface oint E= oint oversetto E. oversetto (ds) .it is customary to take the outward normal as positive in this case. A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by in_0 . Mathematically oint oversetto (E) . oversetto (ds) =(1)/( in_0)[q_(en) ], where q_(cn)is the net charge enclosedwithin the surface. It is possible to derive Gauss' lawfrom Coulomb's laws. Gauss' lawcan be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations. A square surface of side L m is in the plane ofpaper. A uniform electric fieldoversetto EV m ^(-1), also in the plane of the paper, is limited only to the lower half of the square surface as shown in adjoining figure. The electric flux, in SI units, associated with the surfer is : (##U_LIK_SP_PHY_XII_C01_E03_012_Q01.png" width="80%">

Answer»

zero
`EL^(2) `
` (EL^(2))/( 2 in _0) `
` (EL^(2))/(2) `

SOLUTION :SINCE electric FIELD ` oversetto E ` lies PARALLEL to the surface area , `oversetto Eand overesetto S ` are mutuallyperpendicular to each other and hence net electric flux will be zero.
Discussion
1424.

Answer questions on the basis of your understanding of the followingparagraph and the related studied concept. Electric flux, in general , through any surface is defined as per relation: phi_E= int oversetto E. oversetto (ds), whereintegration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. Whenflux through a closed surface is required we use a small circular sign on the integrationsymbol. Thus flux over a closed surface oint E= oint oversetto E. oversetto (ds) .it is customary to take the outward normal as positive in this case. A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by in_0 . Mathematically oint oversetto (E) . oversetto (ds) =(1)/( in_0)[q_(en) ], where q_(cn)is the net charge enclosedwithin the surface. It is possible to derive Gauss' lawfrom Coulomb's laws. Gauss' lawcan be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations. A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.

Answer»

be DOUBLED
INCREASES four times
be reduced to half.
remain the same.

SOLUTION :For give enclosed charges net ELECTRIC flux is independent of the surface area.
Discussion
1425.

The solids having high conductivity is called-?

Answer»


ANSWER :CONDUCTORS
Discussion
1426.

Express angular width of central maximum in terms of wavelength.

Answer»

SOLUTION :For a diffraction minima `n lambda=d sin theta`, to find the WIDTH of the central MAXIMUM, put `n=1` then`sin theta=(lambda)/(d):theta=sin^(-1)((lambda)/(d))`. Here `'theta'` is semi angular width.
For a TOTAL angular width `theta'=20=2 sin^(-1)((lambda)/(d))`
Discussion
1427.

A message signal of freuency omega_(m) is superposed on a carrier wave of frequency omega_(c) to get an amplititude modulated wave (AM). The frequency of the AM wave will be

Answer»

`omega_(m)`
`omega_(c)`
`(omega_(c)+omega_(m))/(2)`
`(omega_(c)-omega_(m))/(2)`

SOLUTION :In amplitude modulation, the frequency of modulated wave is equal to the frequency of CARRIER wave.
Discussion
1428.

Results of calculations for four difforent designs of a fusion reactor using D-D reaction are given below. Which of these is most promising based on Lawson criterion ?

Answer»

Deuteron density `=2.0 xx 10^(12)CM^(-3)", CONFINEMENT time "=5.0 xx 10^(-3)s.`
Deuteron density `=8.0 xx 10^(14)cm^(-3)," confinement time "=9.0 xx 10^(-1)s`.
Deuteron density `=4.0 xx 10^(23)cm^(-3)", confinement time "=1.0 xx 10^(-11)s.`
Deuteron density `=1.0 xx 10^(24)cm^(-3)" confinement time "=4.0 xx 10^(-12)s`.

Solution :The product of the deuteron density and confinement time `t_(0)` should be GREATER than Lawson criteria,
`5 xx 10^(14) s cm^(-3)`
DEUTRON density `=8.0 xx 10^(+14) cm^(-3)`
confinement time `=9.0 xx 10^(-1)s`
Lawson criteria `=8.0 xx 10^(+14) xx9.0 xx 10^(-1)`
`=7.2 xx 10^(+14)`
It is not enough if the density is very high but the confinement time also should be high enough for the reaction.
Discussion
1429.

A force of 10 N inclined to the horizontal at an angle of 60^(@) acts on a body of mass 2 kg. If the body can move in horizontal direction only find its acceleration.

Answer»

`2.5 m//sec^(2)`
`5.5 m//sec^(2)`
`4.5 m//sec^(2)`
`3.5 m//sec^(2)`

ANSWER :A
Discussion
1430.

Television broadcast is done by space wave mode of propagation.What is the difference between sky wave and space wave modes of propagation?

Answer»

Solution :In SKY wave the SIGNAL is reflected from the lonosphere and RECEIVED. In spacewave signal is di rectly received by the RECEIVING ANTENNA.
Discussion
1431.

A metal plate 100cm^2 in area rests horizontally ona layer of oil 2 mm thick.A force of 0.1 N applied to the plate horizontally keeps it moving with a uniform speed of 2cm/s . Find the viscosity of oil.

Answer»

Solution :Since the metal plate is moving uniformly the applied FORCE just overcomes the drag
From F = `eta A (DV)/(dy),eta = (F)/(A(dv)/(dy))` = `(0.1)/(100 xx 10^-4) xx (2 xx 10^-2)/(2 xx 10^-3) = 1Ns/m^2`
Discussion
1432.

The figure shows a portion of a circuit. Resistor are known and indicated on diagram and voltmeter are identical. If voltmeters v_(1) and v_(2) reads 7.5v and 5v respecticely then reading of v_(3)

Answer»

`0v`
`10v`
`2.5v`
`3.0v`

Solution :since voltmeter are indentical

`(I_(1))/(I_(2))=(3)/(2)` LET `I_(2)=x I_(1)=(3)/(2)x`
`9xx(3)/(2)x-14x+5-7.5=0`
`x=-5.0A=I_(2)`
`-7.5A=I_(1)`
`(27x-28x)/(2)=2.5`
HENCE RESISTANCE of Voltemeter is `1Omega`
`25I_(3) = -7.5xx9 = -75`
`I_(3) = -3A`
Hence `V_(3)=3.0V`
Discussion
1433.

What is the magnitude of electric potential of the Earth ?

Answer»

Solution :Zero. (The reference potential can be SELECTED as zero INSPITE of the fact that ELECTRIC potential of the EARTH is NEGATIVE ) .
Discussion
1434.

A man can jump vertically through a height 1.5 m on earth. The maximum radius of the planet of the same density as that of earth from whose gravitational field he can escape by jumping is (R_(e )=6400 km) :

Answer»

6 KM
7 km
3.1 km
5 km.

Solution :Here square of velocity of man who can jump 1.5 m
`=V^(2)=2gh=2xx(GM_(e ))/(R_(e)^(2)xx H)`
Square of escape velocity from planet is `v_(e )^(2)=(2GM_(p))/(R_(p))`.
Now `v_(e)^(2)=v^(2) therefore R_(p)=sqrt(R_(e )xxh)` if we SUBSTITUTE for velocities `v_(e )` and v and masses in terms of volume `xx` density.
Then `R_(p)=sqrt(6400xx10^(3)xx1.5)=3.1xx10^(3)m or =3.1km`.
Correct choice is (c ).
Discussion
1435.

What is Huygens's wave theory?

Answer»

SOLUTION :Light is a longitudinal WAVE that TRAVELLED through an invisible substance CALLED .ether.
Discussion
1436.

Two charged particles are placed at a distance of 1.0cm apart. What is the minimum possible magnitude of electrostatic force acting on each charge.

Answer»

`25 XX 10^(-24)N`
`23 xx 10^(-24)N`
`2.3 xx 10^(-24)` DYNE
`2.3 xx 10^(-24)N`

Answer :D
Discussion
1437.

Two charges of equal magnitude and at a distance 'r' exert a force'F' on each other. If the charge are halved and the distance between them is doubled, then the new force between them is

Answer»

F/8
4F
F/16
F/4

Answer :C
Discussion
1438.

An electric dipole moment oversettoP is lying along uniform electric field oversettoE. The work done in rotating the dipole by 90^@ is:

Answer»

PE
`SQRT(2PE)`
`PE/2`
2PE

Answer :A
Discussion
1439.

Induced e.m.f is also called back e.m.f. why?

Answer»

SOLUTION :It is because e.m.f. ALWAYS OPPOSES any CHANGE in APPLIED e.m.f.
Discussion
1440.

Calculate the earth's total induction (B-vector) at a place where the H-vector of the maagnetic field along the horizontal is 30Am^(-1) .

Answer»


ANSWER :`4.9xx10^(-5)T`
Discussion
1441.

q_1, q_2, q_3and q_4 are point charges located at points as shown in the figure and S is a spherical Gaussian surface of radius R. Which of the s following is true according to the Gauss's law

Answer»

`OINT (VEC(E_1) + vec(E_2) + vec(E_3)) .d vec(A) = (q_1 + q_2 + q_3)/(2epsilon_0)` 
`oint (vec(E_1) + vec(E_2) + vec(E_3)) .d vec(A) = ((q_1 + q_2 + q_3))/(epsilon_0)` 
`oint (vec(E_1) + vec(E_2) + vec(E_3)) .d vec(A) = ((q_1 + q_2 + q_3 + q_4))/(epsilon_0)` 
NONE of the above

Answer :B
Discussion
1442.

A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60°, and one of the fields has a magnitude of 1.2 xx 10^(-2) T. If the dipole comes to stable equilibrium at an angle of 15° with this field, what is the magnitude of theother field?

Answer»

Solution :Here angle between `overset(to) (B_1) and overset(to)(B_2)` is `theta =60^@`.
SUPPOSE, `overset(to)(B_R) = overset(to) (B_1) + overset(to) (B_2)`
Now, as per the statement if `B_(1) = 0.012 T`, then angle between `overset(to)(m) ("or" B_(R) ) and overset(to)(B_1)` will be `alpha= 15^(@)`. (Here ,` overset(to)(m)` is the dipole MOMENT of given magnetic dipole).
For stable equilibrium, we know that `overset(to) (m) || overset(to) (B_R)` .
See the figure given below. Here,
`angle SPR = angle SPQ - angle RPQ`
`therefore beta = 60^@ - 15^(@) = 45^(@)`

When magnetic dipole comes under stable equilibrium, torques exerted on it by `B_(1) and B_(2)` are equal in magnitude and opposite in direction. Hence,
`tau_(1) (XX) = tau_(2) (.)`
`mB_(1)sin alpha = mB_(2) sin beta`
`therefore B_(2) = (B_(1) sin alpha )/( sin beta) = ((0.012)sin (15^(@ ) ) )/( sin (45^(@) ) )= ((0.012 )(0.2588) )/( (0.7071) )`
`therefore B_(2) = 0.004392` T
Discussion
1443.

The vibrations of 4 air columns are as shown in the fig. the ratio of the frequencies A, B , C , D is :

Answer»

`12 : 6 : 3 : 4 `
`1: 2 : 4 : 3 `
`4 : 2 : 3: 1`
`6 : 2 : 3 : 4 `

Answer :B
Discussion
1444.

Which of the following is involved in the extraction of Ag from argentite ?

Answer»

`[Ag(NH_(3))_(2)]^(+)`
`[Ag(SCN)_(4)]^(3+)`
`[Ag(CN)_(2)]^(-)`
`[AgCl_(2)]^(-)`

Solution :`Ag_(2)S+4NaCNoverset("AIR")(hArr)2Na[Ag(CN)_(2)] + Na_(2)S`
Discussion
1445.

When ultraviolet rays fall on a metal plate then photoelectric effect does not occur , it occurs by

Answer»

infrared rays
X-rays
RADIOWAVE
Light wave

ANSWER :B
Discussion
1446.

The ionization of H-atom is :

Answer»

13.6 J
13.6 eV
1 eV
10.2 eV

Answer :B
Discussion
1447.

A stationary positive muon disintegrated into a positron and two neutrions. Find the greatest possible kinetic energy of the positron.

Answer»

Solution :The REACTION is
`mu^(+)rarre^(+)+barv_(e )+barv_(mu)`
The neutrinoes are massless. The positron will carry largest MOMENTUM if both neutriones `(v_(e )&bar(v)_(mu))` move in the same direction in the REST frame of the noun. Then the final product is effectively a two body system and we get from problem (295)
`(T_(e^(+)))_(max)=((m_(mu)-m_(e ))^(2))/(2m_(mu))`
SUBSTITUTION gives `(T_(e^(+)))_(max)= 52.35MeV`
Discussion
1448.

A and B are two identical point sized metal spheres each holding the same charge .q.. These two are separated by certain distance and the mutual electrostatic force between them is F. If a third identical uncharged sphere .C. is touched with A and kept exactly at the midpoint of line joining A and B, what is the resulting force on C and its direction?

Answer»

SOLUTION :FORCE between two charges

When third identical uncharged sphere TOUCHED with A and placed at the mid point of AB, then

`F_("net") = F_(1) - F_(2)`
`K ((q^(2)//4))/(r^(2)//4)- K ((q^(2)//2))/(r^(2)//4) = (Kq^(2))/(r^(2))-2.(Kq^(2))/(r^(2))= F- 2F`
`F_("net")= -F` i.e., resultant force is F towards A
Discussion
1449.

What are optoelectronic devices? Give the names of such major devices.

Answer»

Solution :OPTOELECTRONIC junction is the device in which the photons (PHOTO excitation) generates the CARRIERS due to the photons.
Optoelectronic device are as follows:
(1) Photodiodes used for detecting optical signal (photodetectors).
(2) Light emitting diodes (LED) which convert electrical energy into light.
(3) Photovoltaic DEVICES which convert optical radiation into electricity (SOLAR cell).
Discussion
1450.

A rod of mass m can rotate without friction about axis sliding (also without friction) along a conducting ring of radius b arranged in a vertical plane as shown in the . The entire arrengement is placed in a uniform magnetic field with the inducetion B perpendicular to the plane of the ring. The axis and the conductor are connected to teh terminals of a current source. Determine (a) according to which law current I flowing in the rod must vary for the rod to rotate at a constant angular speed. Being to measure the time from the instant when the rod is in its right-hand horizontal position. Consider the current to be positive when it flows from the axis of rotation toward the ring. (b) what emf E of the source must be applied to maintain the required current? Consider the total resistance of the circuit to be constant and equal to R. Disergard the inductance of teh circuit.

Answer»


SOLUTION :(a) `tau_(B) = F_(B) xx (b)/(2)rarr tau_(B) = IbB xx (b)/(2) = IB(b^(2))/(2)`
`tau_(net) = 0 `rarr` MG COS THETA xx (b)/(2) = (IBb^(2))/(2)`
`rarr` `mg cos theta = IBb`
`theta = omegat`
`rarr` `I = (mg cos omegat)/(Bb)`

(b) `((E - E_(i nd)))/(R) = I`, `E = E_(i nd). + IR`
`rarr` `E = (Bomegab^(2))/(2) + (mg R cos omegat)/(Bb)`
Discussion