Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1751. |
The intial configuration of the system is as shown in the figure. The string and the pulley are light. The bob is released and the string starts wrapping around the pulley. (The pulley is held in place by a force applied at the centre) Find the rate r at which the length of the string warpped around the pulley increaes (as a function of theta). |
|
Answer» `R=(R)/((l-Rtheta))SQRT([2G(l-Rtheta)sin theta])` |
|
| 1752. |
Two charges 4 xx 10^(-9) C and -16 xx 10^(-9) C are separated by a distance 20 cm in air. The position of the neutral point from the small charge is |
|
Answer» 40/3cm |
|
| 1753. |
A magnet of magnetic dipole moment 10 Am^2 is freely suspended in a uniform magnetic field of strength 5 T. The work done in rotating the magnet through an angle 60^@ is given by : |
|
Answer» 5 J |
|
| 1754. |
Two wires are made of the same material and has the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by ax on applying force F, how much force is needed to stretch wire 2 by the same amount ? |
|
Answer» 4F For wire 1, `Y=(FL)/(ADeltaX)` ..(1) For wire 2 `Y=(F_(l)xxl/3)/(3ADeltax)` …(2) From 1 and 2 `(Fl)/(ADeltax)=(F^(l)l)/(9ADeltax)` `F_(1)=9F` So Correct choice is (C). |
|
| 1755. |
At a point on the two-slit interference pattern obtained using a source of light of wavelength 6000Å, the pathdifference is 4.2 mu m. Is the point bright or dark? |
|
Answer» Solution :Data: Path DIFFERENCE, `Delta= 4.2 xx 10^(-6) m, lambda = 6000 Å= 6 xx 10^(-7)`m Let p be an integer such that `p(lambda/2)= Delta`. `therefore p=(2Delta)/lambda = (2 xx 4.2 xx 10^(-6))/(6 xx 10^(-7)) = (8.4 xx 10)/6` `= 84/6 = 14` Since p is an even integer, the point MUST be BRIGHT. |
|
| 1756. |
A ray of light suffers a minimum deviation when incident on a equilateral prism of refractive index sqrt2 . The angle of incidence is |
|
Answer» `30^(@)` `sqrt(2)=((sin(60+D))/(2))/(sin""(60)/(2))` `sqrt(2)=(sin((60+D)/(2)))/(sin30)` `sqrt(2)xx(1)/(2)=sin((60+D)/(2))` `=(60+D)/(2)=45`. `60+D=90` `D=30` `2i=A+D` `2i=60+30` `i=(90)/(2)` `i=45^(@)` |
|
| 1757. |
A magnet is suspended from a spring and while it oscillates, the magnet moves in and out of a coil which is connected to a galvanometer G. Then, as the magnet oscillates |
|
Answer» `G` shows DEFLECTION to the LEFT and RIGHT with CONSTANT amplitude |
|
| 1758. |
The x rays shown are produced when 35.0 ke V electrons strike a molybdenum (Z=42) target. If the accelerating potential is maintained at this value but a silver (Z=47) target is used instead, what values of (a) lambda_(min), (b) the wavelength of the K_(alpha) line, and (c ) the wavelength of the K_(beta) line result? The K, L, and M atomic x-ray levels for silver are 25.51, 3.56, and 0.53 keV. |
| Answer» SOLUTION :(a) 5.4 PM, (B) 56.5 pm, (C ) 49.6 pm | |
| 1759. |
In example (8), if rectangular loop is replaced by Circular loop then will the induced emf be of constant magnitude or not while entering the magnetic field? |
| Answer» SOLUTION :VARIABLE | |
| 1760. |
If a current I = 5sin (omega t - pi/2) flows in an a.c. circuit on applying a potential V = 310 sin omegat, then the power consumption P in the circuit will be |
|
Answer» `P = 310 xx 5 W` |
|
| 1761. |
Using constraint equations find the relation between a_1 and a_2 |
|
Answer» SOLUTION :Point 1,2,3 and 4 are MOVABLE. Let their dis-placement from a fixed line be ` x_1 , x_2 , x_3 and x_4` `x_1 + x_3 =l_1` `(x_1 - x_3 )+ ( x_4- x_3) =l_2` ` (x_1 - x_4 ) + (x_2 - x_4) = l_3` On double DIFFERENTIATING with respect to TIME , we will GET following three constraint relations : ` a_1 + a_3 =0` ....... (i) `a_1 + a_4 - 2a_3 =0`........ (ii) `a_1 + a_2 - 2a_4 =0`............ (iii) SolvingEqs. (i) ,(ii) and (iii) , we get ` a_2=-7a_1 ` Which is the desired relation between ` a_1 and a_2` 
|
|
| 1762. |
The magnetic field strength B at the point between the capacitor plates is indicated in figure. B in terms of the rate of charge of the electric field strength, i.e., dE/dt between the plates is equal to |
|
Answer» `(MU _(0))/( 2pi r ) (dE)/(dt)` `= (mu _(0))/( 2pi r ) epsi _(0) (d )/(dt) (E pi r ^(2)) = (mu_(0) epsi _(0) r )/(2) (dE)/(dt)` |
|
| 1763. |
Interference can be observed in wave motions under suitable conditions. Consider only interference in ligth and second waves, between two waves at a time. |
|
Answer» |
|
| 1764. |
When was the inauguration day? |
|
Answer» 44326 |
|
| 1765. |
A circular coil of 30 turns and radius 8.0 cm carrying a current or 6.0 A is suspend vertically in a uniform horizontal magnetic field of lines make an angle of 60^@ with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning. b. Whould your answer change, if the circular coil in (a) were replaced by a plannar coil of some irregular shape that encloses the same area ? (All other particulars are also unaltered. ) |
|
Answer» Solution :N=30, `r=8 xx 10^(-2) m, I = 6A, B =1 T theta = 60^(@)` `tau = "BANI" sin 60^(@) =1 xx pi xx (8 xx 10^(-2))^2 xx 30 xx 6 xx SQRT(3)/2 = 3.1Nm` b. No CHANGE.`because vec tau = NI(vec A xx vec B)` |
|
| 1766. |
For transistor action: (1) Base, emitter and collector regions should have similar size and doping concentrations. (2)The base region must be very thin and lightly doped. ( 3) The emitter-base junction is forward biased and base-collector junction is reverse biased. (4) Both the emitter-base junction as well as the base-collector junction are forward biased. Which one of the following pairs of statements is correct? |
|
Answer» (1) and (4) |
|
| 1767. |
Which of the following pair of electric and magnetic fields represents the source of light? |
|
Answer» `vecB=B_0sin(omegat-kx)hatj` and `vecE=E_0 SIN (omegat-kz)hatk` |
|
| 1768. |
For television broadcasting, the frequency employed is normally: |
| Answer» Answer :A | |
| 1769. |
In Rutherford scattering experiment, what will be correct angle for alpha- scattering for an impact parameter b=0 ? |
|
Answer» `90^(@)` |
|
| 1770. |
The aperture of a telescope is of 1m diameter and wavelength of light incident on the paerture is 5500 A^(@). The angular limit of resolution of the telescope is |
|
Answer» `6.71 XX 10^(-7)` radian |
|
| 1771. |
Core of electromagente are made of ferromagnetic material which has |
|
Answer» HIGH PERMEABILITY and highretentivity |
|
| 1772. |
n object of mass 3 kg is at rest. A force vec(F)=6hat(i)t^(2) + 4hat(j)tis applied, then velocity of the object at t = 3 second is : |
|
Answer» `18hat(i) + 3hat(j)` `dv=6/3hati t^(2)dt + 4/3 hatjt dt` `v=2hati[t^(3)/3]_(0)^(3) + 4/3hatj[t^(2)/2]_(3)^(0)` `2hati xx27/3 + 4/3 hatj xx 9/2 = 18hati + 6hatj` |
|
| 1773. |
How many solid spherical balls of radius 2cm and b are constants. If f(2)=1" and "f(-3)=11, |
|
Answer» 4 |
|
| 1774. |
What is the nature of image formed by a concave mirror at infinity ? |
| Answer» SOLUTION :REAL, INVERTED and EXTREMELY DIMINISHED. | |
| 1775. |
If "^amu_g = 3/2 and "^amu_omega = 4/3 therefore "^omegamu_g = ? |
|
Answer» 8/9 |
|
| 1776. |
A convex driving mirror of focal length 20cm, is fitted in a motor car. If the second car 2m broad and 1.6m hight is 6m away from first car and overtake the first car at a relative speed of 15m//s, then how fast will the image he moving? |
|
Answer» `0.016m//s` Differentiating w.r.t we get `0=-1/(v^(2))(DV)/(DT)-1/(u^(2))(du)/(dt)` `(du)/(dt)=-(v^(2))/(u^(2))(du)/(dt)` But `(du)/(dt)=15m//s` Now `1/v=(1/20+1/600)` `:.v=600-31cm` and `v/u=(600/31)/600=1/31` `:.` SPEED of image `=(dv)/(dt)=-(1/31)^(2)xx16=0.016m//s` |
|
| 1777. |
A metallic conductor at 10^(@)C connected in the left gap of meter bridge gives balancing length 40 cm. When the conductor is at 60^(@)C, the balancing point shifts by ---cm, (temperature coefficient of resistance of the material of the wire is (1//220)//""^(@)C) |
|
Answer» 4.8 |
|
| 1778. |
In the following nuclear fission reaction, N is the number of neutrons released. What is the value of N ?_92U^235+_0n^1to_38Sr^94+_54Xe^140+N |
| Answer» SOLUTION :2 NEUTRONS | |
| 1779. |
(a) Find magnetic field inside a long solenoid, carrying current (1//pi) A and having number of turns per unit length 10. Also calculate magnetic field at ends. (b) A long solenoid is fabricated by closely winding a wire of diameter 10 mm over a cylinderical non-magnetic frame so that the successive turns nearly touch each other. Find magnetic field at the centre and ends of solenoid if it carriers a current (4//pi) A? (c) A single-layer coil (solenoid) has length l and cross-section radius R. The number of turns per unit length is equal to n. Find the magnetic induction at the centre of the coil when a current i flows through it. (d) A solenoid of length 0.4 m anddiameter 0.6 m consists of a single layer of 1000 turns of the fine wire carrying a current of 5 mA. Calculate the magnetic field on the axis at the middle and at the ends of the solenoid. |
|
Answer» Solution :(a) `i=1/piA, n=10` `B_(centre)=mu_(0)ni=(4pixx10^(-7))(10)(1/pi)=4xx10^(-6) T` `B_(end)=1/2 mu_(0) ni=2xx10^(-6) T` (b) 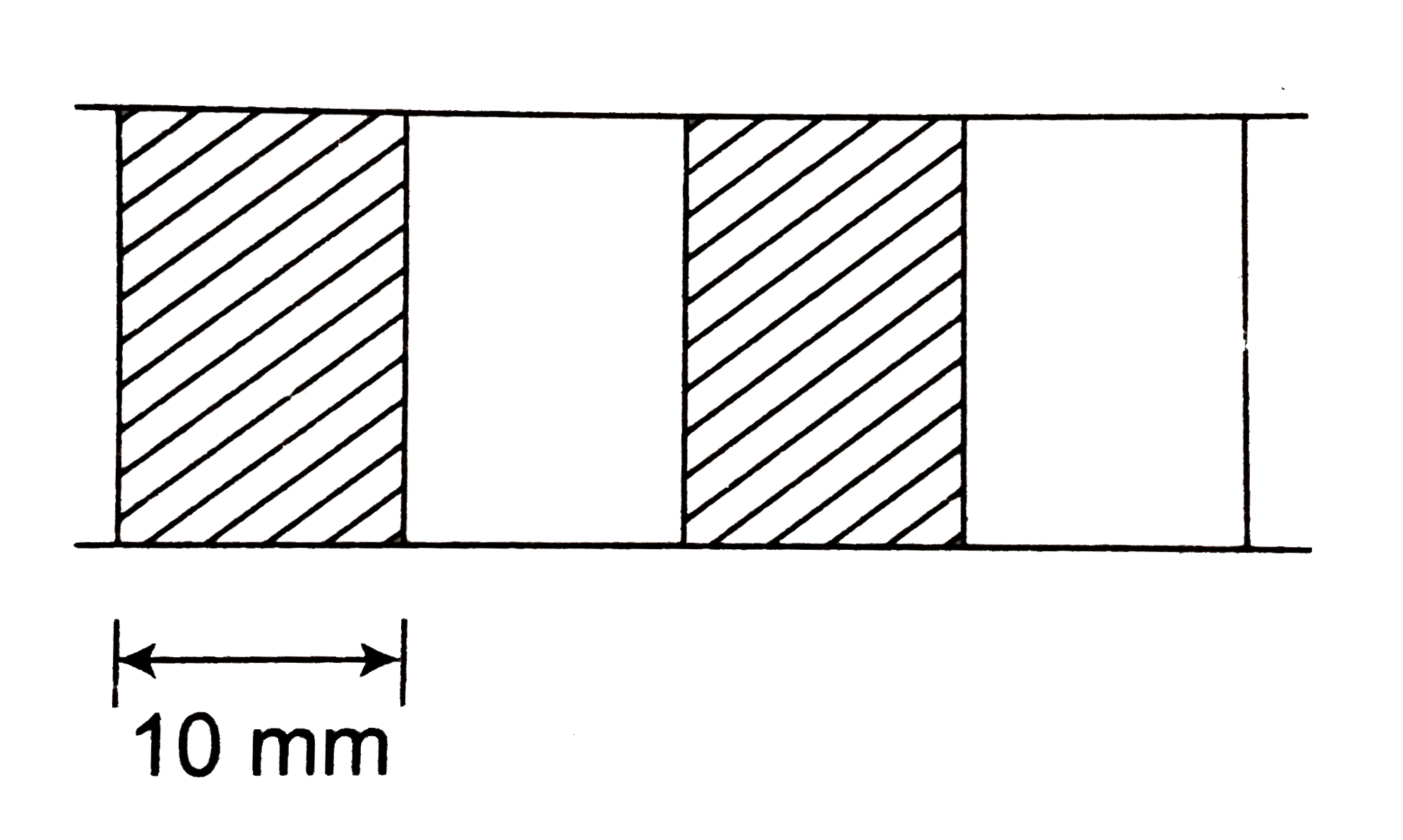 Number of TURNS in `10 mm` length `=1` Number of turns in `1m` length `n=100` `i=4/(pi) A` `B_(centre)=mu_(0)ni=(4pixx10^(-7))(100)(4/pi)` `=16xx10^(-5)T` `B_(end)=1/2 mu_(0) ni =8xx10^(-5) T` (C) 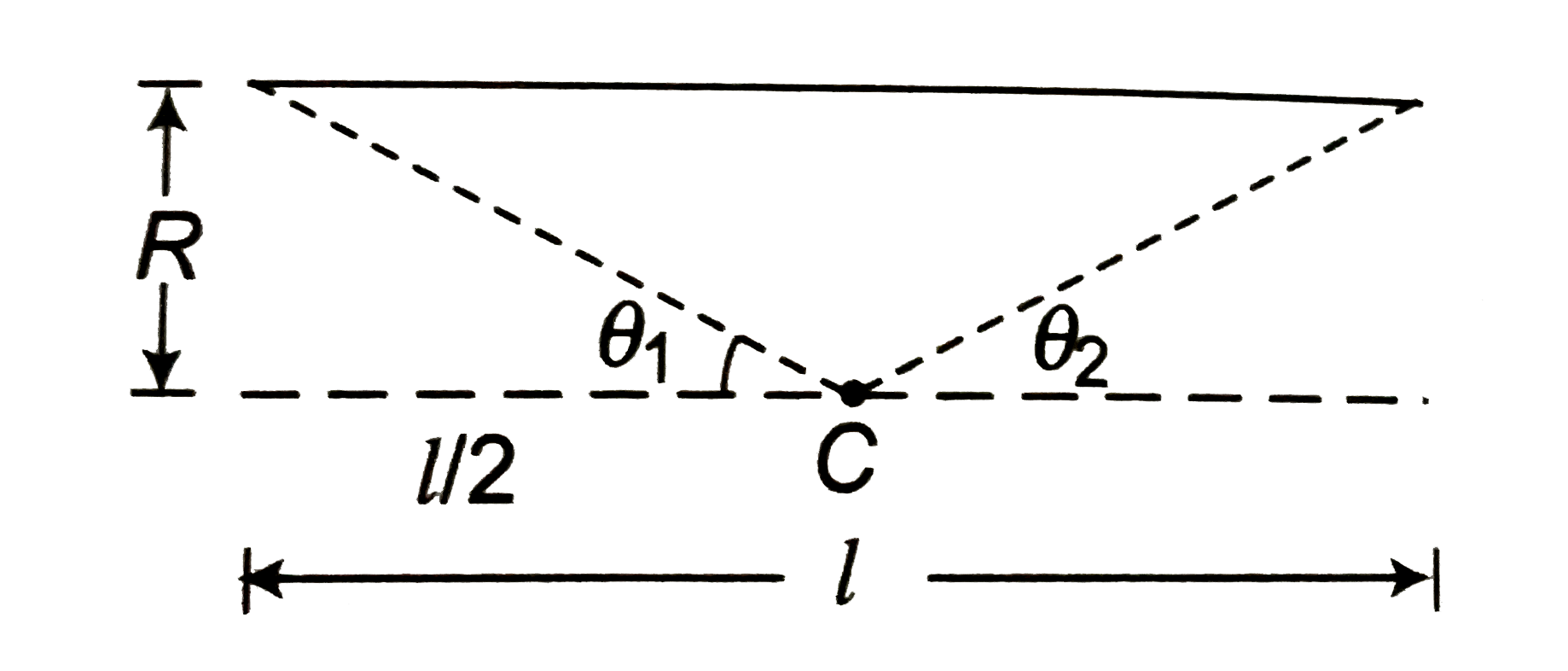 `cos theta_(1)=cos theta_(2)=(l//2)/(sqrt(R^(2)+(l//2)^(2)))=l/(sqrt(l^(2)+4R^(2)))` `B_(C)=1/2mu_(0)ni(cos theta_(1)+cos theta_(2))` `=1/2 mu_(0)nixx(2l)/(sqrt(l^(2)+4R^(2)))` `=(mu_(0)nil)/(sqrt(l^(2)+4R^(2)))=(mu_(0)ni)/(sqrt(l+(2R//l)^(2)))` If `l to oo, B_(C)=mu_(0)ni` (d) `i=5mA=5xx10^(-3) A, m=N//l=1000/0.4=2500` 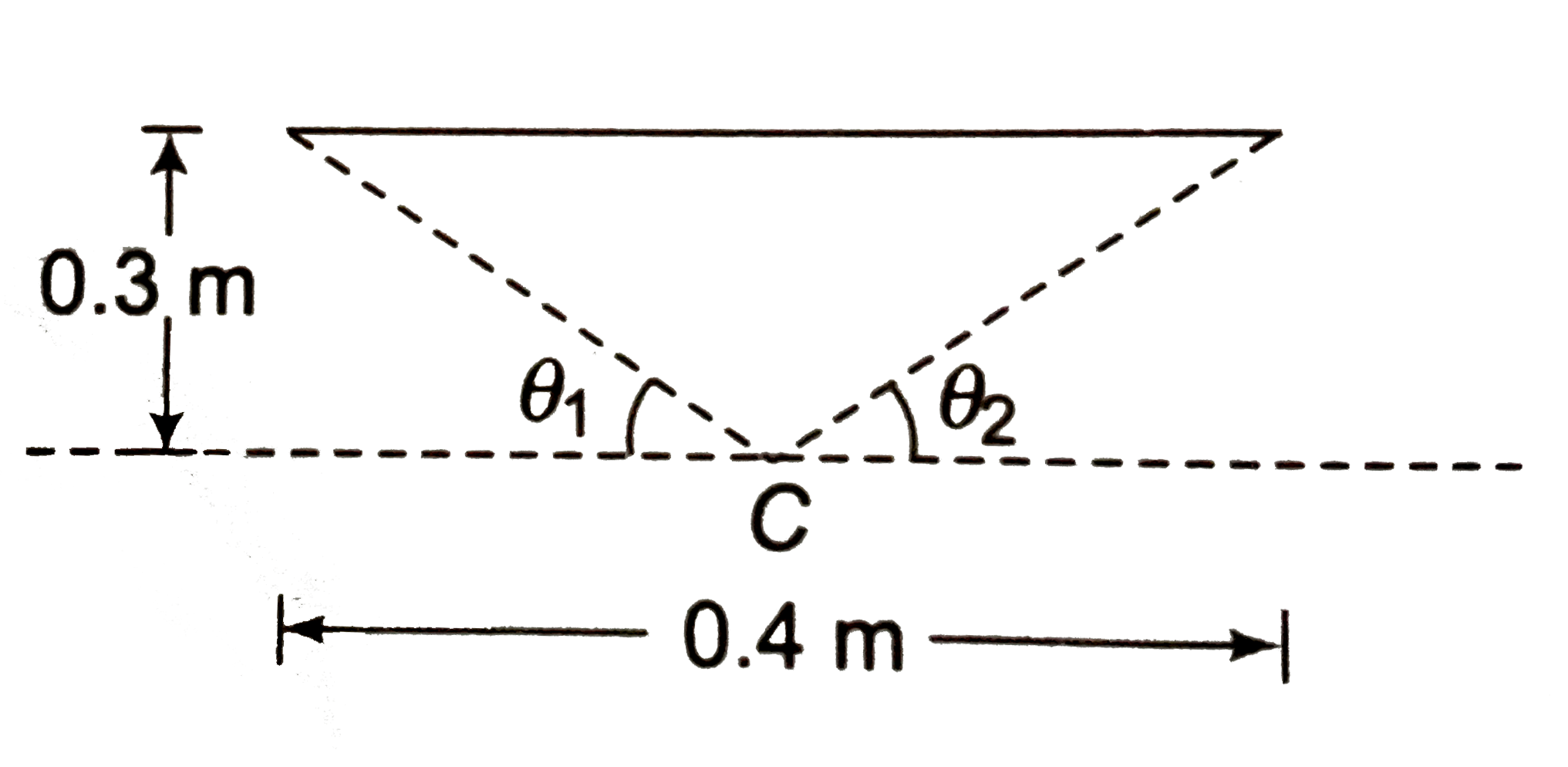 `cos theta_(1)=0.2/(sqrt((0.2)^(2)+(0.3)^(2)))=0.2/(sqrt(0.13))=2/(sqrt(13))` `B_(C)=1/2mu_(0)ni(cos theta_(1)+cos theta_(2))` `=1/2(4pixx10^(-7))(2500)(5xx10^(-3))xx2xx2/(sqrt(13))` `=(pixx10^(-5))/(sqrt(13)) T` At ENDS  `cos THETA=0.4/0.5=4/5=0.8` `B_(A)=1/2mu_(0)ni(cos 90^(@)+cos theta)` `=1/2(4pixx10^(-7))(2500)(5xx10^(-3))XX(0.8)` `=2pixx10^(-6) T` |
|
| 1780. |
List out the advantages of stationary armature-rotating field system of AC generator. |
|
Answer» Solution :i. The current is drawn directly from fixed terminals on the stator WITHOUT the use of brush contacts. ii. The INSULATION of stationary armature winding is easier. iii. The number of sliding contacts (slip rings) is reduced. MOREOVER, the sliding contacts are used for low-voltage DC Source. iv. Armature windings can be constructed more RIGIDLY to prevent deformation due to any mechanical STRESS. |
|
| 1781. |
कौन सा ग्राफ कण की विरामवस्था दर्शाता है - |
|
Answer» |
|
| 1782. |
Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field vecB such that |
|
Answer» B is perpendicular of v According to RIGHT hand screw rule direction of `ivec(dl)xxvecr` is perpendicular to magnetic FIELD. |
|
| 1783. |
How does Lencho feel when his crop is destroyed? |
|
Answer» Sad |
|
| 1785. |
In case (a) and (b) where will the magnetic field be maximum, measured on the perpendicular bisectro of the line of shortest distance between the two wires |
|
Answer» SOLUTION :(a) At a distance `(0.05 SQRT2)` m from each WIRE (B) At the mid-point of the line of shortest distance |
|
| 1786. |
State an expression for the moment of inertia of a solid uniform disc rotating about an axis passing through its centre, perpendicular to its plane. Hence derive an expression for the moment of inertia and radius of gyration. (i) about a tangent in the plane of the disc, and (ii) about a tangent perpendicular to the plane of the disc. In a set, 21 tuning forks are arranged in a series of decresing frequencies. Each tuning fork produces 4 beats per second with the preceding fork. If the first fork is an octave of the last fork , find the frequencies of the first and tenth forks. |
|
Answer» Solution :Moment of inertia for a solid uniform disc rotating about an axis passing through its centre, perpendicular to its plane, `I_(C )=(MR^(2))/(2)` `(i)` `M.I.` about DIAMETER `=(MR^(2))/(4)` `I_(t)=I_(d)+MR^(2)` [Using parallel axis theorem] `=(MR^(2))/(4)+MR^(2)=(5MR^(2))/(4)` RADIUS of gyration , `k=sqrt((I)/(M))=sqrt((5MR^(2))/(4M))` `k=(sqrt(5)R)/(2)` `(ii) I_(t)'=I_(c )+MR^(2)` [Using parallel axis theorem] `I_(t)'=(MR^(2))/(2)+MR^(2)=(3MR^(2))/(2)` `Mk'^(2)=(3MR^(2))/(2)` `k'=sqrt((3)/(2))*R` Numerical : Let, `n_(1)=`frequency of first tuning fork `n_(21)=`frequency of last tuning fork Difference in frequencies `(-d)` `=-4` beats/second `P=` number of tuning forks `n_(P)=n_(1)+(P-1)d` `n_(21)=n_(1)+(21-1)(-4)` `n_(21)=n_(1)-80`........`(i)` `n_(1)=2(n_(21))` (Given) `:.(n_(1))/(2)=n_(21)` `:. (n_(1))/(2)=n_(1)-80` [From equation `(i)`] `n_(1)=160Hz` `n_(10)=` frequency of `10th` tuning fork `n_(10)=n_(1)+(10-1)d` `n_(10)=160+9(-4)` `n_(10)=124Hz` |
|
| 1787. |
A galvanometer has current range 50mA and voltage range 0.5 volt.Resistance required in series with galvanometer to read voltage upto 5 volt is : |
|
Answer» `900Omega` |
|
| 1788. |
What is a satellite ? Obtain an expression for total energy of a satellite. |
| Answer» Solution :An artifical satellite is launched of with the help of multi STAGE rocketing. The rocket is first of all fired with velocity to reach the desired height. Now, the first stage is DETACHED itself and SECOND stage is fired to CHANGE the desired direction of satellite. Finally the last stage is fired to GIVE the desired velocity in horizontal direction. All there calculation are done in advance. | |
| 1789. |
A ring of area A and resistance R is placed on the axis of a solenoid. The mutual inductance between them is M. When the current in the solenoid changes at the rate of I, the magnetic moment of the ring is |
|
Answer» `ARMI` |
|
| 1790. |
An ideal heat engine working between 27^(@)C and 127^(@)C takes 400 cal of heat in one cycle. The work done is |
|
Answer» 75 cal `(1)/(4)=(dW)/(400)` `dW=100cal(eta=1-(300)/(400)=(1)/(4))` |
|
| 1791. |
Calculate and compare the energy realesed by (a) fusion of 1.0 kg of hydrogen deep within Sun and (b) the fission of 1.0 kg of ""^(235)U in a fission reactor. |
|
Answer» SOLUTION :1g of `""_(1)^(1)H` contain Avogadro.s number `:. 1kg ` of `""_(1)^(1)H` contains `6.023 xx 10^(23) xx 10^3` `4 ""_(1)^(1)H` is required for a reaction, hence `epsilon_1= (6.023 xx 10^23 xx 10^3 xx 26)/(4) = 39 xx 10^(26) MeV` For URANIUM, `epsilon_2 = (6.023 xx 10^(23) xx 10^3 xx 200)/(0.235) = 5.1 xx 10^(26) MeV` `epsilon_1` is NEARLY 8 times `epsilon_2`. |
|
| 1792. |
How will you convert a galvanometer into an ammeter? |
| Answer» SOLUTION :By connecting a LOW resistance CALLED .the shunt. parallel to the GALVANOMETER. | |
| 1793. |
A pulsed laser has an average output power of 4.0 W. Each pulse consists of light at wavelength 5.0xx10^(-7)m and has a 25 ms duration. How many photons are emitted in a single pulse? |
|
Answer» `1.0xx10^(17)` |
|
| 1794. |
Two identical thin circular, metal plates are at a small separation d. They are connected by a thin conducting rod (AB) of length d. Each plate has area A. An ideal spring of stiffness k is connected to a rigid support and midpoint of rod AB as shown in the figure. Spring is made of insulating material. The system is on a smooth horizontal surface. The entire region has a uniform vertical upward magnetic field B. The discs are pulled away from the support and released. Find time period of oscillations. Mass of the two disc plus rod system is M. Neglect any eddy current. |
|
Answer» |
|
| 1795. |
At room temperature (27^(@)C) the r.m.s speed of the molecules of a certain diatomic gas is found to be 1920 ms^(-1). The gas is: |
|
Answer» `O_(2)` `M=(3xx8 cdot 32xx300)/((1920)^(2))=2xx10^(-3) kg` `M=2g.` Thus, gas is HYDROGEN Hence, CORRECT CHOICE is (B). |
|
| 1796. |
Two wires of same material and length are stretchedby the same force. If the ratio of radii of the two wires in n:1 then the ratio of their elongation is |
|
Answer» `n^(2):1` `(l_(1))/(l_(2))=((r_(2))/(r_(1)))^(2)=(1)/(n^(2))` |
|
| 1797. |
Moseley.s law for characteristic X-rays is sqrtv=a(Z-b). In this |
|
Answer» Both .a. and .b. are INDEPENDENT of the MATERIAL |
|
| 1798. |
Which of the following word is used for a person who sees a crime occur? |
|
Answer» Criminal |
|
| 1799. |
Consider vec(F)=4hat(i) - 3hat(j). A vector perpendicular to vec(F) is : |
|
Answer» `6HAT(i)` |
|
| 1800. |
A Bi^(210) radionuclide decays via the chain Bi^(210)(beta^(-)-"decay")/(lambda_(1))Po^(210)(alpha-decay)/(lambda_(2)) Pb^(206) (stable), where the decay constants are lambda_(1) = 1.6 xx 10^(-6)s^(-1), T_(1//2) ~~ 5 days , lambda_(2) == 5.8 xx 10^(-8)s^(-1), T_(1//2) ~~ 4.6months. alpha & beta activites of the 1.00 mg a month after its manufacture is (x)/(5) xx 10^(11) Find x.2^((1)/(4.6)) = 0.86 |
|
Answer» LET `N_(A), N_(B)` and `N_(C )` be the no of nuclei of `Bi^(210), Po^(210)` and `Pb^(208)` respectively. `N_(0)` be the no of nuclei of `Bi^(210)` at `t=0` `N_(0)=(1xx10^(-3))/(210)xx6.02xx10^(23) ""~~2.9xx10^(18)` `(dN_(A))/(dt)= -lambda_(1)N_(A)"_____"`I `(dN_(B))/(dt)=-lambda_(2)N_(B)+lambda_(1)N_(A)"______"`(II) `(dN_(c ))/(dt)= lambda_(2)N_(B)"_____"`III Solving equ. I , we get `N_(A)= "No" e^(-)lambda_(1)t` From EQUATION II, `(dN_(B))/(dt)=-lambda_(2)N_(B)+lambda_(1)N_(o)e^(-lambda_(1)t)` This is first order line differential equation. On solving we get `N_(B)=e^(-lambda_(2)t)[(lambda_(1)N_(0))/(lambda_(2)-lambda_(1))e^((lambda_(2)-lambda_(2))t)+C]` where `C` is a constant The value of `C` can be OBTAINED by taking `t-0, N_(B)=0` `rArrC=(lambda_(1)N_(0))/(lambda_(1)-lambda_(2))` `:. N_(B)=(lambda_(1)N_(o))/(lambda_(1)-lambda_(2))[e^(-lambda_(2)t)-e^(-lambda_(1)t)] :. beta`-activity `A_(B)=|(dN_(A))/(dt)|=N_(0)lambda_(1)e^(-lambda_(1)t)=2.9xx10^(18)xx1.6xx10^(-6)xx(1)/(2^(6))S^(-1)=0.72xx10^(11)S^(-1)` `ALPHA`-activity `A_(alpha)=lambda_(2)N_(B)=(lambda_(1)lambda_(2)N_(0))/(lambda_(1)-lambda_(2))(e^(-lambda_(2)t)-e^(-lambda_(1)t))~~(lambda_(1)lambda_(2)N_(0))/(lambda_(1))e^(-lambda_(2)t)=(lambda_(2)N_(0))/((1)/(2^(4xx6)))=1.4xx10^(11)s^(-1)` |
|