Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2301. |
10^6 electrons are moving through a wire per second, the current developed is: |
|
Answer» `1.6xx10^(-19)` |
|
| 2302. |
Determine the current drawn from a 12 V supply with internal resistance 0.5Omegaby the infinite network shown in Fig. Each resistor has 1Omega resistance. |
Answer» Solution :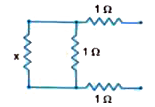 The infinite network consists of NUMBER of RESISTANCE elementary units. Let x be the EQUIVALENTRESISTANCE of the infinite ladder. Then adding one more elementary resistance unit with the infinite ladder will not affect the total resistance of the infinite ladder. The combination, therefore, can be made equivalent to as shown in Fig. Here, x is the equivalent resistance of the given infinite network. Thus, the total resistance ` x = (1)/(1/x + 1/1) + 1 +1 = (x)/(x + 1) +2 = (2 + 3X)/(1 + x)` `rArr x + x^2 = 2 + 3x` ` rArr x^2 - 2x - 2 = 0` which gives` x = (2 pm sqrt(4 + 8) )/(2) = 1 pm sqrt3` As `x = 1 - sqrt3` is not possible, hence `x = 1+ sqrt3 = 1+1.732 = 2.732 OMEGA` The current drawn from the 12 V supply having internal resistance of 0.5 `Omega`, `I = (12)/(2.732 + 0.5) = (12)/(3.232) = 3.71 A` |
|
| 2303. |
A source of frequency 10 kHz when vibrated over the mouth of a closed organ pipe is in unison at 300K. Find the beats produced when temperature rises by 1K |
| Answer» SOLUTION :16.67 HZ | |
| 2304. |
The diagram shows a logic network. Which single gate is equivalent to the network? |
|
Answer» `EX-NOR` GATE The NETWORK can be REPRESENTED by a SINGLE `EX-OR`gate. |
|
| 2305. |
Obtain the expression for fringe width of interference fringes in Young's double slit experiment. |
Answer» Solution :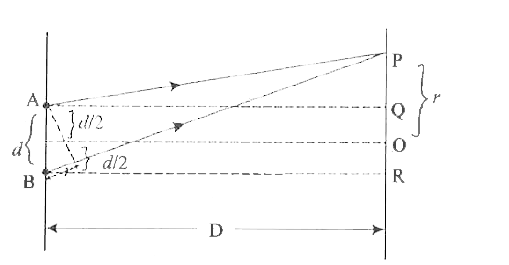 A and B REPRESENTED two coherent SOURCES separated by a distance d. Let a screen be PLACED at a distanceD from the sources. The point `THETA` on the screen is equidistant from A and B . It is given BP-AP=`delta` eqn.(1)-(2) Then `delta=BP^2-AP^2` In the `triangle^"le"` BRP, `BP^2=BR^2+PR^2=D^2+(PO+OR)^2` `BP^2=D^2+(x + d//2)^2`...(1) In the `triangle^"le"` APQ, `AP^2 =AQ^2 +QP^2 =D^2 + (OP-OQ)^2` `AP^2 =D^2 +(x - d//2)^2` ....(2) `BP^2-AP^2=D^2+(x+d//2)^2 -D^2 +(x-d//2)^2` `=[D^2+x^2+d^2/4+2xd//2] -[D^2+x^2+d^2/4-2xd//2]` `=cancelD^2+cancelx^2+cancel(d^2/4)+XD -cancelD^2-x^2-cancel(d^2/4)+xd` =xd+xd=2xd `(BP^2-AP^2)=2xd` (BP-AP)(BP+AP)=2xd `BP-AP=(2xd)/((BP+AP))` BP-AP=`(cancel2xd)/(cancel2D)` P is very close to D Path Difference `Delta=(xd)/D "" Delta` is not shown in drawing . For constructive interference `delta=nlambda` `nlambda=(xd)/D rArr x=(Dnlambda)/d` `x_1=(Dlambda)/drArr x_2=(2Dlambda)/d` The distance between the centers of any two consecutive bright fringes is called the fringe width. `beta=x_2-x_1=(2Dlambda)/d-(Dlambda)/d` `beta=(Dlambda)/d` |
|
| 2306. |
In a plane electromagnetic wave of frequency 1.0xx10^(12) Hz, the amplitude of the magnetic field is 5.0xx10^(-6)T.a.Calculate the amplitude of the electric field.b.What is the total average energy density ? |
|
Answer» Solution :a. `1.5xx10^(3)VM^(-1)` b.`10^(-5)JM^(-3)` |
|
| 2307. |
An electric potential difference will be induced between the ends of the conductor shown in the figure, if the conductor moves in the direction shown by |
|
Answer» P |
|
| 2308. |
The de Brogle wavelength of an electron accelrated to a potential of 400 V is approximately |
|
Answer» 0.03 nm `lambda=(6.625xx10^(-34))/(sqrt(2xx9.1xx10^(-31)xx1.6xx10^(-19)xx400))` `lambda=(6.625xx10^(-34))/(sqrt(11648xx10^(-50)))` `lambda=(6.625xx10^(-34))/(107.925xx10^(-25))` `lambda=0.06138xx10^(-34+25)` `lambda=0.06138xx10^(-9)` `lambda=0.06nm` |
|
| 2309. |
A potentiometer wire has length 4 m and resistance 8Omega. The resistance that must be connected in series with the wire and an accumulator of e.m.f. 2V, so as to get a potential gradient 1 mV per cm on the wire is: |
|
Answer» `44Omega` |
|
| 2310. |
Describe briefly, with the help of a labelled diagram, the basic elements of an a.c generator. State its underlying principle. Show diagrammatically how an alternating emf is generated by a loop of wire rotating in a magnetic field. Write the expression for the instantaneous value of the emf induced in the rotating loop. |
|
Answer» Solution :For labelled diagram of an AC generator, see Fig. 6.55. Construction : An a.c. generator consists of the following four PARTS : (i) Armature: It is a RECTANGULAR coil consisting of a large number of turns of insulated copper wire wound over a laminated soft iron core. The coil can be rotated about its central axis. (ii) Field magnet: Nand S are the pole pieces of a strong electromagnet, between which the armature coil is rotated. (iii) Slip rings : `R_(1) and R_(2)` are two hollow metallic rings, to which two ends of armature coil are connected. The rings rotate with the rotation of the coil. (iv) Brushes : `B_(1) and B_(2)` are two flexible metal plates, which are fixed and are kept in light contact with slip rings. PRINCIPLE : See Short Answer Question Number 53. Theory and Working: As the armature coil ABCD is rotated in the magnetic field, angle between the field and normal to the coil changes continuously. Therefore, the magnetic flux linked with the coil changes and an emf is induced in the coil. Let initially, the armature coil be moving as shown in Fig. 6.59(a) so that AB moves outwards (towards us) and CD inwards (into the paper). The amount of magnetic flux linked with the coil is changing and in accordance with Fleming.s right hand rule, induced current in AB is from A to B and in CD it is from C to D. In the external circuit current flows from `B_(2) to B_(1)`. After half the rotation of the coil, AB moves inwards and CD outwards as shown in Fig. 6.59 (b). Now applying Fleming.s right hand rule, we find that the induced current in AB is from B to A and in CD  it is from D to C. In the external circuit, current flows from B to B . Thus, it is clear that the induced current in the external circuit changes its direction after every half rotation of the coil. Hence, the current induced is alternating in nature. it is from D to C. In the external circuit, current flows from B to B . Thus, it is clear that the induced current in the external circuit changes its direction after every half rotation of the coil. Hence, the current induced is alternating in nature. Whenever plane of armature coil is perpendicular to the magnetic field, magnetic flux linked with the coil is maximum but change in magnetic flux is ZERO and hence magnitude of induced emf/current is zero. However, when plane of armature coil is parallel to the magnetic field, magnetic flux linked with the coil is zero and change in magnetic flux is maximum. Hence the magnitude of induced emf is maximum. In this manner, magnitude of induced emf/current goes on changing continuously For expression of induced emf, see Short Answer Question Number 53. |
|
| 2311. |
In Fig. 27-39, a voltmeter of resistance R_v= 300 Omega and ammeter of resistance R_A= 3.00 Omega are being used to measure a resistance R in a circuit that also contains a resistance R_(0) =100 Omega and an ideal battery with an emf of epsi = 18.0 V. Resistance R is given by R =V/i, where V is the potential across R and i is the ammeter reading. The voltmeter reading is V', which is V plus the potential dilference across the ammeter. Thus, the ratio of the two meter readings is not R but only an apparent resistance R' -V/i. If R =85.0Omega what are (a) the ammeter reading. (b) the voltmeter reading, and (c) R'? (a) If R_A is decreased, does the difference between R' and R increase, decrease, or remain the same? |
|
Answer» |
|
| 2312. |
Which are the two properties required for a material to be used as a core of electromagnets. |
| Answer» Solution :Magnetic material should have 1. High permeability 2. Low RETENTIVITY 3. Low hystersis LOSS | |
| 2313. |
(a) In a frame of reference S_(1), though the net force is zero, the net acceleration is not zero.(b) In a frame of reference S_(2), though the net force is not zero, the net acceleration is zero.(c ) In a frame of reference S_(3), the net acceleration is zero whenever the net force is zero. |
|
Answer» `S_(1)` and `S_(3)` are inertial and `S_(2)` is NON - inertial |
|
| 2314. |
The magnitude of the magnetic field inside a long solenoid is increased by |
|
Answer» a. DECREASING its radius |
|
| 2315. |
The audio signal |
|
Answer» can be sent DIRECTLY over the AIR for large DISTANCE |
|
| 2316. |
Consider curve y=(1+x)^(y)+sin^(-1)(sin^(2)x). Which of the following statements are correct ? |
|
Answer» A NORMAL to the at x=0 makes equal intercept with axes |
|
| 2317. |
Column A gives a list of possible set of parameters measured in some experiments . The variations of the parameters in the form of graphs are shown in column B. |
|
Answer» |
|
| 2318. |
What it contains. |
| Answer» Solution :it is PHENOMENON which keeps the EARTH.s surface warm at night.The earth REFLECTS back infrared part of SOLAR radiation. | |
| 2319. |
As the value of impact parameter is larger the scattering angle is ...... |
|
Answer» constant |
|
| 2320. |
Transmission lines transmit a voltage V volt to our houses from stations, then the power P supplied by them is proportional to: |
|
Answer» 1/V |
|
| 2321. |
Statement A : A proton has spin and magnetic moment just like an electron. But its effect is neglected in magnetism of material. Statement B : The order of magnitude of difference between the diamagnetic suceptibility of N_(2)(~5xx10^(-9))("STP")andCu(~10^(-5))" is "1.6xx10^(-4) Statement C : Suppose we went to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole P in an electrostatic field E and (ii) magnetic dipole M in a magnetic field B. Set of conditions on E,B,p,M so that the two motions are verified to be identical. (Assume identical initial contiditions are (i) P=M/C (ii) PE = MB |
|
Answer» A correct B correct C correct `M=(eh)/(4pim)orMprop1/m` `(because(eh)/(4pi)="constant")` `thereforeM_(p)/M_(e)=m_(e)/m_(p)=M_(e)/(1837M_(e))` `(becauseM_(p)=1837M_(e))` `rArrM_(p)/M_(e)=1/1837ltlt1` `rArrM_(p)ltltM_(e)` Thus, EFFECT of magnetic moment of proton is neglected as compared to that of electron. B) We know that Density of nitrogen `rho_(N_(2))=(28g)/(22.4L)=(28g)/(22400c c)` Also, density of copper `rho_(Cu)=(8g)/(22.4L)=(8g)/(22400c c)` Now, comparing both densities `rho_(N_(2))/rho_(Cu)=(28)/(22400)xx(1)/(8)=1.6xx10^(-4)` Also given `x_(N_(2))/X_(cu)=(5XX10^(-9))/(10^(-5))=5xx10^(-4)` We know that, `x=("Magnetisation(M)")/("Magnetic int ensity(H)")` = `M/(HV)=M/(H("mass"//"density"))=M_(p)/(Hm)` `thereforexproprho" ""Hence"," "x_(N_(2))/x_(Cu)=rho_(N_(2))/rho_(Cu)=1.6xx10^(-4)` Thus, the order of magnitude difference or major difference between the diamagnetic susceptibility of `N_(2)` and Cu is accounted for by the ratio of densities. C) Now, SUPPOSE that the angle between M and B is `theta` Torque on magnetic dipole moment M in magnetic field B. `tau.=MBsintheta` Two motions will be identical, if `pEsintheta=MBsintheta` `rArrpE=MB` But, `E=cB` `therefore` Putting this value in Eq. (i), `pcB=MB` `rArrp=M/c` |
|
| 2322. |
a concave mirror of focal length f produces an image n times, the size of the object. If the image is real, then the distance of the object from the mirror is : |
|
Answer» (N - 1)F |
|
| 2323. |
An explorer is caught in a whiteout (in which the snowfall is so thick that the ground cannot be distinguished from the sky) while returning to base camp. He was supposed to trave due north for 4.8km, but when the snow clears, he discovers that he actually traveled 7.8 km at 50^(@) north of due east. (a) How far and (b) in what direction must he now travel to reach base camp ? |
| Answer» Solution :`(a) 5.1 KM, (b) 13.3^(@),` SOUTH of due WEST | |
| 2324. |
A neutral point is found on the prolongation of the axis of a bar magnet at a distance of 0.1 m from the nearest pole. If the length of the bar be 0.1m and the B-field of earth = 0.36 xx 10^(-4) tesla, find the pole strength of the magnet. |
|
Answer» |
|
| 2325. |
In the series LCR circuit , the power dissipation is through |
| Answer» Solution :R | |
| 2326. |
By sandwitching a thin layer of n-type semiconductor between two-p-type semiconductors we get. |
|
Answer» |
|
| 2327. |
The manganin wire is used in the preparation of standard resistance. Why? |
| Answer» SOLUTION :For MANGANIN temperature coefficient of resistance `(ALPHA)` is very very SMALL. So change in resistance of the manganin wire with temperature is almost negligible. So it is used to prepare standard resistance. | |
| 2328. |
A 4cm object is placed perpendicular to the principal axis of a convex mirror of focal length 7.5cm.The distance of the image from the mirror if it is 0.6 cm in size is 51/x where x is |
|
Answer» |
|
| 2329. |
A charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube |
|
Answer» `Q//epsilon_0` |
|
| 2330. |
The force between two similar charges of magnitude 2C each separated by a distance 2km |
| Answer» Answer :B | |
| 2331. |
Two beams, A and B, of plane polarised light with mutually perpendicular planes of polarisation are seen through a polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam A has maximum intensity (and beam B has zero intensity). a rotation of Polaroid through 30^@ makes the two beams appear equally bright. If the intiial intensities of the two beams are I_A and I_B respectively, then I_A//I_B equals : |
Answer» Solution :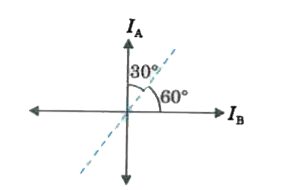 `I_A = cos^2 30^@ = I_B cos^2 60^@` `I_A((sqrt(3))/(2))^(2) = I_B (1/2)^2` `I_A (3/4) = I_B (1/4)` `(I_A)/(I_B) = 1/3` |
|
| 2332. |
If vecA= 3 hati+4hatj and vecB=7hati+24 hatj, ind a vector having the same magnitude as B and parallel to vecA |
|
Answer» Solution :The VECTOR parallel to `vecA` and having magnitude of `vecB` is `vecC=|vecB|(vecA)/(|vecA|)=|vecB|hatA "" B= sqrt(7^(2)+24^(2))=25` and `hatA=(vecA)/(A)=(3hati+4hatj)/(sqrt(3^(2)+4^(2)))=(1)/(5) (3hati+4hatj)` `vecC=25xx(1)/(5)(3hati+4hatj=15 hati+20 HATJ)` |
|
| 2333. |
A dielectric disc of radius R and uniform positive surface charge density sigma is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is (q)/(m)=(4epsion_(0)g)/(sigma). (i). Find the value of H if the particle just reaches the disc. (ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position. |
|
Answer» (II). `H=(R)/(SQRT(3))` |
|
| 2335. |
What is the peak value of induced e.m.f. in a rotating coil? |
|
Answer» Solution :`E_0` = NAB_0, `E_0` = PEAK value N = NO. of TURNS A = Area of coil B = Magnetic induction. Angular VELOCITY. |
|
| 2336. |
In a YDSE experiment, the distance between the slits & the screen is 100 cm. For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25 mm. When the distance between the slits is increased by Deltad=1.2 mm, the fringe width decreased to n=2//3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light. |
|
Answer» `rArr 0.25xx10^(-3)=(lambda)/(d)xx1 m` `rArr (lambda)/(d)=2.5xx10^(-4)…………..(1)` Afterwards : `(2)/(3) beta_(i) =(lambdaD)/((d+Deltad))` `rArr (lambda)/(d+Deltad)=(2)/(3)xx(2.5xx10^(-4))/(1)..............(2)` Dividing `(1) and (2)` `(d+Deltad)/(d)=(3)/(2) rArr d=2 (Deltad) =2.4 mm`. `& lambda=2.4xx2.5xx10^(-7)m = 600 nm`. Now `P` becomes central maxima. `rArr` for point `P : d sintheta =(mu-1)t` `rArr d. TANTHETA approx (mu-1)t` `rArr d(20beta)/(D) =(mu-1)t` `rArr (d)/(D)xx(20xxlambdaD)/(d) =(1.5-1)t` `rArr t=(20lambda)/(0.5) =(20xx600xx10^(-9))/(0.5)=24 MUM`. 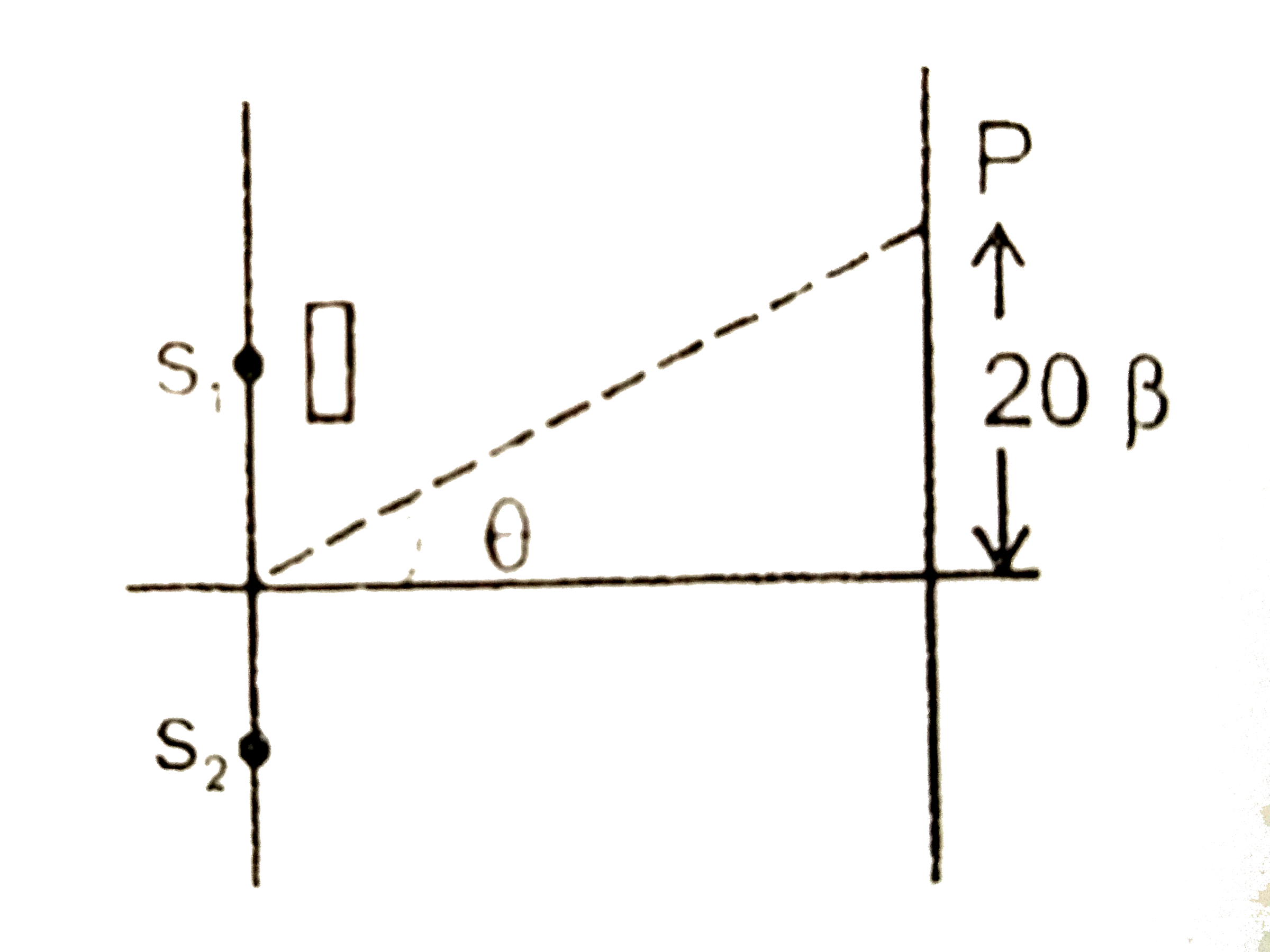
|
|
| 2337. |
If the height of TV tower is increased by 21%, then the transmission range is enhanced by |
| Answer» ANSWER :A | |
| 2338. |
When sunlight falls normally on earth, a luminous flux of 1.57 xx 10^(5) "lumen"//m^(2) is produced on earth. The distance of earth from sun is 1.5 xx 10^(8) Km. The luminous intensity of sun in candela will be |
|
Answer» `3.53 XX 10^(27)` |
|
| 2339. |
The radiiof curvature of two surfacesof a convex lensis 0.2 m and 0.22 m. Find thefocal length of the lensif refractiveindexof the materialof lens is 1.5 . Also find thechange in focal length, if it is immersedin water of refractiveindex1.33. |
|
Answer» SOLUTION :Given :`R_1+0.2m`, `R_2=-0.22`m , `n=1.5 , n_W=1.33` W.k.t.`1/t=(n_2-1)(1/R_1-1/R_2)` i.e., `1/f =(1.5-1)(1/0.2+1/0.22)` i.e.,`1/f=0.5xx(5+4.55)`=4.78 Hence `f=1/4.78`=0.209 m but `f_(w)/(f_a)=(n_r-1)/(._ln_g-1)` i.e, `f_(w)/(f_a)=(1.5-1)/(1.5/1.33-1)=3.91` i.e., `f_w`=3.91`f_n` `=3.91xx0.209` =0.817 m Focal lengthof lens in water = 0.817 m |
|
| 2340. |
In the below figure, an electron of mass m, charge-e, and low(negligible) speed enters the region between two plates of potential difference V and plate separation d, initially headed directly toward the top plate. A uniform magnetic field of magnitude B is normal to the plane of the figure. Find the minimum value of B such that the electron will not strike the top plate. |
|
Answer» `sqrt((2mV)/(ed^(2))` |
|
| 2341. |
What is the difference between a galvanometer and an ammeter? |
| Answer» SOLUTION :The presence of current is detected USING GALVANOMETER. The intensity or strength of current is MEASURED using an AMMETER. | |
| 2342. |
Unpolarised light of intensity I_(0) falls on a Nicol prism. The light emerging from this Nicol Prism falls on another Nicol whose polarising axis is inclined to that of first by an angle 30^(@). The light emerging from the second Nicol has the intensity : |
|
Answer» `(I_(0))/(SQRT(2))` |
|
| 2343. |
(A ): The surface densities of two spherical conductors of different radii are equal. Then the electric field intensities near their surface are also equal. (R ): Surface density is equal to charge per unit area. |
|
Answer» Both .A. and .R. are true and .R. is the correct EXPLANATION of .A. |
|
| 2344. |
The variation of pressure P with volume V for an ideal monatomic gas during an adiabatic process is hown in figure. At the magnitude of rate of change of pressure with volume is- |
|
Answer» `(3P_(0))/(5V_(0))` |
|
| 2345. |
Power delivered by the source of an a.c. circuit is maximum when |
|
Answer» `L omega =Comega` |
|
| 2346. |
For any charge configuration equipotential surface through a point is normal to the electric field. Justify. |
| Answer» Solution :No work is being DONE in moving a charge along an equipotential surface. HENCE, COMPONENT of ELECTRIC field along the equipotential surface is zero and electric field is perpendicular to the equipotential surface. | |
| 2347. |
What is her occupation? |
|
Answer» Environmentalist |
|
| 2348. |
In the circuit shown below, all the three voltmeters are identical and have very high resistance. Each resistor has the same resistance The voltage of the ideal battery shown is 9 V Find the reading of voltmeter V_(3) (in volts) |
Answer»  LET `V_(D)` be potential of point D then sum of charged reaching point D is zero `(V_(B)-V_(D))/R_(v_2)+(V_(B')-V_(D))/R_(v_(1))+((V_(C)-V_(D)))/R_(v_(3))=0[R_(v_(1))-R_(v_(1))=R_(v_(3))=R]` Rightarrow`(3-V_(D))/R+(3-V_(D))/R+(6-V_(D))/R=0` `Rightarrow 12-3V_(D)=0,V_(D)=4` volts reading of `V_(3)=2` volts |
|
| 2349. |
The order of magnitude of the density of nuclear matter is .................. |
| Answer» SOLUTION :`10^(17)KGM^(-3)` | |
| 2350. |
(A) : If a body moving in a circular path with constant speed, then no force acts on it. (R ) : The direction of the velocity vector of a body moving in a circular path is changing |
|
Answer» Both (A) and (R) are TRUE and (R) is the correct EXPLANATION of (A) |
|