Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2351. |
Four equal charges Q are placed at the four corners of a square of each side is .a. . Work done in moving a charge -Q from its centre to infinit |
|
Answer» ZERO |
|
| 2352. |
A conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then |
|
Answer» the rod MOVES with constant velocity `:. F-CB^(2)l^(2)a=ma` `rArr a=(F)/(M+B^(2)l^(2)C)` `rArr`emf increases `rArr ` charge INCREASE. |
|
| 2353. |
The r.m.s. speed of oxygen is v at a particular temperature. If the temperature is doubled and oxygen molecule dissociate into oxygen atoms, the r.m.s. speed becomes |
|
Answer» v For OXYGEN molecules at temperature T, `v_(rms)=v=sqrt((3RT)/(M))""...(i)` Now, temperature is doubled and oxygen molecules dissociate into oxygen atom (molar mass BECOMES `M//2`) then rms speed will be `v._(rms)=sqrt((3R(2T))/((M//2)))=2sqrt((3RT)/(M))=2v` [USING eqn(i)] |
|
| 2354. |
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60^@ , and one of the fields has a magnitude of 1.2 xx 10^(-2) T. If the dipole comes to stable equilibrium at an angle of 15^@ with this field, what is the magnitude of the other field ? |
| Answer» SOLUTION :`4.4 XX 10^(-3) T ` | |
| 2355. |
Which one of the following is a non-magnetic substance |
|
Answer» Iron |
|
| 2356. |
In an metre bridge, the null point is found at a distance of 33.7 cm from A. If now a resistance of 2Omega is connected in parallel with S, the null point occurs at 51.9 cm. Determine the value of R and S. |
|
Answer» Solution :From the first balance point, `(R )/(S)=(33.7)/(66.3)"….(i)"` After S is connected in PARALLEL with a resistance of `12Omega`, the resistance across the gap changes from S to `S_(eq)`, where `S_(eq)=(12S)/(S+12)` and hence the new balance CONDITION gives `(51.9)/(48.1)=(R )/(S_("eq))=(R(S+12))/(12S)` SUBSTITUTING the value of R/S from equation (i), we get `(51.9)/(48.1)=(S+12)/(12).(33.7)/(66.3)`, which gives `S=13.5Oemga` Using the value of `R//S` above, we get `R=6.86Omega`. |
|
| 2357. |
In Problem 29, what ratio m/M gives the least gravitational potential energy for the system? |
| Answer» SOLUTION :`m//M = 1//2` | |
| 2359. |
The graph between angle of deviation (delta) and angle of incidence (i) for a triangular prism is represented by |
|
Answer» ` |
|
| 2360. |
The two plates X and Y of a parallel-plate capacitor of capacitacne C are given a charge of amount Q each. X is now joined to the positive terminal and Y to the negative terminal of a cell of emf varepsilon=Q//C. |
|
Answer» Charge of amount `Q` will flow fromte positive terminal to the NEGATIVE terminal of the CELL through the capacitor. |
|
| 2361. |
Two point charges q and - are separated by a distance 2L. Find the flux of the electric field vector across the circle of radius R is shown. |
|
Answer» `(q)/( 2 in _0){1- (d)/(sqrt(d^2+r^2))}` |
|
| 2362. |
When stopping potential is applied in an experiment on photoelectric effect, nophotocurrent is observed. This means that. |
|
Answer» The EMISSION of photoelectrons is STOPPED |
|
| 2363. |
Of the three types of mirros: plane, concave, and convex, (a) which will have larger field of view, if aperture of all the three mirrors is the same? (b) Can you think of a practical application of this? |
| Answer» SOLUTION :(a) Convex MIRRORS (b) THEREFORE they are used in REAR VIEW mirrors | |
| 2364. |
In a given optical bench, a needle of length 10 cm is used to estimate bench error. Thhe object needle, image needle & lens holder have their reading as shown. X_(0)=1.1 X_(I)=21.0cm X_(L)=10.9cm Extimate the bench errors which are present in image needle holder and object needle holder. Also find the focal length of the convex lens when. X_(0)=0.6cm X_(I)=22.5cm X_(L)=11.4cm |
|
Answer» |
|
| 2366. |
is temperature of surroundings in K, then the value of K on the basis of Stefan-Boltzmann law is 4^@C//mt and when the temperature becomes 50^@C the rate of cooling becomes 2^@C//mt. The temperature of surroundings is – |
| Answer» ANSWER :D | |
| 2367. |
Can one consider the temperature 20 and 30K as low for to 0.226 and 0.760J//(mol.K)? |
|
Answer» Solution :At LOW temperature `C prop T^(3)`. This is also a test of the "lowness" of the temperature We see that `((C_(1))/(C_(2)))^(1//3)=1.4982~~ 1.5=(T_(1))/(T_(2))=(30)/(20)` THUS `T^(3)` law is OBEYED and `T_(1),T_(2)` can we REGARDED low. |
|
| 2368. |
The half life of ._38^90Sr is 28 years. The disintegration rate of 15 mg of this isotope is of the order of |
|
Answer» `10^11` Bq Asnumber of ATOMS in 90 G of `._38^90Sr=6.023xx10^23` `therefore ` NUMBER of atoms in 15 mg of `._38^90Sr =(6.023xx10^23)/90xx15/1000` i.e., `N=1.0038xx10^20` Rate of DISINTEGRATION, `=0.693/T N=(0.693xx1.0038xx10^20)/(28xx3.15xx10^7)` `=7.877xx10^10 "Bq" approx 10^10` Bq |
|
| 2369. |
A charged particle moves at right angles to a uniform magnetic field and rotates in a circular path. The frequency of the charge does not depend on |
|
Answer» speed |
|
| 2370. |
Electrical field intensity is given as barE=(2x+1)yhati+x(x+1)hatj. The potential of a point (1,2) if potential at origin is 2 volt ils |
|
Answer» 2V |
|
| 2371. |
Welders wear special glass goggles ro facemask with glass window to protect their eyes from |
| Answer» Solution : This is because the special glass GOGGLES PROTECT the EYES from LARGE amount of UV radiations produced by WELDING arcs. | |
| 2372. |
A biconvex lens has a focal length 2/3 times the radius of curvature of either surface. Calculate the refractive index of lens material. |
|
Answer» Solution :It is given that for a BICONVEX lens `|R_(1)| = |R_(2)| = R` (SAY) and focal length of lens `|f| =2/3 R` APPLYING lens maker.s formula `1/f = (n-1) (1/R_(1) -1/R_(2))`, we get `1/(+2/3R) = (n-1) [1/(+R) -1/(-R)]` or `3/(2R) = (n-1) 2/R rArr n= 7/4 = 1.75` |
|
| 2373. |
Fig shows electric lines of force emerging from a charged body. Is electric field intensity more at A or B? |
| Answer» Solution :An ELECTRIC field is represented by electric lines of FORCE. If they are CLOSELY spaced, the electric field INTENSITY is more at that place. since field lines are closely spaced at A and widely spaced at`E_(B) gt E_(A)`. | |
| 2374. |
If the forward voltage in a semiconductor is doubled, the width of depletion layer will |
| Answer» Answer :A | |
| 2375. |
The electromagnetic wave having the shortest wavelength is |
|
Answer» a. X-RAYS |
|
| 2376. |
In Young.s double slit experiment ,the two slits act as sources of equal amplitude A and wavelengthlambda. In another experiment with the same setup the two slitsare sources of equal amplitude A and wavelength lambdabut are incoherent . The ratio of the intensityof lightat themidpointof the screen in the first case to that in the secondcase is |
|
Answer» `1:1` |
|
| 2377. |
If P represents radiation pressure, C speed of light, and Q radiation energy striking unit area per second and x,y,z are non zero integers, then P Q' C is dimensionless. The values of X,y and z are respectively |
|
Answer» 1,1,-1 |
|
| 2378. |
Give the explanation of reason behind the origin of motional induced emf. |
Answer» Solution :When a conducting rod is moving in to a magnetic field as shown in figure the positive ions and electrons MOVE along with it. 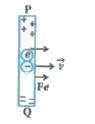 In the figure such particles will be in motion with velocity `vecv` PERPENDICULAR to the magnetic - field `vecB` and hence they experience a Lorentz force `vecF = Q(vecvxxvecB)` . Here positive ions will experience force from Q to P but as they remain fixed at their lattice positions no motion is produced. Now the force acting on electrons will be from P to Q. since electrons are free to move they accumulate at end Q. Due to this positive CHARGE opens up at end Q i.e. end P BECOMES positive and end Q becomes negative and hence the rod behaves as a battery of emf Bvl. |
|
| 2379. |
In Bohr model of hydrogen atom, let R,v and E represent the radius of robit, speed of the electron and total energyy of electron respectively. Which of following quantities are directly proportional to quantum number n? |
|
Answer» `VR` `impliesvRpropn` and `v/Epropn` |
|
| 2380. |
ABC is an equilateral triangle of side 2m. If vec(E ) = 10 NC^(-1) then V_(A) - V_(B) is |
| Answer» Answer :B | |
| 2381. |
There vectors veca, vecb and vecc each have a magnitude of 50m and lie in an xy plane. Their directions relative to the positive direction of the x axis are 30^(@), 195 ^(@), and 315^(@), respectively. What are (a) the magnitude and (b) the angleof the vector veca + vecb + vecc, and (c ) the magnitude and (d) the angle of veca - vecb - vecc ? What are the (e) magnitude and (f) angle of a fourth vector vecd such that (veca + vecb) - (vecc+ vecd)=0 ? |
| Answer» Solution :`(a) 38M, (b) - 375^(@), (C ) 130 m, (d) 12 ^(@) (E) 62 m, (f) 130^(@)` | |
| 2382. |
In Young's double slit experiment, the two slits act as coherent sources of waves of equal amplitude A and wavelength lambda. In another experiment with the same arrangement the two slits are made to act as incoherent sources of wave of same amplitude and wavelength. If the intensity at the middle point of the screen in the first case is l, and in the second case is I_(2)then the ratio (I_(1))/(I_(2)) is ....... |
|
Answer» Solution :For coherent source in `I_(1)=I_(0)"cos^(2){(k(r_(2)-r_(1)))/(2)},r_(2)=r_(1)` `:.I_(1)=I_(0)cos^(2){k((0)/(2))}` `=I_(0)cos^(2)(0)` `I_(1)=I_(0)` but `I_(0)=4I` MAXIMUM intensity and `I=I_(0)or I_(2)` is the intensity of one source. For incoherentsource, `I_(2)=I.+I.+2sqrt(I.I) lt cos delta gt ` `=2I.+2I(0)[ :.` one one PERIOD `lt cos delta gt=0]` `I_(2)=2I.` `:. (I_(1))/(I_(2))=(4I)/(2I)` `:.(I_(1))/(I_(2))=2` |
|
| 2383. |
The circuit shows a resistance, R=0.01Omega and inductance L=3mH connected toa conducting rod PQ of length l=wm which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuitt ois seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity omega2 rad//sec. Find the magnitude of this torque (inN-m) at t=(0.3In 2) second. |
|
Answer» |
|
| 2384. |
The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to |
|
Answer» `d//R^(2)` `=G.(4)/(3)(PIR^(3).d)/(R^(2))=(4 piG)/(3).d.R" or "g prop dR` |
|
| 2385. |
Compare LC oscillations and a force damped oscillations in mechanics. |
|
Answer» Solution :The equation of forced damped oscillations is, `(d^(2)x)/( dt^(2)) + ( b)/( m ) ( DX)/( dx) + ( K )/( m ) x= (F_(0) )/( m)cos omegat`and equation of LCoscillation, `(d^(2)q)/( dt^(2))+( R )/( L ) (dq)/( dt)+ = ( V_(m))/( L ) sin omega t ` `{:("Forced oscillations","Driven LCR circuit"),(m(d^(2)x)/(dt^(2))+b(dx)/(dt) kx = F cos omega_(d)t,L(d^(2)q)/(dt^(2)) + R (dq)/( dt) + (q)/(C ) = V_(m) sin omega t ),("Displacement x ","Charge on capacitor q"),("Time t","Time t"),("Mass m","SELF inductance L"),("Damping constant b","Resistance R"),("Spring constant K","Inverse capacitance "1//C),("Driving frequency" omega_(d),"Driving frequency " omega),("Natural frequency of oscillations"omega,"Natural frequency of LCR circuit " omega_(0)),("AMPLITUDE of forced oscillations A","Maximum charge stored "q_(m)),("Amplitude of driving force "F_(0),"Amplitude of applied voltage"v_(m)):}` |
|
| 2386. |
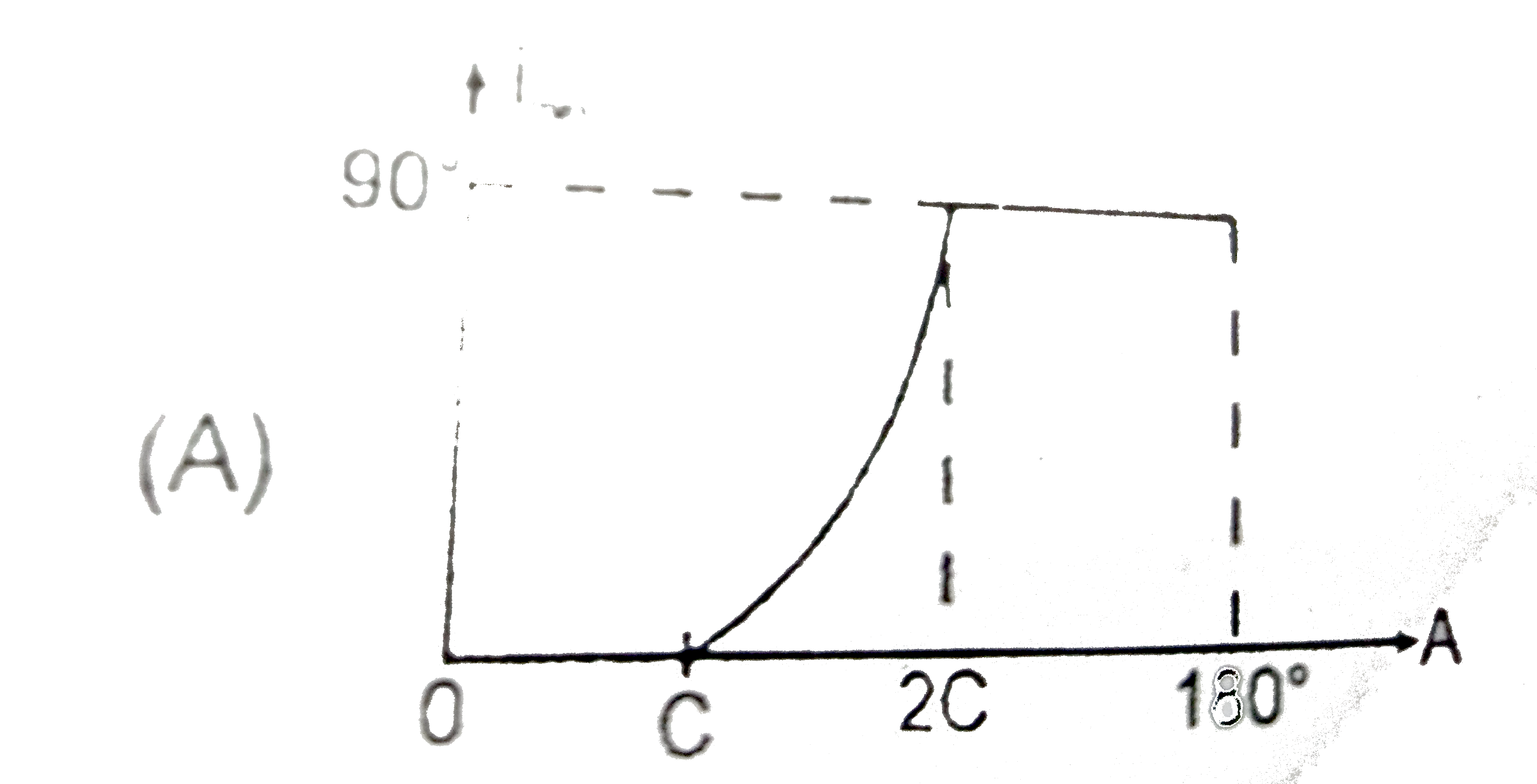
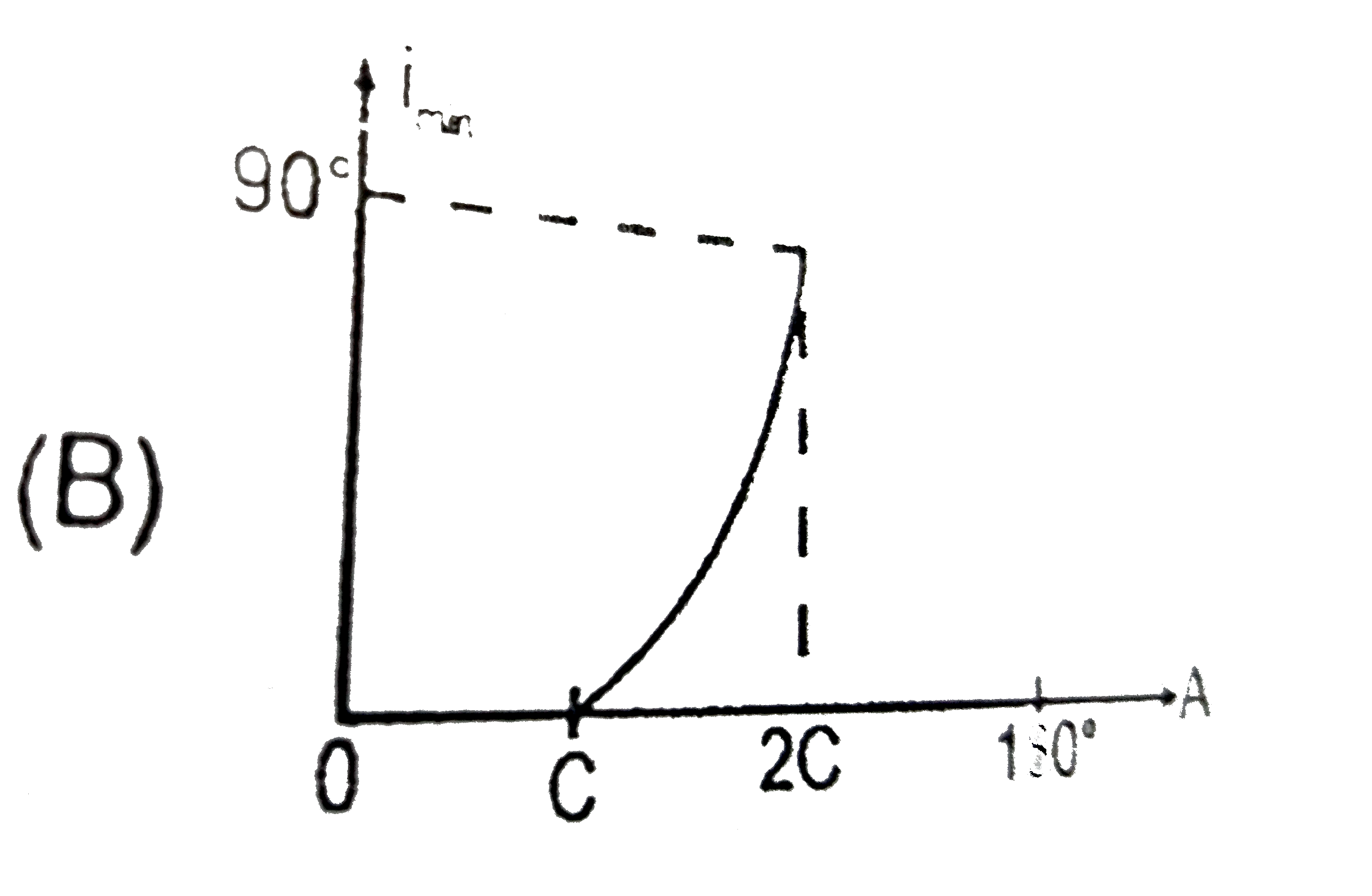
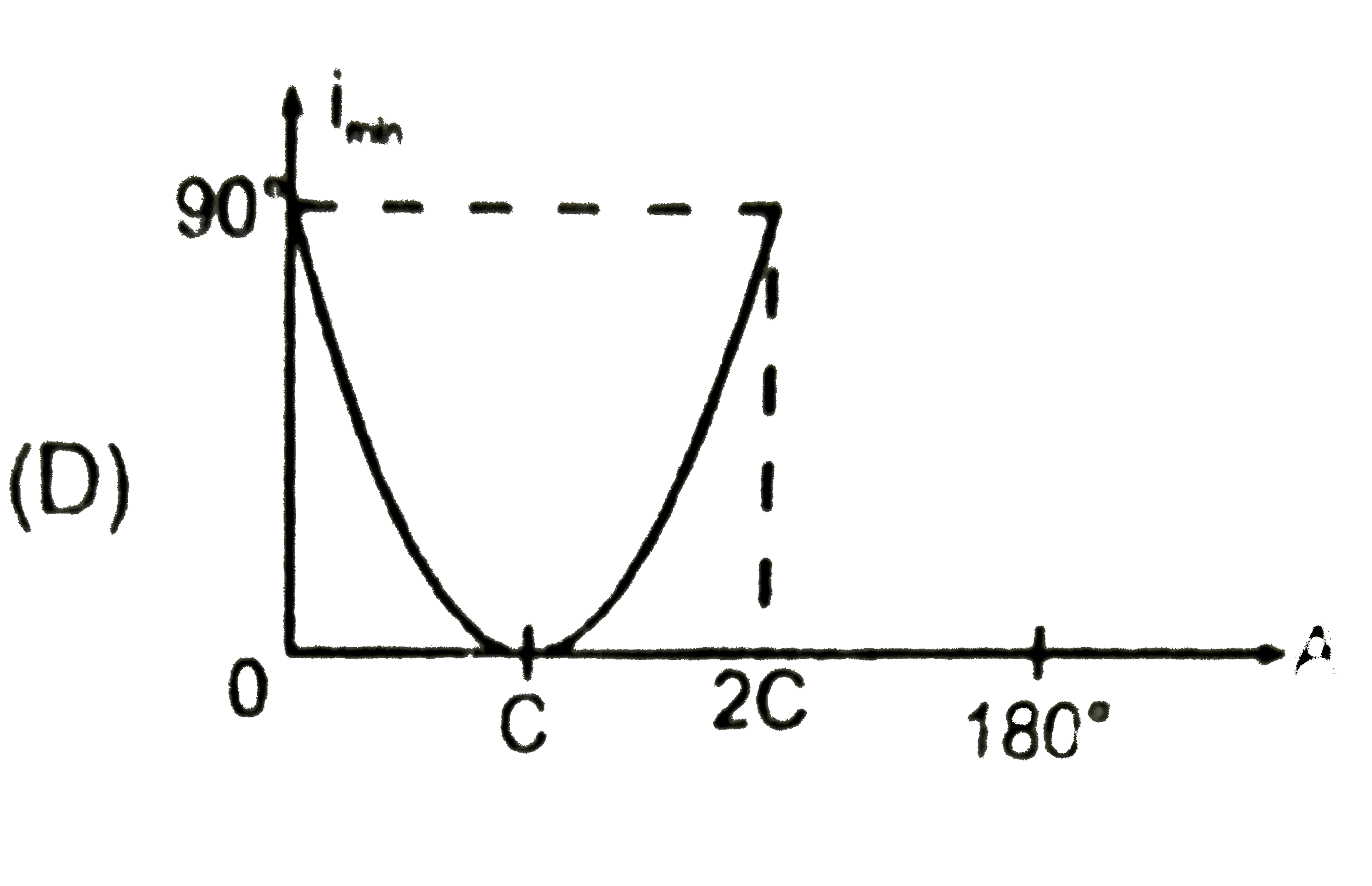
Choose the most appropriate graph of i_(min)v//s A, for a light ray which is incident on one face of a prism and is coming out from the opposite face (without TIR). (The symbols have their standard meanings). |
|
Answer»
|
|
| 2387. |
What is stationary orbit ? |
| Answer» SOLUTION :Bohr POSTULATED that electrons can revolve only around nucleusn in certain discrete non radiating ORBITS in which ANGULAR momentum of electrons is an integral multiple of `H/(2pi)`. | |
| 2388. |
A neutron collides with a stationary He + atom in its ground state, What should be minimum value of energy of neutron (in eV), so that all type of collisions (Elastic, inelastic and perfectly inelastic) can take place ? (Consider mass of He + atom is 4 times mass of neutron). |
|
Answer» `underset("EnergE")underset(to) (m) underset(**)(4m) underset(toV )underset(m+4m)("Perfectly inelstic collision")` `m u + 0= 5mV` `LOSS =1/2 m u ^(2) -1/2 5M xx((4)/(5)) ^(2) =(4E)/(5)` `(4E)/(5) =12.09 xx(2) ^(2) eV` `IMPLIES E =60 . 45 eV` |
|
| 2389. |
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the disc coincide. The centre of mass of the new disc is alphaR from the centre of the bigger disc. The value of alpha is : |
|
Answer» `(1)/(2)`  MASS of bigger disc `M=pi(2R)^(2).t.rho=4piR^(2)trho` Mass of smaller disc `m=piR^(2)trho=piR^(2)trho=(M)/(4)` Mass of remaining portion = `M-m` `=M-(M)/(4)=(3)/(4)M` Let G be the centre of mass of remaining portion and OG be its distance from the centre of mass of the bigger disc. Then taking moments about .O., we get `(3)/(4)MxxOG=(M)/(4)xxO.O` or `(3)/(4)OG=(R)/(4)orOG=(R)/(3)` `ALPHA.R=(R )/(3)` or `alpha=(1)/(3)` |
|
| 2390. |
What is the energy of a photon whose wavelength is 6840A^@ : |
|
Answer» `1.81e V` |
|
| 2391. |
What is absorption spectrum ? |
| Answer» SOLUTION :These are produced by SUBSTANCE light is CALLED absorption SPECTRUM. | |
| 2392. |
Consider a particle moving in the x-y plane according to r=r (cos omegat hat(i)+sin omega t hat(j)), where r and omega are constants. Find the trajectory, the velocity, and the acceleration. |
|
Answer» PERPENDICULAR to the velocity |
|
| 2393. |
In the ground state of .......... electrons are in stable equilibrium, while in ........ electrons always experience a net force. (Thomson's model/ Rutherford's model.) |
| Answer» SOLUTION :Thomson.s MODEL, Rutherford.s model | |
| 2394. |
A mass m is suspendedto a spring of length Land force constant k. The frequency of vibration isv. The spring is cut into two equal parts and each half is loaded with same mass m. The new frequency v' is given by : |
|
Answer» `v'=SQRT(2)v` `:.""v.=(1)/(2pi)sqrt((k.)/(m))` `:.""(v.)/(v)=sqrt(2)IMPLIES""v.=sqrt(2)v` Thus correct choice is (a). |
|
| 2395. |
A current carrying coil is freely suspended in a uniform magnetic field. The coil tends to set its plane ______ . |
|
Answer» Parallel to the magnetic field  `IMPLIES tau` is MAXIMUM when `alpha= 90^(@)` i.e., when the plane of the coil is parallel to the magnetic field `implies tau =0` when `alpha`=0 i.e., when the plane of the coil is perpendicular to the magnetic field Hence the couple SETS the coil in a position in which its plane is perpendicular to themagnetic field. It is the position of stable equilibrium of the coil. |
|
| 2396. |
(a) In Illustration 2.20, how many dark rings will be observed on the wall? (b) What is the Path difference at point P? |
|
Answer» Solution :(a) Path DIFFERENCE corresponding to minima in our given range is `lambda//2, 3 lambda//2, 5 lambda//2`. Hence, three dark rings will be observed on the wall. (b) Path difference between the waves reaching at P, from Fig. 2.20 `Delta x = S_(2) A` `S_(2) P - S_(1) P = Delta x or d cos theta = Delta x` `cos theta = (Delta x)/(d)` But `TAN theta = (y)/(D)` `IMPLIES cos theta = (sqrt(D ^(2) - Y^(2)))/(D)` `(D sqrt(1 - (y^(2))/(D^(2))))/(D)` `= (1 - (y^(2))/(D^(2)))^(1//2) = (1 - (Y^(2))/(2D^(2)))` From (i) `Delta x = d cos theta = d (1-(y^(2))/(2D^(2)))` From (i) and (ii), we can find the RADIUS of any dark of bright ring. |
|
| 2397. |
The dimensional formula of effective torsional constant of spring is _______ . |
|
Answer» `M^(1)L^(2)T^(-3)` |
|
| 2399. |
In electron microscope…….property of electron is used. |
|
Answer» particle |
|
| 2400. |
(a) With the help of a suitable ray diagram, derive the mirror formula for a concave mirror. |
|
Answer» Solution :Mirror Formula for Concave Mirror : LET, AB be the length of an object placed beyond C in front of a concave mirror. The image A 'B' is REAL, inverted and between C and F. Applying sign conventions, we have object distance `PB=-u`, image distance `PB'=-v`, focal length `PF=-f` and radius of curvature `PC=-2f`. In similar `Delta s` ABC and A' B' F `(AB)/(A'B')=(BC)/(B'C)` ...(i) and in similar `Delta s` RSF and A' B' F `(RS)/(A'B')=(SF)/(B'F)"":' ""RS=AB` `(AB)/(A'B')=(SF)/(B'F)` ...(ii) From eq. (i) and (ii), we have `(BC)/(B'C)=(SF)/(B'F)` Since, the aperture of the concave mirror is small so the point S and P coincides. `:. (BC)/(B'C)=(PF)/(B'F)` `(PB-PC)/(PC-PB')=(PF)/(PB'-PE)` `(-u+2f)/(-2f+v)=(-f)/(-v+f)` `UV-uf-2vf+2f^(2)=2f^(2)-fv` `implies uv=uf+vf` Dividing both sides by `uvf`, we get `(uv)/(uvf)=(uf)/(uvf)+(vf)/(uvf)"":.""1/f=1/v+1/u`. 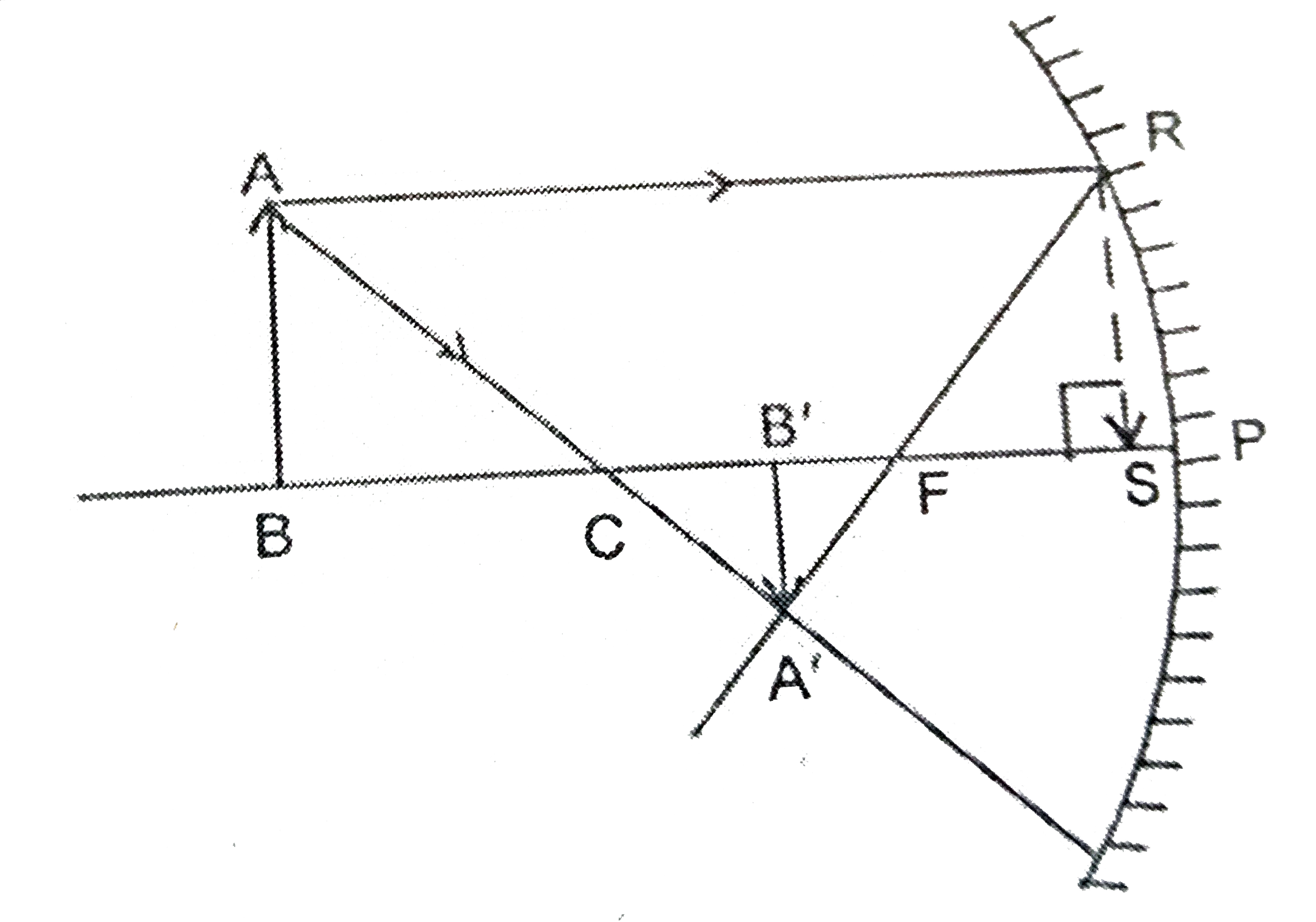
|
|
 `
`